Лекции и примеры решения задач механики. Что такое модуль упругости
Модуль упругости - что это такое? Определение модуля упругости для материалов
Модуль упругости - это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов

Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Модуль Юнга в действии
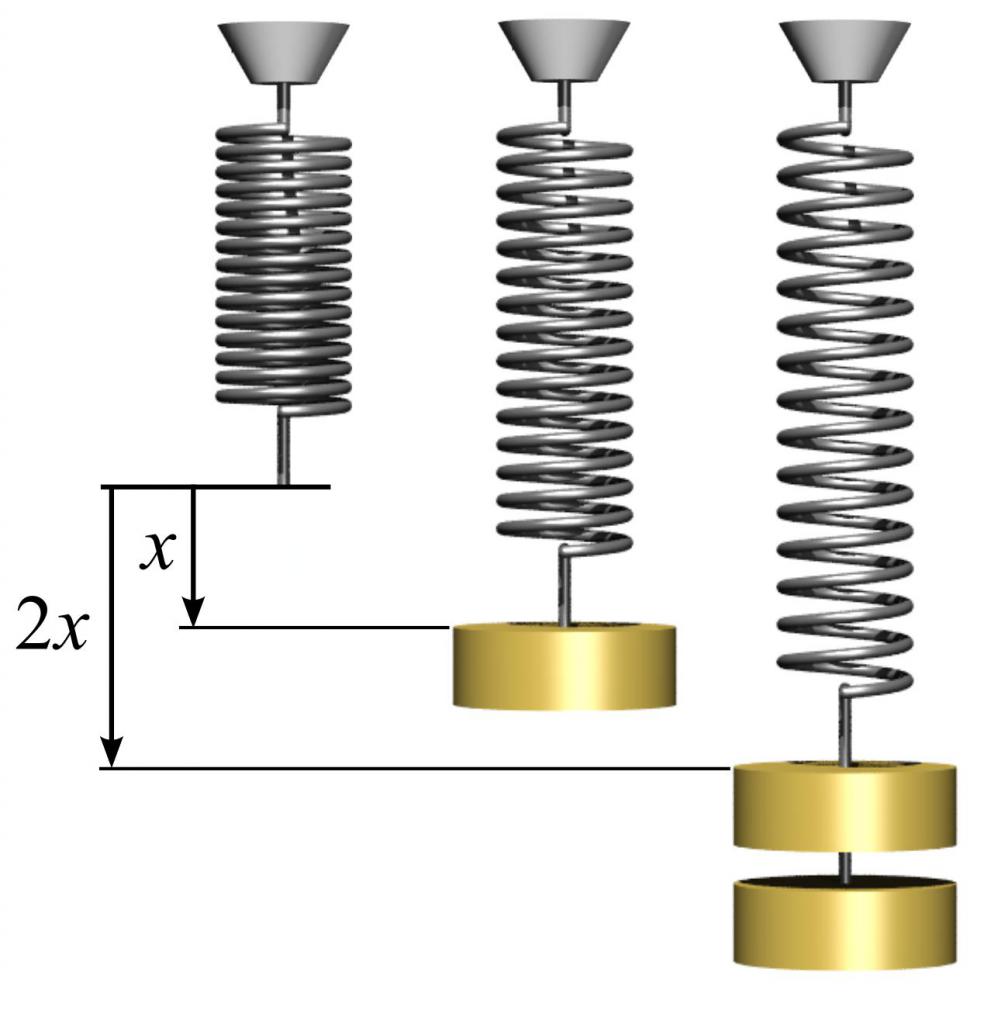
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п - число пи, равное 3,14, а r - радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g - ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d - относительная деформация в упругой области.
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия - явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Модуль сдвига
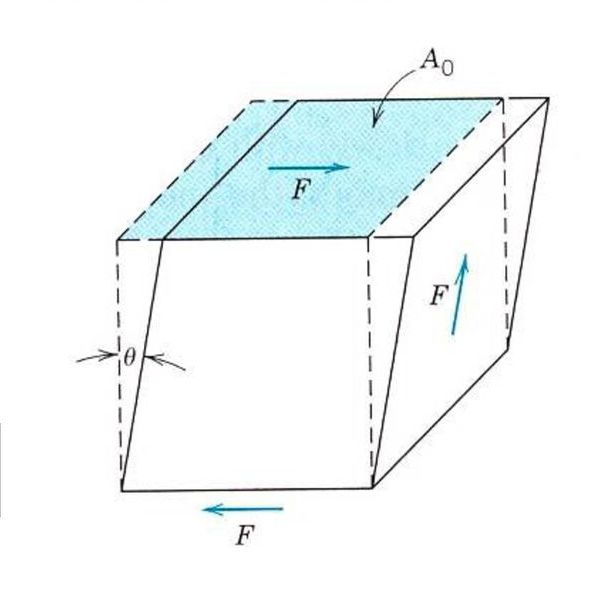
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Модуль упругости дерева

Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.

Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
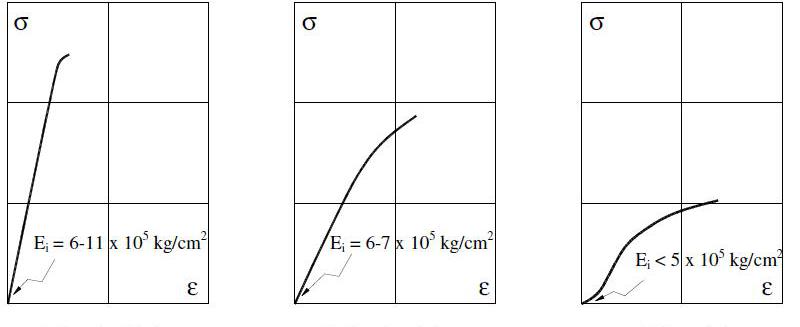
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
fb.ru
Модуль упругости стали в кгс\см2, примеры
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Значение модуля упругости
Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.
Некоторые упруго - пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.
Вот примеры значений модуля Юнга (в миллионах кгс\см2) некоторых материалов:
- Чугун белый – 1,15.
- Чугун серый -1,16.
- Латунь – 1,01.
- Бронза - 1,00.
- Кирпичная каменная кладка – 0,03.
- Гранитная каменная кладка – 0,09.
- Бетон – 0,02.
- Древесина вдоль волокон – 0,1.
- Древесина поперек волокон – 0,005.
- Алюминий – 0,7.
Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:
- Стали конструкционные высокого качества (20, 45) – 2,01.
- Стали обычного качества (Ст.3, Ст.6) - 2,00.
- Стали низколегированные (30ХГСА, 40Х) – 2,05.
- Стали нержавеющие (12Х18Н10Т) – 2,1.
- Стали штамповые (9ХМФ) – 2,03.
- Стали пружинные (60С2) – 2,03.
- Стали подшипниковые (ШХ15) – 2,1.
Также значение модуля упругости для сталей изменяется исходя из вида проката:
- Проволока высокой прочности – 2,1.
- Плетенный канат – 1,9.
- Трос с металлическим сердечником – 1,95.
Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.
Оцените статью:Рейтинг: 0/5 - 0 голосов
prompriem.ru
Модуль Юнга (упругости I рода)
Модуль Юнга (синонимы: модуль упругости I рода, модуль продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой EЕдиница измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.

Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).
E=σ/ε=tgα
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Таблица 1
| Материал | Модуль ЮнгаE, [ГПа] |
| Сталь | 200 |
| Чугун | 120 |
| Серый чугун | 110 |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Титан | 120 |
| Бронза | 100 |
| Латунь | 95 |
| Медь | 110 |
| Олово | 35 |
| Хром | 300 |
| Никель | 210 |
| Кремний | 110 |
| Свинец | 18 |
| Бетон | 20 |
| Дерево | 10 |
| Стекло | 70 |
Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:
σ=Eε
Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:
EA – жесткость поперечного сечения при растяжении-сжатии,где A – площадь поперечного сечения стержня;EI – жесткость поперечного сечения при изгибе,где I – осевой момент инерции сечения балки.
Модуль упругости II рода (модуль сдвига) >Примеры решения задач >
isopromat.ru
Модули упругости - это... Что такое Модули упругости?
величины, характеризующие упругие свойства материала. В случае малых деформаций, когда справедлив Гука закон, т. е. имеет место линейная зависимость между напряжениями и деформациями, М. у. представляют собой коэффициент пропорциональности в этих соотношениях. Одностороннему нормальному напряжению σ, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости Е (модуль Юнга). Он равен отношению нормального напряжения σ к относительному удлинению ε, вызванному этим напряжением в направлении его действия: Е = σ/ ε, и характеризует способность материала сопротивляться растяжению. Напряжённому состоянию чистого сдвига, при котором по двум взаимно перпендикулярным площадкам действуют только касательные напряжения τ, соответствует модуль сдвига G. Модуль сдвига равен отношению касательного напряжения τ к величине угла сдвига γ, определяющего искажение прямого угла между плоскостями, по которым действуют касательные напряжения, т. е. G = τ/γ. Модуль сдвига определяет способность материала сопротивляться изменению формы при сохранении его объёма. Всестороннему нормальному напряжению σ, одинаковому по всем направлениям (возникающему, например, при гидростатическом давлении), соответствует модуль объёмного сжатия K — объёмный модуль упругости. Он равен отношению величины нормального напряжения σ к величине относительного объёмного сжатия Δ, вызванного этим напряжением: K = σ/Δ. Объёмный модуль упругости характеризует способность материала сопротивляться изменению его объёма, не сопровождающемуся изменением формы. К постоянным величинам, характеризующим упругие свойства материала, относится также Пуассона коэффициент ν. Величина его равна отношению абсолютному значения относительного поперечного сжатия сечения ε' (при одностороннем растяжении) к относительному продольному удлинению ε, т. е. ν = |ε'|/ε.В случае однородного изотропного тела М. у. одинаковы по всем направлениям. Четыре постоянные величины Е, G, K и ν связаны между собой двумя соотношениями:
Следовательно, только две из них являются независимыми величинами и упругие свойства изотропного тела определяются двумя упругими постоянными. В случае анизотропного материала постоянные Е, G и ν принимают различные значения в различных направлениях и величины их могут изменяться в широких пределах. Количество М. у. анизотропного материала зависит от структуры материала. Анизотропное тело, лишённое всякой симметрии в отношении упругих свойств, имеет 21 М. у. При наличии симметрии в материале число М. у. сокращается.
М. у. устанавливаются экспериментально-механическим испытанием образцов изучаемых материалов. М. у. не являются строго постоянными величинами для одного и того же материала, их значения меняются в зависимости от химического состава материала, от его предварительной обработки (термическая обработка, прокат, ковка и др.). Значения М. у. также зависят от температуры материала.
Лит.: Фридман Я. Б., Механические свойства металлов, 2 изд., М., 1952.
dic.academic.ru
| Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам: | |||||||||
| (λ,G){\displaystyle (\lambda ,\,G)} | (E,G){\displaystyle (E,\,G)} | (K,λ){\displaystyle (K,\,\lambda )} | (K,G){\displaystyle (K,\,G)} | (λ,ν){\displaystyle (\lambda ,\,\nu )} | (G,ν){\displaystyle (G,\,\nu )} | (E,ν){\displaystyle (E,\,\nu )} | (K,ν){\displaystyle (K,\,\nu )} | (K,E){\displaystyle (K,\,E)} | |
| K={\displaystyle K=}модуль объемной упругости | λ+2G3{\displaystyle \lambda +{\frac {2G}{3}}} | EG3(3G−E){\displaystyle {\frac {EG}{3(3G-E)}}} | λ1+ν3ν{\displaystyle \lambda {\frac {1+\nu }{3\nu }}} | 2G(1+ν)3(1−2ν){\displaystyle {\frac {2G(1+\nu )}{3(1-2\nu )}}} | E3(1−2ν){\displaystyle {\frac {E}{3(1-2\nu )}}} | ||||
| E={\displaystyle E=}модуль продольной упругости Юнга | G3λ+2Gλ+G{\displaystyle G{\frac {3\lambda +2G}{\lambda +G}}} | 9KK−λ3K−λ{\displaystyle 9K{\frac {K-\lambda }{3K-\lambda }}} | 9KG3K+G{\displaystyle {\frac {9KG}{3K+G}}} | λ(1+ν)(1−2ν)ν{\displaystyle {\frac {\lambda (1+\nu )(1-2\nu )}{\nu }}} | 2G(1+ν){\displaystyle 2G(1+\nu )} | 3K(1−2ν){\displaystyle 3K(1-2\nu )} | |||
| λ={\displaystyle \lambda =}первый параметр Ламе | GE−2G3G−E{\displaystyle G{\frac {E-2G}{3G-E}}} | K−2G3{\displaystyle K-{\frac {2G}{3}}} | 2Gν1−2ν{\displaystyle {\frac {2G\nu }{1-2\nu }}} | Eν(1+ν)(1−2ν){\displaystyle {\frac {E\nu }{(1+\nu )(1-2\nu )}}} | 3Kν1+ν{\displaystyle {\frac {3K\nu }{1+\nu }}} | 3K(3K−E)9K−E{\displaystyle {\frac {3K(3K-E)}{9K-E}}} | |||
| G={\displaystyle G=}модуль сдвига или второй параметр Ламе | 3K−λ2{\displaystyle 3{\frac {K-\lambda }{2}}} | λ1−2ν2ν{\displaystyle \lambda {\frac {1-2\nu }{2\nu }}} | E2+2ν{\displaystyle {\frac {E}{2+2\nu }}} | 3K1−2ν2+2ν{\displaystyle 3K{\frac {1-2\nu }{2+2\nu }}} | 3KE9K−E{\displaystyle {\frac {3KE}{9K-E}}} | ||||
| ν={\displaystyle \nu =}коэф. пуассона | λ2(λ+G){\displaystyle {\frac {\lambda }{2(\lambda +G)}}} | E2G−1{\displaystyle {\frac {E}{2G}}-1} | λ3K−λ{\displaystyle {\frac {\lambda }{3K-\lambda }}} | 3K−2G2(3K+G){\displaystyle {\frac {3K-2G}{2(3K+G)}}} | 3K−E6K{\displaystyle {\frac {3K-E}{6K}}} | ||||
| M={\displaystyle M=} | λ+2G{\displaystyle \lambda +2G} | G4G−E3G−E{\displaystyle G{\frac {4G-E}{3G-E}}} | 3K−2λ{\displaystyle 3K-2\lambda } | K+4G3{\displaystyle K+{\frac {4G}{3}}} | λ1−νν{\displaystyle \lambda {\frac {1-\nu }{\nu }}} | G2−2ν1−2ν{\displaystyle G{\frac {2-2\nu }{1-2\nu }}} | E1−ν(1+ν)(1−2ν){\displaystyle E{\frac {1-\nu }{(1+\nu )(1-2\nu )}}} | 3K1−ν1+ν{\displaystyle 3K{\frac {1-\nu }{1+\nu }}} | 3K3K+E9K−E{\displaystyle 3K{\frac {3K+E}{9K-E}}} |
ru-wiki.org
модуль упругости - это... Что такое модуль упругости?
модуль упругости3.8 модуль упругости: Параметр, определяемый величиной деформации под воздействием нагружения, используется для характеристики прочности дорожных одежд.
Модуль упругости
Е
Характеристика сопротивления материала деформации при растяжении или сжатии, численно равная отношению напряжения, возникающего при растяжении или сжатии, к соответствующей ему упругой деформации, кгс/см2
Смотри также родственные термины:
18. Модуль упругости (начальный)
Eн
Отношение приращения напряжения к соответствующему приращению упругой деформации на начальном этапе нагружения
Модуль упругости бетона
Еs
Коэффициент пропорциональности между нормальным напряжением и соответствующей ему относительной продольной упругомгновенной деформацией при s1 = 0,3Rпр при осевом сжатии образца
Модуль упругости Е
Отношение приращения напряжения к соответствующему приращению удлинения в пределах упругой деформации
2. Модуль упругости нагретого до 200-300° бетона в зависимости от проектной марки бетона на сжатие приведен в табл. 2.
Таблица 2
Значения Eσt10-4, Мн/м2
| Бетон | Проектная марка бетона | |||||||
| М100 | M200 | М300 | М400 | М500 | М600 | М700 | М800 | |
| Тяжелый | 1 | 1,4 | 1,7 | 2 | 2,2 | 2,3 | 2,3 | 2,4 |
| На пористых заполнителях с плотностью, кг/м3: | ||||||||
| 1,4 | 0,6 | 0,7 | 0,8 | - | - | - | - | - |
| 1,8 | 0,7 | 0,9 | 1,1 | 1,2 | - | - | - | - |
| 2,2 | - | 1,1 | 1,3 | 1,4 | - | - | - | - |
Примечание. Для бетона тепловлажностной обработки при атмосферном давлении значения Еσtумножаются на 0,9, а для бетона автоклавной обработки - на 0,77.
3.4 модуль упругости при сжатии (compression modulus of elasticity) E: Отношение напряжения сжатия к соответствующей относительной деформации образца при условии, что зависимость между этими характеристиками является прямо пропорциональной (см. рисунок 1).
3.4 модуль упругости при сжатии (compression modulus of elasticity) E: Отношение напряжения сжатия к соответствующей относительной деформации образца при условии, что зависимость между этими характеристиками является прямо пропорциональной (см. рисунок 1).

Fp - сила, соответствующая предварительной нагрузке; Fm - максимальная сила;
Рисунок 1 - Примеры графиков зависимости деформации образца от прилагаемой силы
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- модуль управления
- Модуль упругости (начальный)
Смотреть что такое "модуль упругости" в других словарях:
Модуль упругости — Модуль упругости общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль… … Википедия
Модуль упругости — – коэффициент пропорциональности между приложенным к телу напряжением (в упругой области) и обусловленной им величиной деформации. [Тарасов В. В. Материаловедение. Технология конструкционных материалов: учебное пособие для вузов / В. В.… … Энциклопедия терминов, определений и пояснений строительных материалов
модуль упругости — Модуль 2., характеризующий сопротивление материала упругой деформации [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] модуль упругости Отношение силы растяжения, приходящейся на единицу площади поперечного сечения … Справочник технического переводчика
МОДУЛЬ УПРУГОСТИ — (Modulus of elasticity) см. Юнга модуль. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
МОДУЛЬ УПРУГОСТИ — числовая величина, характеризующая зависимость между напряжением материала и его упругой деформацией. Указанная зависимость определяется законом Гука, устанавливающим, что напряжение равно М. у., умноженному на относительное удлинение (или… … Технический железнодорожный словарь
Модуль упругости Е — Отношение приращения напряжения к соответствующему приращению удлинения в пределах упругой деформации Источник: ГОСТ 1497 84: Металлы. Методы испытаний на растяжение оригинал документа … Словарь-справочник терминов нормативно-технической документации
модуль упругости — [modulus of elasticity] величина, характеризующая упругие свойства материала. В случае малых деформаций, когда справедлив закон Гука, т.е. имеет место линейная зависимость между напряжениями и деформациями, модуль упругости представляет… … Энциклопедический словарь по металлургии
Модуль упругости (Е) — Modulus of elasticity Модуль упругости (Е). (1) Критерий жесткости материала; отношение напряжения вне предела пропорциональности к соответствующему напряжению. Если растягивающее напряжение 13,8 МПа приводит к удлинению на 1,0 %, модуль… … Словарь металлургических терминов
модуль упругости — tampros modulis statusas T sritis chemija apibrėžtis Įtempio ir santykinės deformacijos santykis. atitikmenys: angl. Young modulus; modulus of elasticity rus. модуль упругости; модуль Юнга ryšiai: sinonimas – Jungo modulis … Chemijos terminų aiškinamasis žodynas
модуль упругости — tampros modulis statusas T sritis fizika atitikmenys: angl. modulus of elasticity vok. Elastizitätsmodul, m rus. модуль упругости, m pranc. module d’élasticité, m … Fizikos terminų žodynas
normative_reference_dictionary.academic.ru
Модуль Упругости — Все формулы
Модуль Упругости — коэффициент, характеризующий сопротивление материала растяжению или сжатию при упругой деформации
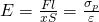
С помощью легких преобразований, данная формула получается из Закона Гука.
Модуль Упругости , или модуль продольной деформации Е показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения.
Таблица значений Модуля Юнга (Модуля Упругости) для некоторых материалов
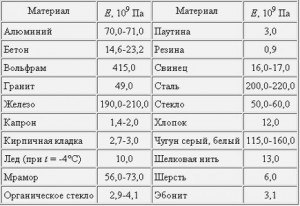
Физический смысл Модуля Юнга : он показывает напряжение, которое необходимо приложить к телу, чтобы удлинить его в два раза
В формуле мы использовали :
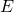 — Модуль упругости (Модуль Юнга)
— Модуль упругости (Модуль Юнга)
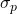 — Критическое напряжение
— Критическое напряжение
 — Относительное удлинение
— Относительное удлинение
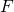 — Сила, действующая на стержень
— Сила, действующая на стержень
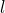 — Длина деформируемого стержня
— Длина деформируемого стержня
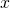 — Модуль изменения длины стержня в результате упругой деформации
— Модуль изменения длины стержня в результате упругой деформации
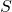 — Площадь поверхности, по которой распределено действие силы
— Площадь поверхности, по которой распределено действие силы
xn--b1agsdjmeuf9e.xn--p1ai










