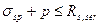Объем кольца онлайн калькулятор. Площадь кольца. Расчет кольца площади
Формула площади кольца
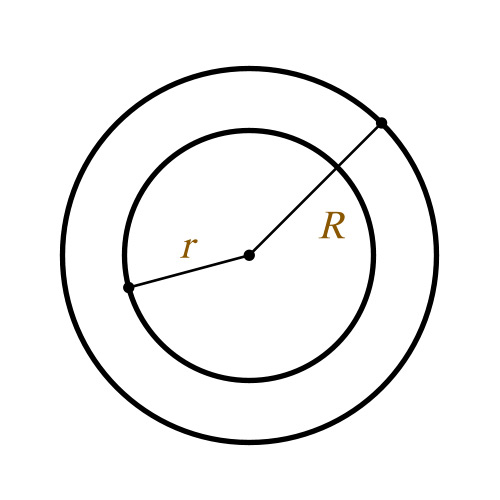
Кольцо, это геометрическая фигура, которая имеет внешний радиус R и внутренний радиус r с общим центром. В повседневной жизни с кольцами приходится встречаться не так уж и редко, поскольку они являются необходимыми элементами многих технических устройств, которыми пользуются практически все. Еще чаще с кольцами имеют дело инженеры и конструкторы, создающие всевозможные машины, узлы и агрегаты.
Расчет площади кольца
Найти площадь кольца можно по формуле:
S = π ( R2− r2)
R – радиус внешней окружности
r – радиус внутренней окружности
S – площадь кольца
π – 3.14
Форму колец имеют шайбы, являющимися элементами крепежа, которые устанавливаются между головками болтов или гаек и скрепляемых изделий для того, чтобы увеличить площадь прилегания, а также для того, чтобы предотвратить самопроизвольное отвинчивание. Если требуется в том или ином случае рассчитать или подобрать для установки в изделие именно ту шайбу, которая необходима, конструкторам нужно, помимо всего прочего, найти площадь кольца. Эти детали чаще всего изготавливаются из стали, цветных металлов или пластмасс и могут иметь как плоскую, так и специальную поверхность. Во втором случае шайбы производятся из пружиненной стали, называемые гроверными шайбами которые служат для предотвращения ослабления резьбовых соединений при тряске и вибрациях.
Большое распространение в технике получили также и уплотнительные кольца. Они предназначаются для того, чтобы обеспечить герметизацию соединений в трубопроводах, по которым производится транспортировка газов или жидкостей, а также в пневматических и гидравлических агрегатах. Устанавливаются они в местах соединений различных деталей и благодаря своей эластичности очень плотно прилегают к поверхностям, между которыми располагаются. Наиболее распространенным материалом для изготовления уплотнительных колец является резина различных сортов и составов, а также некоторые специальные виды пластических масс.
Практически все современные двигатели внутреннего сгорания имеют в своей конструкции такие важные элементы, как поршневые кольца. Эти детали нужны для того, чтобы достичь необходимой степени компрессии в камере сгорания и располагаются между поршнями и стенками цилиндров. Поскольку при работе силовых агрегатов они испытывают постоянное трение, то со временем изнашиваются и требуют замены. Изготавливаются поршневые кольца чаще всего из высококачественного серого чугуна.
Еще одной разновидностью колец являются стопорные кольца. Они используются для фиксации различных механических деталей и почти всегда устанавливаются в специально проточенных для них канавках. Чаще всего стопорные кольца можно встретить на валах, однако нередко они располагаются и в корпусах деталей. В зависимости от местонахождения они подразделяются на те, которые предназначены для вала и те, которые монтируются в отверстиях, а что касается материала изготовления этих деталей, то им чаще всего является сталь. После установки на свое «законное» место стопорное кольцо обычно немного разжимается и своими торцевыми поверхностями препятствует смещению деталей друг относительно друга.
определить площадь кольца, если известны радиусы
Условие задачи:
Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.
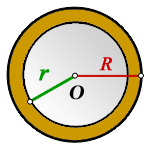
Дано:Радиус внешней окружности, R = 10 смРадиус внутренней окружности, r = 8 см
Пояснение к рисунку:O - общий центр окружностей
Найти площадь кольца: S
Решение
Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.
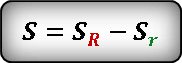
Формула площади внешнего круга.
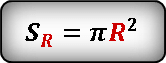
Формула площади внутреннего круга.
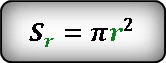
После подстановки и преобразования, получаем следующее выражение для площади кольца.
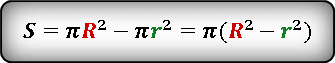
Вставляем значения.
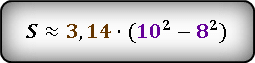
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета площади кольца
www-formula.ru
Объем кольца онлайн калькулятор. Площадь кольца
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус.
Площадь кольца, выраженная через внешний и внутренний радиусы
Пусть дана окружность радиуса R и окружности радиуса r . Причем R>r . Совместим центры этих окружностей. Фигура, заключенная между этими окружностями и будет кольцо, у которого R является внешним радиусом, r -внутренним радиусом.Тогда площадь этой фигуры будет равна разницы между с большим радиусом и площадью круга с меньшим радиусом.
Площадь круга с радиусом r выражается формулой:Площадь круга с радиусом R выражается формулой:
Тогда площадь кольца будет равна:
Таким образом, площадь кольца равна произведению числа на разницу квадратов внешнего и внутреннего радиусов:
Пример расчета площади кольца, если известны его радиусы.Найдите площадь кольца, если его внешний радиус равен 3, а внутренний – 2
Площадь кольца, выраженная через внешний и внутренний диаметры
Иногда при решении задач удобней использовать формулу площади кольца, выраженную через внутренний и внешний диаметры.
Пусть D — внешний диаметр кольца, d -внутренний диаметр кольца, тогда:Выразим радиус через диаметр. Имеем:Площадь кольца вычисляется по формуле:Подставив выраженные через диаметр радиусы, получим:Таким образом, площадь кольца равна четверти произведения числа на разницу квадратов внешнего и внутреннего диаметров:
Пример расчета площади кольца, если известны его диаметры.Найдите площадь кольца, если его внешний диаметр равен 10, а внутренний – 6Площадь кольца вычисляется по формуле:Подставив значения из условия задачи, имеем:
Площади кольца, выраженная через средний радиус и ширину кольца
Пусть k — ширина кольца, являющийся разницей между большим и меньшим радиусом, то есть k=R-r -средний радиус кольца, равный Площадь кольца вычисляется по формуле:Применив формулу разности квадратов, имеем:
Но R-r=k, а Подставим правые части равенства в формулу площади кольца.Получим:
Площадь кольца равна удвоенному произведению числа среднего радиуса на ширину кольца.
Кольцо , это геометрическая фигура, которая имеет внешний радиус R и внутренний радиус r с общим центром. В повседневной жизни с кольцами приходится встречаться не так уж и редко, поскольку они являются необходимыми элементами многих технических устройств, которыми пользуются практически все. Еще чаще с кольцами имеют дело инженеры и конструкторы, создающие всевозможные машины, узлы и агрегаты.
Расчет площади кольца
Найти площадь кольца можно по формуле:
S = π (R 2 − r 2)
R - радиус внешней окружности
r - радиус внутренней окружности
S - площадь кольца
π - 3.14
Форму колец имеют шайбы, являющимися элементами крепежа, которые устанавливаются между головками болтов или гаек и скрепляемых изделий для того, чтобы увеличить площадь прилегания, а также для того, чтобы предотвратить самопроизвольное отвинчивание. Если требуется в том или ином случае рассчитать или подобрать для установки в изделие именно ту шайбу, которая необходима, конструкторам нужно, помимо всего прочего, найти площадь кольца . Эти детали чаще всего изготавливаются из стали, цветных металлов или пластмасс и могут иметь как плоскую, так и специальную поверхность. Во втором случае шайбы производятся из пружиненной стали, называемые гроверными шайбами которые служат для предотвращения ослабления резьбовых соединений при тряске и вибрациях.
Большое распространение в технике получили также и уплотнительные кольца . Они предназначаются для того, чтобы обеспечить герметизацию соединений в трубопроводах, по которым производится транспортировка газов или жидкостей, а также в пневма
territorygarden.ru
Калькулятор расчета характеристик кольцевого сечения (трубы)
- ГЛАВНАЯ
- расчеты
- мониторинг
- консалтинг
- ОБЪЕКТЫ
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
- ОНЛАЙН
- сосуды и аппараты
- трубопроводы
- прочие
- математика
- МАТЕРИАЛЫ
- статьи
- презентации
- log-files
- прочие
- ЛИТЕРАТУРА
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
- Карта сайта
Искать...
cae-cube.ru
