Пропорция (математика). Пропорция для

Пропорция масла и бензина: онлайн Калькулятор

JavaScript отключен в вашем веб-браузере. Для полной функциональности этого сайта необходимо включить JavaScript.

Рассчитать

Результат расчета топливной смеси:

Пропорция масла

Таблица 1. Пропорция 1:50 для объема бензина 1,75 литров.

Пропорция Соотношение смеси Бензин, [литры] Масло, [миллилитры]

Таблица 2. Пропорция 1:50 бензин/масло.

Пропорция Соотношение смеси Бензин, [литры] Масло, [миллилитры]

Формула расчета: 1:50 > 1л/50*1000=20мл. > На литр бензина нужно 20мл масла.

Чтобы удобнее отмерять нужный объем масла в миллилитрах воспользуйтесь медицинским шприцом большего объема, он стоит недорого, продается в любой аптеке. Или используйте любую мерную емкость с делениями. Наш калькулятор поможет вам сосчитать нужную пропорцию для заправки любого бензоинструмента, например: лодочного мотора, бензопилы, триммера, газонокосилки и т.д. Иными словами вы сможете самостоятельно и бесплатно рассчитать правильное соотношение бензина и масла для двухтактных двигателей. Инструкция по смешиванию на фото ниже. Как разбавить бензин с маслом

Важно, перед началом расчета ознакомьтесь с инструкцией по эксплуатации инструмента, в частности с пунктами: заправочные объемы, соотношение топливной смеси. Эти данные будут исходными для правильного расчета.

Для вашего удобства получившийся результат можно распечатать на принтере, нажав значок «На печать». Будим рады конструктивным комментариям и отзывам касаемо работы нашего сервиса.

Как смешать бензин и масло?

Учтите, что у бензоинструмента существует период обкатки и соотношение бензин/масло отличается от рекомендованного.

villadacha.ru

Решение пропорций | Математика

Рассмотрим решение пропорций на конкретных примерах.

Решить уравнения с пропорцией:

1) 25 : x = 10 : 18

Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:

$x = \frac{{\mathop {25}\limits^5 \cdot \mathop {18}\limits^9 }}{{\mathop {10}\limits_{\mathop 2\limits_1 } }}$

25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.

$x = 45$

Ответ: 45.

$2)\frac{y}{{21}} = \frac{9}{{14}}$

Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:

$y = \frac{{\mathop {21}\limits^3 \cdot 9}}{{\mathop {14}\limits_2 }}$

$y = \frac{{27}}{2}$

$y = 13,5$

Ответ: 13,5.

При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.

$3)4,5:0,6 = z:2,4$

Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:

$z = \frac{{4,5 \cdot 2,4}}{{0,6}}$

В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:

$z = \frac{{4,5 \cdot 10 \cdot 2,4 \cdot 10}}{{0,6 \cdot 100}}$

Сокращаем 24 и 6 на 6, 10 и 45 — на 5:

$z = \frac{{\mathop {45}\limits^9 \cdot \mathop {24}\limits^4 }}{{\mathop 6\limits_1 \cdot \mathop {10}\limits_2 }}$

Еще раз сокращаем 4 и 2 на 2:

$z = \frac{{9 \cdot \mathop 4\limits^2 }}{{\mathop 2\limits_1 }}$

$z = 18$

Ответ: 18.

Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.

$4)k:2\frac{3}{{23}} = 3\frac{2}{7}:\frac{1}{4}$

Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:

$k = 2\frac{3}{{23}} \cdot 3\frac{2}{7}:\frac{1}{4}$

Смешанные числа переводим в неправильные дроби:

$k = \frac{{49}}{{23}} \cdot \frac{{23}}{7} \cdot 4$

$k = \frac{{\mathop {49}\limits^7 \cdot \mathop {23}\limits^1 \cdot 4}}{{\mathop {23}\limits_1 \cdot \mathop 7\limits_1 }}$

$k = 28$

Ответ: 28.

При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.

$5)\frac{{2x - 3}}{{15}} = \frac{6}{5}$

Произведение крайних членов пропорции равно произведению средних членов:

$5(2x - 3) = 15 \cdot 6$

Здесь удобно упростить уравнение, разделив обе части на 5:

$2x - 3 = 3 \cdot 6$

$2x - 3 = 18$

$2x = 18 + 3$

$2x = 21$

$x = 21:2$

$x = 10,5$

Ответ: 10,5.

$6)\frac{{2x - 3,2}}{{1,2}} = \frac{{5x - 6}}{{0,5}}$

Произведение крайних членов пропорции равно произведению ее средних членов:

$1,2(5x - 6) = 0,5(2x - 3,2)$

Для упрощения вычислений удобно умножить каждую часть уравнения на 10:

$1,2(5x - 6) = 0,5(2x - 3,2)\_\_\_\left| { \cdot 10} \right.$

$12(5x - 6) = 5(2x - 3,2)$

$60x - 72 = 10x - 16$

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

$60x - 10x = - 16 + 72$

$50x = 56$

Обе части уравнения делим на число, стоящее перед иксом:

$x = 56:50$

$x = 1,12$

Ответ: 1,12.

www.for6cl.uznateshe.ru

Пропорции - это... Что такое Пропорции?

пропорции — 3.41 пропорции: Соотношение геометрических параметров бриллианта, определяемых отношением размеров его основных элементов к среднему диаметру или ширине (для бриллиантов фантазийных форм), выраженное в процентах или числовым значением.… … Словарь-справочник терминов нормативно-технической документации

ПРОПОРЦИИ — (от лат. proportio соотношение, соразмерность) в архитектуре соразмерность элементов, система отношений частей здания, сооружения и т. п. между собой и с целым, придающие ему гармонич. целостность и художеств. завершённость. П. возникают как… … Большой энциклопедический политехнический словарь

Пропорции — (от лат. proportio соотношение, соразмерность) термин худож. практики, к рым определяется соотношение величин эл тов худож. произв., а также отд. эл тов и всего произв. в целом. Понятие П. применяется как к изображению, так и к натуре. Различают… … Российский гуманитарный энциклопедический словарь

Пропорции общественного производства — соотнесение материально вещественных элементов производства и рабочей силы, а также отраслей производства и частей совокупного общественного продукта в процессе воспроизводства. Выделяют следующие пропорции: между сферой материального… … Финансовый словарь

ПРОПОРЦИИ ОБЩЕСТВЕННОГО ПРОИЗВОДСТВА — (от лат. proportio соотношение, соразмерность) англ. proportions of public/social production; нем. Proportionen der gesellschaftlichen Produktion. Соотнесение материально вещественных элементов производства и рабочей силы, а также отраслей… … Энциклопедия социологии

ПРОПОРЦИИ ТЕЛА ЧЕЛОВЕКА — (от лат. proportio соразмерность, соотношение), соотношения размеров отдельных частей тела (туловища, конечностей и их сегментов и др.). Как правило, размеры отд. частей тела рассматриваются в соотношении с ростом (длиной тела) в целом, либо по… … Биологический энциклопедический словарь

пропорции шрифта — (Proportion) Отношение ширины [расстояние от крайней левой до крайней правой точки] и высоты знаков шрифта. Измеряется, как правило, по внешним контурам основных штрихов [доминирующий вертикальный или наклонный штрих] знака «Н». Изменения… … Шрифтовая терминология

пропорции архитектурные — Средство архитектурной композиции, заключающееся в закономерном соотношении размеров архитектурных форм и их частей [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики архитектура, основные понятия EN… … Справочник технического переводчика

пропорции издания — Соотношение размеров ширины высоты и толщины издания, устанавливаемое в зависимости от функциональных особенностей издания и художественного стиля времени. [ГОСТ Р 7.0.3 2006] Тематики издания, основные виды и элементы Обобщающие термины… … Справочник технического переводчика

Пропорции тела — Телосложение размеры, формы, пропорции и особенности частей тела, а также особенности развития костной, жировой и мышечной тканей. Размеры и формы тела каждого человека генетически запрограммированы. Эта наследственная программа реализуется в… … Википедия

dic.academic.ru

Пропорция - это... Что такое Пропорция?

ПРОПОРЦИЯ — (лат., от pro для, и portio часть, порция). 1) соразмерность, согласование. 2) отношение частей между собою и к их целому. Отношение величин между собою. 3) в архитектуре: удачные размеры. Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка

ПРОПОРЦИЯ — ПРОПОРЦИЯ, пропорции, жен. (книжн.) (лат. proportio). 1. Соразмерность, определенное соотношение частей между собой. Правильные пропорции частей тела. Смешать сахар с желтком в такой пропорции: две ложки сахара на один желток. 2. Равенство двух… … Толковый словарь Ушакова

пропорция — отношение, соотношение; соразмерность. Ant. диспропорция Словарь русских синонимов. пропорция см. соотношение Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов

ПРОПОРЦИЯ — жен., франц. соразмерность; величина или количество, отвечающее чему либо; | мат. равенство содержания, одинаковые отношения двойной четы цифры; арифметическая, если второе число на столько же более или менее, первого, на сколько четвертое против … Толковый словарь Даля

ПРОПОРЦИЯ — (лат. proportio) в математике равенство между двумя отношениями четырех величин: a/b =c/d … Большой Энциклопедический словарь

ПРОПОРЦИЯ — ПРОПОРЦИЯ, в математике равенство между двумя отношениями четырех величин: a/b=с/d. Непрерывной пропорцией называют группу из трех или более величин, каждая из которых имеет одно и то же отношение к последующей величине, как, например, в… … Научно-технический энциклопедический словарь

ПРОПОРЦИЯ — ПРОПОРЦИЯ, и, жен. 1. В математике: равенство двух отношений (в 3 знач.). 2. Определённое соотношение частей между собой, соразмерность. П. в частях здания. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ПРОПОРЦИЯ — англ. proportion; нем. Proportion. 1. Соразмерность, определенное соотношение частей целого между собой. 2. Равенство двух отношений. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии

пропорция — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN ratedegreeDdegdrratio … Справочник технического переводчика

ПРОПОРЦИЯ — равенство двух (см.), т.е. а: b = с: d, где а, b, с, d члены пропорции, причём а и d крайние, b и с средине. Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних: ad = bс … Большая политехническая энциклопедия

пропорция — и; ж. [лат. proportio] 1. Соразмерное соотношение частей между собой. Соблюсти все архитектурные пропорции. Идеальная п. частей тела. 2. Определённое количественное соотношение между чем л. Нарушить пропорцию. Смешав ягоды с песком в пропорции… … Энциклопедический словарь

dal.academic.ru

составление пропорции по условию задачи

Записи с меткой "составление пропорции по условию задачи"

Задача 1. Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?

Решение. Пусть х см — толщина пачки бумаги из 500 листов. Двумя способами найдем толщину одного листа бумаги:

3,3:300 или х:500.

Так как листы бумаги одинаковые, то эти два отношения равны между собой. Получаем пропорцию (напоминание: пропорция — это равенство двух отношений):

3,3:300=х:500. Неизвестный средний член пропорции равен произведению крайних членов пропорции, деленному на известный средний член. (Подробно о пропорции и нахождению ее крайнего, среднего членов читайте в статье: «6.1.1. Пропорция. Основное свойство пропорции.»)

х=(3,3·500):300;

х=5,5. Ответ: пачка 500 листов бумаги имеет толщину 5,5 см.

Это классическое рассуждение и оформление решения задачи. Такие задачи часто включают в тестовые задания для выпускников, которые обычно записывают решение в таком виде:

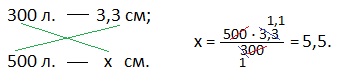
или решают устно, рассуждая так: если 300 листов имеют толщину 3,3 см, то 100 листов имеют толщину в 3 раза меньшую. Делим 3,3 на 3, получаем 1,1 см. Это толщина 100 листовой пачки бумаги. Следовательно, 500 листов будут иметь толщину в 5 раз большую, поэтому, 1,1 см умножаем на 5 и получаем ответ: 5,5 см.

Разумеется, это оправдано, так как время тестирования выпускников и абитуриентов ограничено. Однако, на этом занятии мы будем рассуждать и записывать решение так, как положено это делать в 6 классе.

Задача 2. Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?

Решение.

Вся масса арбуза (5 кг) составляет 100%. Вода составит х кг или 98%. Двумя способами можно найти, сколько кг приходится на 1% массы.

5:100 или х:98. Получаем пропорцию:

5:100 = х:98.

х=(5·98):100;

х=4,9 Ответ: в 5кг арбуза содержится 4,9 кг воды.

Задача 3. Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?

Решение.

Пусть масса 35 литров нефти составляет х кг. Тогда двумя способами можно найти массу 1 литра нефти:

16,8:21 или х:35. Получаем пропорцию:

16,8:21=х:35.

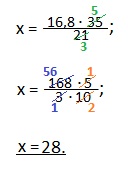Находим средний член пропорции. Для этого перемножаем крайние члены пропорции (16,8 и 35) и делим на известный средний член (21). Сократим дробь на 7.

Умножаем числитель и знаменатель дроби на 10, чтобы в числителе и знаменателе были только натуральные числа. Сокращаем дробь на 5 (5 и 10) и на 3 (168 и 3).

Ответ: 35 литров нефти имеют массу 28 кг.

Задача 4. После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?

Решение.

Пусть площадь всего поля х га, что составляет 100%. Осталось вспахать 9 га, что составляет 100% — 82% = 18% всего поля. Двумя способами выразим 1% площади поля. Это:

х:100 или 9:18. Составляем пропорцию:

х:100 = 9:18.

Находим неизвестный крайний член пропорции. Для этого перемножаем средние члены пропорции (100 и 9) и делим на известный крайний член (18). Сокращаем дробь.

Ответ: площадь всего поля 50 га.

www.mathematics-repetition.com

Пропорция - это... Что такое Пропорция?

dic.academic.ru

Пропорция (математика) | Наука | FANDOM powered by Wikia

Рис.1, Пропорция отрезков, например,AB:АС = AD:AE

‎Пропо́рция (математика) (лат. proportio — соразмерность, выровненность частей), равенство отношений числовых величин, т. е. равенство вида a : b = c : d (AB:AC=AD:AE) или, в других обозначениях, равенство $ \ \frac ab=\frac cd $ (часто читается как: «a относится к b так же, как c относится к d»). Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции. [1]

Где:

AB = a — отрезок (крайний)
AC = b — (средний)
AD = c — (средний)
AE = d — (крайний)

Пропорция (математика) в отличие от золотого сечения содержит разные значения средних членов (вместо b·b имеем b·c или b·c = a·d).

Основные свойства пропорций Править

Обращение пропорции. Если возьмём соотношения в виде: a : b = c : d, то b : a = d : c
Перемножение членов пропорции крест-накрест. Если a : b = c : d, то ad = bc.
Перестановка средних и крайних членов. Если a : b = c : d, то

Увеличение и уменьшение пропорции. Если a : b = c : d, то

Составление пропорции сложением и вычитанием. Если a : b = c : d, то

Золотое сечение Править

(Рис.2) Cхема пропорциональных отрезков золотого сечения

Отношение частей в этой пропорции выражается квадратичной иррациональностью

Т. е. (см.Рис.2) равенство вида (a + b):a = a : b, или, в других обозначениях, равенство $ \! \frac {a + b}{a}=\frac {a}{b}=\phi $ (часто читается как: «(a + b) относится к a так же, как a относится к b»). Если (a + b):a = a : b, то (a + b) и b называют крайними, а a — средними членами пропорции.[2]

Золотое сечение в отличие от пропорции содержит произведение определённых значений средних членов (вместо c·d имеем a·a или a·c = a·a). Не любое деление отрезка даёт среднее сечение. Например, деление отрезка на части, выраженных рациональными числами или на равные части, не даёт золотого сечения.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.

Золотое сечение и иррациональностьПравить

Золотое сечение в пятиконечной звезде

$ \varphi $ представляется в виде бесконечной цепочки квадратных корней:

Построение золотого сечения

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны $ \varphi $).

Геометрическое построение. Золотое сечение отрезка $ AB $ можно построить следующим образом: в точке $ B $ восстанавливают перпендикуляр к $ AB $, откладывают на нём отрезок $ BC $, равный половине $ AB $, на отрезке $ AC $ откладывают отрезок $ AD $, равный $ AC-CB $, и наконец, на отрезке $ AB $ откладывают отрезок $ AE $, равный $ AD $. Тогда

Золотое сечение — пропорция и гармония в искусстве Править

Длительное время существовало общепринятое суждение, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные Например, пропорции золотого сечения находят в пирамиде Хеопса, в соотношении размеров некоторых храмов, барельефов; предметов быта и украшений из гробницы Тутанхамона. По мнению первых исследователей, это свидетельствует, что египетские мастера пользовались соотношениями золотого сечения при их создании.

Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. Древнеегипетский зодчий Хесира, вырезанный на деревянной доске, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.

К тем же выводам пришёл Розенов в статье «Закон золотого сечения в поэзии и музыке» (1925) на примере произведений Баха, Моцарта, Бетховена.

ru.science.wikia.com