Определение прочности и модуля упругости при статическом изгибе полимерных материалов. Модуль упругости материалов таблица
Модуль Юнга (упругости) для стали и других материалов: определение, смысл
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
stankiexpert.ru
Показатель предела нагрузки на сталь — модуль упругости Юнга
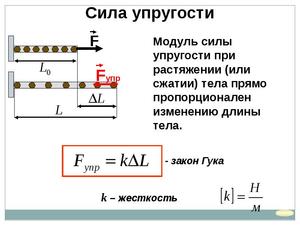До того, как взять в работу какой-то строительный материал, необходимо изучить его прочностные данные и возможное взаимодействие с другими веществами и материалами, их сочетаемость в плане адекватного поведения при одинаковых нагрузках на конструкцию. Определяющая роль для решения этой задачи отводится модулю упругости – его называют ещё модулем Юнга.
Высокая прочность стали позволяет использовать её при строительстве высотных зданий и ажурных конструкций стадионов и мостов. Добавки в сталь некоторых веществ, влияющих на её качество, называют легированием, и эти добавки могут увеличить прочность стали в два раза. Модуль упругости стали легированной гораздо выше, чем обычной. Прочность в строительстве, как правило, достигается подбором площади сечения профиля в силу экономических причин: высоколегированные стали имеют более высокую стоимость.
Далее, будет рассмотрено значение термина, изменчивость его для стали различных сортов. Для сравнения будут приведены значения модуля других материалов.
Физический смысл
Обозначение модуля упругости как физической величины – (Е), этот показатель характеризует упругую сопротивляемость материала изделия прилагаемым к нему деформирующим нагрузкам:
- продольным – растягивающим и сжимающим;
- поперечным – изгибающим или исполненным в виде сдвига;
- объёмным – скручивающим.
Чем выше значение (Е), тем выше сопротивляемость материала нагрузкам, тем прочнее будет изделие из этого материала и тем выше будет предел разрушения. Например, для алюминия эта величина составляет 70 ГПа, для чугуна – 120, железа – 190, а для стали до 220 ГПа.
Определение
Модуль упругости – сводный термин, вобравший в себя другие физические показатели свойства упругости твёрдых материалов – под воздействием силы изменяться и обретать прежнюю форму после её прекращения, то есть, упруго деформироваться. Это отношение напряжения в изделии – давление силы на единицу площади, к упругой деформации (безразмерная величина, определяемая отношением размера изделия к его изначальному размеру). Отсюда и его размерность, как и у напряжения – отношение силы к единице площади. Поскольку напряжение в метрической СИ принято измерять в Паскалях, то и показатель прочности – тоже.
Существует и другое, не очень корректное определение: модуль упругости – это давление, способное удлинить изделие вдвое. Но предел текучести большого количества материалов значительно ниже прилагаемого давления.
Модули упругости, их виды
Способов изменения условий приложения силы и вызываемых при этом деформаций много, и это предполагает и большое количество видов модулей упругости, но на практике сообразно деформирующим нагрузкам выделяют три основных:
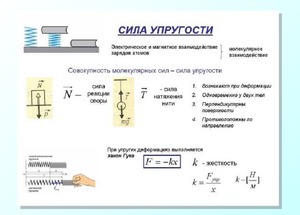Юнга (Е) представляет упругую сопротивляемость растягивающим и сжимающим нагрузкам – собственно, именно этим термином пользуются, когда говорят о модуле упругости;- модуль сдвига (G) характеризует сопротивляемость любому нарушению формы без её разрушения или изменения нормы – это отношение сдвигающей нагрузки к деформации, проявляющейся в виде изменчивости прямого угла между двумя половинами плоскости, подвергшейся нагрузке. Второе название этого термина – жёсткости, он же представляет и вязкость материала;
- модуль объёмной упругости (К) – сопротивляемость изменению объёма при разносторонних нормально приложенных напряжениях, имеющих равную величину по всем векторам. Его называют ещё модулем объёмного сжатия, выражается отношением объёмного давления к объёмной деформации сжатия.
Этими показателями характеристики упругости не исчерпываются, есть и другие, которые несут другую информацию, имеют иную размерность и смысл. Это также широко известные среди специалистов показатели упругости Ламе и коэффициент Пуассона.
Как определить модуль упругости стали
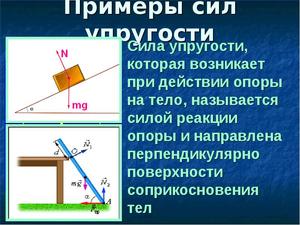Для определения параметров различных марок стали существуют специальные таблицы в составе нормативных документов в области строительства – в строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ). Так, модуль упругости (Е) или Юнга, у чугуна белого и серого от 115 до 160 ГПа, ковкого – 155. Что касается стали, то модуль упругости стали С245 – углеродистой имеет значения от 200 до 210 ГПа. Легированная сталь имеет показатели несколько выше – от 210 до 220 ГПа.
Та же самая характеристика у рядовых марок стали Ст.3 и Ст.5 имеет то же значение – 210 ГПа, а у стали Ст.45, 25Г2С и 30ХГС – 200 ГПа. Как видим, изменчивость (Е) для различных марок стали незначительна, а вот в изделиях, например, в канатах – другая картина:
- у прядей и свивок проволоки высокой прочности 200 ГПа;
- стальные тросы с металлическим стержнем 150 ГПа;
- стальные канаты с органическим сердечником 130 ГПа.
Как можно заметить, разница значительная.
Значения модуля сдвига или жёсткости (G) можно увидеть в тех же таблицах, они имеют меньшие значения, для прокатной стали – 84 ГПа, углеродистой и легированной – от 80 до 81 гпа, а для сталей Ст.3 и Ст.45–80 ГПа. Причиной различия значений параметра упругости является одновременное действие сразу трёх основных модулей, рассчитываемых по разным методикам. Однако разница между ними небольшая, что говорит о достаточной точности изучения упругости. Поэтому не стоит зацикливаться на вычислениях и формулах, а следует принять конкретную величину упругости и пользоваться ей как константой. Если не производить вычисления по отдельным модулям, а сделать расчёт комплексно, значение (Е) будет составлять 200 ГПа.
Необходимо понимать, значения эти разнятся для сталей с разными присадками и стальных изделий, включающих детали из других веществ, но разнятся эти значения незначительно. Основное влияние на показатель упругости оказывает содержание углерода, а вот способ обработки стали – горячий прокат или холодная штамповка, значительного влияния не оказывает.
При выборе стальных изделий пользуются также и ещё одним показателем, который регламентируется так же, как и модуль упругости в таблицах изданий ГОСТ и СНиП – это расчётное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Размерность у этого показателя та же, что и у модуля упругости, но значения на три порядка меньше. Этот показатель имеет два назначения: нормативное и расчётное сопротивление, названия сами говорят за себя – расчётное сопротивление применяется при выполнении расчётов прочности конструкций. Так, расчётное сопротивление стали С255 при толщине проката от 10 до 20 мм – 240 МПа, при нормативном 245 МПа. Расчётное сопротивление проката от 20 до 30 мм чуть ниже и составляет 230 МПа.
instrument.guru
| Алюминиймодуль упругости алюминия | 7.1 · 1010 (Ньютон / Метр2) |
| Вольфраммодуль упругости вольфрама | 39 · 1010 (Ньютон / Метр2) |
| Германиймодуль упругости германия | 8.1 · 1010 (Ньютон / Метр2) |
| Дюралюминиймодуль упругости дюралюминия | 7.3 · 1010 (Ньютон / Метр2) |
| Иридиймодуль упругости иридия | 52.8 · 1010 (Ньютон / Метр2) |
| Константанмодуль упругости константана | 16.3 · 1010 (Ньютон / Метр2) |
| Латуньмодуль упругости латуни | 9.8 · 1010 (Ньютон / Метр2) |
| Марганецмодуль упругости марганца | 12.4 · 1010 (Ньютон / Метр2) |
| Медьмодуль упругости меди | 12.3 · 1010 (Ньютон / Метр2) |
| Плексигласмодуль упругости плексигласа | 0.32 · 1010 (Ньютон / Метр2) |
| Полистиролмодуль упругости полистирола | 0.32 · 1010 (Ньютон / Метр2) |
| Свинецмодуль упругости свинца | 1.6 · 1010 (Ньютон / Метр2) |
| Серебромодуль упругости серебра | 7.9 · 1010 (Ньютон / Метр2) |
| Стальмодуль упругости стали | 20.6 · 1010 (Ньютон / Метр2) |
| Стекло кварцевоемодуль упругости кварцевого стекла | 7.5 · 1010 (Ньютон / Метр2) |
| Стекло оконное модуль упругости оконного стекла | 7 · 1010 (Ньютон / Метр2) |
| Фарформодуль упругости фарфора | 5.8 · 1010 (Ньютон / Метр2) |
| Чугунмодуль упругости чугуна | 10.8 · 1010 (Ньютон / Метр2) |
www.fxyz.ru
Модуль упругости некоторых материалов - стр.2
Модуль упругости некоторых материалов
| Наименование материала | Модуль Юнга | |
| Алмаз | 12 ∙10" | |
| Сталь | 2,0-2,2 ∙10" | |
| Чугун белый | 1,15-1,6 ∙10" | |
| Медь прокатная | 1,1 ∙10" | |
| Стекло | 0,56 ∙10" | |
| Алюминий катаный | 0,69 ∙10" | |
| Гранит | 0,49 ∙10" | |
| Свинец | 0,17 ∙10" | |
| Дерево | 0,1∙ 10" | |
| Каучук | 0,00008 ∙10" | |
Различие в величине модуля упругости для разных кристаллов объясняется различием в силах межатомных связей. Преобразовав выражение (6), можно получить:
(7)
или
(8)
Сравнивая полученное выражение с известной формулой закона Гука
F= kх,
мы получаем возможность выразить коэффициент жесткости k через модуль упругости Е, длину растягиваемого стержня lо и площадь его поперечного сечения S:
(9)
Выражение (6) можно рассматривать как другую формулировку закона Гука для деформации растяжения или сжатия, пользуясь которой можно рассчитать относительное изменение образца по заданному напряжению и известному модулю упругости.
Тема 3. Диаграмма растяжения. Зависимость относительного удлинения образца от величины приложенного к нему напряжения является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси ординат обычно откладывается величина механического напряжения , приложенного к образцу, а по оси абсцисс—относительное удлинение . Диаграмма растяжения показана на рисунке 4.
При небольших напряжениях (линейный участок ОА) относительное удлинение прямо пропорционально напряжению, т. е. выполняется закон Гука (6). Это обусловлено тем, что при небольших изменениях межатомных расстояний зависимость смещений атомов из равновесных положений от силы взаимодействия можно считать приблизительно линейной. При снятии напряжения атомы возвращаются в равновесные положения и форма тела практически восстанавливается. При дальнейшем увеличении напряжения деформация еще остается упругой, но ее зависимость от напряжения перестает быть линейной (участок АВ). Наибольшее напряжение Оп, до которого справедлив закон Гука, называют пределом пропорциональности. Предельное напряжение Оу (ордината точки В), при котором деформация еще остается упругой, называется пределом упругости.
Участок АВ невелик, т. е. значения предела упругости Оу и предела пропорциональности Оп настолько близки, что часто их считают совпадающими. Обычно для металлов деформация является упругой, если 0,2%.
При напряжениях, превышающих предел упругости Оу, образец после снятия нагрузки не восстанавливает свою форму (пунктирная кривая). Такие деформации называют остаточными или пластическими. Мерой остаточной деформации служит отрезок ост. Рис.4
В области пластической деформации (участок ВСD) деформация происходит почти без увеличения напряжения. На горизонтальном участке СD материал как бы течет.
Напряжение От (ордината С), при котором материал течет, называют пределом текучести.
Материалы, у которых область текучести СD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называют хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.
Из сравнения диаграмм растяжения чугуна и стали, показанных на рисунке 5, видно, что эти материалы примерно одинаково ведут себя в области упругих деформаций, т. е. они в равной мере упруги. Но в противоположность стали, имеющей значительную область пластической деформации, у чугуна эта область чрезвычайно мала. Поэтому
чугун гораздо более хрупок, чем сталь.
Как видно из диаграммы растяжения, для дальнейшего увеличения деформации необходимо снова увеличить напряжение (поднимающийся участок DЕ). В том, что материал в процессе деформации может упрочняться, можно убедиться сгибанием толстого медного прута или пластины. Для того чтобы разогнуть образец, требуются заметно большие усилия, чем для его сгибания. Объяснение этому явлению будет дано далее.
После точки Е кривая идет вниз и дальнейшая деформация вплоть до разрыва происходит при все меньшем напряжении. Наибольшее напряжение Опр, которое способен выдержать образец без разрушения, называют пределом прочности.
В таблице № 2 приведены значения прочности на разрыв для некоторых материалов.
Таблица 2 Значения прочности на разрыв для некоторых материалов
190 •107
20-30 ∙1077-15 • 107 7 107
15-60•10 12-40 •107 20-24• 107
10 - 107 0,3∙ 107
3-20 • 107 0,5 • 107 35 ∙107 70 • 107
Сталь высокопрочнаяСталь прокатная низкоуглеродистая
Чугун
Алюминий чистый
Алюминиевые сплавы
Латунь
Медь
Дерево (ель)
вдоль волокон
поперек волокон Стекло оконное Кирпич
Шелк
Льняное волокно
Твердость. Не все механические свойства материалов описываются диаграммой растяжения. Важной характеристикой материала является его твердость. Твердость характеризует способность материала оказывать сопротивление проникновению в него другого тела, т. е. способность противодействовать вдавливанию или царапанью. При измерении твердости методом вдавливания преодолеваются силы, препятствующие скольжению частиц, а в методе царапанья—силы сопротивления отрыву частиц. Поэтому результаты измерения твердости различными методами не всегда дают совпадающие результаты.
При определении твердости методом вдавливания в испытуемый образец с помощью гидравлического пресса вдавливается стальной закаленный шарик, который после снятия нагрузки оставляет на образце отпечаток в виде лунки. Чем тверже материал, тем на меньшую глубину проникает шарик и тем меньшую площадь поверхности 5 имеет лунка. Твердость при одном и том же радиусе шарика определяется отношением:
,
где F—сила, действующая на шарик. Твердость измеряется в .
В другом методе измерения твердости из двух материалов более твердым считается тот, который оставляет царапину на другом. Проведя краем стеклянного осколка по медной пластинке, мы получим царапину. В то же время с помощью медной пластины нельзя получить царапину на стекле. Значит, стекло тверже меди.
Моос предложил условную шкалу, в которой твердость оценивается царапаньем минералами, которые приняты за эталонные (табл.3).
Таблица 3
Эталонные материалы и соответствующие им значения твердости в единицах шкалы Мооса
| Минерал | Алмаз | Корунд | Топаз | Кварц | Полевой шпат | Апатит | Флюорит | Кальций | Гипс | Тальк |
| Твердость по Моосу | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Тема 4. Анизотропия механических свойств твердых тел. Рассматривая механические свойства твердых тел, мы не задумывались над тем, влияет ли направление действия силы на величину деформации. Одинаковы или различны в различных направлениях модуль упругости, предел прочности, твердость и другие характеристики?
Опыт показывает, что у многих материалов, широко применяемых в технике, механические свойства во всех направлениях одинаковы.
С другой стороны, у ряда твердых тел механические свойства и соответствующие им характеристики — модуль упругости, предел прочности и другие—зависят от направления действия силы.
Тела, физические свойства которых во всех направлениях одинаковы, называют изотропными. Тела, обладающие различными свойствами в разных направлениях, называют анизотропными
Диаграмма растяжения стали Рис.6Анизотропия характерна для монокристаллов. Все монокристаллы в той или иной мере анизотропны. В зависимости от направления, выбранного для измерений, монокристалл обладает различной упругостью, прочностью и другими физическими параметрами.
В чем же причина анизотропии монокристаллов? На рисунке 6 условно изображено расположение атомов
в одной из плоскостей монокристалла. Через узлы этой плоской решетки проведены различно ориентированные параллельные прямые. Видно, что на единицу длины прямых, принадлежащих к различным семействам, приходится неодинаковое количество атомов. Но механические свойства кристалла зависят от плотности размещения образующих его частиц. Из сказанного можно сделать вывод, что анизотропия механических свойств является следствием правильного чередования атомов в монокристаллах.
Наименее анизотропны монокристаллы с кубической, наиболее симметричной решеткой. Но анизотропия и в этом случае значительна. Так, предел прочности монокристалла меди. обладающего кубической гранецентрированной решеткой, при растяжении вдоль ребра куба равен 1,5∙108н/м2, а при растяжении вдоль диагонали куба —3,5∙108н/м2.
Физические свойства монокристаллов зависят от направления, а не от места: они одинаковы в различных местах, но различны в различных направлениях. В этом нетрудно убедиться, если, например, на поверхность пластинки слюды поставить острие иглы и нанести по ней легкий удар молотком. При рассматривании поврежденной поверхности в лупу хорошо видны так называемые фигуры удара—совокупность трещин, расположенных в направлениях минимальной прочности кристалла. Фигуры удара на слюде всегда имеют вид шестилучевых звездочек, соответствующие лучи-трещины которых параллельны. Фигуры удара на гипсе имеют вид четырехлучевых звезд. Аналогичные опыты с изотропными телами, например со стеклом, всегда дают случайные, невоспроизводимые фигуры удара. Вид фигур удара на слюде, гипсе и стекле представлен на фотографии.
Ярко выраженной анизотропией механических свойств обладают монокристаллы асбеста, графита и слюды, решетки которых имеют слоистую структуру. Слюда легко расслаивается на лепестки. Опытные экспериментаторы получают листочки слюды толщиной 10-5см. Но слюду трудно разрезать ножом в перпендикулярном слою направлении. Это обусловлено тем, что силы связи между атомами внутри слоев больше, чем силы связи между слоями. В монокристаллах асбеста имеется всего одно направление повышенной прочности. Поэтому асбест легко расчленяется на нити. Из нитей асбеста делают несгораемые веревочные пожарные лестницы, несгораемые ткани, из которых шьют спецодежду для работы в горячих цехах.
В противоположность монокристаллам поликристаллические тела изотропны, хотя и состоят из анизотропных кристаллитов. В большинстве случаев кристаллиты ориентированы хаотично, дальний порядок не распространяется на весь поликристалл и анизотропия не наблюдается. Свойства отдельных кристаллитов усредняются по всем направлениям и в среднем оказываются одинаковыми. Поэтому поликристаллические тела, к которым принадлежит большинство применяемых в технике металлов, обычно изотропны. Но при некоторых видах обработок (волочение и др.) может произойти преимущественная ориентация кристаллитов в определенном направлении. Тогда свойства отдельных кристаллитов не усредняются по всем направлениям и поликристаллическое тело оказывается анизотропным.
Тема 5. Значение законов деформаций. Знание законов деформаций имеет огромное значение для техники. В наше время учение о прочности - это большая отрасль науки, позволяющая рассчитывать конструкции зданий, мостов, корпусов кораблей, фюзеляжей самолетов и других сооружений и деталей.
Выдающимся достижением инженерной и строительной техники является Останкинская телевизионная башня в Москве - самое высокое сооружение в мире. Вершина башни отстоит от ее основания на 540 м. Более чем полукилометровое тело башни и ее фундамент должны быть устойчивыми и обладать большим запасом прочности, для того чтобы веками противостоять ураганным ветрам, изменениям температуры и другим воздействиям. Главный конструктор башни лауреат Ленинской премии Н. В. Никитин рассчитал ее на ураган со скоростью ветра 43 м/сек. Статистика показывает, что в Московской области такой ураган можно ожидать один раз в 2200 лет. Основная часть башни построена из железобетона. Точный расчет позволил поставить ее на очень маленьком по сравнению с высотой фундаменте - железобетонной шайбе диаметром 70 м, шириной 8 м и толщиной 3,5 м.
Железобетонный конус низа башни разрезан арками на десять лап. Это не архитектурные украшения. Расчеты показали, что сочленения сплошного конуса основания башни, изменяющего
свои размеры при колебаниях температуры, с фундаментом, находящимся почти при постоянной температуре, привело бы к его растрескиванию. Лапы и арки нужны для того, чтобы повысить способность основания башни к упругим деформациям.
В трубчатое бетонное тело башни заложено в натянутом состоянии 150 стальных канатов диаметром 38 мм с разрывным усилием 1120 кН каждый. Эти стальные струны сжимают бетон верхней части башни с усилием 95 000 кН, а нижней части — с усилием 38 000 кН. Такой железобетон называют предварительно напряженным.
Обычный бетон обладает значительно меньшей прочностью на растяжение, чем на сжатие, а у стальных тросов прочность на растяжение велика, зато отсутствует прочность на сжатие. Предварительно напряженный железобетон лишен обоих этих недостатков. Он обладает прочностью на сжатие обычного бетона и имеет гораздо большую по сравнению с ним прочность на растяжение.
За счет того, что обращенная к Солнцу сторона башни днем нагревается, происходит удлинение освещенной ее стороны и изгиб башни в теневую сторону. При этом отклонение вершины башни от вертикали составляет 2,5 м, а иногда при совместном действии разности температур и ветра оно достигает 5 м. Только ночью в безветренную погоду башня стоит вертикально.
Упругие свойства материалов используются не только в строительном деле, но и в машиностроении, приборостроении и других областях техники. Особенно высокие требования предъявляются к материалам, идущим на изготовление деталей, подвергающихся многократным знакопеременным нагрузкам. Ясно, что в таких деталях совершенно нельзя допускать даже малых остаточных деформаций. Это достигается не только выбором материала, но и конструкцией детали. Наглядным примером является пружина балансира в часах, совершающая 1800 изгибов в час, или рессора автомобиля, испытывающая значительные переменные деформации при движении автомобиля по неровной дороге (рис. 7).
Рессора состоит из отдельных листов специальной стали, обладающей высоким значением предела упругости. Длина листов различна. Пирамидальная и пластинчатая конструкция обеспечивает рессоре переменный коэффициент жесткости, возрастающий при увеличении нагрузки. По мере увеличения нагрузки в работу вступает все большее число листов.
Все детали машин и механизмов изготавливаются со значительным, но разумным запасом прочности, для того чтобы случайные перенапряжения, возникающие при эксплуатации, не разрушали машину или конструкцию. Без знания величин пределов упругости и прочности используемых материалов инженеры-конструкторы не могли бы рационально сочетать наименьшую массу (а значит, расход материала) с необходимой надежностью конструкций и машин.
Рис. 7. Схема устройства рессоры.
Отношение предела прочности материала Опр (или предела текучести для пластичных тел) к фактически действующему напряжению о называют коэффициентом запаса прочности: k=
Например, в строительном деле коэффициент запаса прочности стальных балок установлен не менее 2,5—2,6, а для балок из хрупких материалов (чугун, бетон) не менее 3—9. Значения коэффициента запаса прочности для некоторых материалов приведены в таблице № 4.
Таблица 4
Коэффициент запаса прочности некоторых материалов
| Характер нагрузки | Материал, подвергающийся нагрузке | Коэффициент запаса |
| прочности | ||
| Статическая длительная на | Стальные конструкции из про | |
| грузка | катного металла | 2,4-2,6 |
| Статическая длительная на | Чугун, бетон | 3,0-9,0 |
| грузка | ||
| Ударные нагрузки | Сталь | 2,8-5,0 |
| Переменные нагрузки | Сталь | 5,0-15 |
Не менее важно уметь управлять пластическими свойствами материалов. Многие методы обработки — прокатка, ковка, волочение, прессование металлов основаны на использовании их пластичности. Для изготовления методом штамповки многометровых деталей подводных лодок, таких самолетов-гигантов, как «Антей», созданы уникальные прессы, способные развивать усилия в 750000 кн. Однако и такой пресс (размером в двенадцатиэтажный дом) не удовлетворяет всех запросов современной техники. Алюминий в авиации заменяется более прочными материалами — титаном и специальными сталями, для штамповки которых требуются в 5—6 раз большие усилия. Сейчас проектируются прессы на усилие в 2∙106кн.
Контрольные вопросы
1. Что называют пределом упругости и пределом прочности материала?
2 Что такое анизотропия?
3 Приведите примеры анизотропии физических свойств кристаллов.
4. Почему монокристаллы анизотропны?
5 Почему предел прочности на растяжение у предварительно напряженного железобетона выше, чем у обычного железобетона?
Тема 6. Способы повышения прочности твердых тел
Теоретическая оценка предела прочности твердого тела. При растяжении образца его прочность определяется величиной сил межатомного притяжения, рассчитанных на 1 кв.м поверхности разрыва.
Оценим предел прочности на растяжение ионного кристалла каменной соли. Для простоты будем учитывать только взаимо¬действие между ближайшими противоположно заряженными ионами натрия Nа+ и хлора С1-, расположенными по обе стороны предполагаемой поверхности разрыва.
Согласно примерным оценкам расстояние между атомами в твердом теле составляет 3 10 м.
Считая ионы точечными зарядами, удаленными на расстояние d==3∙ 10 м друг от друга, вычислим силу притяжения между двумя разноименными нонами:
На каждый ион, расположенный на поверхности разрыва, в среднем приходится площадь поперечного сечения
refdb.ru
Модули упругости материалов - Справочник химика 21
Из уравнения (5.33) видно, что ЪТ не зависит от среднего уровня нагрузок, тем не менее, недавние исследования показали, что константа термоупругости зависит от нагрузок это объясняется зависимостью модуля упругости материалов от температуры [78]. [c.169]Данные, приведенные в упомянутых таблицах, свидетельствуют о непосредственной связи собственных частот с размерами образца, а также с характеристиками упругости и плотностью материала. Поэтому широко применяют определение модуля упругости материалов по резонансным частотам стержня, изготовленного из исследуемого Материала. Чаще всего, возбуждая продольные резонансные колебания, определяют модуль упругости Е в соответствии с формулой [c.152]
Формулы для определения усилий и напряжений приведены для стыка рассматриваемых элементов. Чтобы найти усилия и напряжения в произвольном сечении элемента, следует использовать соответствующие выражения для данного элемента, суммируя алгебраически их значения от нагружения внутренним давлением и краевыми силами и моментами Мд, полученными для данной составной конструкции, причем для сферического сегмента в качестве Яд следует принимать разность (Яд — Я), учитывающую наличие распорной силы. Формулы приведены при условии, что модули упругости материалов сопрягаемых элементов конструкции одинаковы [c.270]Е и Е1—модули упругости материалов цилиндра и поршня (А И —коэффициенты Пуассона для материалов цилиндра и поршня. [c.130]
Для ряда конструкций определяющим являются не столько абсолютные значения прочности и модуля упругости материалов, сколько их удельные значения — отношение прочности и модуля упругости к плотности материала — ар/р и /р. Удельная прочность стекловолокнитов намного превосходит удельную прочность, а удельный модуль упругости соизмерим с удельным модулем упругости металлических конструкционных материалов (табл. 1У.12). [c.151]Предел прочности и модуль упругости материалов [c.371]
Жесткость элемента выбирается такой, чтобы его деформация при ударе была пренебрежимо мала по сравнению с деформацией призмы, что достигается соблюдением соотношений при выборе его материала и толщины Н йкл, где Е и р — модули упругости материалов элемента и призмы и ккл — толщины накладки и клеевого слоя. [c.110]
Среди различных факторов, оказывающих влияние на термические напряжения в покрытиях, можно выделить первичные и вторичные. К первичным следует отнести различия в значениях к. т. р. и модулях упругости материалов покрытия и металла геометрические размеры образцов ползучесть материала покрытия и металлов предел текучести металлов , интервалы размягчения покрытия, когда теряются упругие свойства материала покрытия. Эти факторы оказывают непосредственное влияние на величину напряжений в покрытиях и могут быть учтены количественно с помощью теории. термоупругости, термопластичности и т. д. [c.24]
Зависимость величины прогиба от соотношения модулей упругости можно вычислить по формуле (I. 54) и при неизвестных абсолютных величинах модулей упругости. Для определения же напряжений необходимо знать абсолютные величины модулей упругости материалов. Однако анализ деформаций позволяет получить зависимость их от соотношения модулей упругости для прогибающейся полосы [c.30]
Здесь Еб, Е, и Е — модули упругости материалов болта и частей шатуна Рб, я — плош,ади сечений болта и соединяемых частей шатуна 6, /1 и /2 —длины болта и соединяемых деталей. [c.258]
Расчет цилиндров высокого давления и их втулок производят по формулам для толстостенных цилиндров, учитывая напряжения при посадке втулки и различие модулей упругости материалов цилиндра и втулки. Ввиду пульсирующей нагрузки, при выборе запаса прочности принимают во внимание усталостную характеристику. материала. [c.135]
На рис. 48 показана диаграмма усилий, построенная в предположении, что модуль упругости материалов деталей не изменяется. Это допущение может быть принято при условии, что температура деталей при проведении процессов не превышает 200° С. [c.83]
Давление уплотнения /о должно быть достаточным для того, чтобы материал прокладки заполнил бы неровности от обработки уплотняемых поверхностей. Величина /о или отвечающее ему е может быть найдена экспериментально. Уравнение (8.12) по заданным параметрам и модулям упругости материалов деталей конструкций и величине затяга Q позволяет найти ркр- [c.216]
Уравнение (13.15) по заданным параметрам и модулям упругости материалов деталей конструкций и величине затяга О позволяет найти Ркр. [c.396]
Епр — приведенный модуль упругости материалов шестерни и колеса в кГ/см -, [c.129]
Контактное давление зависит от величины натяга, модулей упругости материалов сопрягаемых деталей Е1 и и коэффициентов, учитывающих соотношение наружного и внутреннего диаметров подщипника. [c.58]
Ех, — модули упругости материалов при растяжении. [c.93]
Поскольку прочностные характеристики и модули упругости материалов, из которых изготовлены элементы конструкций колонных аппаратов, изменяются при повышении температуры, для каждого расчетного сечения (см. разд. 12.6.5) необходимо знать температуру (обычно в условиях эксплуатации, так как в условиях монтажа и испытаний температура равна температуре окружающей среды). Температура внутри корпуса задается условиями технологического процесса н обычно считается постоянной по времени и высоте корпуса. Однако в опорной обечайке в верхней ее части температура равна температуре корпуса, а в нижней — значительно ниже, поскольку нижняя часть охлаждается фундаментом. Для элементов нижнего опорного узла опорной обечайки, приваренной к корпусу колонны и теплоизолированной, расчетную температуру в рабочих условиях определяют по формуле [c.211]
Е и модули упругости материалов отверстия и вала. [c.19]
Жесткость проклад ки и болтов (С р и Се) определяются площадью прокладки и поперечного сечения болта (Fnp, Fe), толщиной прокладки и рабочей длиной болта (Л, Ц), а также модулями упругости материалов ( пр. Еб) [c.16]
Теория образования анизотропной фазы также распространена на случай, в котором раствор или расплав, содержащий жесткоцепные или полужесткоцепные макромолекулы, подвергается воздействию продольного гидродинамического поля (гл. IV). Особый интерес представляют растворы полужесткоцепных макромолекул. В этом случае образование межмолекулярных зацеплений в системе может наложиться на переход в анизотропную фазу под воздействием продольного гидродинамического поля. Явления такого типа могут происходить даже при воздействии сдвигового поля, что, по-видимому, может объяснять высокие значения модулей упругости материалов, сформованных из растворов полужесткоцепных макромолекул, неспособных образовывать анизотропные фазы в состоянии покоя (гл. VII). [c.11]
Выражая отношение напряжений как отношение модулей упругости материалов текстофаолита [c.187]
В рабочем диапазоне температур все исследованные материалы переходят из стеклообразного в высокоэластическое состояние. Модуль упругости материалов в стеклообразном состоянии практически не зависит от температуры. При переходе в высокоэластическое состояние вследствие нагрева до рабочей температуры он уменьша.ется на один-два порядка. [c.52]
chem21.info
Прочность и модуль упругости при статическом изгибе
Определение прочности материала при изгибе проводится в соответствии с ГОСТ 4648–71, а модуля упругости – по ГОСТ 9550-81.
Метод определения прочности при статическом изгибе заключается в кратковременном приложении нагрузки на образец пластмассы.
Образцы для испытаний изготавливают методом литья под давлением или механической вырезкой из пластин, полученных методом пластформования или прямого прессования. Образцы должны иметь вид бруска с размерами, указанными на рисунке 1 и в таблице 1.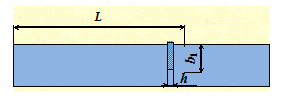 
Рисунок 1: Вид образцов для испытаний на статический изгиб
Таблица 1
| Размеры, мм | Тип образца | |
| 1 | 2 | |
| Длина L | 120±2 | Не менее 80±2 |
| Ширина b | 15±0,5 | 10±0,5 |
| Толщина h | 10±0,5 | 4±0,2 |
Для нагружения по трехточечной схеме применяют реверс (рисунок 2). Радиус наконечника 5±0,1 мм, радиус скругления опор 2±0,2 мм.
Нагружая образец до разрушения со скоростью передвижения наконечника 1–2 мм/мин (≈h/2) строят диаграмму деформирования, по максимальной нагрузке в момент разрушения определяют прочность при изгибе.
Модуль упругости при статическом изгибе определяют при нагружении образца в диапазоне до 0,2 Fp. Прогибы измеряют с погрешностью не более 0,1 мм индикатором часового типа ИЧ-10.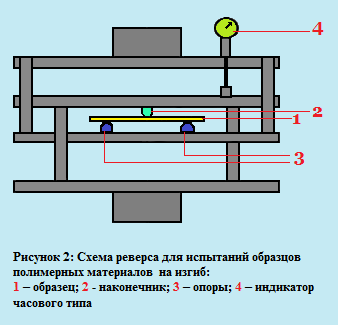
В ходе эксперимента измеряют прогибы при двух значениях нагрузки усилий F1 = (0,05–0,1)×Fр и F2 = 0,2 Fр. Отсчеты при выбранных значениях сил производят до получения стабильных показаний.
Также модуль упругости определяется по диаграмме деформирования для нагрузок и прогибов, соответствующих значениям относительной деформации 0,1% и 0,3%.
Определение модуля упругости при изгибе: экспериментальная часть
Образец устанавливают в устройство с нагружающим наконечником и опорами, которое реализует трехточечную схему нагружения (см. рисунок 2). В зависимости от толщины образца расстояние между опорами устанавливают согласно соотношению Lv=16·h±5.
Перед испытанием в средней трети образца замеряют его толщину и ширину с точностью до 0,01 мм. Образец устанавливают на опоры широкой стороной и производят нагружение наконечником по середине. Нагружение проводят плавно без толчков при постоянной скорости, равной 2 мм/мин. В процессе нагружения фиксируют нагрузку в момент разрушения. Образцы, разрушившиеся не в средней трети расстояния между опорами, в расчетах не используют.
Изгибающее напряжение σи при максимальной разрушающей нагрузке определяется так: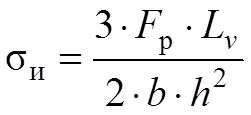
где Fp – разрушающая нагрузка, Н; Lv – расстояние между опорами, мм; b, h – ширина и толщина образца соответственно, мм.
Модуль упругости вычисляют по формуле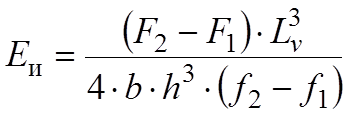 
где F1 = (0,05–0,1)×Fр и F2 = 0,2 Fр – усилия при нагружении образца, Н; f1, f2 – прогибы, соответствующие нагрузкам F1 и F2, мм; Lv – расстояние между опорами, мм; b, h — ширина и толщина образца, мм.
За результат измерения прочности и модуля упругости принимают среднее арифметическое значение для всех образцов.
Результаты испытаний заносят в протокол.
Образцы протоколов испытаний
ПРОТОКОЛ № ____ от _____________
Определения модуля упругости при изгибе по ГОСТ 9550–80
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (реверс, измеритель прогиба, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, база, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50% в течение 24 ч.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | Lv, мм | Размеры образцов, мм | Нагрузка, Н | Прогиб, мм | Еи, ГПа | |||
| h | b | F1 | F2 | f1 | f2 | |||
| 1 | ||||||||
| … | ||||||||
| Среднее арифметическое значение | ||||||||
| Среднее квадратическое отклонение | ||||||||
| Коэффициент вариации, % | ||||||||
Испытания провел:
ПРОТОКОЛ № ____ от _____________
Испытания на статический изгиб по ГОСТ 4648–71
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (реверс, измеритель прогиба, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, база, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50 % в течение 24 часов.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | Lv, мм | Размеры образцов, мм | Fp, Н | f, мм | sи, МПа | |
| h | b | |||||
| 1 | ||||||
| … | ||||||
| Среднее арифметическое значение | ||||||
| Среднее квадратическое отклонение | ||||||
| Коэффициент вариации, % | ||||||
Вид разрушения (для каждого образца) –
Испытания провел:
Список литературы: Пластмассы. Метод испытания на статический изгиб: ГОСТ 4648–71. – Взамен ГОСТ 4648–63; введ. 01.01.1973. – М.: Изд-во стандартов, 1992. – 12 с. Пластмассы. Метод определения модуля упругости при растяжении, сжатии и изгибе: ГОСТ 9550–81. – Взамен ГОСТ 9550–71; введ. 01.07.1982. – М.: ИПК Изд-во стандартов, 2004. – 8 с. Расчеты и испытания на прочность. Методы механических испытаний композиционных материалов с полимерной матрицей (композитов). Метод испытания на изгиб при нормальной, повышенной и пониженной температурах: ГОСТ 25.604–82. – Введен 01.07.84. М.: Изд-во стандартов, 1983.– 16 с.Автор: Кордикова Е.И., кандидат технических наук, доцент кафедры механики материалов и конструкций БГТУИсточник: Композиционные материалы: Лабораторный практикум, 2007 годДата в источнике: 2007 год
mplast.by
