МОДУЛЬ УПРУГОСТИ И ДЕФОРМАЦИИ БЕТОНА ПРИ. Модуль деформации бетона в30
Деформации бетона
12 мая 2016 г.
Деформативные свойства бетона определяются его начальным модулем упругости Еb. Этот модуль может быть определен в зависимости от марки или класса бетона по таблице ниже.
Начальные модули упругости тяжелого бетона
|
Класс бетона |
ВЮ |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
Модуль упругости Еb·10-3 МПа |
19 |
24 |
27,5 |
30 |
32,5 |
34,5 |
36 |
37 |
38 |
39 |
39,5 |
За начальный модуль упругости бетона при сжатии и растяжении принимается отношение нормального напряжения в бетоне к его относительной деформации при величине напряжения σb < 0,2Rb. Упругие свойства бетона следует проверить путем эксперимента, определив начальный модуль упругости вь = 0,2Rb и условный модуль деформаций при σb = 0,2Rb, подвергнув осевому сжатию призму размером 100x100x300 мм, замеряя деформацию ε = Δl/l.
При однократном непрерывном сжатии бетонного образца максимальной разрушающей нагрузкой диаграмма напряжения-деформации имеет криволинейное очертание, деформации в бетоне растут быстрее напряжений (рис. ниже). Такой характер диаграммы возникает, потому что при быстром достижении максимального усилия в бетоне под действием нагрузки одновременно с упругими деформациями развиваются также неупругие, обусловленные ползучестью бетона. Ползучесть — это способность бетона деформироваться во времени даже при неизменной нагрузке.
Диаграммы напряжения-деформации бетона при сжатии

В момент окончательного разрушения призмы получают расчетное сопротивление Rb. После этого строится график с откладыванием по оси х относительного удлинения, а по оси у — напряжения в бетоне (рис. выше).
Затем определяют:
1. начальный модуль упругости при напряжении σb = 0,2Rb (тангенс угла наклона касательной к действительной диаграмме σ-ε в начале координат)
tga0 = Eb = σb/εel
2. с увеличением напряжений угол наклона касательной к кривой σb-εb будет уменьшаться (вследствие развития во времени деформаций ползучести). Находят тангенс угла наклона к оси абсцисс касательной, проведенной к этой кривой,
tga0 = E'b = dσb/dεb
3. определяют условный модуль упругости (средний модуль упругопластичности бетона) при σb = 0,5Rb (тангенс угла наклона секущей к кривой полных деформаций)
tga1 = E'b = σb/εb
4. выражая модуль упргопластичности бетона через модуль упругости (из выражений выше), получают коэффициент упругости бетона (коэффициент Пуассона)
v = εel/εb
Коэффициент Пуассона (отношение поперечной деформации к продольной) с увеличением напряжений в бетоне возрастает: начальное его значение принимается равным 0,2.
Призменная прочность бетона может быть получена по формуле
Rb = Nmax/A
где Nmax — разрушающая нагрузка, кН; А — площадь сечения образца, см2.
ros-pipe.ru
Модуль деформации бетона
7. Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется в соответствии с законом Гука как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 1.11), т.е.
где р = 1 МПа — масштабно-размерный коэффициент.
Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал.
При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона становится величиной переменной.
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным напряжением, к оси абсцисс, т.е.
Начальный модуль упругости бетона при растяжении по абсолютной величине принимается равным , то есть , а
где vt = 0,15 — значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
Подставив в неё начальный коэффициент поперечной деформации бетона ν=0,2, получим .
ЛЕКЦИЯ 3
Арматура для железобетонных конструкций
Назначение арматуры и требования к ней
2. Виды арматуры
3. Физико-механические свойства арматурных сталей
4. Классификация арматуры по основным характеристикам. Сортамент арматуры
5. Сварные арматурные изделия
6. Соединения арматуры
1. Назначение арматуры и требования к ней
Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статической схемой работы конструкции.
Арматура в железобетонных конструкциях используется преимущественно для восприятия растягивающих усилий. Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Арматура для железобетонных конструкций должна удовлетворять следующим требованиям:
2. Виды арматуры
Многообразие видов железобетонных конструкций определяет необходимость применения широкой номенклатуры арматурных сталей.
Для изготовления арматуры используют конструкционные стали обычно с содержанием углерода не более 0,65%, так как стали с более высоким содержанием углерода плохо свариваются.
Арматура классифицируется по функциональному назначению и способу изготовления по четырём признакам.
1. По технологии изготовления арматуру делят на: стержневую горячекатаную, термомеханически упрочненную и механически упрочненную в холодном состоянии (холоднодеформированную).
2. По форме наружной поверхности арматура бывает гладкая и периодического профиля.
3. По способу применения: арматура, которую укладывают в конструкцию без предварительного напряжения, называется ненапрягаемой, арматура, которую при изготовлении конструкции предварительно натягивают — напрягаемой.
4. Арматура, устанавливаемая в железобетонных конструкциях по расчёту, называется рабочей. Площадь её поперечного сечения определяется расчётом элементов конструкций на различные нагрузки и воздействия. Её главное назначение — восприятие растягивающих усилий в сечениях. Поэтому она располагается в растянутой зоне вдоль линии действия этих усилий, т. е. перпендикулярно к возможному направлению трещин.
Арматура, устанавливаемая по конструктивным или технологическим соображениям, называется монтажной или распределительной (в плитах). Она обеспечивает проектное положение рабочей арматуры в конструкции и более равномерно распределяет усилия между отдельными стержнями рабочей арматуры. Кроме того, монтажная арматура может воспринимать обычно не учитываемые расчётом усилия от усадки бетона, изменения температуры конструкции и т. п. Она может также выполнять роль рабочей при транспортировании и монтаже конструкции.
studfiles.net
1.1.7. Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии () соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется, в соответствии с законом Гука, как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 16), т.е.:
(1.18)
где ρ = 1 МПа – масштабно-размерный коэффициет.
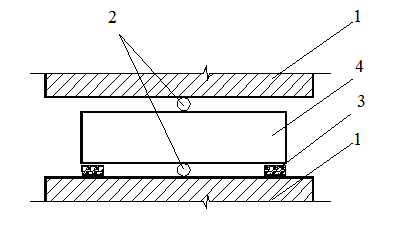
Рис. 16. Схема для определения модуля деформаций бетона:
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал, или, если известна кубиковая прочность бетона, то по различным эмпирическим формулам. Так для тяжёлого бетона естественного твердения
. (1.19)
Значение при тепловой обработке бетона снижается на 10%, при автоклавной – на 25%.
При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона становится величиной переменной.
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным напряжением, к оси абсцисс, т.е.
(1.20)
Зависимость между и можно установить, если выразить по (1.18) и (1.20) одно и то же напряжение в бетоне через упругие деформации и полные деформации
(1.21)
где v = – коэффициент упругопластичности бетона. Значение v при сжатии изменяется от 1 (при упругой работе бетона) до 0,15 (в момент, предшествующий разрушению бетона при очень длительном загружении).
Начальный модуль упругости бетона при растяжении по абсолютной величине принимается равным , т.е. , а
(1.22)
где vt = 0,15 – значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
Подставив в неё начальный коэффициент поперечной деформации бетона ν = 0,2, получим .
1.2. Арматура для железобетонных конструкций
1.2.1. Назначение арматуры и требования к ней
Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статической схемой работы конструкции.
Арматура в железобетонных конструкциях используется преимущественно для восприятия растягивающих усилий. Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Арматура для железобетонных конструкций должна удовлетворять следующим требованиям:
studfiles.net
8.5.3. Модуль упругости и деформации бетона при
КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ
Деформации бетона при приложении нагрузки зависят от его состава, свойств составляющих материалов и вида напряженного состояния. Диаграмма сжатия бетона имеет криволинейное очертание, причем кривизна увеличивается с ростом напряжений (рис. 6.4).
С увеличением прочности бетона уменьшается его деформация и кривизна диаграммы . Низкопрочные бетоны имеют даже нисходящую ветвь диаграммы сжатия. Однако на этом участке сплошность материала уже нарушена, в нем возникают микроскопические трещины, отслоение отдельных частей. В железобетонных конструкциях арматура связывает отдельные части бетона в единое целое и для частных случаев расчета конструкций необходимо учитывать нисходящую ветвь диаграммы сжатия бетона.
На характер нарастания деформаций под действием нагрузки влияют также скорость ее приложения, размеры образца, температурно-влажностное состояние бетона и окружающей среды и другие факторы. Деформация бетона включает упругую, пластическуюи псевдопластическуючасти (рис. 6.4):
Соотношение между ними зависит от состава бетона, использованных материалов и других факторов. Величина пластической и псевдопластической частей возрастает с увеличением длительности нагрузки, понижением прочности бетона, увеличением водоцементного отношения, при применении слабых заполнителей.
О деформативных свойствах бетона при приложении нагрузки судят по его модулю деформации, т. е. по отношению напряжения к относительной реформации, вызываемой его действием. Чем выше модуль деформации, тем менее деформативен материал. Поскольку диаграмма сжатия бетона криволинейна, то его модуль деформации зависит от значений относительных напряжений, постепенно понижаясь с их увеличением (рис.6.5), причем тем больше, чем ниже марка бетона. Обычно определяют либо начальный модуль деформации бетона Ео, когда преобладают упругие деформации, либо модуль деформации при определенном значении, например при= 0,5.
На практике используют эмпирические зависимости модуля деформации от различных факторов. Для расчета железобетонных конструкций важна зависимость модуля деформации при можно определить по формуле:
,
где R– прочность бетона.
В действительности модуль деформации может заметно отличаться от средних значений. В табл. 6.2 приведены значения модуля деформации при сжатии некоторых видов бетона, показывающие большое влияние на него технологических факторов.
Важное значение для расчета конструкций и оценки их поведения под нагрузкой имеют величины предельных деформаций, при которых начинается разрушение бетона, По опытным данным, предельная сжимаемость бетона изменяется в пределах 0.0015…0,003, увеличиваясь при повышении прочности бетона.
Предельную сжимаемость бетона можно также увеличивать, применяя более Деформативные компоненты и обеспечивая достаточно надежное сцепление между ними.
Предельная растяжимость бетона составляет 0,0001…0,0015, т.е. примерно в 15…20 раз меньше его предельной сжимаемости.
Предельная растяжимость повышается при введении в бетон пластифицирующих добавок, использовании белитовых цементов, уменьшении крупности заполнителей или при применении заполнителей с высокими деформативными свойствами и сцеплением с цементным камнем.
studfiles.net
6. Модуль деформации бетона и мера ползучести.
Начальный модуль упругости ЕВ бетона при сжатии – это величина, соответствующая мгновенному загружению.Геометрически – это тангенс угла наклона прямой упругих деформаций.
Модуль полных деформацийбетона при сжатиисоответствует полным деформациям, включая ползучесть. Это переменная величина. Геометрически – это тангенс угла наклона касательной к кривой в точке с заданным напряжением.
Для расчёта железобетонных конструкций используют модуль упругопластичности (секущий модуль).Это тангенс угла наклона секущей, проходящей через начало координат и любой точки, заданной на диаграмме.
Если мы выразим одно и то же напряжение через упругие деформациии полные деформации, то получим,
- коэффициент пластичности
–коэффициент упругопластичной деформации бетона
следовательно .
.
Для идеально упругого материала , для идеально пластического материала.
Зависимость между напряжениями и деформациями ползучести выражаются мерой ползучести .
где .
Мера ползучести зависит от класса бетона и его модуля упругости.
7. Реологические свойства бетона.
Усадка - уменьшение бетона в объеме при твердении в обычной среде.
Набухание - увеличение бетона в объеме при твердении вводе.
Ползучесть - свойство бетона, характеризующее нарастание неупругих деформаций с течением времени при постоянных напряжениях.
Релаксация - уменьшение с течением времени напряжений при постоянной начальной деформации.
Если испытываемый образец загрузить по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через некоторое время), то получим ступенчатую линию. Деформации, измеренные сразу, являются упругими. При достаточно большом числе ступеней загружения зависимость σb – εbстановится плавной кривой.
Опыты с бетонными призмами показывают, что независимо с какой скоростью Vбыло получено напряжениеσb1, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковые.
С ростом напряжений ползучесть увеличивается.
Многократное повторение циклов загрузки - разгрузки приводит к постепенному накапливанию εpl. После достаточно большого числа циклов неупругие деформации, соответствующие данному уровню напряжений, выбираются, ползучесть достигает своего предельного значения, бетон начинает упруго работать ().
При больших напряжениях неупругие деформации неограниченно растут, и бетон разрушается.
8. Предельные деформации бетона.
Предельная сжимаемость
растяжимость
Cувеличением класса бетона предельные деформации падают, с увеличением длительности приложения нагрузки – возрастают.
studfiles.net
vest-beton.ru
7. Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется в соответствии с законом Гука как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 1.11), т.е.
где р = 1 МПа — масштабно-размерный коэффициент.
Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал.
При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона становится величиной переменной.
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным напряжением, к оси абсцисс, т.е.
Начальный модуль упругости бетона при растяжении по абсолютной величине принимается равным , то есть , а
где vt = 0,15 — значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
Подставив в неё начальный коэффициент поперечной деформации бетона ν=0,2, получим .
ЛЕКЦИЯ 3
Арматура для железобетонных конструкций
Назначение арматуры и требования к ней
2. Виды арматуры
3. Физико-механические свойства арматурных сталей
4. Классификация арматуры по основным характеристикам. Сортамент арматуры
5. Сварные арматурные изделия
6. Соединения арматуры
1. Назначение арматуры и требования к ней
Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статической схемой работы конструкции.
Арматура в железобетонных конструкциях используется преимущественно для восприятия растягивающих усилий. Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Арматура для железобетонных конструкций должна удовлетворять следующим требованиям:
2. Виды арматуры
Многообразие видов железобетонных конструкций определяет необходимость применения широкой номенклатуры арматурных сталей.
Для изготовления арматуры используют конструкционные стали обычно с содержанием углерода не более 0,65%, так как стали с более высоким содержанием углерода плохо свариваются.
Арматура классифицируется по функциональному назначению и способу изготовления по четырём признакам.
1. По технологии изготовления арматуру делят на: стержневую горячекатаную, термомеханически упрочненную и механически упрочненную в холодном состоянии (холоднодеформированную).
2. По форме наружной поверхности арматура бывает гладкая и периодического профиля.
3. По способу применения: арматура, которую укладывают в конструкцию без предварительного напряжения, называется ненапрягаемой, арматура, которую при изготовлении конструкции предварительно натягивают — напрягаемой.
4. Арматура, устанавливаемая в железобетонных конструкциях по расчёту, называется рабочей. Площадь её поперечного сечения определяется расчётом элементов конструкций на различные нагрузки и воздействия. Её главное назначение — восприятие растягивающих усилий в сечениях. Поэтому она располагается в растянутой зоне вдоль линии действия этих усилий, т. е. перпендикулярно к возможному направлению трещин.
Арматура, устанавливаемая по конструктивным или технологическим соображениям, называется монтажной или распределительной (в плитах). Она обеспечивает проектное положение рабочей арматуры в конструкции и более равномерно распределяет усилия между отдельными стержнями рабочей арматуры. Кроме того, монтажная арматура может воспринимать обычно не учитываемые расчётом усилия от усадки бетона, изменения температуры конструкции и т. п. Она может также выполнять роль рабочей при транспортировании и монтаже конструкции.
studfiles.net
6. Модуль деформации бетона и мера ползучести.
Начальный модуль упругости ЕВ бетона при сжатии – это величина, соответствующая мгновенному загружению.Геометрически – это тангенс угла наклона прямой упругих деформаций.
Модуль полных деформацийбетона при сжатиисоответствует полным деформациям, включая ползучесть. Это переменная величина. Геометрически – это тангенс угла наклона касательной к кривой в точке с заданным напряжением.
Для расчёта железобетонных конструкций используют модуль упругопластичности (секущий модуль).Это тангенс угла наклона секущей, проходящей через начало координат и любой точки, заданной на диаграмме.
Если мы выразим одно и то же напряжение через упругие деформациии полные деформации, то получим,
- коэффициент пластичности
–коэффициент упругопластичной деформации бетона
следовательно .
.
Для идеально упругого материала , для идеально пластического материала.
Зависимость между напряжениями и деформациями ползучести выражаются мерой ползучести .
где .
Мера ползучести зависит от класса бетона и его модуля упругости.
7. Реологические свойства бетона.
Усадка - уменьшение бетона в объеме при твердении в обычной среде.
Набухание - увеличение бетона в объеме при твердении вводе.
Ползучесть - свойство бетона, характеризующее нарастание неупругих деформаций с течением времени при постоянных напряжениях.
Релаксация - уменьшение с течением времени напряжений при постоянной начальной деформации.
Если испытываемый образец загрузить по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через некоторое время), то получим ступенчатую линию. Деформации, измеренные сразу, являются упругими. При достаточно большом числе ступеней загружения зависимость σb– εbстановится плавной кривой.
Опыты с бетонными призмами показывают, что независимо с какой скоростью Vбыло получено напряжениеσb1, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковые.
С ростом напряжений ползучесть увеличивается.
Многократное повторение циклов загрузки - разгрузки приводит к постепенному накапливанию εpl. После достаточно большого числа циклов неупругие деформации, соответствующие данному уровню напряжений, выбираются, ползучесть достигает своего предельного значения, бетон начинает упруго работать ().
При больших напряжениях неупругие деформации неограниченно растут, и бетон разрушается.
8. Предельные деформации бетона.
Предельная сжимаемость
растяжимость
Cувеличением класса бетона предельные деформации падают, с увеличением длительности приложения нагрузки – возрастают.
14
studfiles.net
МОДУЛЬ УПРУГОСТИ И ДЕФОРМАЦИИ БЕТОНА ПРИ — КиберПедия
КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ
Деформации бетона при приложении нагрузки зависят от его состава, свойств составляющих материалов и вида напряженного состояния. Диаграмма сжатия бетона имеет криволинейное очертание, причем кривизна увеличивается с ростом напряжений (рис. 6.4).
С увеличением прочности бетона уменьшается его деформация и кривизна диаграммы . Низкопрочные бетоны имеют даже нисходящую ветвь диаграммы сжатия. Однако на этом участке сплошность материала уже нарушена, в нем возникают микроскопические трещины, отслоение отдельных частей. В железобетонных конструкциях арматура связывает отдельные части бетона в единое целое и для частных случаев расчета конструкций необходимо учитывать нисходящую ветвь диаграммы сжатия бетона.
На характер нарастания деформаций под действием нагрузки влияют также скорость ее приложения, размеры образца, температурно-влажностное состояние бетона и окружающей среды и другие факторы. Деформация бетона включает упругую , пластическую и псевдопластическую части (рис. 6.4):
Соотношение между ними зависит от состава бетона, использованных материалов и других факторов. Величина пластической и псевдопластической частей возрастает с увеличением длительности нагрузки, понижением прочности бетона, увеличением водоцементного отношения, при применении слабых заполнителей.
О деформативных свойствах бетона при приложении нагрузки судят по его модулю деформации, т. е. по отношению напряжения к относительной реформации, вызываемой его действием. Чем выше модуль деформации, тем менее деформативен материал. Поскольку диаграмма сжатия бетона криволинейна, то его модуль деформации зависит от значений относительных напряжений , постепенно понижаясь с их увеличением (рис.6.5), причем тем больше, чем ниже марка бетона. Обычно определяют либо начальный модуль деформации бетона Ео, когда преобладают упругие деформации, либо модуль деформации при определенном значении , например при = 0,5.
На практике используют эмпирические зависимости модуля деформации от различных факторов. Для расчета железобетонных конструкций важна зависимость модуля деформации при можно определить по формуле:
,
где R – прочность бетона.
В действительности модуль деформации может заметно отличаться от средних значений. В табл. 6.2 приведены значения модуля деформации при сжатии некоторых видов бетона, показывающие большое влияние на него технологических факторов.
Важное значение для расчета конструкций и оценки их поведения под нагрузкой имеют величины предельных деформаций, при которых начинается разрушение бетона, По опытным данным, предельная сжимаемость бетона изменяется в пределах 0.0015…0,003, увеличиваясь при повышении прочности бетона.
Предельную сжимаемость бетона можно также увеличивать, применяя более Деформативные компоненты и обеспечивая достаточно надежное сцепление между ними.
Предельная растяжимость бетона составляет 0,0001…0,0015, т.е. примерно в 15…20 раз меньше его предельной сжимаемости.
Предельная растяжимость повышается при введении в бетон пластифицирующих добавок, использовании белитовых цементов, уменьшении крупности заполнителей или при применении заполнителей с высокими деформативными свойствами и сцеплением с цементным камнем.
ДЕФОРМАЦИИ ПОЛЗУЧЕСТИ.
Под ползучестью бетона понимают его способность деформироваться во времени при длительном действии постоянной нагрузки. Физическая природа ползучести еще недостаточно выяснена, но большинство исследователей считают, что пластические деформации ползучести обусловливаются пластическими свойствами цементного камня и изменением состояния основной составляющей бетона. Деформации ползучести наиболее заметно развиваются в первые сроки после приложения нагрузки и постепенно затухают, но они наблюдаются иногда у бетона в возрасте одного года и больше. Полная деформация ползучести может значительно превосходить деформации, получаемые бетоном в момент загружения.
Ползучесть бетона зависит от еще большего числа факторов, чем его усадка, причем большинство факторов действует на деформации ползучести подобно их влиянию на деформации усадки. На ползучесть бетона влияют расход и вид цемента, водоцементное отношение , вид и крупность заполнителя, степень уплотнения бетона, степень гидратации цемента к моменту приложения нагрузки, температура и влажность окружающей среды и самого бетона, размеры образца и относительное значение напряжений в бетоне, Ползучесть бетона увеличивается при повышении содержания цемента, увеличении водоцементного отношения, уменьшении крупности заполнителей и повышении их деформативности, например, при применении пористых заполнителей.
Для оценки ползучести бетона удобно пользоваться мерой ползучести С, под которой понимается ползучесть бетона при единичной нагрузке:
,
где -полная деформация ползучести.
Ориентировочно мера ползучести
,
где - исходная мера ползучести, принимаемая равной для бетона на обычном портландцементе без ускорителей твердения и для бетона на высокопрочном цементе ; - поправочные коэффициенты, учитывающие соответственно влияние времени приложения нагрузки, В/Ц, расхода цемента, размеров сечения образца, фактической влажности воздуха.
Приведенные на рис. 6.6 графики изменения поправочных коэффициентов наглядно показывают влияние различных факторов на деформации ползучести обычного тяжелого бетона.
ТЕМПЕРАТУРНЫЕ ДЕФОРМАЦИИ
Бетон, как и другие материалы, расширяется при нагревании и сжимается при охлаждении. В среднем коэффициент линейного расширения бетона составляет . Однако в действительности он колеблется в зависимости от состава бетона и свойств заполнителей и вяжущего. С увеличением содержания цементного камня коэффициент линейного расширения увеличивается. Например, в одном из опытов раствор состава 1:3 имел , а цементный камень - . Определенное влияние на коэффициент линейного расширения оказывает вид заполнителя. Например, бетон на граните в опытах показал , бетон на керамзите - , бетон на известняке - . Зависимость коэффициента линейного расширения бетона от коэффициента линейного расширения заполнителя, приведена на рис. 6.7.
Изменение температуры в пределах 0 ... 50 °С мало влияет на коэффициент температурного расширения сухого бетона, если при этом в бетоне отсутствуют физико-химические превращения. При изменении температуры влажного бетона температурные деформации складываются с влажностной усадкой или расширением. При замерзании влажного бетона существенное влияние на его деформации оказывает образование льда в порах и капиллярах материала. В ряде случаев вместо деформации сжатия при остывании бетона ниже 0°С могут наблюдаться деформации расширения, вызываемые давлением образующегося льда.
Температурные деформации бетона близки к температурным деформациям стали, что обеспечивает их надежную совместную работу в железобетоне при различных температурах окружающей среды.
Для большей наглядности па рис.33 приведены деформации цементного камня относительно стали (линейная деформация стали принята за нуль). Из рисунка видно, что при понижении температуры деформации цементного камня относительно стали увеличиваются и достигают первого максимума ( ) при -5°С, затем они уменьшаются и переходят в отрицательные. Максимум отрицательных деформаций (до ) находится в температурном интервале от -20 до -35° С.
Такие деформации можно условно разделить на три вида в соответствии с температурными интервалами.
Деформации первого вида в зависимости от В/Ц цементного камня укладываются, как это видно на pис. 33, в температурный интервал от +20 до -15° С; деформации второго вида - от -10 до -40° С; деформации третьего вида - от -35 до -65° С.
cyberpedia.su
13. Модули деформации бетона
Начальный модуль упругости бетона при сжатии соответствует лишь упругим деформациям, возникающим при мгновенном загружении. Геометрически он определяется как тангенс угла наклона прямой упругих деформаций:, где– масштабно размерный коэффициент, МПа. Модуль полных деформаций соответствует полным деформациям (включая ползучесть) и является величиной переменной; геометрически он определяется как тангенс угла наклона касательной к кривойв точке с заданным напряжением:. Для расчета ж/б конструкций пользуются средним модулем или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей в точке на кривойс заданным напряжением:. Поскольку уголменяется в зависимости от напряжений и времени, модуль упругопластисности является также переменной величиной, меньшей, чем начальный модуль упругости. Зависимость между начальным модулем упругости бетона и модулем упругопластичности можно установить, если выразить одно и то же напряжение в бетонечерез упругие деформациии полные деформации:. Отсюда, где– коэффициент упругопластических деформаций бетона. Коэффициентизменяется от 1 (при упругой работе) до 0,15. При изгибе ж/б элементов для бетона сжатой зоныможет быть на 15…20% больше, чем при осевом сжатии. При растяжении элементов модуль упруго-пластичности бетона:, где– коэффициент упругопластических деформаций бетона при растяжении. Предельная растяжимость бетона в зависимости от временного сопротивления растяжению:. Существуют различные эмпирические формулы, в которых устанавливается зависимость между начальным модулем упругости и классом бетона. Модуль сдвига бетона:.
15.Сцепление арматуры с бетоном. Защитный слой бетона.
В ж/б конструкциях скольжение арматуры в бетоне под нагрузкой не происходит благодаря сцеплению материалов. Прочность сцепления арматуры с бетоном оценивают сопротивлением выдергиванию или выдавливанию арматурных стержней, заанкерованных в бетоне. Прочность сцепления зависит от следующих факторов: зацепления в бетоне выступов на поверхности арматуры периодического профиля, сил трения, развивающихся при контакте арматуры с бетоном под влиянием его усадки; склеивания арматуры с бетоном, возникающего благодаря клеящей способности цементного геля. Прочность сцепления возрастает при повышении класса бетона, уменьшением водоцементного отношения, а также с увеличением возраста бетона. Для лучшего сцепления арматуры с бетоном при конструировании ж/б элементов диаметр растянутых стержней следует ограничить. Среднее напряжение сцепления определяют по формуле: τс=N/(lan*u),где N-усилие в стержне, (lan*u)-площадь заделки, lan -длина анкеровки стержня, u -периметр сечения стержня.
Защитный слой бетона. Под защитным слоем бетона понимают слой бетона между наружной поверхностью конструкции и наружной поверхностью арматуры.
Защитный слой бетона для рабочей арматуры должен обеспечивать совместную работу арматуры с бетоном на всех стадиях работы конструкции, а также защиту арматуры от внешних атмосферных, температурных и подобных воздействий.
Защитный слой нормируется СНиПом “Б и ЖБК”. Он устанавливается в зависимости от видов и размеров конструкции ,в зависимости от условий эксплуатации, в зависимости от диаметра и назначения арматуры.
Толщина защитного слоя должна составлять, как правило, не менее диаметра стержня и не менее значений, указанных в табл. СНиПа “Б и ЖБК”.
studfiles.net
Модуль упругости бетона
⇐ ПредыдущаяСтр 10 из 14Следующая ⇒
| Класс бетона | В15 | В20 | В25 | В30 | В35 |
| Еb ,кПа | 20,5·106 | 24,0·106 | 27·106 | 29,0·106 | 31·106 |
Приведенное значение K получают из предположения, что влияние различных значений Kiна работу сваи уменьшается до нуля в пределах hm–мощности слоев грунта (рис. 16), определяющих в основном работу свай на горизонтальные нагрузки
hm=3,5dc+1,5. (48)
Расчетный размер сваи вычисляется по формуле
dp=Kэ(1,5dc+0,5), (49)
где Kэ=1 – для прямоугольного сечения сваи; Еb – начальный модуль упругости бетона; I – момент инерции поперечного сечения сваи; dс –размер поперечного сечения сваи, м.
Момент в голове сваи
Мв=0.
Поперечная сила в голове сваи
Qв=Qx /n, (50)
где п – количество свай; l0 – свободная длина сваи, l0=0.
Расчет изгибающего момента Мz осуществляется с помощью ЭВМ по программе КОСТ – 2. Данные для расчета сводятся в табл. 6.
Таблица 6
Исходные данные к расчету Mz, Qz, Pzь
При свободном опирании ростверка на сваи принимается MB=0. N – количество сечений свай, в которых вычисляем вышесказанные величины при ,принимаем N=18; при N=17;при ≤3,0; .
Наибольший момент по длине элемента устанавливается по эпюре Mz.
Марку сваи определяют по типовому проекту 1.001-10.1[8].
mykonspekts.ru