Упругие свойства материала. Обобщенный закон Гука. Методы определения модуля упругости. Ферромагнитная аномалия упругости. Методика оценки модуля упругости материалов
Испытания на растяжение полимерных материалов
Определение прочности материала при растяжении проводится по ГОСТ 11262, а определение модуля упругости – по ГОСТ 9550-81.
Образцы для испытаний термопластов и армированных пластиков должны соответствовать типу и размерам, указанным на рисунке и в таблице.
Рисунок 1: Образцы для испытаний материалов на растяжение (Числовые значения параметров приведены в таблице 1)
Образец типа 1 применяют для испытаний пластмасс с высоким относительным удлинением при разрыве (полиэтилен, пластифицированный поливинилхлорид), образец типа 2 – для испытаний большинства материалов (термореактивные, термопластичные и слоистые пластики), образец типа 3 в форме полоски – для испытаний стеклопластиков.
Таблица 1
| Размеры образцов, мм | Образец типа | ||
| 1 | 2 | 3 | |
| Общая длина l1, не менее | 115 | 150 | 250 |
| Расстояние между метками, определяющими положение кромок зажимов на образце, l2 | 80±5 | 115±5 | 170±5 |
| Длина рабочей части l3 | 33±1 | 60±1 | – |
| Расчетная длина l0 | 25±1 | 50±1 | 50±1 |
| Ширина головки b1 | 25±0,5 | 20±0,5 | 25±0,5 |
| Ширина рабочей части b2 | 6±0,4 | 10±0,5 | – |
| Толщина h | 2±0,2(от 1 до 3) | 4±0,4(от 1 до 10) | 2±0,2(от 1 до 6) |
Диаграмму растяжения строят при нагружении образца до разрушения. Скорость нагружения – 2,0±0,4 мм/мин. По удлинению в момент разрушения Dl определяют относительно удлинение при разрыве e.
По максимальному значению нагрузки Fpвычисляют предел прочности при растяжении.
Удлинение измеряют прибором с погрешностью не более 2% в диапазоне 0,1–0,5 мм. База преобразователя перемещения L0, устанавливаемого на образец, не менее 20 мм.
По диаграмме деформирования определяют значения нагрузок F1 и F2 и удлинение Dl1 и Dl2, соответствующих относительному удлинению 0,1% и 0,3% и рассчитывают модуль упругости при растяжении.
При невозможности записи диаграммы деформирования модуль упругости определяют при циклическом нагружении образца (до получения стабильных приращений) в диапазоне усилий F1 = (0,05–0,1)×Fр до F2 = 0,2×Fр. При значениях нагрузки F1 и F2 определяют приращение Dl на базе L0.
Испытания полимерных материалов на растяжение: экспериментальная часть
Испытания на растяжение полимерных материалов проводят при температуре 23±2°С в соответствии с ГОСТ 11262–80 и ГОСТ 9550–81.
Перед испытанием замеряют ширину и толщину образцов в рабочей части с точностью до 0,01 мм не менее чем в трех местах и вычисляют площадь поперечного сечения. В расчет принимают наименьшую площадь поперечного сечения.
Перед испытанием на образец наносят необходимые метки (без повреждения образцов), ограничивающие его базу и положение кромок захватов (таблица).
Образцы закрепляют в зажимы испытательной машины по меткам, определяющим положение кромок зажимов, таким образом, чтобы продольные оси зажимов и ось образца совпадали между собой и с направлением движения подвижного зажима. Зажимы затягивают равномерно, чтобы не было проскальзывания образца в процессе испытания, но при этом не происходило его разрушение в месте закрепления. Далее настраивают прибор для замера деформаций.
Затем образец нагружают возрастающей нагрузкой, величину которой фиксируют по шкале динамометра. Скорость нагружения составляет 25 мм/мин при определении прочности и относительного остаточного удлинения. В момент разрушения фиксируют наибольшее усилие и определяют прочность при растяжении по формуле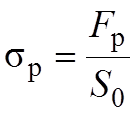
где Fp – нагрузка, при которой образец разрушился, Н; S0 = b×h – начальное поперечное сечение образца, мм2; b, h – ширина и толщина образца соответственно, мм.
Образцы, разрушившиеся за пределами рабочей части, за результат не принимают.
По удлинению в момент разрушения Dl определяют относительное удлинение при разрыве e:
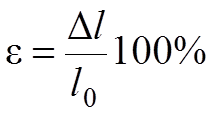 где Dl – изменение расчетной длины образца в момент разрыва, мм; l0 – расчетная длина, мм.
где Dl – изменение расчетной длины образца в момент разрыва, мм; l0 – расчетная длина, мм.
Модуль упругости определяют по формуле
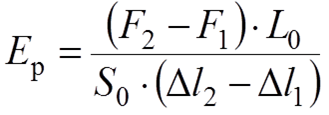 где F1, F2 – значения нагрузок, соответствующих относительному удлинению 0,1% и 0,3%, Н; Dl1, Dl2 – удлинение при нагрузках F1, F2 соответственно, мм.
где F1, F2 – значения нагрузок, соответствующих относительному удлинению 0,1% и 0,3%, Н; Dl1, Dl2 – удлинение при нагрузках F1, F2 соответственно, мм.
За результат измерения прочности, относительного удлинения и модуля упругости принимают среднее арифметическое значение для всех образцов.
Результаты испытаний заносят в протокол.
Образцы протоколов испытаний на растяжение
ПРОТОКОЛ № ____ от _____________
Испытания на растяжение по ГОСТ 11262–80
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (измеритель удлинения, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50% в течение 24 ч.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | l0, мм | Размеры образцов, мм | S0, мм2 | F, Н | sр, МПа | |
| h | b | |||||
| 1 | ||||||
| … | ||||||
| Среднее арифметическое значение, МПа | ||||||
| Среднее квадратическое отклонение | ||||||
| Коэффициент вариации, % | ||||||
Испытания провел:
ПРОТОКОЛ № ____ от _____________
Определения модуля упругости при растяжении по ГОСТ 9550–81
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (измеритель удлинения, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, база, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50 % в течение 24 часов.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | l0, мм | Размеры образцов, мм | S0, мм2 | Нагрузка, Н | Удлинение, мм | Ер, ГПа | |||
| h | b | F1 | F2 | l1 | l2 | ||||
| 1 | |||||||||
| … | |||||||||
| Среднее арифметическое значение | |||||||||
| Среднее квадратическое отклонение | |||||||||
| Коэффициент вариации, % | |||||||||
Испытания провел:
Читайте также: Механические свойства полимеров
Список литературы: Пластмассы. Метод определения модуля упругости при растяжении, сжатии и изгибе: ГОСТ 9550–81. – Взамен ГОСТ 9550–71; введ. 01.07.1982. – М.: ИПК Изд-во стандартов, 2004. – 8 с. Пластмассы. Метод испытания на растяжение: ГОСТ 11262–80. – Взамен ГОСТ 11262–76; введ. 01.12.1980. – М.: Изд-во стандартов, 1986.– 16 с. Пластмассы. Методы механических испытаний. Общие требования: ГОСТ 14359–69. – Введен 01.01.1970. – М.: Изд-во стандартов, 1979.– 21 с. Расчеты и испытания на прочность. Методы механических испытаний композиционных материалов с полимерной матрицей (композитов). Метод испытания плоских образцов на растяжение при нормальной, повышенной и пониженной температурах: ГОСТ 25.601–80. – Введен 01.07.81. – М.: Изд-во стандартов, 1980.– 16 с.Автор: Кордикова Е.И., кандидат технических наук, доцент кафедры механики материалов и конструкций БГТУИсточник: Композиционные материалы: Лабораторный практикум, 2007 годДата в источнике: 2007 год
mplast.by
Упругие свойства материала. Обобщенный закон Гука. Методы определения модуля упругости. Ферромагнитная аномалия упругости
9. УПРУГИЕ СВОЙСТВА МАТЕРИАЛА
9.1. Основные понятии
Под упругостью понимают способность материала восстанавливать первоначальную форму и размеры после снятия внешних механических нагрузок. Упругость, также как и другие физические свойства, может быть использована для исследования металлов и сплавов при решении задач материаловедения.
Основными количественными характеристиками упругости являются модуль нормальной упругости (Е), модуль сдвига (G) и модуль объемной упругости или модуль всестороннего сжатия (D), вычисляемые как первая производная изменения степени линейной, угловой и объемной деформации от приложенной внешней нагрузки в области проявления закона Гука. Все три модуля упругости связаны между собой соотношениями
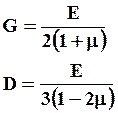 (9.1)
(9.1)
где μ – коэффициент Пуассона.
Коэффициент Пуассона характеризует изменение объема тела при упругой деформации. При одноосном растяжении образца квадратного сечения увеличение объема вследствие его удлинения частично компенсируется поперечным сужением. Аналогичные процессы, но с противоположным знаком происходят при одноосном сжатии. Коэффициент Пуассона в этом случае определяется
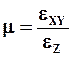 (9.2)
(9.2)
где εZ, εXY – относительное изменение продольных и поперечных размеров образца
Для большинства металлов и сплавов коэффициент Пуассона находится в пределах 0,25…0,35; наименьшее значение найдено для Be (μ = 0.039), а наибольшее у Pb (μ = 0,44), Tl и In (μ = 0,46).
Для большинства металлов и сплавов выполняется соотношение
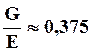 …0,382 (9.3)
…0,382 (9.3)
Упругие свойства определяются силами связей между соседними элементарными частицами в материале (атомами или ионами). Рассмотрим, как изменяется потенциальная энергия пары соседних частиц U в зависимости от разделяющего их расстояния r (рис.9.1). Равновесное расстояние между частицами r0 соответствует минимуму потенциальной энергии. Этот минимум образуется в результате уравновешивания энергий отталкивания и притяжения между двумя соседними атомами или ионами.

Рис. 9.1. Изменение потенциальной энергии (а) и силы (б) взаимодействия от расстояния между атомами (или ионами) материала
Уравнение потенциальной энергии задается выражением
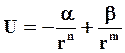 (9.4)
(9.4)
где первое слагаемое описывает энергию притяжения, а второе – энергию отталкивания. В точке r0 расстояние между частицами соответствует равновесному состоянию, при котором потенциальная энергия достигает минимума. Сила взаимодействия между частицами определяется
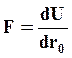 (9.5)
(9.5)
В точке r0 сила, действующая на частицы равна нулю.
Первая производная от силы по расстоянию, разделяющему частицы, описывает жесткость или обоюдное сопротивление частиц разделению друг от друга
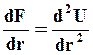 (9.6)
(9.6)
Выражение (9.6) представляет аналог модуля Юнга, который в упругой области пропорционален второму слагаемому, т.е.
 (9.7)
(9.7)
Следовательно, модуль упругости определяется равновесным расстоянием между частицами. С повышением температуры значение r0 возрастает, приводя к уменьшению модуля упругости.
Поскольку модуль упругости Е зависит от прочности сил межатомной связи, которые изменяются только сообразно типу взаимодействия частиц в том или ином конкретном материале, этот параметр практически не чувствителен к изменениям микроструктуры. Этот факт находит экспериментальное подтверждение. Так, если термообработкой и легированием можно сильно изменить структуру и повысить прочность стали на один порядок и более, то модуль упругости при этом возрастает всего на 5…10%.
9.2. Обобщенный закон Гука
Закон Гука можно обобщить для случая многоосного нагружения, как изотропного, так и анизотропного материала. Напряжение, действующее в одном направлении (допустим вдоль оси Y) вызовет
vunivere.ru
способ определения модуля упругости материала - патент РФ 2272274
Изобретение относится к способам определения модуля упругости материала. Способ заключается в том, что на образец исследуемого материала воздействуют свободно падающим индентором шарообразной формы с известными свойствами и измеряют время между первым и вторым соударениями индентора с образцом, при этом дополнительно измеряют время удара индентора с образцом. Выполняют расчет модуля упругости с помощью расчетной упруговязкой модели с использованием экспериментально найденных значений, для чего заменяют систему образец исследуемого материала - индентор на этапе их контакта расчетной упруговязкой моделью. Задают предварительное значение коэффициента жесткости упругого элемента данной модели и рассчитывают время между первым и вторым соударениями модели с образцом, подбирая при этом численное значение коэффициента вязкости вязкого элемента расчетной упруговязкой модели, при котором значение времени между первым и вторым соударениями модели совпадает с измеренным значением времени между первым и вторым соударениями индентора с образцом. При выбранном численном значении коэффициента вязкости вязкого элемента модели рассчитывают время удара модели с образцом, подбирая при этом численное значение коэффициента жесткости упругого элемента модели. О модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента расчетной упруговязкой модели, при котором время удара расчетной упруговязкой модели совпадает с измеренным временем удара индентора. Технический результат - повышение достоверности, расширение области применения, упрощение способа. 2 ил., 1 табл. 
Рисунки к патенту РФ 2272274
Изобретение относится к способам определения физико-механических свойств материалов путем приложения одиночного ударного усилия, а именно к способам определения модуля упругости материала, и может быть использовано при решении целого ряда практических и теоретических задач, для выполнения которых необходима информация об упругих свойствах материалов и сред, а также об изменении данных свойств вследствие влияния различных факторов. Сказанное относится к таким процессам и явлениям, как получение новых материалов и изменение свойств существующих, контроль качества материалов при их производстве, разрушение материалов, уплотнение сыпучих материалов и сред (в строительной отрасли), обогащение и разделение сыпучих материалов по их свойствам и т.д. Существующие разработки не всегда позволяют качественно и быстро определять упругие свойства материалов, особенно в полевых условиях при отсутствии лабораторной базы и в подавляющем большинстве характеризуются низкой точностью. Поэтому проблема разработки эффективного мобильного способа определения упругих свойств материалов остается актуальной.
Определение упругих свойств материалов, в частности модуля упругости, может производиться путем статического сжатия или растяжения соответствующих образцов на прессах или разрывных машинах. В ходе проведения таких испытаний определяются деформации при соответствующих нагрузках и рассчитывается модуль упругости материала (Сопротивление материалов / Под ред. Писаренко Г.С. - Киев: Вища шк., 1986, - с.108; Экспериментальные методы исследования деформаций и напряжений. Справочное пособие. Касаткин Б.С. и др. - Киев: Наукова думка, 1981, - с.108).
Недостатком таких испытаний является необходимость наличия сложного испытательного оборудования и соответствующих лабораторий, а также необходимость изготовления соответствующих образцов.
Более простыми и удобными являются ударные способы определения физико-механических свойств материалов. Согласно им по образцу исследуемого материала наносится удар индентором, например стальным шариком, и по параметрам ударного взаимодействия судят о физико-механических свойствах материала, а именно упругости, пластичности, прочности, твердости и др. При этом в качестве параметров ударного взаимодействия используют высоту отскока индентора, скорости падения и отскока индентора, продолжительность удара и целый ряд других параметров.
В экспериментальной части наиболее близкими к предлагаемому способу определения модуля упругости материала являются способ определения динамической твердости (а.с. СССР №1307295, кл. G 01 N 3/48, 1987) и способ контроля рабочих свойств акробатических дорожек (патент РФ №2020989, кл. G 01 N 3/52, 1994). В данных способах наносят удар индентором по исследуемому объекту и определяют время между первым и вторым соударениями индентора с исследуемым объектом, которое характеризует высоту отскока, и длительность первого соударения. Однако данные способы не позволяют на основе полученной информации оценить модуль упругости материала исследуемого объекта.
Известен способ определения упругих свойств твердых материалов, согласно которому на поверхность образца исследуемого материала с заданной высоты сбрасывают индентор, например стальной шарик, измеряют высоту отскока шарика и по высоте отскока судят об упругих свойствах исследуемого материала (Материалы Всесоюзного научно-исследовательского геологического института. Геофизика, сб.12. - М.: Госгеолиздат, 1948, - с.62-71; а.с. СССР №59701). Недостатком способа является низкая достоверность, так как однозначно оценить упругие свойства исследуемого материала только по высоте отскока индентора практически невозможно. Объясняется это следующим.
В первую очередь высота отскока (или что то же самое при условии неучета аэродинамических сопротивлений движению при свободном отскоке и падении индентора время между первым и вторым соударениями индентора с образцом исследуемого материала) характеризует потери энергии удара на этапе контактного взаимодействия индентора с опорной поверхностью, которой является исследуемый образец. В частности, эти потери энергии могут быть объяснены возникающими в месте контакта пластическими деформациями, рассеянием энергии при упругих деформациях (внутреннее трение в материале), смятием или разрушением микронеровностей в зоне контакта и еще рядом факторов.
Таким образом, например, у материалов, имеющих близкие модули упругости, но различные пластические свойства, при ударе индентора возникают неодинаковые пластические деформации, сопровождаемые разными потерями энергии удара, а следовательно, высота отскока индентора оказывается различной. Из вышесказанного следует, что по высоте отскока индентора оценить упругие свойства материала можно только сложным косвенным способом, если известна взаимосвязь упругих свойств материала с факторами, характеризующими потери энергии на этапе контактного взаимодействия индентора с опорной поверхностью исследуемого образца. Поэтому для повышения достоверности способа необходимо использовать дополнительные параметры ударного взаимодействия, которые могут характеризовать упругие свойства материала более достоверно и точно. Таким параметром, например, может являться время удара.
Наиболее точным и близким к предлагаемому способу является способ определения модуля нормальной упругости (а.с. №1497491, кл. G 01 N 3/30, 1989), взятый за прототип, в котором на образец исследуемого материала воздействуют свободно падающим индентором шарообразной формы с известными свойствами, измеряют время между первым и вторым соударениями индентора с образцом исследуемого материала, кроме этого, дополнительно измеряют диаметр отпечатка индентора и на основе полученной информации рассчитывают модуль упругости исследуемого материала по математической формуле.
Однако данный способ обладает существенными недостатками, основными из которых являются невысокая достоверность, ограниченная область применения и сложность практической реализации. Объясняется это следующим.
Дополнительный параметр, в качестве которого предлагается использовать диаметр отпечатка индентора, в первую очередь характеризует не упругие, а пластические свойства материала, так как исследуются остаточные (пластические) деформации, возникающие вследствие ударного взаимодействия индентора с опорной поверхностью образца исследуемого материала. Таким образом, используется сложная косвенная взаимосвязь искомого параметра (модуля упругости материала) с измеряемыми величинами - временем между первым и вторым соударениями индентора с образцом исследуемого материала и диаметром отпечатка индентора. Как уже отмечалось выше, у материалов, имеющих близкие модули упругости, но различные пластические свойства при ударе индентора возникают неодинаковые пластические деформации и отпечатки индентора различные. Кроме того, пластические свойства материалов могут изменяться при различных видах обработки материалов. Например, при закалке стали существенно изменяется ее пластичность, хотя модуль упругости остается почти неизменным. Поэтому говорить о высокой достоверности данного способа на наш взгляд не всегда корректно.
Другим существенным недостатком прототипа является ограниченная область применения способа, так как он может быть реализован применительно к пластичным материалам. У хрупких материалов в зоне контакта возникают практически только упругие деформации, которые исчезают после снятия нагрузки. С другой стороны круг таких материалов достаточно широк, к ним относятся, например, каменные материалы (рудные и нерудные), чугуны, легированные закаленные стали и др.
Говоря о сложности практической реализации способа, следует отметить, что измерение времени между первым и вторым соударениями индентора с образцом исследуемого материала и измерение диаметра отпечатка индентора можно осуществить только различными методами, требующими применения оборудования различного принципа действия, что ведет к усложнению практической реализации способа.
Цель изобретения - повышение достоверности, расширение области применения и упрощение способа определения модуля упругости материала за счет дополнительного измерения времени удара индентора с образцом исследуемого материала и расчета модуля упругости исследуемого материала образца с помощью расчетной упруговязкой модели с нелинейным упругим элементом с использованием экспериментально найденных значений времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала.
Поставленная цель достигается тем, что дополнительно измеряют время удара индентора с образцом исследуемого материала, расчет модуля упругости выполняют с помощью расчетной упруговязкой модели с нелинейным упругим элементом с использованием экспериментально найденных значений времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала, для чего заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной упруговязкой моделью с нелинейным упругим элементом, задают предварительное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, при заданном предварительном значении коэффициента жесткости упругого элемента расчетной упруговязкой модели рассчитывают время между первым и вторым соударениями расчетной упруговязкой модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента вязкости вязкого элемента расчетной упруговязкой модели, при котором значение времени между первым и вторым соударениями расчетной упруговязкой модели совпадает с измеренным значением времени между первым и вторым соударениями индентора с образцом исследуемого материала, при выбранном численном значении коэффициента вязкости вязкого элемента расчетной упруговязкой модели рассчитывают время удара расчетной упруговязкой модели, подбирая при этом численное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента расчетной упруговязкой модели, при котором время удара расчетной упруговязкой модели совпадает с измеренным временем удара индентора.
Анализ уровня техники показал наличие новизны в предложенной совокупности новых признаков, а именно:
- дополнительно измеряют время удара индентора с образцом исследуемого материала,
- расчет модуля упругости выполняют с помощью расчетной упруговязкой модели с нелинейным упругим элементом с использованием экспериментально найденных значений времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала;
- заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной упруговязкой моделью с нелинейным упругим элементом;
- задают предварительное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, при заданном предварительном значении коэффициента жесткости упругого элемента расчетной упруговязкой модели рассчитывают время между первым и вторым соударениями расчетной упруговязкой модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента вязкости вязкого элемента расчетной упруговязкой модели, при котором значение времени между первым и вторым соударениями расчетной упруговязкой модели совпадает с измеренным значением времени между первым и вторым соударениями индентора с образцом исследуемого материала;
- при выбранном численном значении коэффициента вязкости вязкого элемента расчетной упруговязкой модели рассчитывают время удара расчетной упруговязкой модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента расчетной упруговязкой модели, при котором время удара расчетной упруговязкой модели совпадает с измеренным временем удара индентора.
Рассмотрим влияние отличительных признаков на достижение технического результата. Для повышения достоверности способа необходимо измерение дополнительных параметров ударного взаимодействия индентора с образцом исследуемого материала и более совершенное математическое описание рассматриваемого ударного процесса.
В заявляемом способе использование в качестве дополнительного параметра измерения времени удара индентора с образцом исследуемого материала наиболее целесообразно, так как он непосредственно связан с упругими свойствами соударяющихся тел. Чем выше модуль упругости материала, тем меньше величина упругих деформаций, возникающих при ударе, следовательно, меньше время удара. Аналогичная картина наблюдается в колебательных системах. Чем выше жесткость (упругость) колебательной системы, тем меньше амплитуда и больше частота собственных колебаний. Кроме того, выбранный параметр позволяет включить в область исследований значительно большее количество разнообразных материалов от упругопластичных до абсолютно упругих (хрупких). Исключением тут могут являться только очень пластичные материалы, для которых отскок индентора практически невозможен. Но этот недостаток характерен для любого ударного способа, предполагающего отскок индентора. Таким образом, данная операция позволяет повысить достоверность способа и расширить его область применения и является его неотъемлемой частью.
Для моделирования процесса на компьютере и осуществления расчетов необходима разработка и использование математической модели ударного взаимодействия индентора с исследуемым образцом материала. Необходимость моделирования рассматриваемого процесса объясняется тем, что модуль упругости материала нельзя измерить непосредственно в ходе эксперимента. Это параметр, к которому можно прийти только расчетным путем на основе исходных данных о динамике ударного взаимодействия индентора с исследуемым образцом материала. Разработка математической модели процесса потребовала проведения дополнительных теоретических исследований.
Используемая расчетная модель должна обеспечивать адекватность динамики движения и взаимодействия индентора с образцом исследуемого материала при математическом моделировании процесса. Критериями адекватности согласно заявляемому способу были приняты время между первым и вторым соударениями индентора с образцом исследуемого материала и время удара.
Время между первым и вторым соударениями индентора с образцом исследуемого материала характеризует высоту отскока индентора, если не принимать во внимание силы аэродинамических сопротивлений, возникающих при движении индентора в воздухе. Применительно к рассматриваемому случаю это вполне допустимо, так как при незначительных скоростях движения силы аэродинамических сопротивлений несоизмеримо малы по сравнению с собственным весом, например, стального индентора. Высота отскока индентора характеризует потери энергии при ударе на этапе контактного взаимодействия индентора с опорной поверхностью, которой является образец исследуемого материала. Эти потери энергии могут объясняться различными причинами, например возникающими в месте контакта пластическим деформациями, рассеянием энергии при упругих деформациях (внутреннее трение в материале), смятием или разрушением микронеровностей в зоне контакта и еще рядом факторов. Для того, чтобы обеспечить адекватность расчетной модели по высоте отскока, т.е. по потерям энергии, она должна иметь соответствующий элемент. При этом нет необходимости устанавливать и учитывать конкретные причины, вызвавшие потери энергии при ударе. В нашем случае достаточно оценить и учесть совокупные потери энергии, в этом случае отскок расчетной модели после удара будет соответствовать экспериментально определенной величине. Для этой цели нами использован наиболее простой и широко распространенный линейный вязкий элемент, сила сопротивления которого пропорциональна скорости деформации (Сопротивление материалов / Под ред. Писаренко Г.С. - Киев: Вища шк., 1986, - с.604; Лапшин В.Л., Байбородин Б.А. Аналитическое моделирование процесса разделения руд на вибродеке. - Иркутск: Изд-во Иркутск. гос. техн. ун-та, 1997, - с.24). Изменяя численное значение коэффициента вязкости вязкого элемента расчетной модели, можно регулировать потери энергии при деформации и, следовательно, ее высоту отскока.
Время удара связано с упругими свойствами взаимодействующих тел (сферическое тело-плоскость). Задача о сдавливании сферических тел была решена Г. Герцем еще в 1881 г. (Тимошенко С.П. Теория упругости. - Л.-М.: ОМТИ, 1937, - с.451). Им был предложен нелинейный упругий элемент, который позволяет рассчитать деформации при взаимодействии сферических тел в зависимости от их модулей упругости. Последующие практические исследования подтвердили достоверность предложенной модели. Поэтому в качестве упругого элемента расчетной модели нами выбран нелинейный упругий элемент Г.Герца. Он позволяет обеспечить адекватность модели по времени удара путем подбора численного значения коэффициента жесткости упругого элемента модели. При известном значении коэффициента жесткости упругого элемента расчетной упруговязкой модели для расчета модуля упругости исследуемого материала образца предлагается расчетная формула.
Таким образом, использование для математического описания процесса ударного взаимодействия индентора с образцом исследуемого материала расчетной упруговязкой модели с нелинейным упругим элементом, оценка потерь энергии при ударе по времени между первым и вторым соударениями индентора с образцом исследуемого материала путем подбора численного значения коэффициента вязкости вязкого элемента расчетной упруговязкой модели и оценка модуля упругости исследуемого материала образца по численному значению коэффициента жесткости упругого элемента расчетной упруговязкой модели, которое рассчитывается по времени удара индентора с образцом исследуемого материала путем подбора численного значения коэффициента жесткости упругого элемента расчетной упруговязкой модели являются неотъемлемыми операциями способа, позволяющими на основе исходных экспериментальных данных рассчитать искомый модуль упругости исследуемого материала образца с более высокой достоверностью.
Упрощение практической реализации способа достигается тем, что в экспериментальной части способа измеряются только временные интервалы: время между первым и вторым соударениями индентора с образцом исследуемого материала и время удара. Это можно осуществить одним и тем же методом, не требующим применения оборудования различного принципа действия, что характерно для прототипа.
Дополнительный поиск известных решений с признаками, совпадающими с отличительными от прототипа признаками заявляемого способа, не выявил влияния существенных признаков на достижение поставленного технического результата. Поэтому заявляемое изобретение соответствует критерию "изобретательский уровень".
Сущность изобретения поясняется чертежами, где на фиг.1 изображена схема расчетной упруговязкой модели с нелинейным упругим элементом; на фиг.2 - схема экспериментальной установки. На чертежах приняты следующие обозначения: m - масса индентора; 1 - сферический индентор; 2 - образец исследуемого материала; 3 - вязкий элемент расчетной упруговязкой модели; 4 - упругий элемент расчетной упруговязкой модели.
Заявляемый способ осуществляется следующим образом. В процессе эксперимента свободно падающим индентором шарообразной формы с известными свойствами наносится удар по образцу исследуемого материала и фиксируются параметры ударного взаимодействия системы: время удара и время между первым и вторым соударениями индентора с образцом исследуемого материала (высота отскока). Далее выполняется расчет с помощью разработанной программы. Для этого используется расчетная упруговязкая модель с нелинейным упругим элементом.
Рассмотрим расчетную упруговязкую модель рассматриваемого процесса, схема которой представлена на фиг.1. Данная модель позволяет описать динамику процесса ударного взаимодействия индентора шарообразной формы с образцом исследуемого материала. Дифференциальное уравнение движения центра тяжести индентора шарообразной формы на этапе ударного взаимодействия имеет вид

где: m - масса индентора; Р - вес индентора; К - коэффициент жесткости упругого элемента расчетной упруговязкой модели; С - коэффициент вязкости вязкого элемента расчетной упруговязкой модели;  - ускорение центра тяжести индентора;
- ускорение центра тяжести индентора;  - скорость деформации; у - величина деформации. Сила нормальной реакции индентора на поверхность исследуемого материала определяется из выражения
- скорость деформации; у - величина деформации. Сила нормальной реакции индентора на поверхность исследуемого материала определяется из выражения

Коэффициент жесткости упругого элемента расчетной упруговязкой модели К связан со свойствами и параметрами индентора и свойствами исследуемого образца материала и рассчитывается по формуле (Тимошенко С.П. Теория упругости. - Л. - М.: ОМТИ, 1937, - с.451)

где: R1, R2 - радиусы кривизны индентора шарообразной формы и поверхности образца исследуемого материала; E1, Е2 - модули упругости (модули Юнга) соответственно материала индентора и исследуемого образца;  1,
1,  2 - коэффициенты Пуассона соответственно материала индентора и исследуемого образца.
2 - коэффициенты Пуассона соответственно материала индентора и исследуемого образца.
Последовательность определения модуля упругости материала исследуемого образца выглядит следующим образом.
Задаются исходные данные расчетной упруговязкой модели m, Р, С, R1, R2, E1, Е2,  1,
1,  2 и рассчитывается начальная скорость индентора в момент удара
2 и рассчитывается начальная скорость индентора в момент удара  (Н - исходная высота падения индентора; g - ускорение свободного падения). Если поверхность исследуемого образца материала является плоской, то вышеприведенные формулы также применимы. В этом случае достаточно принять радиус кривизны поверхности исследуемого образца R2 намного большим радиуса кривизны индентора R 1 (например R2=1000 м). Погрешность расчета в этом случае ничтожна мала. Для С, Е2 принимаются ориентировочные значения (например С=0, Е1=Е2 ). Коэффициент Пуассона материала исследуемого образца, как показали предварительные расчеты, оказывает очень незначительное влияние на конечный результат, даже если его варьировать в широких пределах (например,
(Н - исходная высота падения индентора; g - ускорение свободного падения). Если поверхность исследуемого образца материала является плоской, то вышеприведенные формулы также применимы. В этом случае достаточно принять радиус кривизны поверхности исследуемого образца R2 намного большим радиуса кривизны индентора R 1 (например R2=1000 м). Погрешность расчета в этом случае ничтожна мала. Для С, Е2 принимаются ориентировочные значения (например С=0, Е1=Е2 ). Коэффициент Пуассона материала исследуемого образца, как показали предварительные расчеты, оказывает очень незначительное влияние на конечный результат, даже если его варьировать в широких пределах (например,  2=0,15÷0,4). Поэтому, в случае, если коэффициент Пуассона материала исследуемого образца также является неизвестной величиной, вполне допустимо принять ориентировочное значение (например
2=0,15÷0,4). Поэтому, в случае, если коэффициент Пуассона материала исследуемого образца также является неизвестной величиной, вполне допустимо принять ориентировочное значение (например  1=
1= 2).
2).
Далее выполняется расчет с помощью разработанной программы. На базе рассмотренной математической модели был разработан алгоритм и исследовательская программа в оболочке Visual Basic. Для решения уравнения (1) использовался численный метод Рунге-Кутта. Программа позволяет рассчитать параметры ударного взаимодействия системы: силу нормальной реакции, время удара, величину деформации, высоту отскока индентора от поверхности. Расчет выполняется пошагово с заданным шагом dt. В результате расчета определяется момент отрыва (отскока) индентора от исследуемой поверхности, которому соответствует выполнение условия N=0 (выражение (2)) и время удара  , где n - количество шагов вычисления на этапе ударного взаимодействия системы). Зная начальную скорость в момент отскока
, где n - количество шагов вычисления на этапе ударного взаимодействия системы). Зная начальную скорость в момент отскока  (из расчета по программе) определяется высота отскока модели
(из расчета по программе) определяется высота отскока модели  (g=9,8 м/c2) и время между первым и вторым соударениями индентора с образцом исследуемого материала
(g=9,8 м/c2) и время между первым и вторым соударениями индентора с образцом исследуемого материала  (время полета индентора после отскока).
(время полета индентора после отскока).
На следующем этапе выполняется сравнение расчетных параметров с экспериментально найденными значениями времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала.
Для обеспечения адекватности расчетной упруговязкой модели по потерям энергии при ударе варьируют численное значение коэффициента вязкости С вязкого элемента 3 расчетной упруговязкой модели (фиг.1), добиваясь совпадения расчетного и экспериментального значений времени между первым и вторым соударениями индентора с образцом исследуемого материала. После этого при найденном значении С варьируют численное значение коэффициента жесткости К упругого элемента 4 расчетной упруговязкой модели (фиг.1) путем изменения численного значения модуля упругости (модуля Юнга) материала исследуемого образца Е2 добиваясь совпадения расчетного и экспериментального значений времени удара индентора с образцом исследуемого материала. Таким образом, в результате расчета при известных параметрах индентора подбирается такое значение модуля упругости материала исследуемого образца, при котором динамика процесса ударного взаимодействия на расчетной модели соответствует экспериментальным данным.
Пример.
Для проверки работоспособности заявляемого способа были проведены специальные эксперименты с помощью разработанной экспериментальной установки, схема которой представлена на фиг.2. Установка состоит из генератора высокочастотного сигнала, соединенного гибким проводником с образцом исследуемого материала, и счетчика импульсов, соединенного гибким проводником с индентором шарообразной формы. В качестве индентора использовался стальной шарик диаметром d=12 мм и массой m=7 г (R1 =6 мм, Е1=200000 МПа,  1=0,27). Высота падения индентора варьировалась в пределах Н=20÷60 мм. В качестве исследуемого материала использовались образцы из стали 45, дюралюминия Д16, чугуна СЧ21-40, титана ВТ 14.
1=0,27). Высота падения индентора варьировалась в пределах Н=20÷60 мм. В качестве исследуемого материала использовались образцы из стали 45, дюралюминия Д16, чугуна СЧ21-40, титана ВТ 14.
Установка работает следующим образом. При возникновении контакта индентора с поверхностью исследуемого образца высокочастотный сигнал начинает поступать на счетчик импульсов. Зная частоту сигнала генератора и количество импульсов, поступивших за период контакта, определяют время удара индентора. Аналогичным образом определяют время между первым и вторым соударениями, как период времени между разрывом контакта и повторным его возобновлением при втором ударе.
В качестве примера в таблице приводятся результаты испытаний для высоты падения индентора Н=24 мм.
Как видно из приведенных данных (см. таблицу), относительная погрешность определения модуля упругости исследуемых образцов не превышала 3% как в приведенных, так и в остальных опытах. Высота падения индентора (в выбранном диапазоне) практически не сказывалась на точности конечного результата.
Результаты экспериментальных исследований
| Образец | Модуль упругости фактич., МПа | Коэфф. Пуассона | Модуль упругости расчетн., МПа | Относит. погрешн. расчета, % | Время удара ×10 -5 с | Время полета при отскоке, с | Высота отскока, мм |
| Дюралюминий Д16 | 71000 | 0,31 | 69700 | 1,83 | 6,53 | 0,107 | 14 |
| Чугун СЧ21-40 | 85000 | 0,25 | 85900 | 1,1 | 6,06 | 0,099 | 12 |
| Титан ВТ14 | 115000 | 0,3 | 116500 | 1,3 | 5,74 | 0,128 | 20 |
| Сталь 45 | 200000 | 0,27 | 195500 | 2,25 | 5,05 | 0,131 | 21 |
Кроме этого, были выполнены расчеты для случая, когда коэффициент Пуассона исследуемого материала не известен. Для этого при расчетах во всех опытах принимались не фактические значения коэффициента Пуассона, а для всех материалов использовалось среднее значение  2=0,275. В этих случаях погрешность расчета несущественно увеличивалась (до 3-5%).
2=0,275. В этих случаях погрешность расчета несущественно увеличивалась (до 3-5%).
Указанные погрешности в первую очередь связаны с установкой, так как основной целью эксперимента являлась принципиальная проверка работоспособности заявляемого способа, тем не менее была достигнута достаточно высокая достоверность.
Следует отметить, что в установке использовался наиболее простой метод измерения времени удара и полета индентора, который предполагает электропроводность исследуемого материала. Для неэлектропроводных материалов (например, каменных) можно использовать другой метод измерения или покрывать их поверхность очень тонким слоем электропроводящего материала. При достаточно тонком слое это не окажет существенного влияния на достоверность конечного результата.
Следует также отметить, что результаты испытаний подтвердили низкую достоверность известных способов в случае, когда используется только один экспериментально найденный параметр ударного взаимодействия (время удара или время между первым и вторым соударениями индентора с образцом исследуемого материала). Как видно из приведенных данных, время между первым и вторым соударениями индентора с образцом исследуемого материала (высота отскока) у стали и титана отличаются незначительно, хотя модули упругости различаются существенным образом (см. таблицу). С другой стороны, у дюралюминия данный параметр больше, чем у чугуна, хотя модуль упругости у дюралюминия наименьший среди рассмотренных материалов.
Более логичная взаимосвязь прослеживается между временем удара и модулем упругости материала. Чем больше модуль упругости, тем меньше время удара. Однако данная взаимосвязь является явно не линейной и достаточно сложной. Это становится очевидным, если сравнить, например, дюралюминий с чугуном и дюралюминий со сталью. В первом случае при увеличении модуля упругости на 20% время удара уменьшается на 8%, во втором случае при увеличении модуля упругости почти на 200% время удара уменьшается всего на 23%.
Таким образом, результаты экспериментальных исследований показали, что только совместный учет как минимум двух параметров ударного взаимодействия (времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала) позволяет достичь более высокой достоверности способа определения модуля упругости материала ударным способом. При этом достигается расширение области применения способа, так как нет необходимости оценивать пластические деформации ударного взаимодействия, и обеспечивается упрощение способа, так как все измерения выполняются с помощью одного измерительного устройства, фиксирующего только временные интервалы.
ФОРМУЛА ИЗОБРЕТЕНИЯ
Способ определения модуля упругости материала, заключающийся в том, что на образец исследуемого материала воздействуют свободно падающим индентором шарообразной формы с известными свойствами и измеряют время между первым и вторым соударениями индентора с образцом исследуемого материала, отличающийся тем, что дополнительно измеряют время удара индентора с образцом исследуемого материала, расчет модуля упругости выполняют с помощью расчетной упруговязкой модели с нелинейным упругим элементом с использованием экспериментально найденных значений времени удара и времени между первым и вторым соударениями индентора с образцом исследуемого материала, для чего заменяют систему образец исследуемого материала - индентор на этапе контакта индентора с образцом исследуемого материала расчетной упруговязкой моделью с нелинейным упругим элементом, задают предварительное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, при заданном предварительном значении коэффициента жесткости упругого элемента расчетной упруговязкой модели рассчитывают время между первым и вторым соударениями расчетной упруговязкой модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента вязкости вязкого элемента расчетной упруговязкой модели, при котором значение времени между первым и вторым соударениями расчетной упруговязкой модели совпадает с измеренным значением времени между первым и вторым соударениями индентора с образцом исследуемого материала, при выбранном численном значении коэффициента вязкости вязкого элемента расчетной упруговязкой модели рассчитывают время удара расчетной упруговязкой модели с образцом исследуемого материала, подбирая при этом численное значение коэффициента жесткости упругого элемента расчетной упруговязкой модели, а об искомом модуле упругости исследуемого материала образца судят по численному значению коэффициента жесткости упругого элемента расчетной упруговязкой модели, при котором время удара расчетной упруговязкой модели совпадает с измеренным временем удара индентора.
www.freepatent.ru
Способ определения модуля упругости материала
Изобретение касается испытаний конструкционных материалов и используется для определения модуля упругости металлов и их сплавов при различных температурах. Цель изобретения - повьппение точности. Это достигается за счет исключения влияния внутренних напряжений в образце на частоту собственных колебаний путем обработки поверхности резанием на режиме , минимизирующем изменение собственной частоты продольных колебаний , и последующего отжига, температуру и длительность которого определяют из условия получения наибольшего изменения частоты после отжига при минимальной температуре. Изготовленный образец обрабатывают резанием на нескольких режимах для определения режима, меньше всего изменяющего частоту . На этом режиме обрабатывают поверхность партии образцов, для нахождения режима отжига, дающего наибольшее изменение частоты. Образец, подвергнутый отжигу на этом режиме, используют для определения модуля упругости при данной температуре по его частоте и линейным размерам. 1 табл. с S сл о :о ел ND 00 -4j
СОЮЗ СОВЕТСКИХ
СОЦИАЛИСТИЧЕСКИХ
РЕСПУБЛИК ()9) SU (II) (50 4 С 01 И 3/32
ГОСУДАРСТВЕННЫЙ НОМИТЕТ СССР
ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ
Ь .
ОПИСАНИЕ ИЗОБРЕТЕНИЯ::3.
К ABTOPCHOMY СВИДЕТЕЛЬСТВУ (21) 3930626/25-28 (22) 05.06.85 (46) 07.03.87. Бюл. 119 9 (72) П.К.Янышев и А.П.Янышев (53) 531.781.2(088.8) (56) Авторское свидетельство СССР
9 807130, кл. G 01 N 3/32, 1979.
Авторское свидетельство СССР
119 244681, кл. G 01 N 11/16, 1968. (54) СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА (57) Изобретение касается испытаний конструкционных материалов и исполь". зуется для определения модуля упругости металлов и их сплавов при различных температурах. Цель изобретения — повышение точности. Это достигается за счет исключения влияния внутренних напряжений в образце на частоту собственных колебаний путем обработки поверхности резанием на режиме, минимизирующем изменение собственной частоты продольных колебаний, и последующего бтжига, температуру и длительность которого определяют из условия получения наибольшего изменения. частоты после отжига при минимальной температуре ° Изготовленный образец обрабатывают резанием на нескольких режимах для определения режима, меньше всего изменяющего частоту. На этом режиме обрабатывают поверхность партии образцов. для нахождения режима отжига, дающего наибольшее изменение частоты. Образец, подвергнутый отжигу на этом режиме, используют для определения модуля упругости при данной температуре по его частоте и линейным размерам. 1 табл.
1 295287
S, мм/об. и об/мин
560 900 1120 1400 1800 2240 2800
0,088 85,6
83,1 77,8
72,1
68,3
57,0 52,4
0,108 29,6 24,2 20,8 14,5 9,0 -0,8 -2,7
0,133 -65,0 -81,8 -91,2 -94,6 -101,3 -117,8 -143,9
Изобретение относится к области испытаний конструкционных материалов и может быть использовано при определении модулей упругости металлов и их сплавов. 5
Цель изобретения — повышение точности, Это достигается за счет исключения влияния внутренних напряжений в образце на частоту собственных колебаний путем обработки поверхности образца резанием на режиме, минимизирующем изменение собственной частоты продольных колебаний, и последующего
f5 отжига, температуру и длительность которого определяют из условия получения наибольшего изменения частоты после отжига при минимальной температуре.
Способ осуществляют следующим об20 разом.
Изготавливают стержневой образец из исследуемого материала, например, в форме цилиндра. Для этого образца подбирают режим резания, например то- 25 чения, который приводит к минимальному изменению частоты собственных колебаний после обработки. Для этого до обработки возбуждают в образце продольные колебания и измеряют их
На найденном режиме вновь проводят обработку поверхности образца и 45 измеряют частоту собственных колебаний после чистовой обработки.
Затем производится определение режима стабилизирующего отжига. Для этого изготавливают партию образцов 50 с поверхностью, обработанной резанием на найденном режиме, измеряют собственные частоты продольных колебаний этих образцов и подвергают образцы отжигу при различных значениях температуры отжига и нескольких длительностях их термообработки, после. чего вновь определяют их частоты собственных колебаний. За искомый режим частоту,, а затем. проводят обработку поверхности резанием на различных режимах, измеряя после каждого этапа обработки собственную частоту образца.
Процесс обработки конструкционных материалов резанием сопровождается как силовым, так и тепловым воздействием на обрабатываемую заготовку. Силовое воздействие вызывает образование сжимающих внутренних напряжений, а тепловое — растягивающих . Это позволяет подобрать чистовой режим обработки, при котором силовое и тепловое воздействия взаимно компенсируются, т.е. изменений в поверхностном слое не образуется. Так, для стали 40 такой режим составляет: t=0 12 мм/ст, S=0 108 мм/об„, v=46 м/мин, при этом увеличение скорости резания и подачи сопровождается уменьшением сжимающих внутренних напряжений, а глубины резания увеличением, которые можно оценить по приращению частот собственных колебаний заготовок после обработки
В таблице приведены данные для заготовок диаметром 6,4 мм. стабилизирующего отжига принимают такой, который дает наибольшее изменение собственной частоты колебаний.
Например, для стали 40 получены темо пература отжига 550 С и длительность
130 мин.
У образца, подвергнутого такому стабилизирующему отжигу, измеряют длину и частоту собственных продольных колебаний и по этим данным определяют модуль упругости материала.
Использование предлагаемого способа для определения модуля упругости металлов и их сплавов в широком температурном диапазоне позволяет повы1295287
Составитель Н.Тимошенко
Техред М.Ходанич Корректор М. Пожо
Редактор Е.Папп
Заказ 611/50 Тираж 777 Подписное
ВНИИПИ Государственного комитета СССР по делам изобретений и открытий
113035, Москва, Ж-35, Раушская наб., д .4/5
Производственно-полиграфическое предприятие,г.Ужгород,ул.Проектная,4 сить точность определения истинного модуля упругости конструкционного материала для данной температуры, так как это определение производится по частоте, которая является надежно воспроизводимой и по самому способу подготовки образца к эксперименту— наиболее стабильной для данного материала.
Формула изобретения
Способ определения модуля упругости материала, заключающийся в том, что в образце возбуждают продольные колебания на собственной частоте и измеряют эту частоту, о т л и ч а юшийся тем, что, с целью повышения точности, предварительно обраЬа5 тывают поверхность образца резанием на режиме, выбранном из условия, что-. бы изменение частоты собственных колебаний после обработки было минимальным, и проводят стабилизирующий отжиг образца, температуру и длительность которого выбирают из условия получения наибольшего приращения собственной частоты после отжига при минимальной температуре, обеспечивающей это приращение.



www.findpatent.ru
ОДМ 218.3.023-2012 Методические рекомендации по определению модуля упругости дорожной одежды с использованием статического жесткого штампа
|
ОДМ 218.3.023-2011 |
|
ОТРАСЛЕВОЙ ДОРОЖНЫЙ МЕТОДИЧЕСКИЙ ДОКУМЕНТ |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОПРЕДЕЛЕНИЮ МОДУЛЯ УПРУГОСТИ ДОРОЖНОЙ ОДЕЖДЫ С ИСПОЛЬЗОВАНИЕМ СТАТИЧЕСКОГО ЖЕСТКОГО ШТАМПА
ФЕДЕРАЛЬНОЕ ДОРОЖНОЕ АГЕНТСТВО (РОСАВТОДОР)
Москва 2012
Предисловие
1 РАЗРАБОТАН Обществом с ограниченной ответственностью «Инновационный технический центр».
2 ВНЕСЕН Управлением научно-технических исследований, информационного обеспечения и ценообразования Федерального дорожного агентства.
3 ИЗДАН на основании распоряжения Федерального дорожного агентства от 03.05.2012 № 245-р.
4 ИМЕЕТ РЕКОМЕНДАТЕЛЬНЫЙ ХАРАКТЕР.
5 ВВЕДЕН ВПЕРВЫЕ.
СОДЕРЖАНИЕ
ОДМ 218.3.023-2012
ОТРАСЛЕВОЙ ДОРОЖНЫЙ МЕТОДИЧЕСКИЙ ДОКУМЕНТ
|
Методические рекомендации по определению модуля упругости дорожной одежды с использованием статического жесткого штампа |
Настоящий отраслевой дорожный методический документ (далее - методический документ) устанавливает рекомендации по определению модуля упругости нежестких дорожных одежд с использованием жесткого штампа.
В настоящем методическом документе использованы нормативные ссылки на следующие документы:
ГОСТ 577-68 Индикаторы часового типа с ценой деления 0,01 мм. Технические условия.
В настоящем методическом документе применены следующие термины с соответствующими определениями:
3.1 обратимый прогиб (модуль упругости): Обобщающий критерий несущей способности (прочности) дорожной одежды.
3.2 нежесткая дорожная одежда: Дорожная одежда с асфальтобетонными слоями и слоями из минеральных материалов, как укрепленных органическими вяжущими, так и неукрепленных.
3.3 штамп: Круглая металлическая плита диаметром 300 мм и толщиной 25 мм.
Сущность метода заключается в определении обратимого прогиба нежесткой дорожной одежды, возникающего после снятия с нее статической нагрузки, приложенной через жесткий штамп.
4.1 Условия измерений
Измерения проводятся при температуре воздуха не ниже 5 °С, поддерживаемой в течение суток до начала проведения измерений, при этом материалы слоев дорожной одежды и фунты рабочего слоя должны находиться в незамерзшем состоянии.
Измерения рекомендуется проводить в соответствии с требованиями к условиям проведения измерений, указанными в паспорте на средство измерения и в соответствии с руководством по эксплуатации.
Поверхность испытуемой дорожной одежды непосредственно в месте проведения измерений должна быть чистой, без выступающих элементов и обеспечивать максимально возможное соприкосновение по всей площади штампа. Не допускается установка штампа над углублениями (выбоинами, на колее).
4.2 Используемое оборудование
Для проведения измерений используется следующее оборудование:
- штамп диаметром 300 мм и толщиной 25 мм;
- домкрат;
- насос с манометром, обеспечивающим измерение давления не менее 0,6 МПа;
- выдвижная штанга с отметкой и цилиндрическим уровнем, которая обеспечивает удаление оси опор штанги на (1500 ± 5) мм от центральной точки штампа. Отметкой на штанге указано требуемое удаление;
- индикатор часового типа с разрешающей способностью индикации значений измерения не менее 0,01 мм по ГОСТ 577-68;
- измерительная планка.
4.3 Подготовка к выполнению измерений
Общая схема установки прибора при проведении испытаний представлена на рисунке 1.
1 - несущий каркас выдвижной штанги; 2 - индикатор часового типа; 3 - измерительная планка; 4 - линейный подшипник; 5 - нагрузка от упора; 6 - центральная точка штампа; 7 - цоколь штампа с прорезью; 8 - опоры штанги (размер дан в метрах)
Рисунок 1 - Общая схема установки прибора при проведении измерений
Для установки прибора требуется упор. В качестве упора можно использовать груженый грузовой автомобиль (прибор устанавливается под заднюю раму), каток или соответствующий жесткий противовес. Масса упора должна обеспечивать задание максимальной нагрузки от штампа.
Штамп устанавливается на поверхность испытуемой дорожной одежды. В случае необходимости для устранения неровностей наносится слой сухого песка средней крупности или гипса. Затем на поверхность помещается штамп (поворачиванием или постукиванием по нему). В случае применения гипсовой кашицы, поверхность основания грузовой плиты смазывается маслом. Кашица, выдавленная сбоку, удаляется до затвердевания. Проведение измерений начинается после того, как схватится гипсовая подложка.
В центр штампа устанавливается домкрат, предварительно очищенный от пыли и песка. Если домкрат засорен, достигнуть в нем нужного усилия будет невозможно.
К домкрату подключается насос.
При помощи цилиндрического уровня штанга устанавливается в горизонтальное положение. Одновременно с этим в центр прорези в цоколе штампа с помощью линейного подшипника с индикатором приставляется измерительная планка. При этом необходимо следить за тем, чтобы измерительная планка беспрепятственно входила в прорезь в цоколе штампа и размещалась в его центре.
Индикатор устанавливается в вертикальное положение.
Расстояние между опорами штанги и опорной поверхностью упора должно составлять от 1,5 до 1,25 м.
С помощью насоса в домкрате создается давление, равное 0,02 МПа. Домкрат при этом должен располагаться под прямым углом к поверхности штампа.
Выждав 1 - 2 мин, выставляются показания индикатора на ноль и проводится испытание.
4.4 Порядок проведения измерений
С помощью насоса в домкрате создается давление, равное 0,6 МПа. Нагрузка на дорожную одежду при таком давлении выдерживается до тех пор, пока скорость осадки штампа не станет менее 0,03 мм/мин, и записываются показания индикатора. После этого давление в домкрате сбрасывается до 0,02 МПа и остается таким, чтобы штамп и домкрат не сместились в сторону. В таком состоянии штамп остается до прекращения упругого восстановления деформации, показания индикатора записываются.
Разница показаний индикатора при максимальном давлении и после сброса давления является величиной обратимого прогиба.
4.5 Обработка результатов измерений
Полученные результаты прогибов фиксируются в соответствующем журнале. Фактический обратимый прогиб определяется по формуле
где l - фактическая величина обратимого прогиба, мм;
lд - величина осадки штампа под нагрузкой, мм;
lс - величина осадки штампа после снятия нагрузки, мм.
Модуль упругости Еу, МПа, вычисляется по формуле
|
(2) |
где р - удельная нагрузка, МН/м2, под действием которой получена обратимая деформация, равная l, мм;
D - диаметр жесткого штампа, мм;
μ - коэффициент Пуассона, среднее значение которого при вычислении общего модуля упругости слоистой конструкции принимается равным 0,3;
- поправочный коэффициент при испытании жестким штампом.
|
Ключевые слова: жесткий штамп, дорожная одежда, обратимый прогиб |
Руководитель организации разработчика ООО «Инновационный технический центр»
|
Генеральный директор |
__________________ подпись |
Д.И. Оверин |
files.stroyinf.ru
Способ определения модуля упругости материалов
Изобретение относится к исследованию упругих свойств материалов. Цель изобретения - повьшение точности при исследовании материалов с большим внутренним трением. Для этого в образце в виде балки прямоугольного поперечного сечения, образованной подложкой с нанесенными на нее с двух противоположных сторон, перпендикулярных плоскости колебаний, слоями исследуемого материала возбуждают резонансные нагибные колебания и измеряют распределение амплитуды скорости на поверхности образца. Возбуждают резонансные изгибные колебания подложки, уровень которых устанавливают из условия равенства амплитуды деформации на поверхности подложки амплитуде деформаций на поверхности подложки при колебаниях образца, и измеряют распределение амплитуд деформации и скорости на поверхности подложки. Модуль упругости исследуемого материала рассчитывают по измеренным величинам с учетом плотностей исследуемого материала и подложки и толщин слоев материала и подложки. Расчетное соотношение получено из условия баланса потенциальной и кинетической энергий деформирования. Это повышает точность определения модуля упругости за счет исключения влияния внутреннего трения. с ® (Л
СОЮЗ СОВЕТСНИХ
СОЦИАЛИСТИЧЕСКИХ
РЕСПУБЛИК
16891 А1 (!9) (И) (51)4 G 01 N 3 32
ОПИСАНИЕ ИЗОБРЕТЕНИЯ
К А BTOPCHOMV СВИДЕТЕЛЬСТВУ
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР
ПО ДЕЛАМ ИЗОБРЕТЕНИЙ И ОТКРЫТИЙ (21) 4115356/25-28 (22) 10.09.86 (46) 15.08.88. Бюл. У 30 (75) С.В.Буйлов, С.В.Дятченко и А.П.Яковлев (53) 534.282:620. 178(088.8) (56) Дж. Ферри. Вязкоупругие свойства полимеров. M.: ИЛ, !963, с. 159. (54) СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛОВ (57) Изобретение относится к исследованию упругих свойств материалов.
Цель изобретения — повышение точности при исследовании материалов с большим внутренним трением. Для этого в образце в виде балки прямоугольного поперечного сечения, образованной подложкой с нанесенными на нее с двух противоположных сторон, перпендику-. лярных плоскости колебаний, слоями исследуемого материала возбуждают резонансные изгибные колебания и измеряют распределение амплитуды скорости на поверхности образца. Возбуждают резонансные изгибные колебания подложки, уровень которых устанавливают иэ условия равенства амплитуды деформации на поверхности подложки амппитуде деформаций на поверхности подложки при колебаниях образца, и измеряют распределение амплитуд деформации и скорости на поверхности подложки. Модуль упругости исследуемого материала рассчитывают по измеренным величинам с учетом плотностей исследуемого материала и подложки и толщин слоев материала и подложки. щ с
Расчетное соотношение получено из условия баланса потенциальной и кинетической энергий деформироеения. Это повышает точность определения модуля упругости за счет исключения влияния Я внутреннего трения.
1416891
Изобретение относится к исследованию прочностных свойств материалов, а именно к способам определения модуля упругости материалов, преимущественно вибродемпфирующих покрытий.
Цель изобретения — повышение точности при исследовании материалов с большим внутренним трением.
Способ осуществляют следующим образом.
Возбуждают изгибные резонансные колебания в образце в виде балки прямоугольного сечения, образованной подложкой с нанесенными на нее с двух 15 противоположных сторон, перпендикулярных плоскости колебаний, слоями исследуемого материала, измеряют распределение амплитуды скорости колебания образца, возбуждают изгиб- 20 ные резонансные колебания подложки, уровень которых устанавливают из условия равенства деформации на поверхности подложки амплитуде деформации на поверхности подложки при коле- 25 баниях со слоями исследуемого материала, и измеряют распределение амплитуд деформации и скорости на поверхности подложки. Модуль E упругости исследуемого материала определяют из соотношения
) jv Ь (-р +рп п)- -ч2Ьр Jdx
Е-.2 — ——
Ф
j Pt„+2 t2 /t+4/З.t4/t21 2dx () где Ь вЂ” ширина образца; — плотности исследуемого матеп)с риала и подложки соответственно; 40
t > t — толщина слоя исследуемого материала и подложки соответственно; с,v — амплитуды скорости колебаний составного образца и подлож- 45 ки соответственно; „ - амплитуда деформации на поверхности покрытия;
1 — длина образца.
По данному способу модуль упругос-50 ти материала определяют из условия баланса кинетической и потенциальной энергий, определенных по измеренным амплитудным значениям скоростей и деформаций.
При выводе соотношения для определения модуля упругости учитывается, что максимальная кинетическая энергия W составного образца равна с) =)),+w„=jv ü(-ðñ ö ñ„)4õ, (2) о где И„, „ — максимальные кинетические энергии слоев исследуемого материала и подложки соответственно при колебаниях образца, а максимальная кинетическая энергия W колебаний подложки без покрытия равна
W=$> ЦсЬ4х, (3)
0 где v — амплитудное значение скорости подложки, колеблющейся беэ покрытия.
Принимается, что рассеяние энергии при колебаниях не влияет на форму колебаний. При условии равенства амплитуд деформаций на поверхности подложки со слоями исследуемого материала потенциальная энергия подложки в образце равна потенциальной энергии подложки без покрытия.
Амплитуду деформации „ на поверхности подложки при колебаниях образца определяют по результатам замера амплитуды деформации на поверхности образца
t (4) где " — амплитуда деформации на пои верхности образца.
Так как при установившихся резонансных колебаниях максимальная кинетическая энергия равна максимальной потенциальной энергии колебаний образца, то потенциальная энергия У,„ слоев исследуемого материала может быть выражена через значения кинетических энергий, определенных по замеренным значениям скоростей
U и™ и+Ы1™ (5) а также через значения деформаций
V =Е (t +2->-+- ->-) 2Ьйх.
3 (2 а о (6)
Приравнивая (4) и (5), получают выражение для модуля упругости
) fv2Ь(-yt+ у -t„) — -v21Ч)dx
1 1
О
Е- — — — — ——
С t
Предлагаемый способ повышает точность исследования слоев с большим декрементом затухания, так как основан на условии баланса кинетической и потенциальной энергий колебаний
1416891 и, таким образом, внутреннее трение материала не влияет на определяемую величину модуля упругости.
v (х), амплитуды скорости колебаний составного образца и подложки соответственно; амплитуда деформации на поверхности подложки; длина образца.
Составитель И.Ямщиков
Редактор М.Петрова . Техред М.Ходанич Корректор О.Кравцова
Заказ 4060/42 Тираж 847 Подписное
ВНИИПИ Государственного комитета СССР по делам изобретений и открытий
113035, Москва, Ж-35, Раушская наб., д, 4/5
Производственно-полиграфическое предприятие, г. Ужгород, ул. Проектная, 4
Формула изобретения
Способ определения модуля упругости материалов, по которому возбуждают изгибные резонансные колебания образца в виде балки прямоугольного поперечного сечения, образованной подложкой с нанесенными на нее с двух противоположных сторон, перпендикулярных плоскостей колебаний, слоями исследуемого материала, определяют параметры колебаний образца, по которым определяют модуль упругости исследуемого материала, о т л и ч а ю щ и йс я тем, что, с целью повышения точности при исследовании материалов с большим внутренним трением, возбуждают изгибные резонансные колебания подложки, уровень возбуждения образца и подложки устанавливают из условия равенства амплитуд деформаций на 2б поверхности подложки со слоями исследуемого материала и без них, измеряют распределение по длине амплитуды деформации на поверхности подложки и распределение по длине амплитуд скорости колебаний образца и подложки, а модуль Е упругости определяют из соотношения ((ч (х) .Ъ ° (уt+ p„-t„) — «2v (х)bptgdx
Š— — — — — — ——
У Pt „+2 t2 /t+4/3. t> /t23 ((х) dx где Ъ вЂ” ширина образца; у„, p — плотности исследуемого материала и материала подложки соответственно;
t„ t — - толщина слоя исследуемого материала и подложки соответственно;



www.findpatent.ru
Способ определения модуля упругости материала при помощи виброударного процесса математического маятника, соударяющегося с исследуемым материалом
Изобретение относится к способу определения модуля упругости материала. Технический результат заключается в определении модуля упругости в материале без применения сложных технических устройств, включая электронные блоки измерения частоты колебаний, что удешевляет процедуру определения модуля упругости; более низкая частота рабочего процесса уменьшает влияние рассеяния энергии в исследуемом образце. Способ заключается в определении периода угловых колебаний математического маятника, представляющего собой боек из жесткого материала, подвешенного на нерастяжимой нити, который соударяется со стержнем, выполненным из исследуемого материала, и определении модуля упругости по формуле:
где Т12 - полный период колебаний, g - ускорение свободного падения, l - длина нерастяжимой нити, h - толщина измеряемого образца, F - площадь сечения измеряемого образца, m - масса металлического шарика. 2 ил.
Изобретение относится к способу определения модуля упругости материала на стенде.
Известен способ определения модуля упругости материала, определяемого по ГОСТ-16297-80 «Материалы звукоизоляционные и звукопоглощающие. Методы испытаний», принятый за прототип.
К причинам, препятствующим достижению нижеуказанного результата при использовании известного способа, принятого за прототип, относятся то, что реализация известного способа для определения модуля упругости сопровождается поиском резонансной частоты колебаний на спецстенде. Причем подвижная часть установки, то есть испытуемый образец, по своей массе m соизмерима с массой столика вибратора. Согласно ГОСТ-16297-80 модуль упругости определяют по формуле:
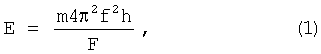
где f - частота резонанса, Гц;
m - масса груза, кг;
h - высота образца под нагрузкой, м;
F - общая площадь одновременно испытываемых образцов, м2.
Величина m является не вполне определенной, так как в нее входит масса столика, что вносит погрешность в результат измерения, и, кроме того, измеряемая частота f ввиду малой длины образца оказывается весьма высокой настолько, что рассеяние энергии при колебаниях может оказывать существенное влияние на величину измеряемого модуля упругости. Установка сама по себе представляет сложное инженерное сооружение.
Технический результат - определение модуля упругости в материале без применения сложных технических устройств, включая электронные блоки измерения частоты колебаний, что удешевляет процедуру определения модуля упругости, более низкую частоту рабочего процесса, что уменьшает влияние рассеяния энергии в исследуемом образце.
Особенности заключаются в простоте измерения периода колебаний, состоящего из двух частей: свободного движения маятника в воздушной среде и части периода, когда маятник взаимодействует с изучаемым образцом. Маятник совершает виброударный процесс, а наблюдатель фиксирует n колебаний маятника, после чего определяется период его колебаний, поделив общее время на число колебаний.
Сущность изобретения заключается в следующем: определяется модуль упругости в материале в результате анализа виброударного процесса математического маятника с препятствием, представляющим из себя упругий стержень, выполненный из исследуемого материала.
Сущность изобретения поясняется чертежами, где на Фиг.1 изображен общий вид стенда, на Фиг.2 представлено пояснение к теоретическому обоснованию.
Математический маятник в виде бойка из жесткого материала подвешивают на нерастяжимой нити, после чего боек отводят на определенный угол и свободно отпускают. Боек соударяется с боковой опорой, которой является стержень из исследуемого материала. Измеряется время и количество соударений, после чего определяется модуль упругости материала, из которого выполнен исследуемый образец.
Способ основан на следующих теоретических соображениях.
На первом этапе дифференциальное уравнение движения маятника имеет вид:

где m - масса маятника, l - длина нерастяжимой нити.
На втором этапе:

где с - жесткость исследуемого образца.
Частота на первом этапе определяется выражением:

Частота на втором этапе будет:

Две амплитуды колебания на первом этапе осуществляются за следующее время:

С учетом (4):
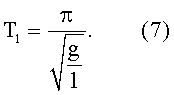
На втором этапе, во время взаимодействия с препятствием, жесткость которого измеряется, период колебаний равен:

Таким образом, период колебаний нелинейного процесса, состоящего из двух частей, будет:

Измеряя период колебаний, например, при помощи секундомера, из формулы (9) находим жесткость образца по формуле:

Данный способ определения жесткости можно применять для определения жесткости тонкостенных элементов конструкции автомобилей, декоративной отделки. Поскольку

то согласно (10) и (11)

Данное изобретение было экспериментально проверено при испытании резины. При этом получено: а) согласно формуле (1) Е=9,431 МПа.
б) согласно формуле (12) Е=8,96 МПа погрешность составила 5%.
Способ определения модуля упругости материала при помощи виброударного процесса математического маятника, соударяющегося с исследуемым материалом, отличающийся тем, что фиксируют последовательность угловых отклонений математического маятника при его соударении с препятствием в виде упругого стержня, выполненного из исследуемого материала, определяют период колебаний, после чего модуль упругости определяют по формуле: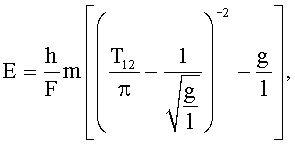 где h - толщина измеряемого образца,F - площадь сечения измеряемого образца,m - масса металлического шарика,Т12 - полный период колебаний,g - ускорение свободного падения,l - длина нерастяжимой нити.
где h - толщина измеряемого образца,F - площадь сечения измеряемого образца,m - масса металлического шарика,Т12 - полный период колебаний,g - ускорение свободного падения,l - длина нерастяжимой нити.
www.findpatent.ru










