УТОЧНЕНИЕ ХАРАКТЕРА ЗАВИСИМОСТИ МОДУЛЯ УПРУГОСТИ ОТ ПРОЧНОСТИ БЕТОНА. Особенности взаимосвязи модуля упругости и прочности бетона
ОСОБЕННОСТИ ВЗАИМОСВЯЗИ МОДУЛЯ УПРУГОСТИ И ПРОЧНОСТИ БЕТОНА
ВЫСОКОПРОЧНЫЙ БЕТОН
Полученное выражение (V.15) дает возможность сформулировать общее положение о характере зависимости меж - ду упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что оца не является однозначной и ее вид определяется, по крайней мере, еще двумя конкретными характеристиками бетона — содержанием цементного теста в смеси и упругими свойствами использованного заполнителя.
Таким образом, в координатной системе Ех — Rx выражение (V.15) описывает некоторую область, границы которой определяются изменчивостью обеих указанных характеристик бетона. Ориентируясь на реальные для тяжелого бетона пределы колебания величин Е3 = (4-f-6)105 и рт = 0,15^-0,30, можно убедиться из рис. 42, что в результате этого модуль упругости бетона Ех при неизменной прочности Rx может изменяться более чем в полтора раза. Если же одновременно рассматривать и песчаные бетоны (растворы), у которых обычно рт > 0,3, то область возможных значений Ех еще более расширяется за счет смещения ее нижней границы. При рт = 1 выражение (V. 15) переходит в зависимость для чистого цементного камня (показана на рисунке пунктиром).
Любая эмпирическая зависимость для модуля упругости бетона в виде (V.4), т. е. в функции только прочности бетона, является одним из частных случаев выражения (V.15) при определенных фиксированных значениях параметров ф = const (т. е. Е3 = const) и рт = const [111]. Это следует из сопоставления формул (V.15) и (V.4), которые связаны соотношениями:
| Јm.10-6 = 5q>; S = 800ф/?т. |
Для тяжелого бетона на крупном заполнителе при изменении £3иртв указанных ранее границах числовые зна-
Рис. 42. Изменчивость корреляционных связей между модулем упругости и прочностью тяжелого бетона по экспериментальным данным (цифры в скобках соответствуют номерам групп серий испытаний по табл. 6)
| £г Ю'5, кГ/см2 КГ/см2 |
/—пределы изменения модуля fy пру ГОСТИ по выражению (V.15) для тяжелых бетонов на крупном заполнителе; 2 —то же, для чистого цементого камня
Чений коэффициентов Ёт и S в формулах типа (V.4) варьируются в весьма широких пределах: Ет = (4,1-7-5,8)105 и s = 100—300. Для песчаных растворов эти значения еще больше. Для цементного камня SK = 800; это предельная величина.
Разнообразные сочетания характеристик £3 и рт, которые могут встретиться на практике, обусловливают поэтому существование бесчисленного множества частных зависимостей Ех = F(Rx), описываемых выражением (V.15). Примером может служить изменчивость корреляционных связей Ех = F(Rx) для бетонов на крупном заполнителе, наблюдаемая в большом числе экспериментов (см. рис. 42). Хотя каждая из корреляционных кривых, соответствующая группе серий испытаний (при Е3 ж const и рТ «
Const), сама по себе достаточно устойчива (см. табл. 6), совокупность этих кривых покрывает фактически обширную область, определяемую на рис. 42 выражением (V.15).
Попытка аппроксимировать такое многообразие связей на рис. 42 в виде некоторой общей зависимости (в функции только прочности бетона) приводит, естественно, к резкому возрастанию разброса опытных величин по отношению к расчетным. В сравнении с большинством частных корреляционных связей среднеквадратичное отклонение в этом случае увеличивается, по крайней мере, в 3—5 раз.
Поэтому нормирование модуля упругости в функции только его прочности обеспечивает сугубо ориентировочную оценку искомой величины. Большинство обычно предлагаемых зависимостей типа (V.4) (см. табл. 5) не выходит за пределы все той же области на рис. 42, а расхождения в числовых значениях коэффициентов Ет и S (см. табл. 5) свидетельствуют лишь о том, что они получены для бетонов, индивидуальные характеристики которых в среднем не были одинаковы. Степень этих различий, установленная на основе соотношений (V.16) и (V.17), отчетливо видна из табл. 7.
Поскольку любая из зависимостей в форме (V.4) справедлива, как это следует из табл. 7, только при наличии определенного заполнителя и при его неизменной дозировке в бетонной смеси ни одну из них нельзя считать универсальной. Не случайно поэтому эмпирические формулы, рекомендуемые специально для песчаных бетонов (см. табл. 7), отражают характерное для них по сравнению с обычными бетонами повышенное содержание цементного теста рт.
| Материал | По данным | Рекомендуемые значения эмпирических коэффициентов в формуле (V.4) | Средние характеристики бетонов, для которых справедлива данная рекомендация | ||
| F | S | | | Рт | ||
| Бетон | Графа [144] . . . Роша [183] . . . СНиП и СН 365- 67...................... | 589 ООО 550 ООО 530 ООО | 176 187 200 | 615 000 565 000 540 000 | 0,186 0,213 0,236 |
| Раствор | Роша [183] . . . СНиП.................................. | 600 000 400 000 | 375 200 | 690 000 365 000 | 0,390 0,313 |
Данные табл. 7 позволяют не только объяснить существо расхождений между различными предложениями, но и сразу судить об их характерных особенностях и недостатках. Выясняется, например, что часто используемая формула Графа, в принципе вообще неприменима для современных тяжелых (тем более высокопрочных) бетонов, которые отличаются существенно более высокими средними значениями рт (см. табл. 7, данные СНиП и СН 365-67). Рекомендации СНиП для песчаных растворов неправильно интерпретируют их главное отличие от бетонов, дифференцируя лишь значения коэффициента Ет. В результате данные СНиП отражают искусственно заниженные величины модуля упругости заполнителя (Е3 = 3,65 • 105), хотя фактически у кварцевого песка он в среднем не ниже, чем у гранита (см. предложение Роша).
Влияние обоих рассмотренных факторов наряду с прочностью на величину модуля упругости бетона само по себе не является неожиданным. Оно обнаруживалось в разное время в ряде экспериментов [98, 119, 129, 143, 160, 164]. Однако полученное выражение (V.15) впервые дает возможность разделить это влияние в количественном отношении и оценить его независимо одно от другого.
Все три характеристики бетона (RXf Е3 и рТ) слабо связаны друг с другом и могут встречаться практически в произвольных сочетаниях. Поэтому выражение (V.15) позволяет описать некоторые закономерности, которые никак не отражаются в существующих методах оценки величины модуля упругости бетона. Сказанное подтверждается результатами ряда экспериментов [119, 138, 165, 185 и др.].
Опыты Рюша, Кордины и Гильсдорфа [165] —тот редкий случай, когда модуль упругости заполнителя варьировался в широких пределах и непосредственно измерялась его величина (табл. 8). Две другие исходные характеристики — кубиковая прочность бетона и содержание цементного теста в смеси — сохранялись практически неизменными. Возраст бетона при испытании составлял 28 суток. В табл. 8 сопоставлены результаты прямых измерений модуля упругости бетонов на разных заполнит елях и расчета этих величин по формуле (V.15).
| Таблица 8
|
Из табл. 8 видно, что хотя расчетные значения во всех случаях несколько выше опытных, они полностью отражают экспериментальную закономерность, которая обнаруживается при практически возможном изменении упругих свойств заполнителя. И опытные и расчетные значения модуля упругости бетона могут отличаться за счет только этого фактора почти в 4 раза. Данные СНиП, приведенные для сравнения, отражают в тех же условиях лишь незначительное влияние колебаний прочности бетона на модуль упругости.
Другой пример, заимствованный из опытов Боломея [119], когда при неизменной прочности бетона и использовании одинакового заполнителя в широких пределах варьировалось содержание цементного теста в бетонных смесях, приведен в табл. 9. Возраст бетона при испытании составлял 90 суток.
Можно убедиться, что выражение (V.15) и в этом случае хорошо отражает экспериментальные закономерности, сво-
| Модуль упругости заполнителя | Кубиковая прочность бетона | Содержание цементного теста | Значения модуля упругости бетона Ех - 10 | ||
| Ез-10-5 (ориентировочно) | Измеренные | Расчетные | По СНиП | ||
| 6,1 | 306 302 297 307 325 | 0,136 0,159 0,171 0,258 0,378 | 4,05 3,92 4,01 3,22 2,7 | 4,15 3,92 3,81 3,25 2,74 | 3,2 3,19 3,16 3,21 3,28 |
Дящиеся к изменению модуля упругости бетона почти в 1,5 раза при неизменной его прочности за счет только влияния содержания цементного теста. Как и ранее, рекомендации СНиП не учитывают возможность столь существенных изменений.
На практике обычно одновременно изменяются не одна, а сразу две (чаще всего Rx и рт) или даже все три характеристики бетона, определяющие величину его модуля упругости. Это может привести к полному нарушению общепринятых закономерностей связи между модулем упругости и прочностью бетона (см. рис. 35). Указанные явления, необъяснимые с точки зрения существующих подходов к оценке упругих свойств бетона, находятся, однако, в полном соответствии с характером выражения (V. 15). В табл. 10 сравниваются средние величины модулей упругости, полученные в упомянутых опытах, и его расчетные значения, вычисленные по формуле (V. 15).
Как видно из табл. 10, выражение (V. 15) во всех случаях правильно описывает достаточно сложные закономерности изменения модуля упругости бетона, наблюдаемые в рассматриваемых экспериментах и состоящие в заметном (до 20—27%) падении величины модуля при повышении прочности сверх некоторого предела.
На основе выражения (V. 15) это явление легко объяснимо и представляется вполне закономерным. Увеличение прочности бетона достигалось в опытах при одновременном росте содержания цементного теста в смесях. Поскольку такое изменение обоих факторов прямо противоположно отражается на величине модуля упругости бетона, характер получаемых связей с прочностью может быть самым разнообразным. Как правило, начиная с некоторого значения
| Автор экспериментальных | О CQ | Модуль упругости заполнителя (ориентировочно) | Кубиковая прочность бетона | Содержание цементного теста рт | Значения модуля упругости бетона £т.10-5 | С К | ||
| Данных | G er « СО 5 Л 5 л 3 ю X о | Ят | Измеренные | Расчетные | Д и О С | |||
| Уокер [202] | 5 5 5 5 5 5 5 | 4,9 | 171 229 276 326 372 425 550 | 0,149 0,191 0,22 0,264 0,34 0,494 0,74 | 3,07 2,76 3.1 3.2 2,89 2,71 2,26 | 2,91 2,96 3,02 3 2,87 2,58 2,4 | 2,44 2,73 3,07 3,28 3,44 3,6 3,88 | |
| Ричарт, Брандцаег и Браун [185] | 3 3 3 3 3 3 | 3,1 | 63 114 154 249 288 . 341 | 0,181 0,211 0,248 0,317 0,387 0,545 | 1,04 1,39 1,78 2,16 1,9 1,99 | 1,32 1,68 1,82 2,05 2,03 1,96 | 1.93 2,3 2.94 2,36* 3,52* | |
| Фройденталь и Ролл [138] | 8 2 8 8 | 5,8 | ( 386 493 479 і 696 | 0,203 0,272 0,367 0,565 | 3,94 3,66 3,25 3,16 | 3,81 3,72 3,28 3,14 | 3,48 3,78 3,74 (4,11)** |
| * Значения приняты для песчаных растворов. ** Получено экстраполяцией. |
Прочности, дальнейшее ее повышение не может компенсировать влияния растущего содержания цементного теста. Поэтому модуль упругости, достигнув максимальной величины, начинает снижаться. Получаемая закономерность прямо противоположна той, которая предусматривается в этих случаях рекомендациями нормативных документов.
Таким образом, выражение (V. 15), являясь в значительной мере универсальным, отвечает одновременно и теоретическим представлениям, и результатам большого числа экспериментов. С этой точки зрения оно имеет бесспорные преимущества перед существующими эмпирическими формулами для расчета модуля упругости бетона и может быть использовано для практической оценки ожидаемых величин модуля упругости обычного бетона, цемент - но-песчаного раствора и даже чистого цементного камня
Ёйе зависимости of прочностных характеристик этих материалов (во всяком случае до прочностей порядка 1000 кГ/см2). Выражение (V.15) позволяет также учесть некоторые специфические закономерности изменения модуля упругости бетона (раствора) в самых различных условиях. Все это открывает реальные пути повышения надежности прогнозов упругих характеристик бетона при проектировании конструкций.
Кольца колодцев были и остаются очень востребованным строительным материалом. К слову, кольца колодцев приобретают не только те, чья деятельность связана с водоснабжением и канализацией, но и телефонисты, Интернет-провайдеры и, конечно …
Об усадке тяжелого бетона имеется не меньше экспериментальных данных, чем о его ползучести. Попытки- использовать эти данные для получения общих количественных закономерностей явления содержатся в ряде работ. При оценке возможной …
msd.com.ua
Особенности взаимосвязи модуля упругости и прочности бетона
Полученное выражение (V. 15) дает возможность сформулировать общее положение о характере зависимости между упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что она не является однозначной и ее вид определяется, по крайней мере, еще двумя конкретными характеристиками бетона — содержанием цементного теста в смеси и упругими свойствами использованного заполнителя. Таким образом, в координатной системе Ех — Rx выражение описывает некоторую область, границы которой определяются изменчивостью обеих указанных характеристик бетона. Ориентируясь на реальные для тяжелого бетона пределы колебания величин Е3 = (4-f-6)105 и рт = 0,15^-0,30, можно убедиться из рис. 42, что в результате этого модуль упругости бетона Ех при неизменной прочности Rx может изменяться более чем в полтора раза. Если же одновременно рассматривать и песчаные бетоны (растворы), у которых обычно /?т > 0,3, то область возможных значений Ех еще более расширяется за счет смещения ее нижней границы. При рт = 1 выражение (V. 15) переходит в зависимость для чистого цементного камня (показана на рисунке пунктиром). Любая эмпирическая зависимость для модуля упругости бетона в виде (V.4), т. е. в функции только прочности бетона, является одним из частных случаев выражения при определенных фиксированных значениях параметров ф = const (т. е. Е3 — const) ирт = const. Для тяжелого бетона на крупном заполнителе при изменении Е3 и рт в указанных ранее границах числовые значения коэффициентов Ёт и s в формулах типа (V.4) варьируются в весьма широких пределах: Ет = (4,1^-5,8)105 и s = 100^-300. Для песчаных растворов эти значения еще больше. Для цементного камня 5К = 800; это предельная величина. Разнообразные сочетания характеристик Е3 и рТ, которые могут встретиться на практике, обусловливают поэтому существование бесчисленного множества частных зависимостей Ех = f(Rx), описываемых выражением (V. 15). Примером может служить изменчивость корреляционных связей Ех = f{Rx) Для бетонов на крупном заполнителе, наблюдаемая в большом числе экспериментов (см. рис. 42). Хотя каждая из корреляционных кривых, соответствующая группе серий испытаний (), сама по себе достаточно устойчива (см. табл. 6), совокупность этих кривых покрывает фактически обширную область, определяемую на рис. 42 выражением (V. 15). Попытка аппроксимировать такое многообразие связей на рис. 42 в виде некоторой общей зависимости (в функции только прочности бетона) приводит, естественно, к резкому возрастанию разброса опытных величин по отношению к расчетным. В сравнении с большинством частных корреляционных связей среднеквадратичное отклонение в этом случае увеличивается, по крайней мере, в 3—5 раз. Поэтому нормирование модуля упругости в функции только его прочности обеспечивает сугубо ориентировочную оценку искомой величины. Большинство обычно предлагаемых зависимостей типа (V.4) (см. табл. 5) не выходит за пределы все той же области на рис. 42, а расхождения в числовых значениях коэффициентов Ет и s (см. табл. 5) свидетельствуют лишь о том, что они получены для бетонов, индивидуальные характеристики которых в среднем не были одинаковы. Степень этих различий, установленная на основе соотношений (V. 16) и (V. 17), отчетливо видна из табл. 7. Поскольку любая из зависимостей в форме (V.4) справедлива, как это следует из табл. 7, только при наличии определенного заполнителя и при его неизменной дозировке в бетонной смеси ни одну из них нельзя считать универсальной. Не случайно поэтому эмпирические формулы, рекомендуемые специально для песчаных бетонов (см. табл. 7), отражают характерное для них по сравнению с обычными бетонами повышенное содержание цементного теста рТ. Данные табл. 7 позволяют не только объяснить существо расхождений между различными предложениями, но и сразу судить об их характерных особенностях и недостатках. Выясняется, например, что часто используемая формула Графа, в принципе вообще неприменима для современных тяжелых (тем более высокопрочных) бетонов, которые отличаются существенно более высокими средними значениями рт (см. табл. 7, данные СНиП и СН 365-67). Рекомендации СНиП для песчаных растворов неправильно интерпретируют их главное отличие от бетонов, дифференцируя лишь значения коэффициента Ет. В результате данные СНиП отражают искусственно заниженные величины модуля упругости заполнителя (Es ==3,65 • 105), хотя фактически у кварцевого песка он в среднем не ниже, чем у гранита (см. предложение Роша). Влияние обоих рассмотренных факторов наряду с прочностью на величину модуля упругости бетона само по себе не является неожиданным. Оно обнаруживалось в разное время в ряде экспериментов [98, 119, 129, 143, 160, 164]. Однако полученное выражение (V. 15) впервые дает возможность разделить это влияние в количественном отношении и оценить его независимо одно от другого. Все три характеристики бетона (RX1 E3 и рт) слабо связаны друг с другом и могут встречаться практически в произвольных сочетаниях. Поэтому выражение позволяет описать некоторые закономерности, которые никак не отражаются в существующих методах оценки величины модуля упругости бетона. Сказанное подтверждается результатами ряда экспериментов [119, 138, 165, 185 и др.З. Опыты Рюша, Кордины и Гильсдорфа —тот редкий случай, когда модуль упругости заполнителя варьировался в широких пределах и непосредственно измерялась его величина (табл. 8). Две другие исходные характеристики — кубиковая прочность бетона и содержание цементного теста в смеси — сохранялись практически неизменными. Возраст бетона при испытании составлял 28 суток. В табл. 8 сопоставлены результаты прямых измерений модуля упругости бетонов на разных заполнителях и расчета этих величин по формуле. Из табл. 8 видно, что хотя расчетные значения во всех случаях несколько выше опытных, они полностью отражают экспериментальную закономерность, которая обнаруживается при практически возможном изменении упругих свойств заполнителя. И опытные и расчетные значения модуля упругости бетона могут отличаться за счет только этого фактора почти в 4 раза. Данные СНиП, приведенные для сравнения, отражают в тех же условиях лишь незначительное влияние колебаний прочности бетона на модуль упругости. Другой пример, заимствованный из опытов Боломея, когда при неизменной прочности бетона и использовании одинакового заполнителя в широких пределах варьировалось содержание цементного теста в бетонных смесях, приведен в табл. 9. Возраст бетона при испытании составлял 90 суток. Можно убедиться, что выражение и в этом случае хорошо отражает экспериментальные закономерности, сводящиеся к изменению модуля упругости бетона почти в 1,5 раза при неизменной его прочности за счет только влияния содержания цементного теста. Как и ранее, рекомендации СНиП не учитывают возможность столь существенных изменений. На практике обычно одновременно изменяются не одна, а сразу две (чаще всего ^т и рт) или даже все три характеристики бетона, определяющие величину его модуля упругости. Это может привести к полному нарушению общепринятых закономерностей связи между модулем упругости и прочностью бетона (см. рис. 35). Указанные явления, необъяснимые с точки зрения существующих подходов к оценке упругих свойств бетона, находятся, однако, в полном соответствии с характером выражения. В табл. 10 сравниваются средние величины модулей упругости, полученные в упомянутых опытах, и его расчетные значения, вычисленные по формуле . Как видно из табл. 10, выражение во всех случаях правильно описывает достаточно сложные закономерности изменения модуля упругости бетона, наблюдаемые в рассматриваемых экспериментах и состоящие в заметном (до 20—27%) падении величины модуля при повышении прочности сверх некоторого предела. На основе выражения это явление легко объяснимо и представляется вполне закономерным. Увеличение прочности бетона достигалось в опытах при одновременном росте содержания цементного теста в смесях. Поскольку такое изменение обоих факторов прямо противоположно отражается на величине модуля упругости бетона, характер получаемых связей с прочностью может быть самым разнообразным. Как правило, начиная с некоторого значения прочности, дальнейшее ее повышение не может компенсировать влияния растущего содержания цементного теста. Поэтому модуль упругости, достигнув максимальной величины, начинает снижаться. Получаемая закономерность прямо противоположна той, которая предусматривается в этих случаях рекомендациями нормативных документов. Таким образом, выражение (V. 15), являясь в значительной мере универсальным, отвечает одновременно и теоретическим представлениям, и результатам большого числа экспериментов. С этой точки зрения оно имеет бесспорные преимущества перед существующими эмпирическими формулами для расчета модуля упругости бетона и может быть использовано для практической оценки ожидаемых величин модуля упругости обычного бетона, цемент-но-песчаного раствора и даже чистого цементного камня вне зависимости от прочностных характеристик этих материалов (во всяком случае до прочностей порядка 1000 кГ/см2). Выражение позволяет также учесть некоторые специфические закономерности изменения модуля упругости бетона (раствора) в самых различных условиях. Все это открывает реальные пути повышения надежности прогнозов упругих характеристик бетона при проектировании конструкций.vogean.com
Особенности взаимосвязи модуля упругости и прочности бетона
Полученное выражение (V. 15) дает возможность сформулировать общее положение о характере зависимости между упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что она не является однозначной и ее вид определяется, по крайней мере, еще двумя конкретными характеристиками бетона — содержанием цементного теста в смеси и упругими свойствами использованного заполнителя. Таким образом, в координатной системе Ех — Rx выражение описывает некоторую область, границы которой определяются изменчивостью обеих указанных характеристик бетона. Ориентируясь на реальные для тяжелого бетона пределы колебания величин Е3 = (4-f-6)105 и рт = 0,15^-0,30, можно убедиться из рис. 42, что в результате этого модуль упругости бетона Ех при неизменной прочности Rx может изменяться более чем в полтора раза. Если же одновременно рассматривать и песчаные бетоны (растворы), у которых обычно /?т > 0,3, то область возможных значений Ех еще более расширяется за счет смещения ее нижней границы. При рт = 1 выражение (V. 15) переходит в зависимость для чистого цементного камня (показана на рисунке пунктиром). Любая эмпирическая зависимость для модуля упругости бетона в виде (V.4), т. е. в функции только прочности бетона, является одним из частных случаев выражения при определенных фиксированных значениях параметров ф = const (т. е. Е3 — const) ирт = const. Для тяжелого бетона на крупном заполнителе при изменении Е3 и рт в указанных ранее границах числовые значения коэффициентов Ёт и s в формулах типа (V.4) варьируются в весьма широких пределах: Ет = (4,1^-5,8)105 и s = 100^-300. Для песчаных растворов эти значения еще больше. Для цементного камня 5К = 800; это предельная величина. Разнообразные сочетания характеристик Е3 и рТ, которые могут встретиться на практике, обусловливают поэтому существование бесчисленного множества частных зависимостей Ех = f(Rx), описываемых выражением (V. 15). Примером может служить изменчивость корреляционных связей Ех = f{Rx) Для бетонов на крупном заполнителе, наблюдаемая в большом числе экспериментов (см. рис. 42). Хотя каждая из корреляционных кривых, соответствующая группе серий испытаний (), сама по себе достаточно устойчива (см. табл. 6), совокупность этих кривых покрывает фактически обширную область, определяемую на рис. 42 выражением (V. 15). Попытка аппроксимировать такое многообразие связей на рис. 42 в виде некоторой общей зависимости (в функции только прочности бетона) приводит, естественно, к резкому возрастанию разброса опытных величин по отношению к расчетным. В сравнении с большинством частных корреляционных связей среднеквадратичное отклонение в этом случае увеличивается, по крайней мере, в 3—5 раз. Поэтому нормирование модуля упругости в функции только его прочности обеспечивает сугубо ориентировочную оценку искомой величины. Большинство обычно предлагаемых зависимостей типа (V.4) (см. табл. 5) не выходит за пределы все той же области на рис. 42, а расхождения в числовых значениях коэффициентов Ет и s (см. табл. 5) свидетельствуют лишь о том, что они получены для бетонов, индивидуальные характеристики которых в среднем не были одинаковы. Степень этих различий, установленная на основе соотношений (V. 16) и (V. 17), отчетливо видна из табл. 7. Поскольку любая из зависимостей в форме (V.4) справедлива, как это следует из табл. 7, только при наличии определенного заполнителя и при его неизменной дозировке в бетонной смеси ни одну из них нельзя считать универсальной. Не случайно поэтому эмпирические формулы, рекомендуемые специально для песчаных бетонов (см. табл. 7), отражают характерное для них по сравнению с обычными бетонами повышенное содержание цементного теста рТ. Данные табл. 7 позволяют не только объяснить существо расхождений между различными предложениями, но и сразу судить об их характерных особенностях и недостатках. Выясняется, например, что часто используемая формула Графа, в принципе вообще неприменима для современных тяжелых (тем более высокопрочных) бетонов, которые отличаются существенно более высокими средними значениями рт (см. табл. 7, данные СНиП и СН 365-67). Рекомендации СНиП для песчаных растворов неправильно интерпретируют их главное отличие от бетонов, дифференцируя лишь значения коэффициента Ет. В результате данные СНиП отражают искусственно заниженные величины модуля упругости заполнителя (Es ==3,65 • 105), хотя фактически у кварцевого песка он в среднем не ниже, чем у гранита (см. предложение Роша). Влияние обоих рассмотренных факторов наряду с прочностью на величину модуля упругости бетона само по себе не является неожиданным. Оно обнаруживалось в разное время в ряде экспериментов [98, 119, 129, 143, 160, 164]. Однако полученное выражение (V. 15) впервые дает возможность разделить это влияние в количественном отношении и оценить его независимо одно от другого. Все три характеристики бетона (RX1 E3 и рт) слабо связаны друг с другом и могут встречаться практически в произвольных сочетаниях. Поэтому выражение позволяет описать некоторые закономерности, которые никак не отражаются в существующих методах оценки величины модуля упругости бетона. Сказанное подтверждается результатами ряда экспериментов [119, 138, 165, 185 и др.З. Опыты Рюша, Кордины и Гильсдорфа —тот редкий случай, когда модуль упругости заполнителя варьировался в широких пределах и непосредственно измерялась его величина (табл. 8). Две другие исходные характеристики — кубиковая прочность бетона и содержание цементного теста в смеси — сохранялись практически неизменными. Возраст бетона при испытании составлял 28 суток. В табл. 8 сопоставлены результаты прямых измерений модуля упругости бетонов на разных заполнителях и расчета этих величин по формуле. Из табл. 8 видно, что хотя расчетные значения во всех случаях несколько выше опытных, они полностью отражают экспериментальную закономерность, которая обнаруживается при практически возможном изменении упругих свойств заполнителя. И опытные и расчетные значения модуля упругости бетона могут отличаться за счет только этого фактора почти в 4 раза. Данные СНиП, приведенные для сравнения, отражают в тех же условиях лишь незначительное влияние колебаний прочности бетона на модуль упругости. Другой пример, заимствованный из опытов Боломея, когда при неизменной прочности бетона и использовании одинакового заполнителя в широких пределах варьировалось содержание цементного теста в бетонных смесях, приведен в табл. 9. Возраст бетона при испытании составлял 90 суток. Можно убедиться, что выражение и в этом случае хорошо отражает экспериментальные закономерности, сводящиеся к изменению модуля упругости бетона почти в 1,5 раза при неизменной его прочности за счет только влияния содержания цементного теста. Как и ранее, рекомендации СНиП не учитывают возможность столь существенных изменений. На практике обычно одновременно изменяются не одна, а сразу две (чаще всего ^т и рт) или даже все три характеристики бетона, определяющие величину его модуля упругости. Это может привести к полному нарушению общепринятых закономерностей связи между модулем упругости и прочностью бетона (см. рис. 35). Указанные явления, необъяснимые с точки зрения существующих подходов к оценке упругих свойств бетона, находятся, однако, в полном соответствии с характером выражения. В табл. 10 сравниваются средние величины модулей упругости, полученные в упомянутых опытах, и его расчетные значения, вычисленные по формуле . Как видно из табл. 10, выражение во всех случаях правильно описывает достаточно сложные закономерности изменения модуля упругости бетона, наблюдаемые в рассматриваемых экспериментах и состоящие в заметном (до 20—27%) падении величины модуля при повышении прочности сверх некоторого предела. На основе выражения это явление легко объяснимо и представляется вполне закономерным. Увеличение прочности бетона достигалось в опытах при одновременном росте содержания цементного теста в смесях. Поскольку такое изменение обоих факторов прямо противоположно отражается на величине модуля упругости бетона, характер получаемых связей с прочностью может быть самым разнообразным. Как правило, начиная с некоторого значения прочности, дальнейшее ее повышение не может компенсировать влияния растущего содержания цементного теста. Поэтому модуль упругости, достигнув максимальной величины, начинает снижаться. Получаемая закономерность прямо противоположна той, которая предусматривается в этих случаях рекомендациями нормативных документов. Таким образом, выражение (V. 15), являясь в значительной мере универсальным, отвечает одновременно и теоретическим представлениям, и результатам большого числа экспериментов. С этой точки зрения оно имеет бесспорные преимущества перед существующими эмпирическими формулами для расчета модуля упругости бетона и может быть использовано для практической оценки ожидаемых величин модуля упругости обычного бетона, цемент-но-песчаного раствора и даже чистого цементного камня вне зависимости от прочностных характеристик этих материалов (во всяком случае до прочностей порядка 1000 кГ/см2). Выражение позволяет также учесть некоторые специфические закономерности изменения модуля упругости бетона (раствора) в самых различных условиях. Все это открывает реальные пути повышения надежности прогнозов упругих характеристик бетона при проектировании конструкций.www.vogean.com
УТОЧНЕНИЕ ХАРАКТЕРА ЗАВИСИМОСТИ МОДУЛЯ УПРУГОСТИ ОТ ПРОЧНОСТИ БЕТОНА
ВЫСОКОПРОЧНЫЙ БЕТОН
У бетонов, изготовленных на плотном прочном заполнителе, характеристика цементного камня играет важную роль в формировании связей прочности и деформативности этого материала.
Современные данные о влиянии структуры цементного камня на его физико-механические свойства ( см. главу II) не позволяют получить надежных критериев для необходимых количественных оценок этих свойств. Однако удается проследить некоторые качественные зависимости.
Величина пористости цементного камня ип, от которой в соответствии с выражениями (V.2) или (V.3) зависит преимущественно модуль упругости цементного камня Ек, определяется В/Ц пасты и степенью гидратации цемента а.
Значение пористости может быть оценено по эмпирическому выражению [187]:
| Рис. 36. Принципиальный характер зависимостей модуля упругости Ек и прочности RK Цементного камня от Z = Ц/В |
0,47а В/Ц + 0,32 1 —0,47а
(V.6)
В/Ц + 0,32
Цементно-водное отношение насты.
При заданной степени гидратации (например, а = 0,5) изменение модуля упругости по формуле (V.3) с учетом (V.6) показано на рис. 36 (кривая Ек).
Прочность цементного камня обнаруживает несколько иную закономерность связи с цементно-водным отношением 2. В обычном диапазоне изменения г и при определенной степени гидратации эта связь [187, 210] практически прямолинейна (прямая RK).
Условно экстраполируя зависимости для Ек и RK на рис. 36, можно исходить из того, что при возрастании прочности RK модуль упругости камня Ек стремится к некоторому пределу Ект. Поэтому связь между этими величинами может быть описана функцией вида:
І R*
SK + ^K
Аналогичной той, которая используется для расчета модуля упругости бетона по формулам типа (V.4).
Справедливость этого положения была проверена нами с использованием опытных значений прочности и модуля упругости чистого цементного, камня [79, 88, 166, 187, 202]. При обработке этих данных применяли несложный прием, позволяющий оценить одновременно величины обоих эмпирических параметров, входящих в выражение (V.7). Для этого отыскивалась корреляционная связь для всей совокупности опытных точек, нанесенных в координатах У = RJEK и X = RK. Коэффициенты а0 и Ь0 соответствующего линейного корреляционного уравнения Y — = а0 + Ь0Х имеют вид
Sk А 1
Ект ^кг
Существование тесной корреляционной связи между модулем упругости и прочностью цементного камня (коэффициент корреляции = 0,91) подтверждается рис. 37.
В соответствии с корреляционным уравнением в выражении (V.7) можно принять:
5-10» и 5К = а0 Ект = 160 • 5 = 800.
Ьо
Из сравнения значений Ект и SK с аналогичными эмпирическими константами для бетона видно, что величина Ект получилась примерно того же порядка, как и Ет, а параметр SK, по крайней мере, в 3—4 раза превышает обычно рекомендуемые значения постоянной S (см. табд. 5).
Рассмотренные опытные результаты получены при испытании портландцемента различных видов (всего 13 партий цемента разного минералогического состава и активности, включая отечественный ОБТЦ). Судя по рис. 37, изменение этих характеристик цемента не оказывает заметного влияния на зависимость модуля упругости цементного камня от его прочности. То же самое можно сказатьи о воздействии степени Гидратации цемента, поскольку возраст цементного камня при испытаниях колебался в широких пределах от 1 до 365 суток.
Для того чтобы применить зависимость (V.7) к оценке упругих свойств бетона, следует рассматривать его как двухфазную систему, состоящую из цементного камня с модулем упругости £к и заполнителя с модулем упругости Е3.
С этой целью преобразуем выражение (V. 1) таким образом, чтобы оперировать величинами удельных упругих деформаций бетона (на единицу действующих напряжений) 1/£б, т. е.
(2 — vT) + vT ЕЗ Ек
Еб vT + (2 — vT)E3/EK
Где VT = VK—относительный объем цементного теста (камня) в бетоне.
Выражение (V.8) представлено на рис. 38 в виде серии кривых EJE6 = /i(fT)> каждая из которых соответствуетопределенному значению Е3/Ек (сплошные линии). Для бетонов на заполнителях из прочных пород в подавляющем большинстве случаев EJEK > 1.
Из чисто практических соображений удобнее рассматривать не объемное VT, а весовое содержание цементного теста в бетоне рт, имея в виду используемый обычно способ дозировки составляющих для бетона. Тогда, основываясь на известных соотношениях между величинами VT и рт, удается в значительной мере упростить выражение (V.8). Кривые EJEQ= Fi(VТ), будучи перестроены в виде Ек/Еб = — fт)> дают зависимости, весьма близкие к прямолинейным (пунктирные линии на рис. 38). Это обстоятельство позволяет записать:
Выражение (V.9) достаточно близко к теоретической зависимости (V.8), но им более удобно пользоваться при дальнейших преобразованиях.
Граничные условия в обоих выражениях сохраняются без изменений:
При vT=pT= О £б = £3;
При i>T = pT= 1 Еб = Ек.
Преобразуя выражение (V.9), получим:
1 -1~Рт+—рт. (V.10)
Е 5 EQ Ен
Примем теперь во внимание, что изменение прочности цементного камня и бетона определяется преимущественно одними и теми же факторами (качество цементного клея и степень гидратации цемента). Не уточняя соотношения прочностных показателей чистого цементного камня и соответствующего бетона, можно использовать для предварительных оценок полученную ранее зависимость (V.7), подставив ее в (V.10) в виде:
Скт ^к скт Аб /
Где S в общем случае отличается от
После преобразований имеем:
1 — Рт | SpT | рт __ Е6 Е3 ькт
__ EKm R6 (1 — рТ) + SpT Е3 + R6 Е3 рт
Введя обозначение п = EJEKm, получим окончательно: ^ . (V. 12)
5ртЛ + [1+рт(П-1)]Яб
Параметры £кт и SK, относящиеся к цементному камню, можно рассматривать как некоторые постоянные, не зависящие в определенных пределах от характеристик цемента и степени его гидратации, т. е. возраста (см. стр. 85). Эти же параметры или так или иначе с ними связанные sun присутствуют в формуле (V.12). Поэтому модуль упругости бетона заданной прочности и изготовленного на одном и том же заполнителе не должен зависеть ни от возраста в момент приложения нагрузки, ни от свойств примененного портландцемента. Этот вывод действительно подтверждается опытами Сантареллы [190], Кли - гера [164], Гэриха [151] и Краля [166]. Следовательно, выражение (V.12) справедливо для произвольного возраста т в момент приложения нагрузки и может быть записано в виде:
ФЕкт
Ех = * * , (V.13)
<PSPT + #t
Где ф = 7—.-------------------- тт — безразмерный коэффициент;
1 ~Г Рт П — Ч
Rx — прочность бетона (например, кубиковая) в момент приложения нагрузки.
Выражение (V.13), полученное Е. Н. Щербаковым [111], представляет собой зависимость Ех — F(Rx) в наиболее общей форме. Из (V. 13) непосредственно следует, что при рт = 0 Ех = ЕЗ, а при рт = 1 и S = SK она переходит в выражение (V.7) для расчета модуля упругости цементного камня. Таким образом, эта зависимость одинаково справедлива во всем диапазоне рт и при любой упругой характеристике заполнителя, определяющей величину отношения п = EJEKm.
Выражение (V.13) содержит два параметра s и ф, значения которых нуждаются в экспериментальной проверке,
При этом, если первый из них может рассматриваться в качестве некоторой постоянной, то второй представляет собой функцию преимущественно упругой характеристики заполнителя £3, поскольку содержание цементного теста рт, входящее в выражение для ф, в практически возможных для бетонов случаях оказывает второстепенное влияние на величину этого параметра.
Кольца колодцев были и остаются очень востребованным строительным материалом. К слову, кольца колодцев приобретают не только те, чья деятельность связана с водоснабжением и канализацией, но и телефонисты, Интернет-провайдеры и, конечно …
Полученное выражение (V.15) дает возможность сформулировать общее положение о характере зависимости меж - ду упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что оца не является …
Об усадке тяжелого бетона имеется не меньше экспериментальных данных, чем о его ползучести. Попытки- использовать эти данные для получения общих количественных закономерностей явления содержатся в ряде работ. При оценке возможной …
msd.com.ua
8.5.3. Модуль упругости и деформации бетона при
КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ
Деформации бетона при приложении нагрузки зависят от его состава, свойств составляющих материалов и вида напряженного состояния. Диаграмма сжатия бетона имеет криволинейное очертание, причем кривизна увеличивается с ростом напряжений (рис. 6.4).
С увеличением прочности бетона уменьшается его деформация и кривизна диаграммы . Низкопрочные бетоны имеют даже нисходящую ветвь диаграммы сжатия. Однако на этом участке сплошность материала уже нарушена, в нем возникают микроскопические трещины, отслоение отдельных частей. В железобетонных конструкциях арматура связывает отдельные части бетона в единое целое и для частных случаев расчета конструкций необходимо учитывать нисходящую ветвь диаграммы сжатия бетона.
На характер нарастания деформаций под действием нагрузки влияют также скорость ее приложения, размеры образца, температурно-влажностное состояние бетона и окружающей среды и другие факторы. Деформация бетона включает упругую, пластическуюи псевдопластическуючасти (рис. 6.4):
Соотношение между ними зависит от состава бетона, использованных материалов и других факторов. Величина пластической и псевдопластической частей возрастает с увеличением длительности нагрузки, понижением прочности бетона, увеличением водоцементного отношения, при применении слабых заполнителей.
О деформативных свойствах бетона при приложении нагрузки судят по его модулю деформации, т. е. по отношению напряжения к относительной реформации, вызываемой его действием. Чем выше модуль деформации, тем менее деформативен материал. Поскольку диаграмма сжатия бетона криволинейна, то его модуль деформации зависит от значений относительных напряжений, постепенно понижаясь с их увеличением (рис.6.5), причем тем больше, чем ниже марка бетона. Обычно определяют либо начальный модуль деформации бетона Ео, когда преобладают упругие деформации, либо модуль деформации при определенном значении, например при= 0,5.
На практике используют эмпирические зависимости модуля деформации от различных факторов. Для расчета железобетонных конструкций важна зависимость модуля деформации при можно определить по формуле:
,
где R– прочность бетона.
В действительности модуль деформации может заметно отличаться от средних значений. В табл. 6.2 приведены значения модуля деформации при сжатии некоторых видов бетона, показывающие большое влияние на него технологических факторов.
Важное значение для расчета конструкций и оценки их поведения под нагрузкой имеют величины предельных деформаций, при которых начинается разрушение бетона, По опытным данным, предельная сжимаемость бетона изменяется в пределах 0.0015…0,003, увеличиваясь при повышении прочности бетона.
Предельную сжимаемость бетона можно также увеличивать, применяя более Деформативные компоненты и обеспечивая достаточно надежное сцепление между ними.
Предельная растяжимость бетона составляет 0,0001…0,0015, т.е. примерно в 15…20 раз меньше его предельной сжимаемости.
Предельная растяжимость повышается при введении в бетон пластифицирующих добавок, использовании белитовых цементов, уменьшении крупности заполнителей или при применении заполнителей с высокими деформативными свойствами и сцеплением с цементным камнем.
studfiles.net
АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ЗАКОНОМЕРНОСТЕЙ СВЯЗИ МЕЖДУ МОДУЛЕМ УПРУГОСТИ И ПРОЧНОСТЬЮ ТЯЖЕЛОГО БЕТОНА
ВЫСОКОПРОЧНЫЙ БЕТОН
Справедливость полученного выражения (V.13) была проверена методом, описанным на стр. 84 применительно к цементному камню. В соответствии с этим методом выражение (V.13) представлено в виде:
~~=a0+b0Ru (V.14)
Ех
Где
S
Рт и bQ
Ект ф^кт
Далее отыскивали корреляционные связи для совокупностей опытных точек, нанесенных в координатах Y = = Rx/Ex и X = Rx. Получаемые при этом простые линейные уравнения регрессии позволяют, во-первых, легко судить о наличии и устойчивости корреляционной связи типа (V.13), а во-вторых, оценивать независимо друг от друга одновременно оба искомых параметра S и ср в выражении (V.13). Поскольку Ект = 5 • 105 рассматривается как константа, эти параметры определяются непосредственно коэффициентами корреляционного уравнения вида (V. 14).
Обработке по этой методике с помощью ЭЦВМ была подвергнута большая выборка экспериментальных результатов, полученных разными авторами, начиная с 1920 г. Однако далеко не все имеющиеся опытные данные могли быть использованы. Как видно из выражения (V.14), искомая корреляционная зависимость справедлива только для бетонов, изготовленных на смесях с примерно одинаковым расходом цементного теста и на близких по своим упругим свойствам заполнителях (из условия рт = const и ср = const). Кроме того, для получения надежной корреляционной связи необходимо, чтобы прочностные харак - ^еристики бетоной каждой такой группы Изменялись ё достаточно широком диапазоне.
Характеристика опытных данных, относящихся к рассматриваемой категории тяжелых бетонов и сгруппированных по признаку рт = const и ф = const, представлена в табл. 6.
Были проанализированы результаты 525 серий испытаний, включая результаты измерения начального модуля упругости статическим методом при напряжениях порядка о = (0,15—0,25)/?т, где Rx —кубиковая прочность бетона в момент приложения нагрузки. Несмотря на принятые ограничения в отборе этих результатов, в табл. 6 представлены данные, характеризующие большую категорию тяжелых бетонов (в том числе высокопрочных). Общее число примененных в опытах разновидностей портландцементов и заполнителей достигает соответственно 51 и 32, причем хорошо представлены современные отечественные особо быстротвердеющие портландцемента (пять различных партий). Разнообразны были методы уплотнения бетонной смеси (штыкование — группы серий 1—12, обычная вибрация или вибрация с пригрузом — группы серий 19—27, высокочастотная вибрация — группа серий 18, силовой прокат — группа серий 28) и условия твердения бетона до испытания (влажное хранение, твердение в условиях различной атмосферной влажности, тепловлажностная обработка — группы серий 19 и 21). Наряду с обычными тяжелыми бетонами на крупном заполнителе представлены мелкозернистые песчаные (группы серий 20, 21, 26—28). Наконец, в широких пределах варьировался возраст бетона в момент приложения нагрузки (как правило, от 1 до 360 суток), достигая в отдельных случаях десятков лет (группы серий 14—16).
Полученные результаты статистической обработки, которые также приведены в табл. 6, убедительно свидетельствуют о том, что в пределах каждой из групп серий испытаний наблюдается надежная корреляционная связь в форме (У. ГЗ) между модулем упругости и прочностью бетона. Коэффициенты корреляции, за редкими исключениями, находятся на очень высоком уровне (г = 0,95-^-0,99). При этом указанная форма связи обнаруживается равным образом и в зоне низких (группы серий 1, 6, 8, 22) и в зоне высоких (группы серий 18, 21, 24) прочностных показателей бетона. Таким образом, она достаточно устойчива во всем возможном в настоящее время интервале изменения
| Коли | |||||
| Со | Чество | ||||
| Автор | А о | Кубиковая | Разновидно | ||
| Эксперимен | « я | О | Прочность | Стей | |
| Тальных | О, а) о | Ш (-> О | S | ||
| Данных | О ч | О К | В кГ/см2 | Н к | К ч О к |
| О К | Ч й о о | 2 0J СГ | С ч (Я 0J M н | ||
| Уокер [202] | 32 | 160 | 50—400 | 3 | 1 |
| Джонсон | 25 | 125 | 50—450 | 5 | 1 |
| [158] | |||||
| Дютрон | 23 | 69 | 50—500 1 | ||
| [132] | 32 | 96 | 50—500 | 1 | 7 |
| 19 | 57 | 150—450 J | |||
| Сантарелла | 18 | 54 | 150—400 Ї | ||
| [190] | 39 | 117 | 150—500 | 3 | 1 |
| 11 | 33 | 150—400 J | |||
| Ричарт и | 25 | 75 | 100—300 ) | ||
| Дженсен | 25 | 75 | 100—350 | 1 | 1 |
| [186] | 25 | 75 | 150—450 J | ||
| Граф [145] | 6 | 19 | 150—450 | 3 | 1 |
| Визей и | 6 | 18 | 200—550 | 1 | 1 |
| Вендт [212] | |||||
| Уош и Флук | 8 | 16 | 100-500 | О | 1 |
| [207] | 8 | 16 | 150—700 / | Z | |
| Клигер [164] | 20 | 60 | 400-700 | 10 | 1 |
| Мамийан | 36 | 36 | 150—650 | 1 | 1 |
| [168] | |||||
| Писанко | 33 | 110 | 500—1000 | 4 | 3 |
| [15, 66] | |||||
| Улицкий | 13 | 36 | 200—500 | 2 | 2 |
| [33, 95] | 6 | 14 | 250—500 | 1 | 1 |
| Цейлон [103] | 10 | 30 | 450—800 | 3 | 1 |
| Краль [166] | 5 | 15 | 150—400 | 2 | 2 |
| 6 | 18 | 250—700 | 4 | 1 | |
| Сытник и | 8 | 24 | 600—1000) | ||
| Иванов | 36 | 108 | 50—11001 | О | U |
| ' [87, 88] | 5 5 | 15 15 | 50—500 [ 50—1200J | Z | Г |
| Цниис— | 16 | 28 | 550—850 | 1 | 1 |
| НИИЖБ | |||||
| Рокач и Ко | 8 | 8 | 250—550 ) | О | 1 |
| Четков [76] | 16 | 16 | 150—750 / | Z |
| Результаты статистической обработки |
Кубиковой прочности бетона. Примером служат, в частности, опыты Сытника и Иванова (группа серий 25).
Данные табл. 6 подтверждают также вывод о том, что форма и устойчивость корреляционных связей между Ех И Rx практически не зависят от изменчивости таких факторов, как возраст бетона в момент загружения, свойства портландцемента, гранулометрический состав заполнителей, условия уплотнения и твердения бетона и т. д. В пределах многих групп серий некоторые из этих характеристик варьировались весьма широко.
Сытник и Иванов (группа серий 25) определяли модуль упругости на бетоне в возрасте 1, 3, 7, 14, 28, 60, 90, 180, 360 суток. Клигер (группа серий 16) использовал портландцемент 10 типов самого разнообразного минералогического состава. В опытах Джонсона (группа серий 2) один и тот же заполнитель был представлен восемью разными гранулометрическими составами. В опытах Мамийана (группа серий 17) образцы твердели до начала испытания их в разном возрасте в воде и в условиях различной атмосферной влажности (99, 75, 50 и 35%).
Как видно из табл. 6, колебания этих условий в названных, а также других группах серий испытаний не отразились на разбросе опытных точек и величинах корреляционных коэффициентов. В то же время очевидно, что основное влияние на характер связи модуля упругости и прочности бетона оказывают упругие свойства заполнителя и содержание цементного теста в смеси. Это находит выражение в том, что получаемые параметры прямых регрессий А0 и Ь0, соответствующие разным группам серий, различаются весьма существенно. При этом указанное влияние проявляется в полном соответствии с выражениями (V. 13) и (V. 14).
Данные статистической обработки результатов испытаний двух групп серий (И и 30) приведены на рис. 39. Поскольку содержание цементного теста в обеих группах серий было принято одинаковое, явное различие корреляционных зависимостей может быть отнесено лишь за счет влияния упругих характеристик заполнителя. Бетонам на граните в опытах Рокача и Кочеткова (группа серий 30) соответствует, как и следовало ожидать, более низкое значение коэффициента Ь0 по сравнению с бетонами на гравии в опытах Ричарта и Дженсена (группа серий 11).
Из формулы (V.14) видно, что различие в упругих свойствах заполнителя при одинаковом расходе цементноготеста должно привести к повороту корреляционной прямой относительно точки пересечения ее с осью ординат. Поворот по часовой стрелке свидетельствует об увеличении модуля упругости заполнителя. Именно этой закономерности подчиняются зависимости, представленные на рис. 39, а также большинство аналогичных данных табл. 6.
Влияние содержания цементного теста в бетоне показано на рис. 40. Здесь сопоставлены результаты обработки опы-
Тов Дютрона (группы серий 3 и 5), относящиеся к бетонам на одинаковых заполнителях, но с разным содержанием цементного теста в смеси. При достаточно близких значениях коэффициента Ь0 большее значение параметра а0 Получено для группы серий 5 с большим содержанием цементного теста. Таким образом, как это и предполагается в соответствии с (V.14), из-за влияния рассматриваемого фактора корреляционная прямая смещается практически параллельно самой себе.
На рис. 41 обобщены данные статистической обработки результатов испытаний всех групп серий. Значения коэффициентов корреляционных прямых а0 = и ~ = ф£кт,
Взятые из табл. 6, нанесены в зависимости от содержания цементного теста в бетонной смеси рт. Там же даны анало-
Рис. 40. Влияние содержания цементного теста в бетоне на характер корреляционной связи (V.14) между модулем упругости и прочностью тяжелого бетона, по данным Дютрона [132] 1 — бетоны с рт = 0,16; у=23,1 + 0,208Х; /-=0,966; 2 —бетоны с рт= = 0,25; У = 43,7 + 0,197Х; г = 0,95 1
| Рис.41. Общие закономерности изменения коэффициентов корреляционных уравнений в форме (V.14). Тяжелые бетоны на 50 видах портландцемента различного минералогического состава и на 32 разновидностях заполнителя из прочных пород 1 — бетоны на крупном заполнителе; 2 — мелкозернистые песчаные бетоны; 3— принятая общая зависимость для коэффициента а0 |
S 1
Гичные параметры aQ = и т = £кт, полученные ра-
Нее для цементного камня (при рт = 1).
Правильность теоретических предпосылок, заложенных в выражениях (V.13) или (V.14), подтверждается рис. 41. В полном соответствии с ними величины коэффициентов а0 =
Spv
= примерно пропорциональны рт, что соответствует
Условию S = const (поскольку £кт = const). Значение постоянной S может быть оценено по тангенсу угла наклона аппроксимирующей прямой а0 = F(PT). Как видно из рис. 41, данная зависимость для бетонов и растворов в общем случае не совпадает, причем для тех и других s Ф SK, поскольку прочность чистого цементного камня, вообще говоря, отличается от его прочности в растворе или в бетоне.
Вместе с тем это несовпадение не столь существенно. Для практических оценок допустимо принимать единую зависимость а0 = /(рт)> удовлетворяющую бетонам, растворам и чистому цементному камню, т. е. положить S ^ ^ S = 800.
К І
Значения коэффициентов т - = фЕкт (см. рис. 41) прак-
Тически свидетельствуют об отсутствии их закономерной связи с количеством цементного теста рт. Это значит, что колебания параметра ф в формуле (V.13) действительно обусловлены преимущественно различием упругих свойств заполнителей. Проверить количественное влияние указанного фактора на основании результатов рассмотренных опытов не удается, поскольку отсутствуют данные о модулях упругости использованных заполнителей.
Однако можно убедиться, что зона расположения опытных точек на рис. 41 отвечает реально возможным пределам колебания модуля упругости плотных заполнителей Е3 = = (4-т-б) Ю5.
Используя в выражении (V.13) полученное ранее среднее значение S = 800, а также Ект = 5 • 105, можно записать его в окоцчательной форме:
5ср Rr
Ex • 10 —----------- ^— , (V.15)
П Еч
Где, по-прежнему, ф =-------------------------- , а п = —— .
F +рТ(п — 1) 500 000
Формула (V.15), являясь по существу полуэмпирической, применима одинаковым образом для оценки величины начального модуля упругости тяжелого бетона на крупном заполнителе, мелкозернистого песчаного бетона и чистого цементного камня. В последнем случае достаточно принять р т = 1 (и, следовательно, ф = 1) и выражение (V.15) переходит в (V.7) для цементного камня.
Кольца колодцев были и остаются очень востребованным строительным материалом. К слову, кольца колодцев приобретают не только те, чья деятельность связана с водоснабжением и канализацией, но и телефонисты, Интернет-провайдеры и, конечно …
Полученное выражение (V.15) дает возможность сформулировать общее положение о характере зависимости меж - ду упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что оца не является …
Об усадке тяжелого бетона имеется не меньше экспериментальных данных, чем о его ползучести. Попытки- использовать эти данные для получения общих количественных закономерностей явления содержатся в ряде работ. При оценке возможной …
msd.com.ua
Упругие и прочностные характеристики материалов
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела - сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.

Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k - коэффициент жесткости:
k = EF/l (318.2.3)
где l - длина образца, F - площадь сечения, Е - модуль Юнга.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε - отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
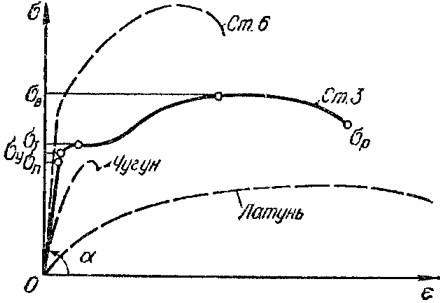
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом - углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов

Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
3. Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести - линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести - соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
В таблицах 318.2 - 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон

Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород

5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования "шейки" значительно изменяется площадь сечения образца в районе "шейки". Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
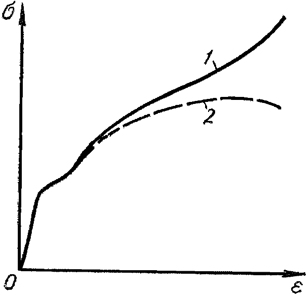
Рисунок 318.3. Диаграмма напряжений: 2 - по отношению к начальной площади поперечного сечения, 1 - по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo - F)/Fo (318.2.7)
где Fo - начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F - площадь поперечного сечения в районе "шейки". Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 - результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η - коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5
а - для пластических материалов; б - для хрупких материалов ; в - для дерева вдоль волокон, г - для дерева поперек волокон.
Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 - 318.5.
Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.
Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.
Влияние температуры на изменение механических свойств материалов
Твердое состояние - не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.
Таблица 318.6. Температуры плавления некоторых веществ

Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.

Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия - увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих - повышение предела прочности (селектрон).
doctorlom.com










