Какая пропорция пластификатора к цементу? Какая пропорция
Пропорции | Формулы с примерами
Что такое пропорция?
Определение Пропорция - это верное равенство двух отношений.

Где a ? 0, b ? 0, c ? 0, d ? 0.
a и d - называют крайними членами пропорции; b и c - называют средними членами пропорции.
Пример| 3 | = | 18 | или 3 : 5 = 18 : 30; |
| 5 | 30 |
| 7 | = | 21 | или 7 : 3 = 21 : 9; |
| 3 | 9 |
| 12 | = | 48 | или 12 : 15 = 48 : 60. |
| 15 | 60 |
Основное свойство пропорции
Свойство
Произведение крайних членов пропорции равно произведению ее средних членов.
Пример| 12 | = | 24 | , значит 12 • 8 = 4 • 24; |
| 4 | 8 |
| 11 | = | 33 | , значит 11 • 21 = 7 • 33; |
| 7 | 21 |
| 23 | = | 69 | , значит 23 • 42 = 14 • 69. |
| 14 | 42 |
Обратное свойство
Свойство Пример
Пример | 11 • 4 = 2 • 22 значит, | 11 | = | 22 | ; |
| 2 | 4 |
| 21 • 6 = 42 • 3 значит, | 21 | = | 42 | ; |
| 3 | 6 |
| 33 • 21 = 7 • 99 значит, | 33 | = | 99 | . |
| 7 | 21 |
Производные пропорции
Правило Пример
Пример | 4 | = | 8 | или | 7 | = | 14 | или | 8 | = | 17 | или | 4 | = | 7 | ; |
| 7 | 14 | 4 | 8 | 4 | 7 | 8 | 14 |
| 5 | = | 10 | или | 6 | = | 12 | или | 10 | = | 12 | или | 5 | = | 6 | ; |
| 6 | 12 | 5 | 10 | 5 | 6 | 10 | 12 |
| 9 | = | 18 | или | 3 | = | 6 | или | 6 | = | 18 | или | 9 | = | 3 | . |
| 3 | 6 | 9 | 18 | 3 | 9 | 18 | 6 |
Правило ! По трем известным членам пропорции всегда можно найтиее неизвестный член.
Пример| 15 | = | x | , значит x = | 15 • 14 | = 15 • 2 = 30; |
| 7 | 14 | 7 |
| 21 | = | x | , значит x = | 21 • 9 | = 21 • 3 = 63; |
| 3 | 9 | 3 |
| 33 | = | 99 | , значит x = | 4 • 99 | = 4 • 3 = 12. |
| 4 | x | 33 |
Отношения
Определение Отношением двух чисел a и b называется их частное a : b.
Показывает во сколько раз a больше b или какую часть число a составляет от b.1
Примеры отношений
Пример 1 Отношение числа 16 к числу 4 равно 16 : 4 = 4, т.е. 16 в 4 раза больше чем,чем 4.
Пример 2 Отношение числа 4 к числу 12 равно 4 : 12 = 13, т.е. 4 составляет третьот числа 12.
Пример 3 Масса стакана с жидкостью равна 440г. Стакан весит 40г. Какую часть всей массы составляет масса стакана? Во сколько раз масса стакана с жидкостью больше массы жидкости?Решение:
Масса стакана составляет 40 : 440 = 1 11 часть полной массы. Масса жидкости равна 440 - 40 = 400г; масса стакана с жидкостью больше массы самой жидкости в 440 : 400 = 1,1 раза.
formula-xyz.ru
Пропорция пластификатора к цементу - как рассчитать?
Для получения действительно хорошего результата в виде прочного материала, который прослужит вам не один сезон, в общую массу необходимо добавить специальные вещества, получившие название пластификаторы. Это вещества, обеспечивающие пластичность бетонной смеси, и не ухудшающие качество готового бетона.
Запомните: в домашних условиях не старайтесь приготовить раствор без пластификатора – деньги на ветер.
Какие пластификаторы бывают?
Виды пластификаторов:
- гидрофильные;
- гидрофобные.
И те, и другие повышают пластичность, текучесть готового раствора.
Плюсы использования пластификаторов:
- Повышается пластичность смеси.
- Экономия цемента.
- Повышается прочность готовых изделий в среднем на 25%.
- Не нужно использовать виброуплотнители и другие добавки для уплотнения бетонного раствора.
- Повышается текучесть готовой бетонной смеси, что способствует расширению зоны применения таких смесей.
- Повышенная водонепроницаемость готовых изделий.
- Устойчивость к низким температурам и механическим воздействиям.
Какой пластификатор выбрать, и какое количество добавить?
Строительная промышленность предлагает сегодня огромный выбор различных добавок и пластификаторов. Совсем не нужно знать их, достаточно соблюдать несколько правил.
Во-первых, выбирайте только известные марки-производители, во-вторых, подробно читайте, что написано на этикетке, и какие свойства можно ожидать. И, конечно, лучше всего приобретать состав в специализированных магазинах, имеющих все сертификаты качества на данную продукцию.
Большую обеспокоенность у многих вызывает вопрос, какая пропорция пластификатора к цементу будет создавать необходимый перечень свойств
ВАЖНО ЗНАТЬ: практически все популярные пластификаторы добавляются в бетонные смеси в виде водного раствора с различной рабочей концентрацией вещества:
- полипласт СП-1 в количестве 0,4 — 0,8% сухого вещества (400-800 г на 100 кг цемента) от массы цемента;
- пластификатор С-3 – 0,25-0,7 % (250-700 г на 100 кг цемента) от массы цемента;
- жидкое мыло — 0,5 – 1%, не более. На ведро цемента – 1-2 столовые ложки.
На самом деле, все пропорции применяемых пластификаторов зависят от области применения будущего раствора. Например, в популярном материале арболит пропорции опилок к цементу, зависят от того, какой арболит мы хотим получить на выходе: конструкционный, либо теплоизоляционный.
cemtown.ru
Пропорция
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение 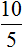 равно отношению
равно отношению 
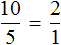
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
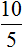
Выполнив деление в этой дроби, мы получим 2. То есть, десять девочек так будут относится к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:

Выполнив деление в этой дроби, мы снова получим 2. То есть, две девочки так будут относится к одному мальчику, что на этого одного мальчика будут приходиться две девочки.
Можно сделать вывод, что отношение 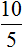 пропорционально отношению
пропорционально отношению  . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
. Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что 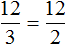 , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение 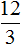 не пропорционально отношению
не пропорционально отношению 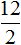 .
.
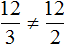
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция 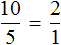 состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была 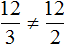 . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями
. Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями 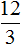 и
и 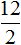 знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
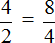
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции 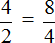 крайние члены это 4 и 4, а средние члены это 2 и 8
крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
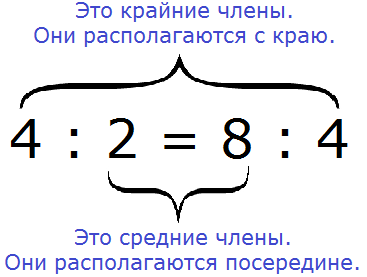
С помощью переменных пропорцию можно записать так:
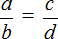
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция 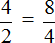 . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
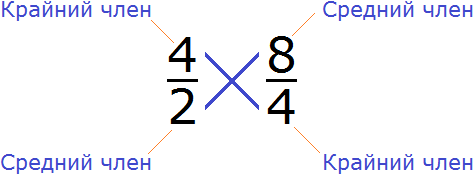
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция 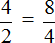 составлена правильно.
составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция 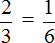
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
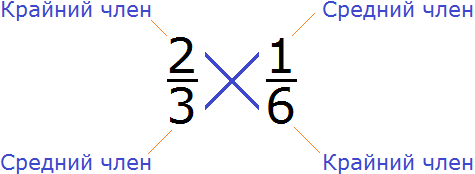
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция 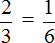 составлена неправильно.
составлена неправильно.
Поэтому в пропорции 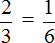 разумнее заменить знак равенства (=) на знак не равно (≠)
разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Какая пропорция цемента с песком нужна для фундамента здания
При возведении базиса под строение для приготовления бетона необходимо знать, какая пропорция цемента с песком нужна для фундамента, в каких пропорциях добавляется щебень и вода.
Цементная масса обладает вяжущими свойствами и при ее перемешивании с такими заполнителями, как песок, щебень и вода, получается раствор, который затвердевая образует крепкий стройматериал, выдерживающий многотонные нагрузки.
Чтобы улучшить качественный состав бетонного раствора, используют порции добавок, как пластификаторы и другие.
Фундаментальный бетон
Бетонный раствор представляет собой каменный материал, как результат затвердевшей бетонной смеси.
Ее состав – это смесь пропорций цементного порошка, связывающего все песчинки и камешки в единый монолит, песочного материала и гравия, являющихся заполнителями получаемого раствора, и воды.
Цементный порошок заполняет образованные между песчинками и гравием пустоты. При большом количестве подобных пустот потребуется больше цемента.

Для уменьшения количества пустот применяют наряду с крупным гравием и гравий мелкой фракции для заполнения им свободного места между большими элементами. Оставшиеся пустоты будет заполнять песочный материал.
Требуется время для застывания бетона фундамента, это даст ему возможности набраться прочности. Полностью основа затвердевает спустя месяц, его наиболее интенсивное застывание осуществляется в первые 5-7 дней.

Состав фундаментального бетона
Раствор, который используется для заливки основания здания имеет такой состав бетона.
Цементные разновидности: портландцемент, шлакопортландцементная смесь, пуццолановый портландцемент и их варианты быстрого затвердевания.
По своему природному составу они одинаковы, но каждый из них обладает рядом особенностей. Наиболее распространен портландцемент, используемый под возведение любых строений, создание монолита также возможно.

Шлакопортландцементная смесь обладает высокой влагостойкостью, но малой морозостойкостью, затвердевает медленнее.
Пуццолановый вариант идеален для строительства, отличающегося наличием высокого уровня влажности, – подводные и подземные сооружения. При его использовании на воздухе усадка такого базиса слишком большая, при этом присутствует частичная потеря прочности.
Выбор цементной марки зависит от проектной марки бетонного раствора и имеет следующие маркировки: 200, 300, 400 и т.д.
Данный показатель идет на возможный предел прочности, осуществляемый при сжатии в кг на кв. см куба из бетона с ребром 20 см после того, как он затвердеет через 28 дней. Бетонная марка должна быть в 1,5-2 раза меньше цементной марки.
Песочный материал – это мелкодисперсный заполнитель. В нем должны отсутствовать глинистые примеси, ил (их содержание не должно быть выше 5%) и растения.

Слишком большое количество ила и глины отрицательно скажется на прочности фундамента. Для бетонной смеси применяют заполнитель с песчинками от 1,2 мм до 3,5 мм, не мельче.
Чистота этого заполнителя проверяется так: он насыпается в бутылку, заливается водой и взбалтывается. Наличие прозрачной или немного мутной воды говорит о его чистоте.
Сильно мутная вода или наличие глиняного осадка при оседании песка – приготовление бетона недопустимо с использованием такого песка.
Для более детального ознакомления с составляющими бетона, посмотрите видео:
Щебень – раздробленные чистые горные породы без загрязнения землей и глиной, фракции которых должны быть 5-70 мм.
Загрязнения сказываются на ухудшении качественных характеристик производимого бетона для базиса.
Гравий выбирается чистым без большого количества глиняных примесей, фракция которого от 1 до 8 см. Такой материал служит заменителем щебня.
Чистая водопроводная вода без примесей.
Пропорция песка и цемента нужная для раствора под фундамент
Зная, какой должен быть результат и как должен быть использован бетон, производится расчет соотношения всех составляющих бетонного раствора.
Наиболее часто используется смесь в пропорциях 1:3, где 1 – это цементный порошок, а 3 – это песок. При добавлении большего количества песка, раствор приобретает большую крепость, но теряет эластичность.
Это затруднит его нанесение на поверхность и увеличит вероятность его отпадения даже при малом механическом воздействии.
На качество бетона влияет и марка цемента. Разные строительные работы требуют разной маркировки цемента. Например, при использовании состава М-100 и цемента М 400, пропорция будет 1:4.
Подготовительный этап
Для приготовления бетона потребуется подготовка следующих строительных инструментов:
- Лист металла;
- При большем замесе материала используется специальная емкость для замеса;
- Для крупного объема раствора – бетономешалка;
- Для смешивания сухих компонентов – лопата;
- Транспортировочная емкость для готового бетона.

Особенности соотношения
Функция фундамента – прием нагрузок от возведенного на нем здания, поэтому, чтобы выяснить, какая пропорция цемента с песком нужна для фундамента, в учет берутся все факторы. Отличие соотношений будет и в используемой марке.
Для строительства дома подойдет от М200, а для цементирования садовых тропинок – и М100.

Различие соотношений с учетом маркировки:
- М 200 – 1 кг цементного порошка, 2,8 кг песка и 4,8 кг щебня;
- М 250 – 1 кг цементного порошка, 2,1 кг песка и 3,9 кг щебня;
- М 400 – 1 кг цементного порошка, 1,1 кг песка и 2,5 кг щебня;
- М 450 – 1 кг цементного порошка, 2,8 кг песка и 4,8 кг щебня.
Более высокая марка – большее содержание цемента.
Советы
Для марок М 300 или М 400 требуется наполовину веса других составляющих меньше воды. Плотный раствор разбавляется водой. Консистенция бетона должна подвергаться возможности перемешивать его лопатой, прилагая при выполнении этого действия усилия.
В сыром песке имеется небольшой процент влаги. Поэтому песок должен быть подвергнут сушке или уменьшен объем воды при разбавлении раствора. К тому же, чем чище материал, тем лучше он будет схватываться с раствором.
Закупка цемента производится перед самим строительством за 1-2 недели до приготовления бетона смеси, так как он обладает высоким уровнем впитываемости влаги, из-за чего начинает портится.
Полезные советы, касающиеся пропорций составляющих бетона и правил его завешивания вы найдете в представленном видео:
Заливка фундамента желательна в теплый временной период, чтобы не пришлось нагревать воду и раствор, иначе это грозит застыванием раньше времени и скажется на потере прочности и его связи с арматурой.
sdelai-fundament.ru
Что такое пропорция | Математика
Здесь мы рассмотрим, что такое пропорция, как называются члены пропорции и основное свойство пропорции.
Определение пропорции:
Пропорция — это равенство двух отношений.
С помощью букв пропорцию записывают так:
![Rendered by QuickLaTeX.com \[a:b = c:d\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2989a14c8e6167dcd8afcc320213f3ea_l3.png)
или
![Rendered by QuickLaTeX.com \[\frac{a}{b} = \frac{c}{d}\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-947c383783d4f9c72ec308b9b3863822_l3.png)
Читают: «a относится к b как c относится к d» или «отношение a к b равно отношению c к d».
Числа a и d называют крайними членами пропорции, числа b и c — средними членами пропорции:
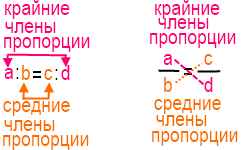
Примеры пропорций:
1) 4,8:1,6=3,6:1,2
Здесь 4,8 и 1,2 — крайние члены пропорции, 1,6 и 3,6 — средние члены пропорции.
![Rendered by QuickLaTeX.com \[2)\frac{{2,1}}{{8,4}} = \frac{{1,5}}{6}\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d3c87bfbef858213137904c41891687f_l3.png)
Здесь 2,1 и 6 — крайние члены пропорция, 8,4 и 1,5 — средние члены пропорции.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произведению ее средних членов.
![Rendered by QuickLaTeX.com \[a:b = c:d, \Rightarrow ad = bc\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-08fb585d0c73dc003ca509f799fa74ef_l3.png)
![Rendered by QuickLaTeX.com \[\frac{a}{b} = \frac{c}{d}, \Rightarrow ad = bc\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-57e0eb38329bb7710c2ea50c42d88999_l3.png)
Отсюда следует, что
![Rendered by QuickLaTeX.com \[ad = bc, \Rightarrow \frac{c}{a} = \frac{d}{b};\frac{a}{c} = \frac{b}{d}.\]](/800/600/http/www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-bb147948dcd3f1555a4f6e5d738d868b_l3.png)
Таким образом, если в пропорции поменять местами крайние члены или средние члены, то получим новые верные пропорции.
Пропорция- это равенство. Если это равенство содержит переменную, значение которой надо найти, то оно является уравнением. Как решать пропорции, мы рассмотрим в следующий раз.Кроме того, пропорции используются для решения некоторых задач. В частности, пропорции существенно облегчают решение задач на проценты. Позже мы рассмотрим также решение задач с помощью пропорций.
www.for6cl.uznateshe.ru
Составить пропорцию

Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:

что тоже самое (это разная форма записи).
Пример:

Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:

то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:


Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях "Задачи на проценты. Часть 1!" и "Задачи на проценты. Часть 2!".
2. Многие формулы заданы в виде пропорций:
> теорема синусов

> отношение элементов в треугольнике

> теорема тангенсов

> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:

Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем

Ответ: 245

Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие - x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:

То есть 50 минут это пять шестых часа.
Ответ: 5/6

Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3

Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.

Если записать отношение в общем виде, то получится

То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.
Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Пропорция (математика) — WiKi
У этого термина существуют и другие значения, см. Пропорция.Пропо́рция (лат. proportio — соразмерность, выравненность частей; определённое соотношение частей между собой), равенство отношений двух [и более] пар чисел a,b{\displaystyle a,b} и c,d{\displaystyle c,d}, т. е. равенство вида a:b=c:d{\displaystyle a:b=c:d}, или, в других обозначениях, равенство ab=cd{\displaystyle \ {\frac {a}{b}}={\frac {c}{d}}} (часто читается как: «a{\displaystyle a} относится к b{\displaystyle b} так же, как c{\displaystyle c} относится к d{\displaystyle d}»). В этом случае a{\displaystyle a} и d{\displaystyle d} называют крайними, b{\displaystyle b} и c{\displaystyle c} — средними членами пропорции. Такую пропорцию ещё называют геометрической, чтобы не путать с арифметической и гармонической пропорциями.
Основные свойства пропорций
История
Первое известное определение равных пропорций было дано как равенство последовательных вычитаний[1], современным языком это можно выразить как равенство цепных дробей для отношений величин.[2] Позже Евдокс упростил определение, равенство пропорций a:b=c:d{\displaystyle a:b=c:d} им определялось как одновременное выполнение одной из трёх пар соотношений
для любой пары натуральных чисел m{\displaystyle m} и n{\displaystyle n} . Это определение даётся в «Началах» Евклида.
С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа. Определение Евдокса, в несколько более абстрактном виде использовалось далее при определении вещественных чисел данное Дедекиндом через сечения.
Связанные определения
Задачи на тройное правило
В содержание задачи на простое тройное правило входят две величины, связанные пропорциональной зависимостью, при этом даются два значения одной величины и одно из соответствующих значений другой величины, требуется же найти её второе значение.
Задачами на сложное тройное правило называют задачи, в которых по ряду нескольких (более двух) пропорциональных величин требуется найти значение одной из них, соответствующее другому ряду данных значений величин[5][6].
Литература
- Ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. / пер. с голл. И. Н. Веселовского. — М.: ГИФМЛ, 1959.
Примечания
См. также
ru-wiki.org








.jpg)

