УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Гансена модуль упругости

Методы оценки модуля упругости

В соответствии с современными взглядами упругое деформирование бетона обусловливается структурными особенностями этого многокомпонентного материала, состоящего из цементного камня и заполнителя. Цементный камень может рассматриваться в свою очередь как многофазная система, состоящая из гелево-кристаллической массы, капиллярных пор и частиц негидратированного цемента и т. д. Соотношение этих элементов структуры в бетоне и характеристика их упругих свойств в конечном счете определяют величину деформаций бетона при кратковременном статическом нагружении. Подробный обзор существующих методов оценки модуля упругости бетона с учетом упругих свойств составляющих содержится в работе Гансена. Установлено, что достаточно общее и строгое теоретическое решение для многокомпонентной модели бетона основано на рассмотрении двухфазной системы с частицами заполнителя сферической формы, равномерно распределенными в массе цементного камня. Гансен показал, что удовлетворительные результаты могут быть получены также и в том случае, если рассматривать бетон как систему, состоящую из цементного раствора и крупного заполнителя. Исходя из этой модели, получены известные выражения для модуля упругости бетона (формулы Гансена, Шефдевиля-Дантю и т. д.). Аналитическая форма каждого выражения зависит от того, постулируется ли наличие или отсутствие полного сцепления между раствором и крупным заполнителем. В реальных условиях существует частичное сцепление между ними. Формула, предложенная Гансеном с учетом этого положения, позволяет получить результаты, приемлемо совпадающие с экспериментальными данными и вычисленными по формуле. Изложенные представления о деформировании бетона под кратковременной нагрузкой следует рассматривать как теоретическую основу для оценки этого явления. Вместе с тем возможности их практического использования для прогноза деформативности бетона ограничены, поскольку требуется знать в каждом частном случае упругие характеристики компонентов бетона. В соответствии с выражением (V.4) существует некоторое предельное значение модуля упругости бетона Ет, которое не может быть превзойдено при любом значении прочности бетона Rx. Формула (V.4) положена в основу метода оценки модуля упругости бетона в нормах СНиП, Указаниях по проектированию железобетонных мостов СН 365-67и других отечественных нормативных документах. В частности, она использована во французских нормах пректирования, а также в рекомендациях Европейского комитета по бетону, разработанных для создания международных норм проектирования железобетонных конструкций. В отличие от (V.4) формула (V.5) предполагает неограниченное возрастание модуля упругости бетона с ростом его прочности. На основании опытных данных предложены различные варианты выражений (V.4) и (V. 5), которые отличаются численными значениями коэффициентов EmtS, си v (табл. 5). Наибольшее распространение получили формулы Графа и Роша, которые сейчас широко используются при оценке упругих свойств тяжелого бетона. Как следует из табл. 5, методы прогнозирования упругой деформативности бетона основываются на уточнении коэффициентов в формулах (V.4) и (V.5) эмпирическим путем вне всякой связи с изложенными выше теоретическими представлениями. В ряде работ исследовалось влияние содержания заполнителя в бетоне, его вида и гранулометрического состава, наличия в заполнителе мелких фракций, условий твердения бетона на величину коэффициентов Ет, S, с и v. Однако применить полученные закономерности для описания одновременно большого количества экспериментальных данных не удается. Как видно из табл. 5, большинство предлагаемых коэффициентов получено для бетонов низкой или средней прочности. В какой мере эти коэффициенты пригодны для оценки модуля упругости бетонов высоких прочностей, судить трудно, поскольку экстраполяция большинства зависимостей в область прочностей порядка 1000 кГ!см2 приводит к разным результатам. Если сопоставить, к примеру, значения модулей упругости по зависимостям, принятым СНиП и рекомендациями ЕКБ (рис. 34), то наибольшие расхождения между ними (до 35%) наблюдаются именно в области высоких прочностей. Некоторые закономерности, обнаруживаемые экспериментально, вообще не поддаются объяснению на основе зависимостей (V.4) и (V.5). При измерении упругих деформаций бетонов разной прочности фиксируется в ряде случаев не возрастание, как следует из формул (V.4) и (V.5), а падение модуля с ростом прочности бетона. Это подтверждается результатами опытов Уокера Фройденталя и Ролла, а также Ричарта, Брандцига и Брауна и др. (рис. 35). Противоречия и расхождения в оценках модуля упругости бетона следует отнести, несомненно, за счет того, что существующие эмпирические зависимости не отражают влияния на его величину всех важнейших факторов. На это обстоятельство обращалось внимание в ряде работ. Таким образом, в обосновании и проверке нуждается прежде всего характер взаимосвязи упругих и прочностных свойств тяжелого бетона во всем возможном диапазоне их изменения. Это должно быть сделано путем применения имеющихся теоретических решений и статистической обработки достаточно обширной выборки опытных результатов. Только на этой основе могут быть вскрыты причины указанных противоречий и сделаны правильные выводы об упругих свойствах высокопрочных бетонов. В последние годы исследования в данном направлении проводились, в частности, в ЦНИИ. Рассмотрим основные результаты этих исследований применительно к современным тяжелым бетонам (включая высокопрочные), изготовляемым на портландцементах и заполнителях из плотных прочных пород.

vogean.com

МЕТОДЫ ОЦЕНКИ МОДУЛЯ УПРУГОСТИ БЕТОНА

ВЫСОКОПРОЧНЫЙ БЕТОН

В соответствии с современными взглядами [105, 149] упругое деформирование бетона обусловливается структурными особенностями этого многокомпонентного материала, состоящего из цементного камня и заполнителя. Цементный камень может рассматриваться в свою очередь как многофазная система, состоящая из гелево-кристалли - ческой массы, капиллярных пор и частиц негидратирован - ного цемента и т. д. Соотношение этих элементов структуры в бетоне и характеристика их упругих свойств в конечном счете определяют величину деформаций бетона при кратковременном статическом нагружении.

Подробный обзор существующих методов оценки модуля упругости бетона с учетом упругих свойств составляющих содержится в работе Гансена [149]. Установлено, что достаточно общее и строгое теоретическое решение для многокомпонентной модели бетона основано на рассмотрении двухфазной системы с частицами заполнителя сферической формы, равномерно распределенными в массе цементного камня. После некоторых преобразований соответствующее аналитическое выражение может быть представлено в виде:

Я _ + ■vK)E3/EK ^у ^

(2—vK) + VKE3JEK

Где £3 и Ек — модули упругости заполнителя и цементного камня; VK — относительное содержание цементного камня по объему в бетоне.

Предполагается при этом, что коэффициенты Пуассона Рз = І^к ^ 0,2. Генсен, оценив результаты подсчетов по формуле (V.1), обнаружил, что они вполне удовлетворительно совпадают с опытными данными.

Аналогичным путем удается получить выражение для модуля упругости цементного камня Ек, рассматривая его как систему, состоящую из гелево-кристаллической фазы с модулем упругости Еко и пор (полагая для пор Еп = 0 И Рп = 0):

<ЕК^{-=^ЕК0, (V.2)

L + fln

Где Vn — пористость цементного камня в долях по объему. По получаемым результатам это выражение близко совпадает с тем, которое было предложено в свое время Пауэр - сом [149]:

£к=(1-^п)3£ко. (V.3)

Гансен показал, что удовлетворительные результаты могут быть получены также и в том случае, если рассматривать бетон как систему, состоящую из цементного раствора и крупного заполнителя. Исходя из этой модели, получены известные выражения для модуля упругости бетона (формулы Гансена, Шефдевиля-Дантю и т. д.). Аналитическая форма каждого выражения зависит от того, постулируется ли наличие или отсутствие полного сцепления между раствором и крупным заполнителем. В реальных условиях существует частичное сцепление между ними. Формула, предложенная Гансеном с учетом этого положения, позволяет получить результаты, приемлемо совпадающие с экспериментальными'данными и вычисленными по формуле (V.1).

Изложенные представления о деформировании бетона под кратковременной нагрузкой следует рассматривать как теоретическую основу для оценки этого явления. Вместе с тем возможности их практического использования для прогноза деформативности бетона ограничены, поскольку требуется знать в каждом частном случае упругие характеристики компонентор бетона,

Поэтому при проектировании нашли широкое применение различного рода эмпирические зависимости, позволяющие предсказывать величину модуля упругости.

Наибольшее распространение получили зависимости типа:

Р D

(V.4)

S + Rx

Где Ех — модуль упругости бетона при загружении его в произвольном возрасте т; Rx — кубиковая прочность бетона в том же возрасте; Ет и S — эмпирические константы.

В соответствии с выражением (V.4) существует некоторое предельное значение модуля упругости бетона Ет, которое не может быть превзойдено при любом значении прочности бетона Rx. Формула (V.4) положена в основу метода оценки модуля упругости бетона в нормах СНиП, Указаниях по проектированию железобетонных мостов СН 365-67 [92] и других отечественных нормативных документах.

В зарубежных нормах в ряде случаев применяется степенная зависимость вида:

Ex=c(Rx)*, (V.5)

Где с и v — также некоторые эмпирические константы.

В частности, она использована во французских нормах пректирования, а также в рекомендациях Европейского комитета по бетону [96], разработанных для создания международных норм проектирования железобетонных конструкций. В отличие от (V.4) формула (V.5) предполагает неограниченное возрастание модуля упругости бетона с ростом его прочности.

На основании опытных данных предложены различные варианты выражений (V.4) и (V. 5), которые отличаются численными значениями коэффициентов Em,S, С и v (табл. 5).

Наибольшее распространение получили формулы Графа [144] и Роша [183], которые сейчас широко используются при оценке упругих свойств тяжелого бетона.

Как следует из табл. 5, методы прогнозирования упругой деформативности бетона основываются на уточнении коэффициентов в формулах (V.4) и (V.5) эмпирическим путем вне всякой связи с изложенными выше теоретическими представлениями. В ряде работ исследовалось влияние содержания заполнителя в бетоне [119], его вида и гранулометрического состава [132, 143, 202], наличия в запол-

		Кубиковая	Значения коэффициентов
Автор		Прочность*	В формулах (V.4) и (V.5)
	Ч о Uh	В кГ/см2	^т \|	S	С \|	V
Шюле.......................	1921	<200	520 000	195
Граф ........................	1923	<600	589 000	176	—	—
Рош.........................	1925	<500	550 000	187	—	—
	—	—	600 000**	300**	—	—
Иосида ....................	1930	—	700 000	310	—	—
Гуммель ..................	1935	—	555 000	200	—	—
Дженсен ....	1943	—	442 000	166	—	—
Шарма и Гупта	1960	<550	915 000	522	—	—
Дульгеру ....	1960	>600	520 000	200	—	—
СНиП.......................	—	<,600	530 000	200	—	—
	—	<600**	400 000**	200**	—	—
СН 365-67 ....	—	<600	530 000	200	—	—
Уокер .....................	1919	<400	—	—	16 800—	0,50
				18 400
Дютрон....................	1930	<650	—	—	20 500—	0,45—
				49 000	0,52
Бонцель . . ' . .	1957	—	—	—	12 250— 18 275	0,51— 0,56
Краль.......................	1966	<700	—	—	15 000—	0,50
				20 000
Кимура ...................	1967	<1200	—	—	14 200	0,48
Рекомендации
ЕКБ....................	—	<600	—	—	19 000	0,50

* Прочность бетона во всех случаях приведена к эквивалентной кубико - вой прочности.

** Данные относятся к цементно-песчаным растворам.

Нителе мелких фракций [202], условий твердения бетона [153] на величину коэффициентов Ет, S, с и v.

Однако применить полученные закономерности для описания одновременно большого количества экспериментальных данных не удается.

Как видно из табл. 5, большинство предлагаемых коэффициентов получено для бетонов низкой или средней прочности. В какой мере эти коэффициенты пригодны для оценки модуля упругости бетонов высоких прочностей, судить трудно, поскольку экстраполяция большинства зависимостей в область прочностей порядка 1000 кГ/см2 приводит к разным результатам. Если сопоставить, к примеру, значения модулей упругости по зависимостям, принятым СНиП и рекомендациями ЕКБ (рис. 34), то наибольшие расхождения между ними (до 35%) наблюдаются именно в области высоких прочностей.

Некоторые закономерности, обнаруживаемые экспериментально, вообще не поддаются объяснению на основе зависимостей (V.4) и (V.5). При измерении упругих деформаций бетонов разной прочности фиксируется в ряде случаев не возрастание, как следует из формул (V.4) и (V.5), а падение модуля с ростом прочности бетона. Это

Подтверждается результатами опытов Уокера [202] Фрой - денталя и Ролла [138], а также Ричарта, Брандцига и Брауна [185] и др. (рис. 35).

Противоречия и расхождения в оценках модуля упругости бетона следует отнести, несомненно, за счет того, что существующие эмпирические зависимости не отражают влияния на его величину всех важнейших факторов. На это обстоятельство обращалось внимание в ряде работ [17, 98, 119, 129].

Таким образом, в обосновании и проверке нуждается прежде всего характер взаимосвязи упругих и прочностных свойств тяжелого бетона во всем возможном диапазоне их изменения. Это должно быть сделано путем применения имеющихся теоретических решений и статистической обработки достаточно обширной выборки опытных результатов. Только на этой основе могут быть вскрыты причины указанных противоречий и сделаны правильные выводы об упругих свойствах высокопрочных бетонов.

В последние годы исследования в данном направлении проводились, в частности, в ЦНИИС [17, 192]. Рассмотрим основные результаты этих исследований применительно к со-

Временным тяжелым бетонам (включая высокопрочные), изготовляемым на портландцементах и заполнителях из плотных прочных пород.

Кольца колодцев были и остаются очень востребованным строительным материалом. К слову, кольца колодцев приобретают не только те, чья деятельность связана с водоснабжением и канализацией, но и телефонисты, Интернет-провайдеры и, конечно …

Полученное выражение (V.15) дает возможность сформулировать общее положение о характере зависимости меж - ду упругими и прочностными свойствами тяжелого бетона. Особенность этой связи заключается в том, что оца не является …

Об усадке тяжелого бетона имеется не меньше экспериментальных данных, чем о его ползучести. Попытки- использовать эти данные для получения общих количественных закономерностей явления содержатся в ряде работ. При оценке возможной …

msd.com.ua

Моделирование линейных упругих материалов — насколько это сложно?

Наиболее основополагающей моделью материала в механике сплошных сред является модель линейной упругой среды. Как не банально это звучит, но некоторые важные особенности этой модели могут быть не очевидны с первого взгляда. В данной статье мы углубимся в теорию и прикладные аспекты применения этой модели среды и дадим представление об изотропии и анизотропии, допустимых значениях свойств материалов, несжимаемости и влиянии геометрической нелинейности.

Изотропная линейная упругая среда

В подавляющем большинстве случаев при моделировании, включающем применение линейных упругих материалов, имеют дело с изотропной средой, упругие свойства которой не зависят от направления. Для описания такого материала требуется лишь два независимых параметра, определяющих свойства материала. Существует много разных способов выбора этих параметров, однако некоторые из них более популярны, чем другие.

Модуль Юнга, модуль сдвига и коэффициент Пуассона

Модуль Юнга, модуль сдвига и коэффициент Пуассона — наиболее часто встречающиеся в таблицах параметры, описывающие упругие свойства материалов. Они не являются независимыми, так как модуль сдвига, G, связан с модулем Юнга, E, и коэффициентом Пуассона, \nu, соотношением

G = \frac{E}{2(1+\nu)}

Модуль Юнга может быть непосредственно измерен в эксперименте по одноосному растяжению, тогда как модуль сдвига измеряется, например, в эксперименте чистого кручения.

Помимо этого, при одноосном растяжении коэффициент Пуассона определяет, насколько материал будет усаживаться (или, возможно, уширяться) в поперечном направлении. Допустимый диапазон значений составляет -1 <\nu< 0.5, где положительные значения указывают на то, что материал становится тоньше при растяжении. Есть несколько материалов, называемых Ауксетиками, которые имеют отрицательный коэффициент Пуассона. Пробка в винной бутылке имеет коэффициент Пуассона близкий к нулю, так что ее диаметр практически не изменяется вне зависимости от того, вытягивают ее или проталкивают.

Для многих металлов и сплавов \nu \approx1/3, и модуль сдвига, таким образом, составляет около 40% от модуля Юнга.

С учетом возможных значений \nu допустимые значения отношения модуля сдвига к модулю Юнга лежат внутри интервала

\frac{1}{3} < \frac{G}{E} < \infty

Когда значение \nu приближается к 0.5, материал становится несжимаемым. При анализе таких материалов возникают специфические проблемы, которые мы обсудим ниже.

Модуль объемной упругости

Модуль объемной упругости, K, определяет изменение объема при заданном равномерном сдавливании. Выраженный через E и \nu, он запишется в виде:

K = \frac{E}{3(1-2\nu)}

Когда \nu= 1/3, значение модуля объемной упругости равно значению модуля Юнга, но для несжимаемого материала (\nu \to0.5), K стремится к бесконечности.

Модуль объемной упругости обычно задается вместе с модулем сдвига. Эти две величины являются, в некотором смысле, более физически независимыми параметрами. Изменение объема материала определяется только модулем объемной упругости, тогда как искажение его формы — только модулем сдвига.

Параметры Ламе

Параметры Ламе́ (коэффициенты Ламе, константы Ламе, постоянные Ламе, упругие постоянные Ламе, модули упругости Ламе) \mu и \lambda в основном используются для математического описания явлений упругости. Полная система 3-х мерных материальных соотношений между тензором напряжений \boldsymbol \sigma и тензором деформаций \boldsymbol \varepsilon (в случае однородной изотропной упругой среды) может быть записана в компактной форме с помощью параметров Ламе в виде:

\boldsymbol \sigma=2\mu \boldsymbol \varepsilon +\lambda \; \mathrm{trace}(\boldsymbol{\varepsilon}) \mathbf I

Параметр \mu является просто модулем сдвига, тогда как параметр \lambda может быть представлен как

\lambda = \frac{E \nu}{(1+\nu)(1-2\nu)}

Полную таблицу преобразований между различными упругими параметрами можно посмотреть здесь.

Несжимаемость линейных упругих материалов

Некоторые материалы, такие как, например, резина, являются практически несжимаемыми. С математической точки зрения полностью несжимаемый материал принципиально отличается от сжимаемого. В силу того, что отсутствует изменение объема, теперь не представляется возможным определить среднее напряжение. Уравнения состояния для среднего напряжения (давления), p, как функции изменения объема, \Delta V, в виде

p = f(\Delta V)

более не существует, и вместо этого оно должно быть заменено на ограничение, констатирующее, что

\Delta V = 0

Другой подход к проблеме несжимаемости следует из факта, что член (1-2\nu) появляется в знаменателе материальных уравнений, так что деление на ноль может произойти только при условии \nu= 0.5. Не попробовать ли, в таком случае, смоделировать несжимаемый материал приблизительно, установив значение \nu= 0.499?

Это можно сделать, но в данном случае, стандартное смещение узлов сетки, полученное на основе формализма метода конечных элементов, может привести к неожиданным результатам. Это вызвано явлением, называемым блокирование. Возможные эффекты:

чрезмерно жесткие модели;
«шахматная» картина напряжений;
сообщения об ошибках или предупреждения от решателя о плохой обусловленности системы уравнений.

Коррекция результатов возможна при использовании смешанной формулировки, в которой давление вводится в качестве дополнительной степени свободы. В среде COMSOL Multiphysics, включить смешанную формулировку можно, выбрав пункт Почти несжимаемый материал в настройках модели материала.

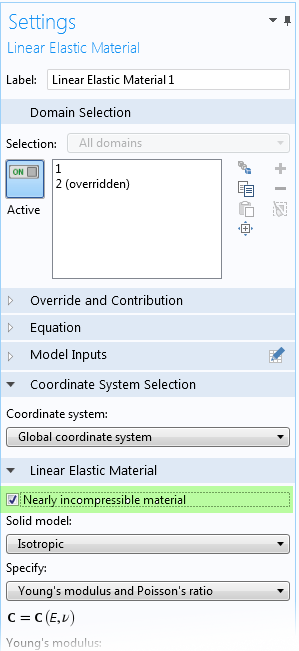nearly incompressible material Моделирование линейных упругих материалов насколько это сложно? Часть настроек модели линейного упругого материала, с включенной поддержкой смешанной формулировки.

При величине коэффициента Пуассона большей, чем 0,45 (но, естественно, не большей 0,5), или когда модуль объемной упругости более чем на порядок превышает модуль сдвига, целесообразно использовать смешанную формулировку. Эффект от ее использования показан на рисунке ниже.

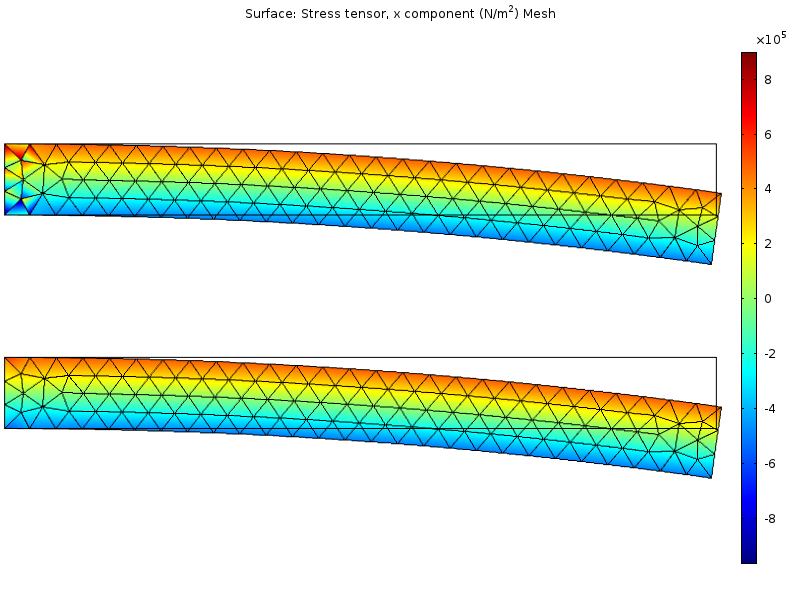stress distribution in plane strain model Моделирование линейных упругих материалов насколько это сложно? Распределение напряжений в простой модели плоских деформаций, \nu = 0.499. Верхнее изображение показывает решение, основанное на стандартной формулировке, тогда как нижнее относится к смешанной формулировке.

В решении, использующем в качестве степеней свободы только смещения узлов, картина распределения напряжений обнаруживает искажения в левой части, где имеется ограничение. Эти искажения практически полностью устраняются при использовании смешанной формулировки.

Ортотропия и анизотропия

В общем случае свойства линейных упругих материалов зависят от направления. В наиболее общем случае анизотропного материала это означает, что все шесть компонент тензора напряжений могут зависеть от всех шести компонент тензора деформации. Для описания этого требуется 21 материальный параметр. Ясно, что получение всех этих данных в эксперименте является очень непростой задачей. Если напряжение, \boldsymbol \sigma, и деформацию, \boldsymbol\varepsilon, трактовать как 6-ти мерные векторы (по числу независимых компонент тензора), они будут связаны между собой посредством 6х6 симметричной матрицы материальных параметров \mathbf D

\boldsymbol \sigma= \mathbf D \boldsymbol \varepsilon

К счастью, как правило, неизотропные материалы обладают определенной симметрией. В частном случае ортотропного материала, есть три выделенных ортогональных направления, в которых сдвиг отделяется от осевого действия. То есть, растягивание материала вдоль одного из этих главных направлений, приведет только сжатию (без сдвига) в двух других ортогональных направлениях. Полное описание ортотропного материала требует девяти независимых материальных параметров.

Материальные соотношения в ортотропном материале легче воспринимаются, когда они записаны в виде матрицы податливости (обратной к матрице упругих модулей), \boldsymbol \varepsilon= \mathbf C \boldsymbol \sigma:

\mathsf{C} =\begin{bmatrix}\tfrac{1}{E_{\rm X}} & -\tfrac{\nu_{\rm YX}}{E_{\rm Y}} & -\tfrac{\nu_{\rm ZX}}{E_{\rm Z}} & 0 & 0 & 0 \\-\tfrac{\nu_{\rm XY}}{E_{\rm X}} & \tfrac{1}{E_{\rm Y}} & -\tfrac{\nu_{\rm ZY}}{E_{\rm Z}} & 0 & 0 & 0 \\-\tfrac{\nu_{\rm XZ}}{E_{\rm X}} & -\tfrac{\nu_{\rm YZ}}{E_{\rm Y}} & \tfrac{1}{E_{\rm Z}} & 0 & 0 & 0 \\0 & 0 & 0 & \tfrac{1}{G_{\rm YZ}} & 0 & 0 \\0 & 0 & 0 & 0 & \tfrac{1}{G_{\rm ZX}} & 0 \\0 & 0 & 0 & 0 & 0 & \tfrac{1}{G_{\rm XY}} \\\end{bmatrix}

Поскольку матрица податливости должна быть симметричной, то двенадцать независимых используемых параметров (ненулевых компонентов) сокращаются до девяти, с помощью трех соотношений симметрии типа

\tfrac{\nu_{\rm YX}}{E_Y} = \tfrac{\nu_{\rm XY }}{E_X}

Обратите внимание, что \nu_{\rm YX} \neq \nu_{\rm XY}, поэтому при работе с ортотропными данными необходимо быть уверенным в том, что используется значение нужного коэффициента Пуассона. В разных источниках обозначения и, соответственно, значения могут различаться.

Анизотропия и ортотропия обычно возникают в неоднородных материалах. Зачастую эти свойства не измеряются, а вычисляются с помощью процесса гомогенизации, когда микроскопические свойства масштабируются до макроскопического уровня. (Суть процесса заключается в усреднении микроскопических уравнений — уравнений, описывающих поведение и свойства одной микрочастицы — по макроскопическому объему, выявляя и сохраняя при этом свойства, которые характеризуют, как индивидуальную микрочастицу, так и весь ансамбль микрочастиц в целом.) Обсуждение такой гомогенизации, правда в несколько ином контексте, можно найти в данной блог-статье.

Для неизотропных материалов имеются ограничения на допустимые значения материальных параметров, аналогичные описанным для изотропных материалов. Затруднительно в явном виде продемонстрировать эти ограничения, но есть две вещи, на которые стоит обратить внимание:

матрица материальных параметров \mathbf D должна быть положительно определенной;
1. для произвольного анизотропного материала достаточно проверить, что все собственные значения матрицы положительно определенные величины;
2. для ортотропного материала это справедливо, если все шесть упругих модулей положительны, и выполняется неравенство \nu_{\rm XY}\nu_{\rm YX}+\nu_{\rm YZ}\nu_{\rm ZY}+\nu_{\rm ZX}\nu_{\rm XZ}+\nu_{\rm YX}\nu_{\rm ZY}\nu_{\rm XZ}<1
если материал обладает низкой сжимаемостью, то необходимо применять смешанную формулировку;
1. для этого можно оценить эффективный модуль объемной упругости и сравнить со значениями модулей сдвига;
2. в случае неопределенности лучше перестраховаться и затратить лишние ресурсы на смешанную формулировку, чтобы избежать возможных неточностей.

Геометрическая нелинейность

При решении геометрически нелинейных задач значение термина “линейная упругость” в действительности является вопросом соглашения. Проблема состоит в том, что существует несколько возможных представлений для описания напряжений и деформаций. Обсуждению различных мер деформаций и напряжений посвящена предыдущая блог-статья.

Так как в качестве исходных величин напряжений и деформаций в среде COMSOL Multiphysics приняты второй тензор напряжений Пиола-Кирхгофа и тензор меры деформации Грина-Лагранжа, то естественное свойство линейной упругости состоит в том, что эти величины имеют линейную зависимость друг относительно друга. Такой материал иногда называют материалом Сен-Венана.

Интуитивно можно предположить, что термин “линейная упругость” означает существование линейной зависимости между прикладываемой силой и смещением в простом эксперименте по растяжению. Однако это не так, поскольку и напряжения, и деформации изменяются по мере растяжения. Чтобы показать это, рассмотрим стержень с квадратным поперечным сечением.

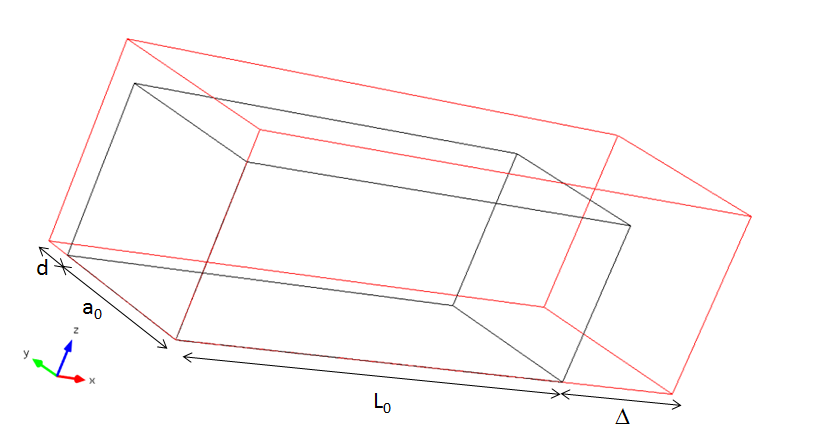bar uniform extension Моделирование линейных упругих материалов насколько это сложно? Стержень, подвергнутый равномерному растяжению.

Исходная длина стрежня равна L_0, и первоначальная площадь поперечного сечения составляет A_0=a_0^2, где a_0 — сторона начального сечения. Предположим, что стержень удлиняется на величину \Delta, так что текущая его длина составляет L=L_0+\Delta=L_0(1+\xi)

Здесь 1+\xi — это осевое растяжение и \xi можно рассматривать как относительное удлинение. Новая длина стороны в поперечном сечении будет равна a=a_0+d=a_0(1+\eta), где \eta — относительное удлинение в поперечном направлении.

Сила может быть выражена через составляющую тензора напряжения Коши \sigma_x в осевом направлении, помноженную на текущую площадь поперечного сечения:

F = \sigma_x A = \sigma_x A_0 (1+\eta)^2

Чтобы использовать линейную упругую зависимость тензоров напряжения и деформации, тензор напряжение Коши \boldsymbol \sigma необходимо выразить через второй тензор напряжения Пиола-Кирхгофа \mathbf S с помощью преобразования вида

\mathbf \sigma = J^{-1} \mathbf F \mathbf S \mathbf F^T

где \mathbf F — тензор градиента деформации, а масштабирование объема определяется J = det(\mathbf F) якобианом перехода из одной системы координат в другую. Опуская детали, для одноосного случая получим

\sigma_x = \frac{F_{xX}}{F_{yY}F_{zZ}}S_X= \frac{(1+\xi)}{(1+\eta)^2}S_X

Так как для материала Сен-Венана при одноосном растяжении осевое напряжение связано с осевой деформацией как S_X = E \epsilon_X, получаем

F = S_x A_0 (1+\xi) = E A_0 (1+\xi)\varepsilon_X

С учетом того, что осевой член тензора деформации Грина-Лагранжа определяется выражением

\varepsilon_X = \frac{\partial u}{\partial X} + \frac{1}{2}(\frac{\partial u}{\partial X})^2 = \xi+\frac{1}{2}\xi^2

выражение для силы в зависимости от смещения преобразуется к виду

F = E A_0 (1+\xi)(\xi + \frac{1}{2}\xi^2)=E A_0 (\xi+\frac{3}{2}\xi^2+\frac{1}{2}\xi^3)

Мы видим, что с учетом геометрической нелинейности линейный упругий материал в действительности подразумевает кубическую зависимость между силой и относительным удлинением (или силы от смещения, поскольку \Delta =L_0\xi), как показано на рисунке ниже.

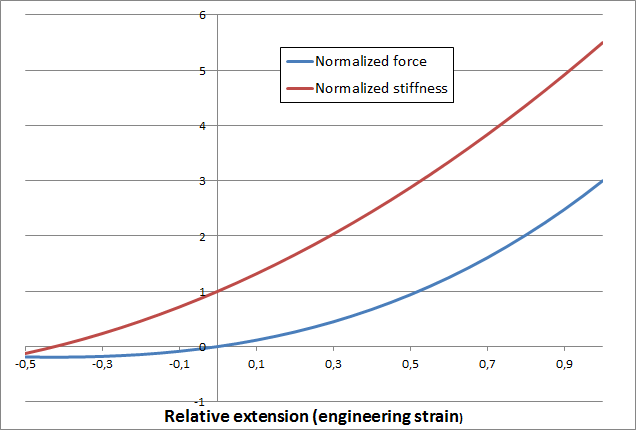uniaxial response of linear elastic material Моделирование линейных упругих материалов насколько это сложно? Одноосный отклик линейного упругого материала, обусловленный геометрической нелинейностью.

Как видно из графика, жесткость материала стремится к нулю со стороны сжатия, \xi = \sqrt{{1}/{3}}-1 \approx -0.42. На практике это означает, что моделирование при такой степени деформации будет бессмысленным. На самом деле это не является проблемой, так как можно смело утверждать, что не существует реальных материалов, которые остаются линейными при таких больших деформациях. Однако модели линейных упругих материалов зачастую используются далеко за пределами разумного диапазона напряжений по нескольким причинам, среди которых можно выделить следующие:

часто требуется быстро оценить что-нибудь «по порядку величины», прежде чем использовать более сложную модель материалов;
в модели есть сингулярности, которые вызывают очень высокие деформации в некоторых точках;
- более подробно о сингулярностях можно посмотреть здесь.
в исследовании контактных задач всегда проявляется геометрическая нелинейность;
- зачастую в ходе анализа высокий уровень сжимающих напряжений (а, следовательно, и деформаций) появляется локально на какое-то время в зоне соприкосновения материалов.

www.comsol.ru

Упругие деформации. Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.

clip_image002[4] Все тела деформируемы. Изменения, вызванные действиями приложенных сил, при которых тела меняют форму и объем – деформации.

Упругие деформации – деформации, которые исчезают, после прекращения действия приложенной силы.

Пластические деформации (остаточные деформации) – деформации, которые сохраняются в теле (частично или полностью) после прекращения действия приложенной силы.

Если напряжение (сила, отнесенная к единице площади) не превышает некоторой величины (предел упругости), то деформация будет упругой.

Идеально упругие тела – тела, которые могут претерпевать только упругие деформации. Для таких тел существует однозначная зависимость между силами и вызываемыми ими деформациями.

Малые деформации – деформации, которые подчиняются закону Гука, согласно которому деформации пропорциональны силам, их вызывающим. Все тела делятся на изотропные (свойства по всем направлениям одинаковы) и анизотропные (свойства в разных направлениях не одинаковы).

Пусть есть два стержня. Один сжимаем, а другой сдавливаем с силой clip_image004[10] (как на рисунке). Перпендикулярно к оси стержня проведем сечение clip_image006[4] . Для равновесия стержня clip_image008[4] , на его нижнее основание должна действовать сила clip_image010[4] . Нижняя и верхняя части стержня действуют друг на друга с равной силой clip_image004[11] , т.к. они деформированы. Отношение силы к площади поперечного сечения – напряжение.

Натяжение – напряжение при натяжении, clip_image013[4] .

Давление – напряжение при сжатии clip_image015[4] , где clip_image017[4] площадь сечения. Давление – отрицательное напряжение и наоборот clip_image019[4] .

clip_image021[4] – длина недеформированного стержня. clip_image023[4] – приращение длины, после приложения силы clip_image004[12] . Значит полная длина clip_image025[4] . clip_image027[4] – относительное удлинение стержня (если clip_image029[4] – относительное сжатие).

Для малых упругих деформаций натяжение clip_image031[4] (давление clip_image033[4] ) пропорционально относительному удлинению (относительному сжатию) — clip_image035[4] ( clip_image037[4] ),

где clip_image039[4] – модуль Юнга (постоянная, зависящая только от материала стержня и его физического состояния).

Модуль Юнга – натяжение, которое необходимо приложить к стержню, чтобы его длина увеличилась в два раза. А две формулы выше – закон Гука.

Вычислим упругую энергию растянутого стержня. Приложим к стержню растягивающую силу clip_image041[4] и будем постепенно (непрерывно и медленно) увеличивать ее от clip_image043[4] до clip_image045[4] . Удлинение будет меняться от clip_image047[4] до clip_image049[6] . По закону Гука clip_image051[4] ,

где clip_image053[4] – коэффициент упругости.

Вся работа по растяжению стержня пойдет на увеличение его упругой энергии clip_image055[4] . Т.к. в конечном состоянии clip_image049[7] , то clip_image058[4] , то для энергии получим clip_image060[4] .

Под действием растягивающей или сжимающей силы clip_image004[13] изменяются не только продольные, но и поперечные размеры стержня. Если сила растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. clip_image063[4] – толщина стержня до деформации (диаметр, если стержень круглый, одна из сторон, если прямоугольный). clip_image065[4] – толщина стержня после деформации. Если растягиваем стержень, то clip_image067[4] – относительное поперечное сжатие ( clip_image069[4] ).

clip_image071[4] – коэффициент Пуассона.

Он зависит только от материала рассматриваемого тела. Модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства изотропного материала. Все остальные упругие деформации можно выразить через эти коэффициенты.

Post Views: 1 867

Похожее

optoelectrosys.ru

Модуль Юнга — WiKi

Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению, сжатию при упругой деформации[1].

Размерность Единицы измерения СИ СГС

Модуль Юнга
E{\displaystyle E}
L−1MT−2
Па
дин·см-2

Назван в честь английского физика XIX века Томаса Юнга.

В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.

В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.

Модуль Юнга рассчитывается следующим образом:

E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}

где:

F{\displaystyle F} — нормальная составляющая силы,
S{\displaystyle S} — площадь поверхности, по которой распределено действие силы,
l{\displaystyle l} — длина деформируемого стержня,
Δl{\displaystyle \Delta l} — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l{\displaystyle l}).

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:

c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}

где ρ{\displaystyle \rho } — плотность вещества.

Содержание

Температурная зависимость модуля упругости простых кристаллических материалов объясняется, исходя из того, что модуль упругости M(T){\displaystyle M(T)} определяется как вторая производная от внутренней энергии W(T){\displaystyle W(T)} по соответствующей деформации E(T)=d2W(T)dε2{\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}} . Поэтому при температурах T≤ΘD{\displaystyle T\leq \Theta _{D}} (ΘD{\displaystyle \Theta _{D}} - температура Дебая) температурная зависимость модуля упругости определяется простым соотношением

M(T)=M0−M1T−M2T2{\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}

где M0{\displaystyle M_{0}} - адиабатический модуль упругости идеального кристалла при T⟶0K{\displaystyle T\longrightarrow 0K} ; M1T{\displaystyle M_{1}T} - дефект модуля, обусловленный тепловыми фононами; M2T2{\displaystyle M_{2}T^{2}} - дефект модуля, обусловленный тепловым движением электронов проводимости [2]

ru-wiki.org

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.

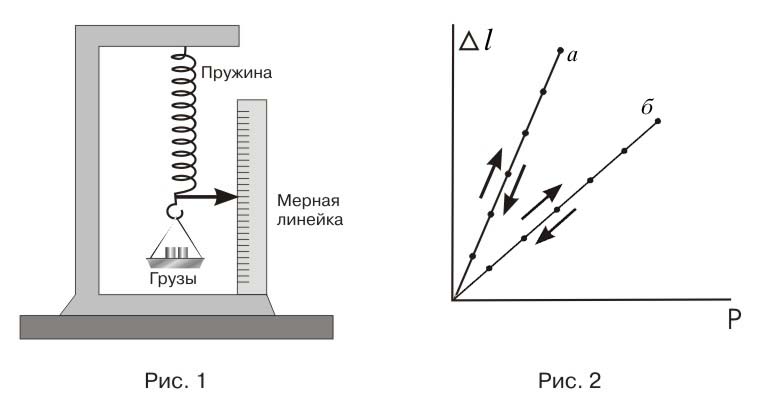
При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение Dl, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.

Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.3). Эти графики называются характеристиками пружины.

Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины Dl = P / C

Жесткость пружины С имеет размерность кг / см\up122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.

В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.

Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.

При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.

Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос. Эти примеры доказывают, что проявление упругих свойств было давно известно и давно использовалось людьми. Но понимание того, что любое твердое тело под действием даже небольших нагрузок обязательно деформируется, хотя и на очень малую величину, впервые появилось в 1660 у Роберта Гука, современника и коллеги великого Ньютона. Гук был выдающимся ученым, инженером и архитектором. В 1676 он сформулировал свое открытие очень кратко, в виде латинского афоризма: «Ut tensio sic vis», смысл которого состоит в том, что «какова сила, таково и удлинение». Но опубликовал Гук не этот тезис, а только его анаграмму: «ceiiinosssttuu». (Таким образом тогда обеспечивали приоритет, не раскрывая сути открытия.)

Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т.п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.

Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение Dl разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e.

Теперь закон Гука о пропорциональности можно записать в виде:

s = Еe

Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.

Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.

В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.

Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:

Сталь	20·104
Медь	10·104
Алюминий	7·104
Стекло	7·104
Кость	3·104
Дерево	1·104
Резина*	0,001·104

Физическая природа упругости связана с электромагнитным взаимодействием (в том числе с силами Ван-дер-Ваальса в решетке кристалла). Можно считать, что упругие деформации связаны с изменением расстояния между атомами.

Упругий стержень имеет еще одно фундаментальное свойство – утоньшаться при растяжении. То, что канаты при растяжении становятся тоньше, было известно давно, но специально поставленные опыты показали, что при растяжении упругого стержня всегда имеет место закономерность: если измерить поперечную деформацию e', т.е. уменьшение ширины стержня db , деленное на первоначальную ширину b, т.е.

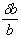
и разделить ее на продольную деформацию e, то это отношение остается постоянным при всех значениях растягивающей силы P, то есть

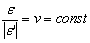
(Полагают, что e'< 0 ; поэтому используется абсолютная величина). Константа v называется коэффициентом Пуассона (по имени французского математика и механика Симона Дени Пуассона) и зависит только от материала стержня, но не зависит от его размеров и формы сечения. Величина коэффициента Пуассона для разных материалов изменяется от 0 (у пробки) до 0,5 (у резины). В последнем случае объем образца в процессе растяжения не изменяется (такие материалы называются несжимаемыми). Для металлов значения различны, но близки к 0,3.

Модуль упругости E и коэффициент Пуассона вместе образуют пару величин, которые полностью характеризуют упругие свойства любого конкретного материала (имеются в виду изотропные материалы, т.е. такие, у которых свойства не зависят от направления; пример древесины показывает, что это не всегда так – ее свойства вдоль волокон и поперек волокон сильно различаются. Это – анизотропный материал. Анизотропными материалами являются монокристаллы, многие композиционные материалы (композиты) типа стеклопластика. Такие материалы тоже в известных пределах обладают упругостью, но само явление оказывается значительно более сложным).

Если от рассмотрения растяжения стержня перейти к рассмотрению некоторого упругого тела, подверженного действию заданных сил, то следует выбрать некоторую точку M и перейти к рассмотрению ее малой окрестности в виде параллелепипеда с ребрами, параллельными координатным осям XYZ. Как известно (см. ДЕФОРМАЦИЯ), на гранях параллелепипеда действуют напряжения, которые задаются тензором s, что приводит к деформациям, которые задаются тензором e.

В общем случае закон Гука устанавливает связь между компонентами этих тензоров, которую можно записать в виде:

, ,

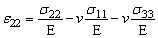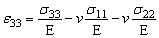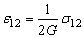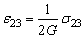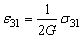
В последние три уравнения входит величина G, которая называется модулем сдвига и выражается через E и v по формуле:

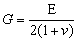
Модуль сдвига можно непосредственно определить из опыта на кручение круглого образца.

В физике для идеального газа вводится уравнение состояния (уравнение Клапейрона – Менделеева). Можно сказать, что закон Гука – это уравнение состояния для идеально упругого тела.

Владимир Кузнецов

www.krugosvet.ru

модуль упругости

модуль упругости иначе модуль Юнга (англ. elastic modulus) — коэффициент пропорциональности, связывающий напряжения и деформации в теле.

Описание

Тело, находящееся в состоянии упругого сжатия, растяжения или сдвига, характеризуется тем, что величина его деформации зависит только от величины приложенных к нему напряжений и не зависит от последовательности их приложения. Упругие деформации тела являются обратимыми: при снятии приложенных к нему нагрузок оно возвращается в начальное состояние. В области малых деформаций зависимость величины деформации от нагрузки является линейной функцией (состояние линейной упругости).

В простом случае деформации растяжения удлинение образца в направлении растяжения прямо пропорционально усилию, приложенному к телу. Коэффициент пропорциональности между удлинением образца и усилием, приложенным к нему, поделенный на площадь основания образца, называется модулем Юнга (E) данного материала. Для описания поведения линейно упругого тела также используется коэффициент Пуассона (

), который является отношением величины деформации в направлении, перпендикулярном оси растяжения/сжатия, к величине деформации вдоль этой оси при чистом растяжении/сжатии, взятым со знаком минус. Для несжимаемого тела коэффициент Пуассона равен 0,5. Дополнительно применяют следующие коэффициенты: модуль сдвига, или модуль жесткости (G или

), модуль объемного сжатия, или модуль объемной упругости (K), продольный модуль (M). Для полного описания поведения изотропного линейно упругого тела достаточно взять два любых параметра из вышеперечисленных. В общем случае линейной упругости анизотропного тела деформации задаются тензором второго ранга — тензором деформаций, зависимость которого от величин механического напряжения, заданных тензором напряжений, можно определить с помощью тензора упругости — тензора четвертого ранга, содержащего 21 независимый коэффициент.

Авторы

Горячева Ирина Георгиевна
Шпенёв Алексей Геннадьевич

Источники

Черных К.Ф. Нелинейная упругость // Математическое моделирование систем и процессов. 2001. №9. С. 177–185.
Ландау Л. Д., Лифшиц Е.М. Теоретическая физика. Т. VII. Теория упругости — М.: Наука, 1987. — 248 с.

thesaurus.rusnano.com