Расчет железобетонной балки таврового сечения. Балки железобетонные таврового сечения
Расчет железобетонной балки таврового сечения
Теоретические основы расчета
Согласно СНиП 2.03.01-84 и СП 52-101-2003 расчет тавровых поперечных сечений без арматуры в сжатой зоне рекомендуется выполнять с использованием следующих положений:
1. а) Если нейтральная плоскость (граница между сжимаемой и растягиваемой зонами сечения) проходит в полке (рисунок 326.1.а), т.е. соблюдаются условия:
RsAs < Rbb'fh'f(326.1.1)
M ≤ Rbb'fh'f(ho - 0.5h'f) (326.1.2)
и
ξ = у/ho < ξR (220.6.1)
то расчет производится, как для балки прямоугольного сечения с шириной b'f. Подробности расчета по такому алгоритму подробно расписаны в статье "Расчет железобетонной плиты перекрытия". Здесь же приведу только основные формулы:
ξR - предельно допустимое значение относительной высоты сжатой зоны бетона, определяемое по следующей формуле:
(220.6.2)
где Rs - расчетное сопротивление арматуры в МПа. Также предельное значение относительной высоты сжатой зоны бетона можно определить по таблице:
Таблица 220.1. Граничные значения относительной высоты сжатой зоны бетона
Примечание: При выполнении расчетов не профессиональными проектировщиками, ограничивающимися только расчетами по первой группе предельных состояний, я рекомендую занижать предельное значение относительной высоты сжатой зоны ξR (и значение аR) в 1.3-1.5 раза. В связи с этим возможный вариант расчета, когда y > ξRho, далее не рассматривается.
При определении сечения арматуры сначала определяется коэффициент am:
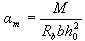(220.6.6)
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
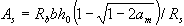(220.6.7)
В формулах (220.6.6) и (220.6.7) значения b заменяются на b'f.
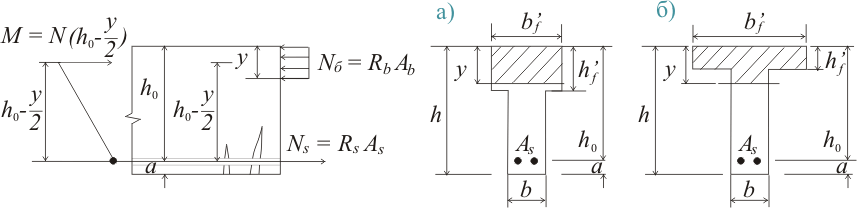
Рисунок 326.1
1. б) Если нейтральная плоскость проходит в ребре балки (рисунок 326.1.б), то расчет выполняется, исходя из следующего условия:
M < Rbbу (h0 - 0,5у) + Rbh'f(b'f - b)(h0 - 0.5h'f) (326.2)
где (b'f - b)h'f = Aov - площадь сечения свесов полки.
При этом высота сжатой зоны у определяется, исходя из следующих формул:
RsAs = Rbby + Rbh'f(b'f - b) (326.3.1)
y = (RsAs - RbAov)/Rbb (326.3.2)
при этом высота сжатой зоны принимается у ≤ ξRho.
При определении сечения арматуры сначала определяется коэффициент am:
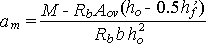(326.4.1)
при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.1 (см. выше).
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
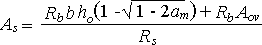(326.4.2)
2.Так как ширина полки таврового сечения может быть достаточно большой, например для балок, входящих в состав балочного монолитного перекрытия, то ширина полки балки b'f принимается с учетом следующих условий:
2.1. Ширина свеса полки в каждую сторону от ребра балки bсв = (b'f - b)/2 (на рисунке 326 не показана) должна быть не более 1/6 длины пролета рассчитываемого элемента, а также не более:
2.2. При наличии поперечных ребер (второстепенных балок при расчете главных балок или главных балок при расчете второстепенных балок, при этом ребро рассматриваемой балки считается продольным) или при h'f ≥ 0.1h расчетная ширина полки b'f принимается равной 1/2 расстояния между продольными ребрами в свету.
2.3. При отсутствии поперечных ребер или при расстоянии между поперечными ребрами большем, чем расстояния между продольными ребрами и при h'f < 0.1h расчетная ширина полки b'f = 6h'f.
2.4. При консольных свесах полки (при расчете отдельных балок таврового сечения, не входящих в состав разного рода перекрытий):
а) при h'f ≥ 0.1h расчетная ширина полки b'f = 6h'f;
б) при 0.05h ≤ h'f < 0.1h расчетная ширина полки b'f = 3h'f;
в) при h'f < 0.05h свесы полок в расчетах не учитываются.
2.5. При изменяющейся высоте свесов полки в расчетах допускается использовать среднее значение высоты h'f.
Все это, так сказать, теоретические, а потому не совсем понятные положения, давайте посмотрим, как их можно применить на практике.
Пример расчета на прочность балки таврового сечения
Планируется монолитное перекрытие в жилом помещении размерами 5х8 метров с 4 главными балками. Предварительно принятая высота основной плиты 8 см, предварительные размеры балок 10х15 см:
Рисунок 326.2
Примечание: На общей расчетной схеме (рис.326.2.а) размеры даны в миллиметрах, а размеры поперечного сечения балки (рис.326.2.б) даны в сантиметрах для упрощения дальнейших расчетов. Конструктивная арматура основной плиты для упрощения расчетов не учитывается.
1. Если и основная плита и балки будут бетонироваться одновременно, то высота основной плиты будет высотой полки h'f, а общая высота тавровой балки h = 8 + 15 = 23 см, а = 2.5 см, ho = 20.5 см. Для перекрытия будет использоваться бетон класса В20, с расчетным сопротивлением сжатию Rb = 11.5 МПа (117 кгс/см2) и арматура класса AIII (А400), имеющая расчетное сопротивление растяжению Rs = 355 МПа (3600 кгс/см2). В случае если бетонная смесь будет приготавливаться в домашних условиях (т.е. без должного контроля прочности образцов) и бетонирование будет выполняться не специалистами расчетное сопротивление бетона следует понизить. СНиПом СНиП 2.03.01-84 понижающий коэффициент, учитывающий качество выполнения работ, для подобных случаев не предусмотрен, да и тяжело предугадать, насколько сильно вышеуказанные причины могут повлиять на расчетное сопротивление бетона. Ориентировочно значение этого коэффициента может составлять от 0.5, если нет уверенности в своих силах, до 0.9, если уверенность в своих силах высокая. Дальнейший расчет будет производиться с использованием коэффициента качества работ γк = 0.9. Тогда расчетное значение сопротивления бетона сжатию составит:
Rb = 117·0.9 = 105.3 кг/см2
2. Пролет балок составляет 5 м, при этом bсв ≤ 500/6 = 83 см, первое условие соблюдается. Рассматриваемая балка входит в состав монолитного перекрытия, при этом высота плиты 8 см > 0.1h = 2.3 см, согласно п.2.2 расчетная ширина полки составит:
b'f = 152/2 = 76 см
3. Для определения высоты сжатой зоны сечения сначала необходимо определить максимальный изгибающий момент, действующий в рассматриваемом поперечном сечении тавровой балки. А для этого нужно знать нагрузки, действующие на перекрытие.
При расчете перекрытий жилых зданий в качестве расчетной временной нагрузки можно использовать следующее значение qвр = 400 кг/м2. Для балок с шагом 162 см расчетная временная нагрузка на погонный метр составит
qвр = 400·1.62 = 648 кг/м
Примечание: Более точное значение расчетной нагрузки следует определять по СНиП 2.01.07-85 "Нагрузки и воздействия", где приводятся значения нормативных нагрузок. Согласно указанного СНиП для плит перекрытий в квартирах жилых зданий нормативное значение распределенной нагрузки составляет 150 кг/м2. Затем это значение нужно умножить на коэффициент надежности по нагрузке, при таком значении нормативной нагрузки составляющий γн = 1.3 (1.4 по старым нормам). Таким образом расчетное значение временной нагрузки без учета стяжки, напольного покрытия и возможных других временных нагрузок составит
qсв = 150·1.3 = 195 кг/м2
Как показывает практика, если к определенной таким образом временной распределенной нагрузке прибавить временные нагрузки от выравнивающей стяжки, напольного покрытия и др., умноженные на соответствующие коэффициенты надежности по нагрузке, то суммарная временная нагрузка будет немного меньше указанных 400 кг/м2. Если до начала расчетов известна толщина будущей стяжки, вид напольного покрытия, расположение мебели и инженерного оборудования, то значение суммарной временной нагрузки можно рассчитать более точно. При этом значение расчетной временной нагрузки может снизиться на 30-70 кг/м2. Тем не менее дальнейший расчет будет выполняться по указанной выше временной нагрузке 400 кг/м2.
Примечание: Устройство каких-либо перегородок данным расчетом не предусматривается. Если по перекрытию планируется устройство перегородок, то следует предусмотреть отдельные балки под перегородки и рассчитать их с учетом возможных нагрузок. Исключение могут составлять легкие перегородки из ГКЛ, возле которых не будет устанавливаться мебель.
Постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.08·1.62 + 0.1·0.15)2500 = 361.5 кг/м. Коэффициент надежности по нагрузке для бетонных и железобетонных конструкций составляет γн = 1.1. Тогда расчетное значение постоянной нагрузки составит qпр = 361.5·1.1 = 397.65 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 397.65 +648 = 1045.65 кг/м
Тогда максимальный изгибающий момент для бесконсольной балки на двух шарнирных опорах:
Мmax = ql2/8 = 1045.65·52/8 = 3267.656 кг·м = 326765.6 кг·см
Почему это так, достаточно подробно рассказывается в другой статье.
4. Проверяем выполнение условия (326.1.2):
M = 326765.6 < Rbb'fh'f(ho - 0.5h'f) = 105.3·76·8(20.5 - 4) = 1056369.6
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 326765.6/(105.3·76·20.52) = 0.09716
6. am = 0.09716 < aR = 0.39/1.5 = 0.26, значит арматура в сжатой зоне не требуется, тогда требуемая площадь сечения арматуры в растянутой зоне составит:
Аs = 105.3·76·20.5(1 - √1 - 2·0.09716)/3600 = 4.67 см2
Диаметр арматуры можно подобрать по следующей таблице:
Таблица 2. Площади поперечных сечений и масса арматурных стержней.
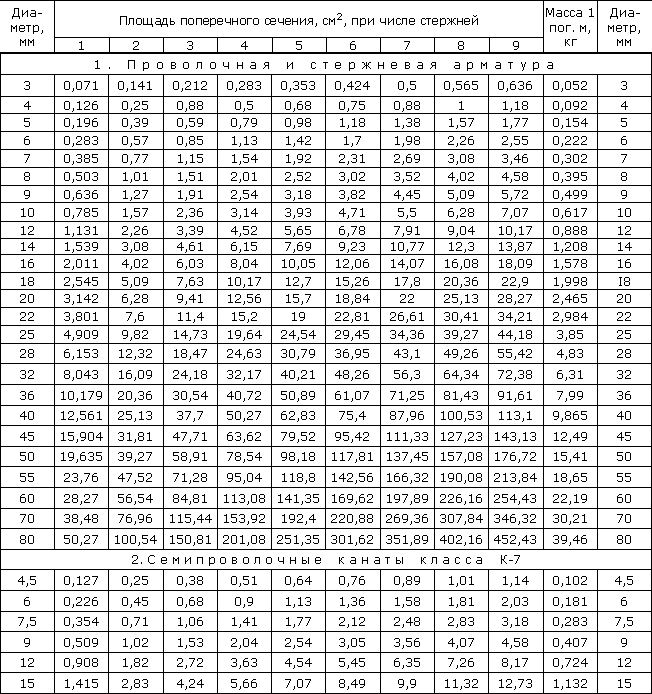
7. Для армирования балки можно использовать 2 стержня диаметром 18 мм, площадь сечения стержней составит 5.09 см2.
8. Проверяем соблюдение необходимой толщины защитного слоя бетона при выбранной арматуре. Толщина защитного слоя согласно п.5.5 СНиП 2.03.01-84 должна быть не менее диаметра арматуры и ≥ 15 мм. В нашем случае толщина защитного слоя бетона составит:
hз = а - d/2 = 25 - 18/2 = 16 мм
Условие не выполнено, поэтому для расчетов следует принять большее значение а. Например, при а = 27 мм ho = 20.3 см.
аm = 326765.6/(105.3·76·20.32) = 0.0991
Аs = 105.3·76·20.3(1 - √1 - 2·0.0991)/3600 = 4.71 см2
9. Расстояние в свету между стержнями арматуры составит 100 - 2а - d = 100 - 54 - 18 = 28 мм. Это означает, что для для бетонирования балки следует использовать бетонную смесь с максимальным размером зерен щебня 28 мм. Если предполагается использование крупного заполнителя больших размеров, то следует или увеличить ширину балки, или увеличить высоту балки, что позволит уменьшить диаметр используемой арматуры.
Примечание: если балки и плита будут бетонироваться отдельно, то тогда балки следует рассчитывать как элементы прямоугольного сечения с высотой, равной высоте балок.
Пример расчета балки таврового сечения с учетом прогиба
Выполненный выше расчет на прочность (расчет по первой группе предельных состояний) как правило для шарнирно опертых однопролетных балок недостаточен и требует дополнительного расчета по деформациям. Методик определения прогиба ж/б конструкций существует несколько. На мой взгляд проще всего определить приблизительное значение прогиба при расчете по допускаемым нагрузкам.
Расчет по допускаемым нагрузкам, предполагающий упругую работу материала и не предусматривающий пластические деформации в сжатой зоне бетона, дает следующие результаты:
При определенных выше параметрах высота сжатой зоны бетона составит:
y = √3M/2b'fRb = √3·326765.6/2·76·105.3 = 7.826 см
При этом требуемая высота сжатой зоны при расчете по деформациям определяется решением следующего кубического уравнения:
у3 = 3As(ho - y)2Es/b'fEb (321.2.4)
и при Еb = 270000 кгс/см2, Es = 2000000 кгс/см2, составит примерно уf = 6.53 см (ур = 5.234 см).
Тогда при Ip = b'f(2yp)3/12 = 76(2·5.234)3/12 = 7264.8 см4 примерный прогиб балки составит:
f = 0.83·5·10.456·5004/(384·270000·7264.8) = 3.6 см > fu = 500/250 = 2 см (согласно СНиП 2.01.07-85)
Это достаточно большой прогиб и для его уменьшения можно увеличить количество балок, но можно и увеличить высоту и ширину сечения принятого количества балок, тем более, если это необходимо сделать для использования бетонной смеси с крупным щебнем. Например, при увеличении высоты балки всего на 2 см - до 17 см и ширины балки до 11 см и при той же арматуре ho = 22.3 см:
уf = 7 см (yp = 6.174 см), Ip = 76(2·6.174)3/12 = 11924 см4, приблизительный прогиб
f = 0.83·5·10.456·5004/(384·270000·11924) = 2.194 см ≈ fu = 2 см.
Примечание: приведенная методика определения прогиба не является рекомендованной нормативными документами, к тому же для упрощения расчетов не учитывалось то, что немного увеличится нагрузка от собственного веса балки. Тем не менее такая методика позволяет достаточно быстро определить приблизительное значение прогиба и оценить его влияние на работу конструкции.
Пример расчета на прочность балки таврового сечения с учетом изменения высоты полки
Так как при расчетах плиты принята новая высота плиты h = 6 см, то это вносит ощутимые изменения в значение постоянной нагрузки и в параметры тавровой балки.
В этом случае при общей высоте балки h = 25 см постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.06·1.62 + 0.11·0.19)2500 = 295.25 кг/м. Тогда расчетное значение постоянной нагрузки составит qпр = 295.25·1.1 = 324.8 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 324.8 +648 = 972.8 кг/м
Мmax = ql2/8 = 972.8·52/8 = 3040 кг·м = 304000 кг·см
4. Проверяем выполнение условия (326.1.2):
M = 304000 < Rbb'fh'f(ho - 0.5h'f) = 105.3·76·6(22.3 - 3) = 926724.2
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 304000/(105.3·76·22.32) = 0.07638
Аs = 105.3·76·22.3(1 - √1 - 2·0.07638)/3600 = 3.943 см2
Как видим требуемая площадь сечения уменьшилась, но так как мы принимали сечение арматуры с учетом прогибов, то диаметр арматуры оставляем без изменения 2 стержня d = 18 мм.
При этом высота сжатой зоны бетона составит:
y = √3M/2b'fRb = √3·304000/2·76·105.3 = 7.55 см
Требуемая высота сжатой зоны при расчете по деформациям составит примерно уf = 7.07 см
Однако такая высота сжатой зоны означает, что нейтральная линия будет проходить не в полке а в ребре балки, и значение у также будет другим.
По более точной формуле значение моментов инерции полусечений составит:
Iв = b'fhf(y/2)2 +b'fhf3/12 + b(y - hf)((y - hf)/2)2 + b(y - hf)3/12 = Iн = As(ho - y)2Es/Eb (321.2.3.2)
тогда, подставив имеющиеся значения, получим:
76·6(у/2)2 + 76·63/12 + 11(у - 6)(y/2 - 3)2 + 11(y - 6)3/12 = 5.09(22.3 - y)22000000/270000;
114y2 + 1368 + 2.75(y - 6)3 + 0.917(y - 6)3 = 43.704(22.3 - y)2;
у ≈ 8.08 см
Так как требуемая высота сжатой зоны при расчете на прочность больше, чем высота сжатой зоны при расчете по деформациям (разница составит примерно 7.55-7.05 = 0.5 см), то при приближенном расчете (без учета области пластических деформаций) расчетное значение высоты полки составит 6 - 0.5 = 5.5 см, тогда
Ip = 76·5.5·3.792 + 76·5.53/12 + 3.667·2.083 = 6004.2 + 1053.71 +33 = 7090.9 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 3.43 см > fu = 2 см, а значит высоту балок желательно увеличить еще.
Например, при общей высоте h = 30 см
у ≈ 10.02 см
Ip = 76·5.5·4.762 + 76·5.53/12 + 3.667·4.023 = 9470.9 + 1053.71 + 238.2 = 10762.8 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 1.9 см < fu = 2 см
Если произвести расчет с учетом изменяющего модуля упругости бетона, то при Еb1 = 270000/(1 + 2.8) = 71052.6 кг/см2.
76·6(у/2)2 + 76·63/12 + 11(у - 6)(y/2 - 3)2 + 11(y - 6)3/12 = 5.09(27.3 - y)22000000/71052.6;
114y2 + 1368 + 2.75(y - 6)3 + 0.917(y - 6)3 = 166.0752(27.3 - y)2;
у ≈ 14.45 см и в этом случае высота сжатой области сечения принимается без изменений, тогда
Ip = 2·27410 = 54820 см4, тогда примерный прогиб балки составит:
f = 0.96·5·9.73·5004/(384·71052.6·54820) = 1.95 см < fu = 2 см
doctorlom.com
Балка таврового сечения железобетонная
Балки таврового сечения находят свое применение при строительстве автодорожных мостов. Они являются его опорной конструкцией, что предъявляет к их изготовлению высочайшие требования.
Общая информацияТехнические характеристикиНаши клиенты по данной продукции
Запрос прайс-листа
Общая информация
Широкое использование и применение железобетонных балок обусловлено потребностью в износостойком материале, который не подвластен воздействию огня и коррозии. В целом балки классифицируются по назначению, особенностям сечения и типу конструкции. В процессе строительства особое внимание уделяется как раз способу сечения, так как от этого показателя зависит прочность и устойчивость дальнейшей конструкции.
Форма сечения представляет собой разделение балок по способу монтажа и техническим особенностям материала. Зачастую выделяют четыре вида сечения: прямоугольные, которые применяются в обустройстве пролетов, с длиной в 12 метров; консольные; тавровые; а также T/L-образные. Несмотря на разнообразность видов и форм железобетонных балок, большую популярность при строительстве автодорожных мостов имеют именно балки железобетонные таврового сечения.
Тавровое сечение обеспечивает прочную конструкцию, которая выдерживает нагрузки на порядок выше, нежели консольные и прямоугольные балки. Несмотря на прочность и стойкость конструкции, весьма небольшой вес балки обеспечивает легкость при планировке, транспортировке и ее дальнейшей установке.
Рассматривая размеры ЖБ балок таврового сечения, нельзя выделить определенные габариты, так как широкое применение предусматривает разную форму материала. Наш завод ЖБИ осуществляет производство железобетонных балок таврового сечения в достаточно широкой номенклатуре.
Технические характеристики тавровых балок: размеры, вес
Особенность изготовления балок в современных условиях производства, предусматривает возможность создания изделий индивидуальных размеров. Конечно, основные габариты и форма не меняются, но подделать их под определенный разъем и размер вполне возможно. Длина одной балки у нас может колебаться от 12 м до 18 м. В области строительного проектирования с использованием балок таврового сечения, размеры высчитываются до разницы одного сантиметра, ее длинны и ширины.
Стоит отметить, что тавровое сечение значительно отличается от треугольного и консольного. В виду того, что сжатая зона поперечного сечения отличается от стандартных, необходимо правильно просчитывать размеры с учетом ребер материала. Также тавровое сечение предусматривает наличие арматуры, которая должна учитываться при распределении нагрузки и размещении балки.
| Наименование | Длина (мм) | Ширина (мм) | Высота (мм) | Масса (кг) |
| Б 1-12-3 И | 12000 | 1300 | 900 | 10900 |
| Б 1-12-3 сб | 12000 | 1300 | 900 | 10900 |
| Б 1-12-4 нб | 12000 | 1300 | 900 | 10850 |
| Б 1-12-4 св | 12000 | 1300 | 900 | 10850 |
| Б 1-12-4 св (КР) | 12000 | 1300 | 900 | 12425 |
| Б 2-12-3 сб | 12000 | 1300 | 900 | 10900 |
| Б 2-12-4 нб | 12000 | 1300 | 900 | 10850 |
| Б 3-12-3 сб | 12000 | 1300 | 900 | 10900 |
| Б 1-15-3 И | 15000 | 1300 | 900 | 13600 |
| Б 1-15-3 нб | 15000 | 1300 | 900 | 13600 |
| Б 1-15-3 сб | 15000 | 1300 | 900 | 13600 |
| Б 1-15-4 ис-315 | 15000 | 1300 | 900 | 13600 |
| Б 1-15-4 нб | 15000 | 1300 | 900 | 13600 |
| Б 2-15-3 сб | 15000 | 1300 | 900 | 13600 |
| Б 2-15-4 ис-315 | 15000 | 1300 | 900 | 13600 |
| Б 3-15-3 сб | 15000 | 1300 | 900 | 13600 |
| Б 1-18-3 И | 18000 | 1300 | 1050 | 17600 |
| Б 1-18-3 сб | 18000 | 1300 | 1050 | 17650 |
| Б 1-18-4 нб | 18000 | 1300 | 1050 | 17650 |
| Б 2-18-3 сб | 18000 | 1300 | 1050 | 17650 |
| Б 3-18-3 сб | 18000 | 1300 | 1050 | 17650 |
| Б 2-18-4 нб | 18000 | 1300 | 1050 | 17600 |
НАВЕРХ
Завод железобетонных изделий ООО «ПСК ПЕРСПЕКТИВА».
psk-energo.ru
Поиск Лекций
|
|
poisk-ru.ru
Расчет железобетонной балки таврового сечения
⇐ ПредыдущаяСтр 7 из 18Следующая ⇒Расчет производится аналогично балки прямоугольного сечения до пункта 2, здесь определяется значение расчетной высоты .
рис 3.3 Расчетное сечение
Затем производим определение значения внутреннего момента Mf, для того чтобы определить положение нейтральной оси и случай расчета, по формуле:
,(3.23)
где:Rb-расчетное сопротивление бетона осевому сжатию с учетом коэффициента , кН/см2;
-высота полки, см;
-ширина полки, см.
При сравнении Mf > M, то это первый случай расчета, нейтральная ось в полке.
Расчет производим как для прямоугольного сечения шириной , по формуле:
, (3.24)
Производим сравнение α < αR, уточняя армирование. По α определяем значение коэффициента η, следовательно, рабочая арматура рассчитывается, по формуле 3.16
Дальнейший расчет соблюдается, как для прямоугольного сечения.
Графическая часть выполняется таким же образом.
Указания по выполнению расчетно - графической
работы по разделу:
«Соединение элементов стальных ферм»
Расчет узла фермы
Расчет производится по 2-м основным направлениям:
1)подбор уголков для ветвей фермы;
2)расчет сварных соединений в узлах фермы.
1.Подбор уголков для формирования ветвей фермы
Подбор производится по max усилиям определенных в стержнях фермы по диаграмме Максвелла – Кремоны. За основание расчета берется длина панели, которая равна ширине плиты покрытия l0. Коэффициент условия работы пояса .
Для расчета используют формулу:
,(4.1)
где:φ-коэффициент продольного изгиба;
А–площадь поперечного сечения ветви фермы, см2;
N–наибольшее усилие в стержнях, принятое по диаграмме (по заданию), кН;
Ry –расчетное сопротивление стали по пределу текучести (СНиП II-23-81* Стальные конструкции, табл.51), кН/см2;
γc–коэффициент условий работы элемента.
Данная формула используется для определения площади поперечного сечения будущих использованных в сечении уголков, получаем формулу:
,(4.2)
где: φ–коэффициент продольного изгиба, задается в приделах (0,6 - 0,8).
После подбора площади уточняют количество уголков использованных в ветвях фермы (наиболее часто распространенное количество – два уголка).
Для получения площади одного уголка площадь всех А, см2 делим на два (количество уголков). По полученной площади по сортаменту прокатных профилей подбираем уголок, выписывая номер уголка, радиусы инерции и моменты инерции в плоскостях х и у (ix,y; Ix,y ).
Уточняем площадь А, см2 для двух подобранных уголков. Рассчитываем гибкости в плоскостях х и у , через радиусы инерции, по формулам:
,(4.3)
,(4.4)
Соответственно каждой гибкости определяем коэффициент продольного изгиба по таблице. Наибольшее значение принимаем к расчету, который производится, по формуле:
,(4.5)
Если условие выполняется, то подобранные уголки удовлетворяют условиям эксплуатации. Если условие не выполняется, то необходимо пересмотреть уголки или расстояние между узлами фермы (изменить l0 ).
2.Расчет сварных соединений узла фермы
Расчет заключается в определении длин сварных швов у фасонки узла. Уточняем нагрузки у пера и обушка, по формулам:
,(4.6)
,(4.7)
где:α-коэффициент, учитывающий возможность приваривания уголка к пластине (если уголок равнополочный 0,7).
Длина шва рассчитывается из условия работы шва на срез по границе сплавления или по шву.
Суммарно длина шва обушка из условия работы на срез по металлу шва определяется, по формуле:
,(4.8)
где:βf=0,7 при ручной сварки;
kf-высота шва;
kf=1,2 . tmin;
Rwf–расчетное сопротивление углового сварного шва при работе на срез (зависит от типа электрода, наиболее распространенная марка Э-42 СНиП II-23-81* Стальные конструкции, табл.56), кН/см2;
γwf=1–коэффициент условий работы шва;
γc=0,9
Аналогично производится расчет по границе сплавления, для этого используют формулу:
,(4.9)
где:βz=1
γwz=1
Rwz-расчетное сопротивление углового шва при расчете по границе сплавления (определяется, как 0,45∙Run, если Run-нормативное значение временного сопротивления, определяемого по марки стали СНиП II-23-81* Стальные конструкции, табл. 51), кН/см2
Суммарная длина швов у пера, из условия работы на срез по границе сплавления определяется, по формуле:
,(4.10)
где:kf =tуг - (1…2)мм.
Расчет по металлу шва производится, по формуле:
,(4.11)
Графическая часть.
Рисунок узла фермы выполняется по ходу решения задачи карандашом с указанием на рисунке расстановки сил и используемых уголков.
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru
Расчет железобетонной балки таврового сечения
Расчет железобетонной балки таврового сечения. Расчет железобетонной балки таврового сечения от расчета балки прямоугольного сечения отличается тем, что следует учитывать высоту сжатой зоны поперечного сечения. Так как геометрические размеры тавровых сечений бывают разными, то сжатая зона бетона может быть или только в полке тавра или и в полке и частично в ребре. Кроме того следует учитывать наличие или отсутствие арматуры в сжатой зоне сечения. Далее будут рассматриваться примеры расчетов для тавровых сечений, у которых отсутствует арматура в сжатой зоне для упрощения изложения и с учетом того, что такие случаи в практике малоэтажного строительства встречаются намного чаще Теоретические основы расчета Согласно СНиП 2.03.01-84 и СП 52-101-2003 расчет тавровых поперечных сечений без арматуры в сжатой зоне рекомендуется выполнять с использованием следующих положений: 1. а) Если нейтральная плоскость (граница между сжимаемой и растягиваемой зонами сечения) проходит в полке (рисунок 326.1.а), т.е. соблюдаются условия:RsAs M ≤ Rbb'fh'f(ho - 0.5h'f) (326.1.2) и ξ = у/ho то расчет производится, как для балки прямоугольного сечения с шириной b'f. Подробности расчета по такому алгоритму подробно расписаны в статье "Расчет железобетонной плиты перекрытия". Здесь же приведу только основные формулы: ξR - предельно допустимое значение относительной высоты сжатой зоны бетона, определяемое по следующей формуле: (220.6.2) где Rs - расчетное сопротивление арматуры в МПа. Также предельное значение относительной высоты сжатой зоны бетона можно определить по таблице: Таблица 220.1. Граничные значения относительной высоты сжатой зоны бетонаПримечание: При выполнении расчетов не профессиональными проектировщиками, ограничивающимися только расчетами по первой группе предельных состояний, я рекомендую занижать предельное значение относительной высоты сжатой зоны ξR (и значение аR) в 1.3-1.5 раза. В связи с этим возможный вариант расчета, когда y > ξRho, далее не рассматривается. При определении сечения арматуры сначала определяется коэффициент am: (220.6.6) при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.1. При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле: (220.6.7) В формулах (220.6.6) и (220.6.7) значения b заменяются на b'f.
Рисунок 326.1 1. б) Если нейтральная плоскость проходит в ребре балки (рисунок 326.1.б), то расчет выполняется, исходя из следующего условия: M < Rbbу (h0 - 0,5у) + Rbh'f(b'f - b)(h0 - 0.5h'f) (326.2) где (b'f - b)h'f = Aov - площадь сечения свесов полки. При этом высота сжатой зоны у определяется, исходя из следующих формул: RsAs = Rbby + Rbh'f(b'f - b) (326.3.1) y = (RsAs - RbAov)/Rbb (326.3.2) при этом высота сжатой зоны принимается у ≤ ξRho. При определении сечения арматуры сначала определяется коэффициент am: (326.4.1) при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.1 (см. выше). При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле: (326.4.2) 2.Так как ширина полки таврового сечения может быть достаточно большой, например для балок, входящих в состав балочного монолитного перекрытия, то ширина полки балки b'f принимается с учетом следующих условий: 2.1. Ширина свеса полки в каждую сторону от ребра балки bсв = (b'f - b)/2 (на рисунке 326 не показана) должна быть не более 1/6 длины пролета рассчитываемого элемента, а также не более: 2.2. При наличии поперечных ребер (второстепенных балок при расчете главных балок или главных балок при расчете второстепенных балок, при этом ребро рассматриваемой балки считается продо
filesclub.net
Железобетонные конструкции (II часть)
Добавлено: 09 Апр 2015, Armin проф. В А. Бушков Железобетонные конструкции (II часть) СТРОЙИЗДАТ НАРКОМСТРОЯ 1941 ___________________________________________________________________________ За сканы огромное спасибо Timonicheff.Плоды темы "Ваши сканы, наша обработка и перевод в DJVU". http://forum.dwg.ru/showthread.php?t=38054
Оглавление
Предисловие 8 РАЗДЕЛ I ИЗГИБ И СКАЛЫВАНИЕ ПРИ ИЗГИБЕ 10 Глава I. Конструкции, работающие на изгиб и скалывание при изгибе. Плоские покрытия и перекрытия 10 Глава II. Статический расчет изгибаемых элементов железобетонных конструкций 23 1. Предварительные сведения 23 2. Расчет балочных плит 25 3. Расчет плит, опертых по контуру (плиты с перекрестной арматурой) 28 4. Расчет балок 40 Глава III. Работа балки на изгиб. Три стадии напряженности 48 Глава IV. Расчет прочности балок на изгиб 53 А. Прямоугольная балка или плита с одиночной арматурой 53 1. Формулы для определения Мр и плеча пары внутренних сил z 53 2. Опытная проверка расчетной формулы Мр 56 3. Предельные значения процента армирования балок 60 4. Оптимальный процент армирования прямоугольных балок и плит 62 5. Таблицы для расчета плит и балок прямоугольного сечения с одиночной арматурой 64 6. Примеры расчета прямоугольных сечений балок с одиночной арматурой 67 Б. Прямоугольная балка или плита с двойной арматурой 70 1. Формулы для определения Мр 70 2. Армирование при различном соотношении площадей сжатой и растянутой арматуры. Армирование при условии min (Fa+Fa’) 75 3. Примеры расчета плит и балок с двойной арматурой 79 В. Балка таврового сечения 83 1. Работа тавровой балки на изгиб 83 2. Наименьший процент армирования растянутой зоны балок таврового сечения 87 3. Расчет 0алок таврового сечения на отрицательный момент 88 4. Расчет балок таврового сечения на положительный момент 89 5. Выбор высоты балок таврового сечения 93 6. Примеры расчета балок таврового сечения 98 Глава V. Расчет и конструирование арматуры плит перекрытий (балочные плиты и плиты, опертые по контуру) 99 1. Конструктивные указания по проектированию балочных плит и плит, опертых по контуру 99 2. Пример расчета и конструирования балочных плит ребристого перекрытия 105 3. Пример расчета и конструирования плиты кессонного перекрытия 110 Глава VI. Расчет изгибаемых элементов, на поперечную силу 116 1. Работа балок при поперечном срезе по данным опытов 116 2. Скалывающие напряжения и главные напряжения в балке 125 3. Расчетные эпюры огл = т вдоль балки 131 4. Оценка по эпюре огл = о сопротивляемости балки главным растягивающим напряжениям. Распределение эпюры на части с передачей их на продольную арматуру, хомуты и косые стержни 136 5. Расчет и конструирование хомутов 144 6. Расчет и конструирование отогнутой арматуры 148 7. Эпюра арматуры. Прочность балки по нормальным и косым сечениям 154 Глава VII. Расчет и конструирование балок по изгибу и поперечному срезу 159 1. Конструктивные указания по проектированию балок 159 2. Пример расчета и конструирования однопролетных свободно лежа¬щих балок с равномерно распределенной нагрузкой 161 3. Пример расчета и конструирования однопролетных свободно лежащих балок под действием сосредоточенных сил 166 4. Пример расчета и конструирования неразрезных балок ребристого перекрытия 169 5. Применение вутов в неразрезных балках ребристого перекрытия 190 Глава VIII. Консоли, их расчет и конструирование 197 1. Примеры применения консолей в строительстве 197 2. Расчет и конструирование консолей с большим вылетом 200 3. Расчет и конструирование коротких консолей 202 Глава IX. Расчет изгибаемых элементов, к которым предъявляются требования непроницаемости бетона 209 1. Изгибаемые элементы с обыкновенной арматурой и с арматурой, имеющей предварительное натяжение 209 А. Расчет на изгиб бетонных неармированных балок 214 2. Расчет бетонных неармированных балок на изгиб по ТУ и Н проектирования бетонных конструкций (ОСТ 90040-39) 214 3. Расчет бетонных неармированных балок на изгиб по стадии напряженности IIa 215 Б. Расчет на изгиб железобетонных балок с обыкновенной арматурой 220 4. Расчет железобетонных балок на изгиб по стадии напряженности I 220 5. Расчет на изгиб железобетонных балок прямоугольного сечения с одиночной или с двойной арматурой по стадии напряженности IIa 222 6. Расчет на изгиб железобетонных балок прямоугольного сечения по стадии напряженности IIb 227 7. Примеры расчета и сопоставление различных приемов расчета 232 В. Расчет на изгиб балок с предварительно напряженной арматурой 238 8. Определение Mm для балок прямоугольного сечения с двойной арматурой, имеющей предварительное натяжение 238 9. Определение Mm для балок прямоугольного сечения с одиночной или двойной арматурой, часть стержней которой имеет предвари¬тельное натяжение 242 10. Потеря арматурой первоначального (монтажного) напряжения 244 11. Сравнение результатов расчета по выведенным формулам с опытными данными для железобетонных балок прямоугольного сечения с одиночной арматурой, имеющей предварительное натяжение 245 12. Графики и таблицы для расчета Mm. Примеры расчёта на изгиб балок с предварительно напряженной арматурой 248 13. Расчет на положительный момент балок таврового сечения с арматурой, имеющей предварительное натяжение 258 РАЗДЕЛ II ОСЕВОЕ И ВНЕЦЕНТРЕННОЕ СЖАТИЕ 263 Глава X. Элементы железобетонных конструкций, работающие на осевое и внецентренное сжатие (колонны и стойки, рамные и арочные конструкции) 263 1. Общие сведения 263 2. Конструкции, работающие на осевое и внецентренное сжатие 267 Глава XI. Осевое сжатие 272 А. Колонны с продольной арматурой и обык¬новенными хомутами 272 1. Расчет коротких колонн с продольной арматурой и обыкновенными хомутами 272 2. Конструктивные указания по проектированию на осевое сжатие колонн с продольной арматурой и обыкновенными хомутами 274 3. Продольный изгиб и его учет в расчетах прочности колонн 276 4. Примеры расчета колонн на осевое сжатие с продольной арматурой и обыкновенными хомутами 283 Б. Колонны со спиральной арматурой 285 5. Расчетные формулы и их обоснование 285 6. Конструктивные указания по проектированию «бетона в обойме» 291 7. Примеры расчета и конструирования колонн со спиральной арматурой («бетона в обойме») 294 Глава XII. Внецентренное сжатие колонн и стоек прямоуголь¬ного сечения с продольной арматурой и обыкно¬венными хомутами 297 1. Общие предпосылки к расчету внецентренно сжатых сечений. Принятые обозначения 297 2. Расчетные формулы для первого случая внецентренного сжатия 299 3. Расчетные формулы для второго случая внецентренного сжатия 306 4. Указания по конструированию и расчету внецентренно сжатых элементов 316 5. Учет гибкости колонн и стоек при расчете их на внецентренное сжатие 323 6. Примеры подбора сечений внецентренно сжатых элементов 328 7. Расчет на внецентренное сжатие элементов таврового сечения 347 8. Расчет на внецентренное сжатие при соблюдении требования непроницаемости бетона 353 РАЗДЕЛ III ОСЕВОЕ И ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ 358 Глава XIII. Элементы конструкций, работающие на осевое и внецентренное растяжение 358 Глава XIV. Осевое растяжение 361 1. Расчет прочности при осевом растяжении 361 2. Расчет, обеспечивающий требование непроницаемости бетона 362 3. Мероприятия, предотвращающие образование волосных трещин в бетоне растянутых элементов конструкции 364 Глава XV. Внецентренное растяжение 367 1. Первый случай внецентренного растяжения 367 2. Второй случай внецентренного растяжения 368 3. Примеры расчета сечений на внецентренное растяжение 371 4. Расчет на внецентренное растяжение при соблюдении требования непроницаемости бетона 374 РАЗДЕЛ IV КРУЧЕНИЕ В ЖЕЛЕЗОБЕТОНЕ 381 Глава XVI. Опыты и расчеты 381 1. Возникновение крутящих моментов в элементах конструкции и учет их в расчетах 381 2. Кручение бетонных круглых цилиндрических образцов. Определение огл = ткр. Опытные данные 385 3. Кручение бетонных элементов прямоугольного сечения. Определение огл = ткр 390 4. Армирование железобетонных элементов при кручении. Расчетные формулы. Пример расчета 394 5. Опытные данные при кручении армированных образцов 399 6. Совместное действие кручения и изгиба 403 Приложения 406 Приложение I. Таблицы для статического расчета железо¬бетонных конструкций 406 А. Таблица для расчета на изгиб плит, опертых по контуру, при сплошной равномерно распределенной нагрузке q 406 Б. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной р 408 В. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при сосредоточенной нагрузке: постоянной G и временной Р 412 Г. Таблица пролетных и опорных моментов и поперечных сил в опор¬ных сечениях неразрезных балок с равными пролетами 420 Д. Таблица опорных моментов для неразрезных балок с равными пролетами и постоянного сечения при любых нагрузках, симметричных по отношению к пролету. Концы балок могут быть свободно положены на опоры (схема I) или жестко заделаны в опорах (схема II) 430 Е. Таблица грузовых коэфициентов s балок с симметричной нагрузкой 433 Ж. Таблица моментов, поперечных сил и эквивалентных по моменту нагрузок для свободно лежащих балок 434 З. Таблица моментов в равнопролетной балке на упруго вращающихся опорах 435 Приложение 2. Таблицы и графики для расчета элементов железобетонных конструкций. 442 Iа. Таблица круглого железа 442 Iб. Таблица площадей арматуры в 1 пог. м плиты при различном расстоянии между стержнями 443 II. Таблица для расчета на изгиб плит и балок прямоугольного сечения с одиночной арматурой 444 III. Таблица для подбора прямоугольных сечений с одиночной арматурой 446 IV. График для расчета прямоугольных сечений на изгиб 447 V. Таблица для подбора сечений на изгиб с одиночной или двойной арматурой и на внецентренное сжатие и растяжение 448 VI. а, б, в, г, д. Графики расчета Мт для балок прямоугольного сечения с одиночной арматурой 450 VII. Таблица для подбора внецентренно сжатых прямоугольных се¬чений с двойной симметричной арматурой 455 VIII. График значении n1 Np/Rubh в зависимости от с0 = e0/h и о1 = a1’ = omFa/Rubh при внецентренном сжатии прямоугольных сечении с двойной симметричной арматурой при б1 = 0,08 458 IX. График для расчета внецентренно сжатых элементов прямоугольного сечения (б1 = б1’ = 0,08) 459 X. а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой 460 XI. График для определения моментов инерции тавровых сечений 462 XII. График для определения коэффициента m при расчете внецентренно сжатых сечений с учетом гибкости элемента 463 X.IIа. Таблица для расчета на изгиб балок прямоугольного сечения с предварительно напряженной арматурой. Марка бетона 250 кг/см2 464 XIIIб. То же. Марка бетона 300 кг/см2 465 ХIIIв. То же. Марка бетона 350 кг/см2 466 Приложение 3. Принятые обозначения 467 Приложение 4. Свод формул и правил расчета и конструирования железобетонных элементов 471dwg.ru
Расчет железобетонной балки таврового сечения
Расчет железобетонной балки таврового сечения.
Расчет железобетонной балки таврового сечения от расчета балки прямоугольного сечения отличается тем, что следует учитывать высоту сжатой зоны поперечного сечения. Так как геометрические размеры тавровых сечений бывают разными, то сжатая зона бетона может быть или только в полке тавра или и в полке и частично в ребре. Кроме того следует учитывать наличие или отсутствие арматуры в сжатой зоне сечения. Далее будут рассматриваться примеры расчетов для тавровых сечений, у которых отсутствует арматура в сжатой зоне для упрощения изложения и с учетом того, что такие случаи в практике малоэтажного строительства встречаются намного чаще
Теоретические основы расчета
Согласно СНиП 2.03.01-84 и СП 52-101-2003 расчет тавровых поперечных сечений без арматуры в сжатой зоне рекомендуется выполнять с использованием следующих положений:
1. а) Если нейтральная плоскость (граница между сжимаемой и растягиваемой зонами сечения) проходит в полке (рисунок 326.1.а), т.е. соблюдаются условия:
RsAs < Rbb'fh'f (326.1.1)
M ≤ Rbb'fh'f(ho - 0.5h'f) (326.1.2)
и
ξ = у/ho < ξR (220.6.1)
то расчет производится, как для балки прямоугольного сечения с шириной b'f. Подробности расчета по такому алгоритму подробно расписаны в статье "Расчет железобетонной плиты перекрытия". Здесь же приведу только основные формулы:
ξR - предельно допустимое значение относительной высоты сжатой зоны бетона, определяемое по следующей формуле:
(220.6.2)
где Rs - расчетное сопротивление арматуры в МПа. Также предельное значение относительной высоты сжатой зоны бетона можно определить по таблице:
Таблица 220.1. Граничные значения относительной высоты сжатой зоны бетона
Примечание: При выполнении расчетов не профессиональными проектировщиками, ограничивающимися только расчетами по первой группе предельных состояний, я рекомендую занижать предельное значение относительной высоты сжатой зоны ξR (и значение аR) в 1.3-1.5 раза. В связи с этим возможный вариант расчета, когда y > ξRho, далее не рассматривается.
При определении сечения арматуры сначала определяется коэффициент am:
(220.6.6)
при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.1.
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
(220.6.7)
В формулах (220.6.6) и (220.6.7) значения b заменяются на b'f.
Рисунок 326.1
1. б) Если нейтральная плоскость проходит в ребре балки (рисунок 326.1.б), то расчет выполняется, исходя из следующего условия:
M < Rbbу (h0 - 0,5у) + Rbh'f(b'f - b)(h0 - 0.5h'f) (326.2)
где (b'f - b)h'f = Aov - площадь сечения свесов полки.
При этом высота сжатой зоны у определяется, исходя из следующих формул:
RsAs = Rbby + Rbh'f(b'f - b) (326.3.1)
y = (RsAs - RbAov)/Rbb (326.3.2)
при этом высота сжатой зоны принимается у ≤ ξRho.
При определении сечения арматуры сначала определяется коэффициент am:
(326.4.1)
при аm < aR арматура в сжатой зоне не требуется, значение аR определяется по таблице 220.1 (см. выше).
При отсутствии арматуры в сжатой зоне сечение арматуры определяется по следующей формуле:
(326.4.2)
2.Так как ширина полки таврового сечения может быть достаточно большой, например для балок, входящих в состав балочного монолитного перекрытия, то ширина полки балки b'f принимается с учетом следующих условий:
2.1. Ширина свеса полки в каждую сторону от ребра балки bсв = (b'f - b)/2 (на рисунке 326 не показана) должна быть не более 1/6 длины пролета рассчитываемого элемента, а также не более:
2.2. При наличии поперечных ребер (второстепенных балок при расчете главных балок или главных балок при расчете второстепенных балок, при этом ребро рассматриваемой балки считается продольным) или при h'f ≥ 0.1h расчетная ширина полки b'f принимается равной 1/2 расстояния между продольными ребрами в свету.
2.3. При отсутствии поперечных ребер или при расстоянии между поперечными ребрами большем, чем расстояния между продольными ребрами и при h'f < 0.1h расчетная ширина полки b'f = 6h'f.
2.4. При консольных свесах полки (при расчете отдельных балок таврового сечения, не входящих в состав разного рода перекрытий):
а) при h'f ≥ 0.1h расчетная ширина полки b'f = 6h'f;
б) при 0.05h ≤ h'f < 0.1h расчетная ширина полки b'f = 3h'f;
в) при h'f < 0.05h свесы полок в расчетах не учитываются.
2.5. При изменяющейся высоте свесов полки в расчетах допускается использовать среднее значение высоты h'f.
Все это, так сказать, теоретические, а потому не совсем понятные положения, давайте посмотрим, как их можно применить на практике.
Пример расчета на прочность балки таврового сечения
Планируется монолитное перекрытие в жилом помещении размерами 5х8 метров с 4 главными балками. Предварительно принятая высота основной плиты 8 см, предварительные размеры балок 10х15 см:
Рисунок 326.2
Примечание: На общей расчетной схеме (рис.326.2.а) размеры даны в миллиметрах, а размеры поперечного сечения балки (рис.326.2.б) даны в сантиметрах для упрощения дальнейших расчетов. Конструктивная арматура основной плиты для упрощения расчетов не учитывается.
1. Если и основная плита и балки будут бетонироваться одновременно, то высота основной плиты будет высотой полки h'f, а общая высота тавровой балки h = 8 + 15 = 23 см, а = 2.5 см, ho = 20.5 см. Для перекрытия будет использоваться бетон класса В20, с расчетным сопротивлением сжатию Rb = 11.5 МПа (117 кгс/см2) и арматура класса AIII (А400), имеющая расчетное сопротивление растяжению Rs = 355 МПа (3600 кгс/см2). В случае если бетонная смесь будет приготавливаться в домашних условиях (т.е. без должного контроля прочности образцов) и бетонирование будет выполняться не специалистами расчетное сопротивление бетона следует понизить. СНиПом СНиП 2.03.01-84 понижающий коэффициент, учитывающий качество выполнения работ, для подобных случаев не предусмотрен, да и тяжело предугадать, насколько сильно вышеуказанные причины могут повлиять на расчетное сопротивление бетона. Ориентировочно значение этого коэффициента может составлять от 0.5, если нет уверенности в своих силах, до 0.9, если уверенность в своих силах высокая. Дальнейший расчет будет производиться с использованием коэффициента качества работ γк = 0.9. Тогда расчетное значение сопротивления бетона сжатию составит:
Rb = 117·0.9 = 105.3 кг/см2
2. Пролет балок составляет 5 м, при этом bсв ≤ 500/6 = 83 см, первое условие соблюдается. Рассматриваемая балка входит в состав монолитного перекрытия, при этом высота плиты 8 см > 0.1h = 2.3 см, согласно п.2.2 расчетная ширина полки составит:
b'f = 152/2 = 76 см
3. Для определения высоты сжатой зоны сечения сначала необходимо определить максимальный изгибающий момент, действующий в рассматриваемом поперечном сечении тавровой балки. А для этого нужно знать нагрузки, действующие на перекрытие.
При расчете перекрытий жилых зданий в качестве расчетной временной нагрузки можно использовать следующее значение qвр = 400 кг/м2. Для балок с шагом 162 см расчетная временная нагрузка на погонный метр составит
qвр = 400·1.62 = 648 кг/м
Примечание: Более точное значение расчетной нагрузки следует определять по СНиП 2.01.07-85 "Нагрузки и воздействия", где приводятся значения нормативных нагрузок. Согласно указанного СНиП для плит перекрытий в квартирах жилых зданий нормативное значение распределенной нагрузки составляет 150 кг/м2. Затем это значение нужно умножить на коэффициент надежности по нагрузке, при таком значении нормативной нагрузки составляющий γн = 1.3 (1.4 по старым нормам). Таким образом расчетное значение временной нагрузки без учета стяжки, напольного покрытия и возможных других временных нагрузок составит
qсв = 150·1.3 = 195 кг/м2
Как показывает практика, если к определенной таким образом временной распределенной нагрузке прибавить временные нагрузки от выравнивающей стяжки, напольного покрытия и др., умноженные на соответствующие коэффициенты надежности по нагрузке, то суммарная временная нагрузка будет немного меньше указанных 400 кг/м2. Если до начала расчетов известна толщина будущей стяжки, вид напольного покрытия, расположение мебели и инженерного оборудования, то значение суммарной временной нагрузки можно рассчитать более точно. При этом значение расчетной временной нагрузки может снизиться на 30-70 кг/м2. Тем не менее дальнейший расчет будет выполняться по указанной выше временной нагрузке 400 кг/м2.
Примечание: Устройство каких-либо перегородок данным расчетом не предусматривается. Если по перекрытию планируется устройство перегородок, то следует предусмотреть отдельные балки под перегородки и рассчитать их с учетом возможных нагрузок. Исключение могут составлять легкие перегородки из ГКЛ, возле которых не будет устанавливаться мебель.
Постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.08·1.62 + 0.1·0.15)2500 = 361.5 кг/м. Коэффициент надежности по нагрузке для бетонных и железобетонных конструкций составляет γн= 1.1. Тогда расчетное значение постоянной нагрузки составит qпр = 361.5·1.1 = 397.65 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 397.65 +648 = 1045.65 кг/м
Тогда максимальный изгибающий момент для бесконсольной балки на двух шарнирных опорах:
Мmax = ql2/8 = 1045.65·52/8 = 3267.656 кг·м = 326765.6 кг·см
Почему это так, достаточно подробно рассказывается в другой статье.
4. Проверяем выполнение условия (326.1.2):
M = 326765.6 < Rbb'fh'f(ho - 0.5h'f) = 105.3·76·8(20.5 - 4) = 1056369.6
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 326765.6/(105.3·76·20.52) = 0.09716
6. am = 0.09716 < aR = 0.39/1.5 = 0.26, значит арматура в сжатой зоне не требуется, тогда требуемая площадь сечения арматуры в сжатой зоне составит:
Аs = 105.3·76·20.5(1 - √1 - 2·0.09716)/3600 = 4.67 см2
Диаметр арматуры можно подобрать по следующей таблице:
Таблица 2. Площади поперечных сечений и масса арматурных стержней.
7. Для армирования балки можно использовать 2 стержня диаметром 18 мм, площадь сечения стержней составит 5.09 см2.
8. Проверяем соблюдение необходимой толщины защитного слоя бетона при выбранной арматуре. Толщина защитного слоя согласно п.5.5 СНиП 2.03.01-84 должна быть не менее диаметра арматуры и ≥ 15 мм. В нашем случае толщина защитного слоя бетона составит:
hз = а - d/2 = 25 - 18/2 = 16 мм
Условие не выполнено, поэтому для расчетов следует принять большее значение а. Например, при а = 27 мм ho = 20.3 см.
аm = 326765.6/(105.3·76·20.32) = 0.0991
Аs = 105.3·76·20.3(1 - √1 - 2·0.0991)/3600 = 4.71 см2
9. Расстояние в свету между стержнями арматуры составит 100 - 2а - d = 100 - 54 - 18 = 28 мм. Это означает, что для для бетонирования балки следует использовать бетонную смесь с максимальным размером зерен щебня 28 мм. Если предполагается использование крупного заполнителя больших размеров, то следует или увеличить ширину балки, или увеличить высоту балки, что позволит уменьшить диаметр используемой арматуры.
Примечание: если балки и плита будут бетонироваться отдельно, то тогда балки следует рассчитывать как элементы прямоугольного сечения с высотой, равной высоте балок.
Пример расчета балки таврового сечения с учетом прогиба
Выполненный выше расчет на прочность (расчет по первой группе предельных состояний) как правило для шарнирно опертых однопролетных балок недостаточен и требует дополнительного расчета по деформациям. Методик определения прогиба ж/б конструкций существует несколько. На мой взгляд проще всего определить приблизительное значение прогиба при расчете по допускаемым нагрузкам.
Расчет по допускаемым нагрузкам, предполагающий упругую работу материала и не предусматривающий пластические деформации в сжатой зоне бетона, дает следующие результаты:
При определенных выше параметрах высота сжатой зоны бетона составит:
y = √3M/2b'fRb = √3·326765.6/2·76·105.3 = 7.826 см
При этом требуемая высота сжатой зоны при расчете по деформациям определяется решением следующего кубического уравнения:
у3 = 3As(ho - y)2Es/b'fEb (321.2.4)
и при HYPERLINK "http://doctorlom.com/item171.html" Еb = 270000 кгс/см2, Es = 2000000 кгс/см2, составит примерно уf = 6.53 см (ур = 5.234 см).
Тогда при Ip = b'f(2yp)3/12 = 76(2·5.234)3/12 = 7264.8 см4 примерный прогиб балки составит:
f = 0.83·5·10.456·5004/(384·270000·7264.8) = 3.6 см > fu = 500/250 = 2 см (согласно СНиП 2.01.07-85)
Это достаточно большой прогиб и для его уменьшения можно увеличить количество балок, но можно и увеличить высоту и ширину сечения принятого количества балок, тем более, если это необходимо сделать для использования бетонной смеси с крупным щебнем. Например, при увеличении высоты балки всего на 2 см - до 17 см и ширины балки до 11 см и при той же арматуре ho = 22.3 см:
уf = 7 см (yp = 6.174 см), Ip = 76(2·6.174)3/12 = 11924 см4, приблизительный прогиб
f = 0.83·5·10.456·5004/(384·270000·11924) = 2.194 см ≈ fu = 2 см.
Примечание: приведенная методика определения прогиба не является рекомендованной нормативными документами, к тому же для упрощения расчетов не учитывалось то, что немного увеличится нагрузка от собственного веса балки. Тем не менее такая методика позволяет достаточно быстро определить приблизительное значение прогиба и оценить его влияние на работу конструкции.
Пример расчета на прочность балки таврового сечения с учетом изменения высоты полки
Так как при расчетах плиты принята новая высота плиты h = 6 см, то это вносит ощутимые изменения в значение постоянной нагрузки и в параметры тавровой балки.
В этом случае при общей высоте балки h = 25 см постоянная нагрузка от собственного веса монолитного перекрытия на одну балку будет составлять qп = (0.06·1.62 + 0.11·0.19)2500 = 295.25 кг/м. Тогда расчетное значение постоянной нагрузки составит qпр = 295.25·1.1 = 324.8 кг/м. Таким образом суммарная распределенная нагрузка на балку составит:
qр = qп + qв = 324.8 +648 = 972.8 кг/м
Мmax = ql2/8 = 972.8·52/8 = 3040 кг·м = 304000 кг·см
4. Проверяем выполнение условия (326.1.2):
M = 304000 < Rbb'fh'f(ho - 0.5h'f) = 105.3·76·6(22.3 - 3) = 926724.2
5. Условие выполняется, расчет сечения арматуры в сжатой зоне можно производить по формулам (220.6.6) и (220.6.7), тогда:
аm = 304000/(105.3·76·22.32) = 0.07638
Аs = 105.3·76·22.3(1 - √1 - 2·0.07638)/3600 = 3.943 см2
Как видим требуемая площадь сечения уменьшилась, но так как мы принимали сечение арматуры с учетом прогибов, то диаметр арматуры оставляем без изменения 2 стержня d = 18 мм.
При этом высота сжатой зоны бетона составит:
y = √3M/2b'fRb = √3·304000/2·76·105.3 = 7.55 см
Требуемая высота сжатой зоны при расчете по деформациям составит примерно уf = 7.07 см
Однако такая высота сжатой зоны означает, что нейтральная линия будет проходить не в полке а в ребре балки, и значение у также будет другим.
По более точной формуле значение моментов инерции полусечений составит:
Iв = b'fhf(y/2)2 +b'fhf3/12 + b(y - hf)((y - hf)/2)2 + b(y - hf)3/12 = Iн = As(ho - y)2Es/Eb (321.2.3.2)
тогда, подставив имеющиеся значения, получим:
76·6(у/2)2 + 76·63/12 + 11(у - 6)(y/2 - 3)2 + 11(y - 6)3/12 = 5.09(22.3 - y)22000000/270000;
114y2 + 1368 + 2.75(y - 6)3 + 0.917(y - 6)3 = 43.704(22.3 - y)2;
у ≈ 8.08 см
Так как требуемая высота сжатой зоны при расчете на прочность больше, чем высота сжатой зоны при расчете по деформациям (разница составит примерно 7.55-7.05 = 0.5 см), то при приближенном расчете (без учета области пластических деформаций) расчетное значение высоты полки составит 6 - 0.5 = 5.5 см, тогда
Ip = 76·5.5·3.792 + 76·5.53/12 + 3.667·2.083 = 6004.2 + 1053.71 +33 = 7090.9 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 3.43 см > fu = 2 см, а значит высоту балок желательно увеличить еще.
Например, при общей высоте h = 30 см
у ≈ 10.02 см
Ip = 76·5.5·4.762 + 76·5.53/12 + 3.667·4.023 = 9470.9 + 1053.71 + 238.2 = 10762.8 см4, тогда примерный прогиб балки составит:
f = 0.83·5·9.73·5004/(384·270000·7090.9) = 1.9 см < fu = 2 см
Если произвести расчет с учетом изменяющего модуля упругости бетона, то при Еb1 = 270000/(1 + 2.8) = 71052.6 кг/см2.
76·6(у/2)2 + 76·63/12 + 11(у - 6)(y/2 - 3)2 + 11(y - 6)3/12 = 5.09(27.3 - y)22000000/71052.6;
114y2 + 1368 + 2.75(y - 6)3 + 0.917(y - 6)3 = 166.0752(27.3 - y)2;
у ≈ 14.45 см и в этом случае высота сжатой области сечения принимается без изменений, тогда
Ip = 2·27410 = 54820 см4, тогда примерный прогиб балки составит:
f = 0.96·5·9.73·5004/(384·71052.6·54820) = 1.95 см < fu = 2 см
freedocs.xyz
