Содержание
3 Слой-суглинок
— среднее значение
коэффициента Пуассона; d=0.227м
– диаметр штампа; ω=0.8 — безразмерный
коэффициент, зависящий от жесткости и
формы подошвы штампа.
;
;
;
.
S1=1.83∙10-3м;
S2=2,225∙10-3м;
кПа;
4 Слой-песок
— среднее значение
коэффициента Пуассона; d=0.227м
– диаметр штампа; ω=0.8 — безразмерный
коэффициент, зависящий от жесткости и
формы подошвы штампа.
;
;
;
.
S1=1.535∙10-3м;
S2=1,555∙10-3м;
кПа;
—
средний коэффициент относительной
сжимаемости, где
;
h1=0.5
м;
;
h2=3,5
м;
;
h3=3,5
м;
;
h4=0,3
м;
;
для суглинка мягкопластичного
;
;
суглинка тяжелого пылеватого
;
;
суглинка тяжелого пылеватого
;
;
— дополнительное давление под подошвой
фундамента.
— осадка не превышает
предельно допустимую.
Проверяем
прочность подстилающего слоя.
;
кПа, по прил. I,
табл. 8 поределяем коэффициент α=
Дополнительное
напряжение на кровле слабого слоя:
кПа.
Природное
напряжение (от собственного веса грунта)
на кровле слабого слоя:
;
;;;
.
17∙1.6+18.8∙1.3=51.64
кПа, т.к суглинок текучий находится ниже
уровня подземной воды, определяем
удельный вес грунта во взвешенном
состоянии:
;
Суммарное
напряжение на кровле слабого слоя
составит;
кПа.
Условная
ширина подошвы фундамента, опирающаяся
на кровлю слабого слоя:
Определяем
расчетное сопротивление слабого грунта:
;
.
.
кПа <
кПа.
Условие
выполняется т.е. размеры фундамента
подобраны верно.
Расчет
основания по несущей способности
Так
как на фундамент передаются горизонтальные
нагрузки, необходимо выполнить расчет
основания по несущей способности.
Приведенные
размеры по подошве фундамента:
,
,
Символом
b
обозначена сторона фундамента, в
направлении которой ожидается потеря
устойчивости основания.
.
Коэффициенты
формы подошвы фундамента:
;
;
.
Угол
δ наклона к вертикали равнодействующей
внешней нагрузки на основание:
Проверяем
условие:
,
где,
условие выполняется, следовательно
расчет ведем по формуле:
N,Nq,Nc– безразмерные коэф. определяемые по
таб.5.28[1]
N=
Nq=
Nc=
Fu=b`l`(Nl`I+NqqI`d+NcccI)=1.9∙3.08∙(0.796∙0.6∙3.08∙17+2.946∙3.42∙17.81∙2.4+8.33∙1.48∙1.8/1.5)=2753
кН
Проверяем
условие:
,
.
Условие выполняется, устойчивость
основания обеспечивается при принятых
размерах фундамента.
6. Расчет фундамента глубокого заложения.
Расчет
фундамента под первое сечение.
Проектируем
свайный фундамент с забивными
железобетонными сваями и монолитным
ростверком. Глубину заложения верха
ростверка принимаем из конструктивных
соображений 1.8 м. Высоту ростверка
принимаем равной 0.6 м. Величина заделки
сваи в ростверк принимаем 0.3 м. В качестве
естественного основания принимаем
глину тугопластичную.
Предварительно
принимаем сваю С7 – 30 длиной 7 м квадратного
сечения 0.3х0.3 м. Определим несущую
способность одной сваи
NII=2029
кН, МIIx=265
кНм, QxII=66
кН, МIIу=97
кНм, QуII=18
кН,
кН/м3
м
Lсв=0,3+0.9+3,5+2,3=7
м – длина сваи.
lсв=6.7м
– длина сваи без учета защемления в
ростверке.
— несущая способность
принятой одиночной сваи, где
— коэффициент
условий работы сваи в грунте, принимаемый
равным 1;
— коэффициенты
условий работы грунта соответственно
под нижним концом и на боковой поверхности
сваи, учитывающие влияние способа
погружения свай,
.
R
– расчетное сопротивление грунта под
нижним концом сваи
;
А
– площадь опирания на грунт сваи,
А=0,32=0,09;
u-
наружный периметр поперечного сечения
сваи,u=4∙0,3=1,2м;
— Расчетное
сопротивление i-го
слоя грунта основания на боковой
поверхности сваи;
— толщина i-го
слоя грунта, соприкасающегося с боковой
поверхностью, м.
;
h1=0.9
м;
f1=
;
h2=1,75
м;
f2=
;
h3=1,75
м;
f3=
;
h4=1,15
м;
f4=
;
h5=1,15
м;
f5=
,
где
коэффициент надежности по грунту.
Определяем
необходимое число свай
Определим нагрузку
приходящуюся на каждую сваю во внецентренно
нагруженном фундаменте:
— вес подколонника;
— вес ростверка;
—
коэффициенты надежности по нагрузке;
;
;
— вес грунта;
– расчетная
вертикальная нагрузка по подошве
ростверка;
–расчетный момент,
приведенный к подошве ростверка, в
направлении оси x;
–расчетный момент,
приведенный к подошве ростверка, в
направлении оси y;
x,
y
расстояние от центра наиболее удаленной
сваи до осей соответственно;
x=0. 45м;
45м;
y=0.6м;
кН;
кН;
;
1.2PCB=1,2∙447,99
кН > Pmax
Неравенства
выполняются, следовательно проверка
условий работы крайних свай показала,
что свайный фундамент запроектирован
рационально.
Свайный фундамент
с висячими сваями условно принимают за
массивный жесткий фундамент глубокого
заложения, контур которого ограничен
размерами ростверка, свай и некоторым
объемом грунта.
Производим проверку
сопротивления грунта основания в
горизонтальной плоскости нижних концов
свай. Определяем средневзвешенное
значение угла внутреннего трения
грунтов, прорезаемых сваями:
;
Размеры опорной
площади условного свайного фундамента:
м;
м;
Объем свайного
условного фундамента:
где
— объем свай;
— объем ростверка
и подколонника;
–объем грунта
Средневзвешенное
значение удельного веса грунта в свайном
фундаменте с учетом взвешивающего
действия воды ниже уровня подземных
вод:
;
Вес грунта в объеме
условного свайного фундамента:
;
Вес
подколонника, ростверка и свай:
;
Вертикальная
составляющая нормальных сил в уровне
нижних концов свай:
;
Краевые давления
по подошве условного свайного фундамента:
;
кНм;
кНм;
;
;
;
;
Расчетное
сопротивление несущего слоя основания:
кПа; 1. 5R=980.07
5R=980.07
Неравенства
выполняются, значит размеры фундамента
подобраны верно.
Расчет
осадки основания
Построим
эzp
и эzg
;
;
;
;
.
;
— осадка методом
эквивалентного слоя, где
— мощность
эквивалентного слоя;
— коэффициент
эквивалентного слоя приложение I,
табл. 19;
;
Определим
модуль деформации
1
слой-cуглинок
полутвердый е=0,72 β=0,62
;
;
— природное давление в середине первого
слоя от уровня подошвы условного свайного
фундамента;
;
— полное давление в середине первого
слоя.
.
S1=2,126∙10-3м;
S2=5,05∙10-3м;
кПа;
Анализ ошибок при использовании метода статических штамповых испытаний
Авторы научной статьи:
1. Штейн Александр Исаакович, начальник Инжинирингового центра, кандидат технических наук
Штейн Александр Исаакович, начальник Инжинирингового центра, кандидат технических наук
2. Черкасов Александр Михайлович, заведующий кафедрой «Транспортное строительство в экстремальных условиях», кандидат технических наук, доцент
3. Меренченко Константин Вячеславович, ассистент кафедры «Путь и путевое хозяйство»
Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский университет транспорта (МИИТ)»
В настоящее время для усиления действующих железнодорожных путей в связи с ростом осевых нагрузок и введением скоростного и высокоскоростного движения активно применяются подбалластные защитные слои (ПЗС). Конструкция ПЗС применяемая на отечественных железных дорогах регламентируется инструкцией [1], в ней указаны требования к материалу защитного слоя, его толщине и армированию. Качество ПЗС контролируется величиной статического модуля деформации Ev2, требования к которому указаны в [1], там же приведена методика проведения статических штамповых испытаний и требования к приборам для проведения этих испытаний. В последние годы метод статических штамповых испытаний так же широко применяется при контроле качества отсыпки земляного полотна транспортных сооружений. Методика штамповых испытаний считается наиболее объективной и при определении модуля деформации грунтов в естественном залегании. Настоящая статья посвящена актуальным вопросам определения модуля деформации грунтов с использованием метода статических штамповых испытаний, основным допускаемым при этом ошибкам, а также рекомендациям по эффективному применению этого метода.
В последние годы метод статических штамповых испытаний так же широко применяется при контроле качества отсыпки земляного полотна транспортных сооружений. Методика штамповых испытаний считается наиболее объективной и при определении модуля деформации грунтов в естественном залегании. Настоящая статья посвящена актуальным вопросам определения модуля деформации грунтов с использованием метода статических штамповых испытаний, основным допускаемым при этом ошибкам, а также рекомендациям по эффективному применению этого метода.
Теоретическая основа штамповых испытаний базируются на классических решениях теории упругости. Из теории упругости известно как определяется напряженное состояние полубесконечного сплошного тела, на которое действует сосредоточенная сила P, направленная вдоль оси z. Это решение получают с применением закона Гука, где напряженное состояние определяют на основе решения задачи Буссинеска. Для осесимметричной задачи, моделирующей действие силы на упругое полупространство, напряжения определяются по формулам [2]:
После подстановки в (2) выражений (1) и интегрирования, принимая также, что w (r=бесконечность)=0, получаем: F(r)=0. 2 (R в квадрате), то перемещения – пропорционально величине R . Поэтому точность определения деформаций, а именно их определяют в процессе штамповых испытаний, значительно больше зависит от однородности и изотропности исследуемого массива, чем точность определения напряжений, которые затухают на порядок быстрее.
2 (R в квадрате), то перемещения – пропорционально величине R . Поэтому точность определения деформаций, а именно их определяют в процессе штамповых испытаний, значительно больше зависит от однородности и изотропности исследуемого массива, чем точность определения напряжений, которые затухают на порядок быстрее.
Для упругого полупространства имеющего постоянные модуль упругости E, и коэффициент Пуассона M(мю), в плоскую грань которого вдавливают жесткий штамп в виде круглого цилиндра перемещение w для всех точек по круглой подошве штампа будет постоянным. При этом распределение вертикальных напряжений на контакте грунт – поверхность штампа не будет постоянным и определяется в результате решения интегрального уравнения:
В результате вертикальные напряжения передаваемые от подошвы круглого штампа на грунт определяется по формуле:
Очевидно, что минимум вертикальных контактных напряжений по поверхности штампа приходится на его ось и составляет половину средней величины.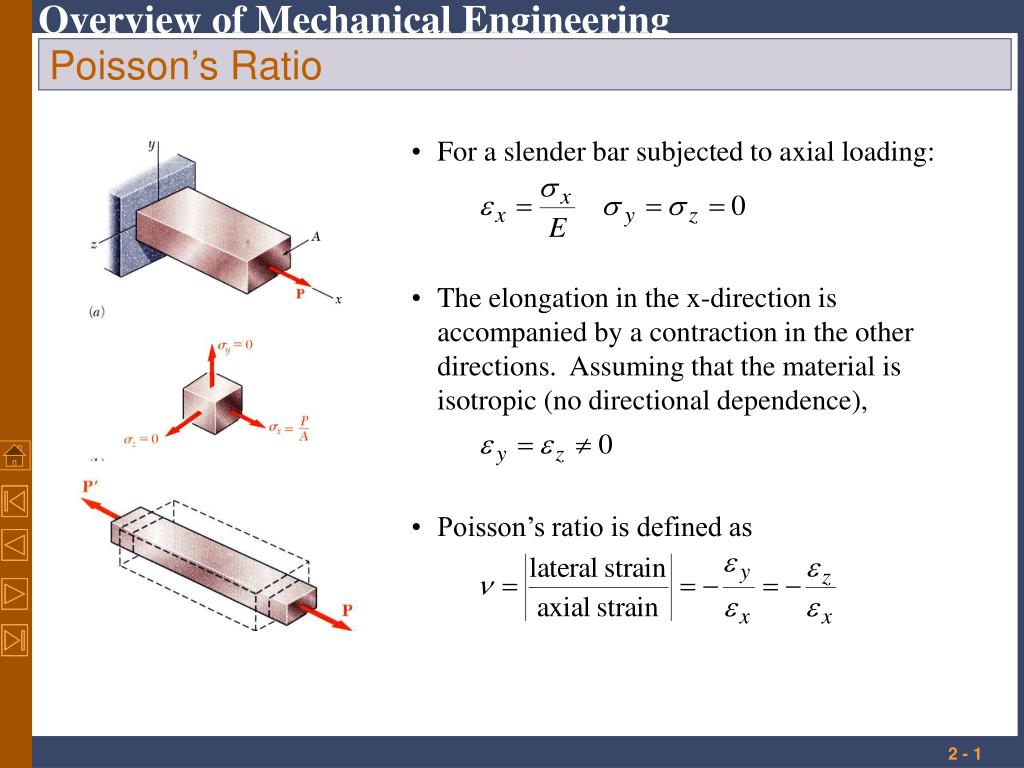 2)K1 принята осредненной для всего диапазона изменения коэффициента Пуассона. На наш взгляд такое допущение не корректно. Кроме того, по физическому смыслу, модуль упругости определяемый в ОДМ 218.5.007 [5] должен вычисляться не по второй ветви нагружения, а по ветви разгрузки. В DIN 18134:2012-04 [4], принято строить регрессионную зависимость (модель) деформаций от средней величины вертикальных контактных напряжений передаваемых от штампа на грунт в виде квадратной параболы. При этом ни одна из указанных выше методик не предусматривает проверку адекватности полученной регрессионной модели. А без этого ее использование может привести к неверной интерпретации результатов. Адекватность регрессионной модели может быть проверена по критерию Фишера.
2)K1 принята осредненной для всего диапазона изменения коэффициента Пуассона. На наш взгляд такое допущение не корректно. Кроме того, по физическому смыслу, модуль упругости определяемый в ОДМ 218.5.007 [5] должен вычисляться не по второй ветви нагружения, а по ветви разгрузки. В DIN 18134:2012-04 [4], принято строить регрессионную зависимость (модель) деформаций от средней величины вертикальных контактных напряжений передаваемых от штампа на грунт в виде квадратной параболы. При этом ни одна из указанных выше методик не предусматривает проверку адекватности полученной регрессионной модели. А без этого ее использование может привести к неверной интерпретации результатов. Адекватность регрессионной модели может быть проверена по критерию Фишера.
Анализ теории и предпосылок, принятых при выводе расчетной формулы (6), показывает и слабые стороны построенной на ее основе методики статических штамповых испытаний. Рассмотрим некоторые из них.
1). Формулы (5), (6) получены для упругого однородного изотропного полупространства, то есть не учитывается возможность наличия различных слоев грунтов с разными физико-механическими свойствами.
2). В соответствие с граничными условиями, использованными при выводе этих формул, напряжения и особенно деформации затухают бесконечно далеко от точки приложения нагрузки. В реальности, видимо затухание деформаций происходит существенно раньше, так как грунты имеют некоторую структурную прочность. Ниже приведены результаты численного моделирования штамповых испытаний двухслойного грунтового массива, штампом диаметром 0,3 м. Верхний слой представлен крупнозернистым песком различной толщины. Нижний – суглинком. Принятые характеристики грунтов представлены в таблице 1.
Расчеты проводились методом конечных элементов (МКЭ) с применением программных комплексов Plaxis 2D и GeoStudio. В силу специфических особенностей алгоритма Plaxis 2D оказалось возможным использовать только для решения настоящей задачи в линейной постановке. Поэтому приведены результаты расчетов с применением комплекса GeoStudio (SIGMA/W Analysis).
Первая задача, которая решалась, это определение размеров расчетной модели. Это необходимо, так как требуется обеспечить сходимость к точному решению по величинам деформаций. Для этого подбирались такие размеры модели, чтобы деформация, вычисленная по формуле (6), для песка при средней величине вертикальных контактных напряжений от штампа равной p = 200 кПа, составляла 1,092. Разница в деформациях с учетом требований к точности измерений принята +/- 0,01 мм. Высота песчаного столба составила 13 м. Вертикальная деформация составила 1,082 мм, что соответствует модулю упругости Е = 40,357 МПа (ошибка меньше 1%). Для суглинка по (6) при средней величине вертикальных контактных напряжений от штампа на грунт p = 200 кПа вертикальная деформация составляет 2,034 мм, а по МКЭ – 1,996, что соответствует модулю 20,366 МПа. То есть высоты грунтового массива (13 м) из суглинка для достижения точности мм не достаточно (ошибка почти 2%).
Это необходимо, так как требуется обеспечить сходимость к точному решению по величинам деформаций. Для этого подбирались такие размеры модели, чтобы деформация, вычисленная по формуле (6), для песка при средней величине вертикальных контактных напряжений от штампа равной p = 200 кПа, составляла 1,092. Разница в деформациях с учетом требований к точности измерений принята +/- 0,01 мм. Высота песчаного столба составила 13 м. Вертикальная деформация составила 1,082 мм, что соответствует модулю упругости Е = 40,357 МПа (ошибка меньше 1%). Для суглинка по (6) при средней величине вертикальных контактных напряжений от штампа на грунт p = 200 кПа вертикальная деформация составляет 2,034 мм, а по МКЭ – 1,996, что соответствует модулю 20,366 МПа. То есть высоты грунтового массива (13 м) из суглинка для достижения точности мм не достаточно (ошибка почти 2%).
3). Методика построена на основе линейной теории упругости и не учитывает возможность появления пластических деформаций, которые возникают по краям штампа и развиваются вглубь слоя грунта, в то время как под штампом формируется уплотненное ядро. То есть методика по ГОСТ 20276 [3] не учитывает физическую нелинейность грунта, что особенно важно при нагрузках выше начального критического давления и дает искаженное значение модуля деформации, а также не учитывает развитие зон сдвигов. Поэтому, если расчеты конструкции планируется производить с применением упруго-пластических моделей, применение модуля деформации, полученного с применением штамповых испытаний, при нагрузках существенно превышающих начальное критическое давление, приведет к завышенным величинам деформаций. Наличие пластических деформаций приводит к изменению эпюры вертикальных контактных напряжений под штампом – исчезают зоны «бесконечных» напряжений по краям штампа и в целом контактные напряжения распределяются более равномерно. На графиках, представленных на рисунке 1, показаны зависимости вычисленного по формуле (6) секущего модуля деформации. Величина деформации (вертикального перемещения) штампа w определялась на основе численного моделирования. Горизонтальные линии показывают линейное (упругое) решение для однослойного грунтового массива.
То есть методика по ГОСТ 20276 [3] не учитывает физическую нелинейность грунта, что особенно важно при нагрузках выше начального критического давления и дает искаженное значение модуля деформации, а также не учитывает развитие зон сдвигов. Поэтому, если расчеты конструкции планируется производить с применением упруго-пластических моделей, применение модуля деформации, полученного с применением штамповых испытаний, при нагрузках существенно превышающих начальное критическое давление, приведет к завышенным величинам деформаций. Наличие пластических деформаций приводит к изменению эпюры вертикальных контактных напряжений под штампом – исчезают зоны «бесконечных» напряжений по краям штампа и в целом контактные напряжения распределяются более равномерно. На графиках, представленных на рисунке 1, показаны зависимости вычисленного по формуле (6) секущего модуля деформации. Величина деформации (вертикального перемещения) штампа w определялась на основе численного моделирования. Горизонтальные линии показывают линейное (упругое) решение для однослойного грунтового массива. Как видно, они с хорошей точностью соответствуют заданным модулям деформации для крупнозернистого песка и суглинка соответственно.
Как видно, они с хорошей точностью соответствуют заданным модулям деформации для крупнозернистого песка и суглинка соответственно.
Рисунок 1 – Изменение модуля деформации определенного на основе численного моделирования штамповых испытаний в зависимости от величины среднего вертикального контактного напряжения передаваемого от штампа на грунт
Упруго-пластическое решение, с использованием модели грунта Мора-Кулона, показывает, что модуль деформации в этом случае сильно зависит от величины контактных напряжений в грунте под штампом. Объясняется это развитием зон предельного равновесия, которые зарождаются под кромками штампа. Для песка, практически не имеющего структурной прочности, это влияние ощущается с самого начала нагружения. Для суглинка, это влияние проявляется существенно позже, начиная с вертикальных контактных напряжений приблизительно равных p = 150 кПа.
Для определения расчетного диапазона нагрузок на штамп было определено предельное давление (давление при котором происходит полная потеря несущей способности грунта под штампом) [11]:
Результаты расчетов по формуле (7) представлены в таблице 2.
Таблица 2 – Коэффициенты несущей способности и результаты расчетов предельного давления:
Полученная нагрузка pн конечно не допустима при штамповых испытаниях и в данном случае использована только для численного моделирования. Эта нагрузка приводит более чем к двухкратному снижению модуля деформации (рисунок 1).
В качестве примера на рисунках 2 … 4 приведены результаты расчета двухслойного грунтового массива состоящего из 1 м крупнозернистого песка и 12 м суглинка при среднем вертикальном контактном напряжении под штампом p = 200 кПа. На рисунках 2 и 3 показаны изолинии горизонтальных деформаций. Из этих рисунков видно, что расчетные максимальные горизонтальные деформации при применении упруго-пластичной модели Мора-Кулона в 2,5 раза больше чем в линейной. Вертикальные деформации при применении упруго-пластической задачи более чем 1,5 раза превосходят деформации для линейной задачи. Вообще влияние толщины исследуемого слоя (песка) на его модуль деформации можно увидеть из графика, приведенного на рисунке 1. При толщине слоя крупного песка от 13 до 3 м можно считать, что в начале нагружения модуль деформации основания практически равен модулю деформации крупного песка. С ростом нагрузки на штамп модуль деформации начинает снижаться, с учетом того, что на суммарную деформацию начинают существенно влиять деформации нижележащих слоев грунта, а развивающиеся зоны предельного равновесия грунта. Следует отметить, что на начальной стадии нагружения ( p = 100…150 кПа) модуль деформации снижается достаточно быстро, при этом его величина может уменьшиться на 25%. В дальнейшем, с ростом нагрузок снижение модуля продолжается, но значительно менее интенсивно.
При толщине слоя крупного песка от 13 до 3 м можно считать, что в начале нагружения модуль деформации основания практически равен модулю деформации крупного песка. С ростом нагрузки на штамп модуль деформации начинает снижаться, с учетом того, что на суммарную деформацию начинают существенно влиять деформации нижележащих слоев грунта, а развивающиеся зоны предельного равновесия грунта. Следует отметить, что на начальной стадии нагружения ( p = 100…150 кПа) модуль деформации снижается достаточно быстро, при этом его величина может уменьшиться на 25%. В дальнейшем, с ростом нагрузок снижение модуля продолжается, но значительно менее интенсивно.
Описанные выше особенности определения модуля деформации с применением штамповых испытаний будут оказывать еще большее влияние на результат испытаний при увеличении размеров штампа.
4). Коэффициент Пуассона входящий в формулы (5) и (6) не определяют при штамповых испытаниях, а принимают равным неким осредненным значениям в зависимости от вида грунта. Это также вносит определенную ошибку в результаты определения модуля деформации. Еще хуже обстоит дело в DIN 18134:2012-04 [4], ОДМ 218.5.007 [5] и других подобных документах [6, 7, 8, 9, 10]. В этих документах для всех видов грунтов принято одно осредненное значение , приблизительно равное 0,21.
Это также вносит определенную ошибку в результаты определения модуля деформации. Еще хуже обстоит дело в DIN 18134:2012-04 [4], ОДМ 218.5.007 [5] и других подобных документах [6, 7, 8, 9, 10]. В этих документах для всех видов грунтов принято одно осредненное значение , приблизительно равное 0,21.
Какие выводы можно сделать из проведенного выше анализа? Для определения модуля деформации при применении методики штамповых испытаний следует иметь достаточно полную информацию о геологическом строении и инженерно-геологических элементах его складывающих. Кроме того, необходимо внимательно подходить к назначению максимальных нагрузок на штамп. Они не должны существенно превышать расчетные. Если исследуемый слой имеет не большую толщину, а подстилающий слой имеет существенно большую деформативность, для определения модуля деформативности исследуемого слоя целесообразно провести решение обратной задачи, по известным деформациям и геологической информации. И последнее. Определять деформации грунта под штампом следует с как можно более высокой точностью, а также обеспечить исключение систематических и не систематических ошибок за счет тарировки и калибровки датчиков, а также выполнения параллельных измерений.
Использованнная литература:
1. Инструкция по устройству подбалластных защитных слоев при реконструкции (модернизации) железнодорожного пути, утв. распоряжением ОАО «РЖД» от 12.12.2012 №2544р.
2. Кац А.М. Теория упругости. 2-е изд., стер. – СПб.: Издательство «Лань», 2002. – 208 с.
3. ГОСТ 20276-2012. Грунты. Методы полевого определения характеристик прочности и деформируемости.
4. DIN 18134:2012-04. Грунты строительные. Испытания и приборы для испытания. Метод давления с применением грузовой плиты.
5. ОДМ 218.5.007-2016. Методические рекомендации по определению модуля упругости статическим штампом.
6. ГОСТ Р (проект, первая редакция). Штамповые испытания земляного полотна для высокоскоростных железнодорожных линий. Технические требования.
7. ПНСТ (проект). 1.2.418-1.023.18. Дороги автомобильные общего пользования. Показатели деформативности конструктивных слоев дорожной одежды из несвязных материалов и грунтов земляного полотна. Технические требования и методы определения.
Технические требования и методы определения.
8. СТО АВТОДОР 10.3-2014. Метод оценки качества несущих оснований из необработанных вяжущими материалов по деформативности их поверхности на стадии приемочного контроля при устройстве дорожных одежд.
9. СТО АВТОДОР 10.3-2018. Метод оценки качества слоев оснований дорожных одежд из необработанных вяжущими материалов по деформативности их поверхности на стадии строительного контроля.
10. СТО АВТОДОР 2.31-2018. Требования к показателям деформативности слоев оснований дорожных одежд из необработанных вяжущими материалов.
11. СП 22.13330.2016. Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01-83*.
Остались вопросы? Свяжитесь с нами!
Оставьте заявку, наш специалист свяжется с Вами
и проконсультирует по всем вопросам.
| Получить консультацию |
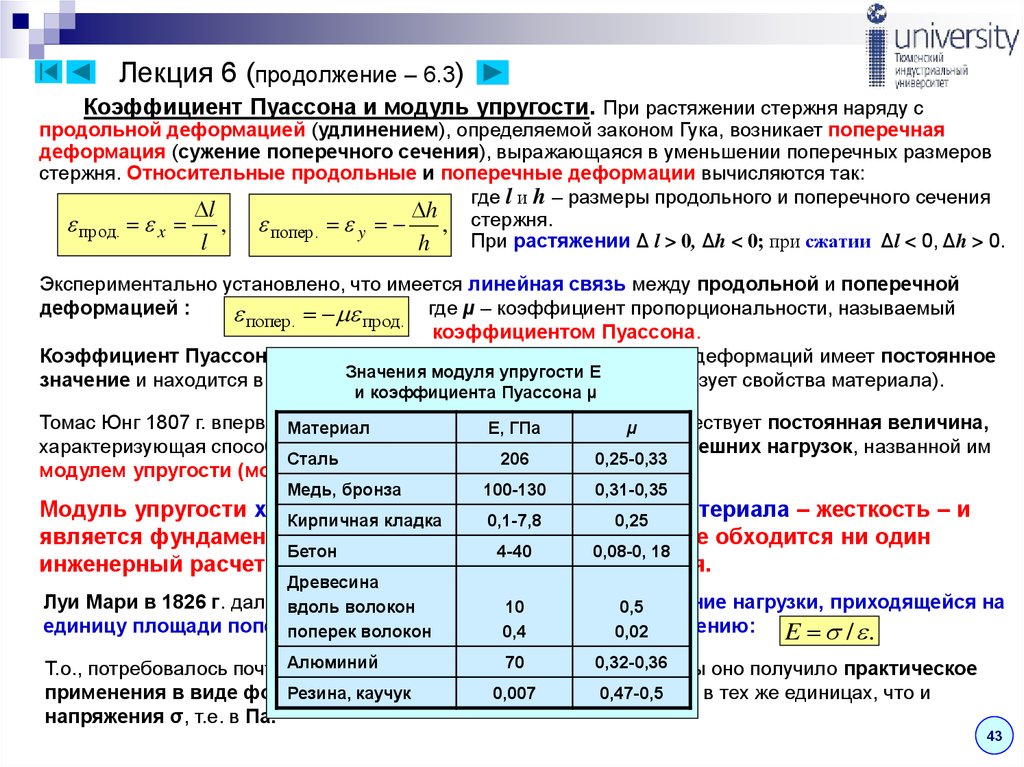
Коэффициент Пуассона
Когда образец материала растягивается в одном направлении, он становится тоньше в поперечном направлении, а если образец сжимается в одном направлении, он становится толще в поперечном направлении.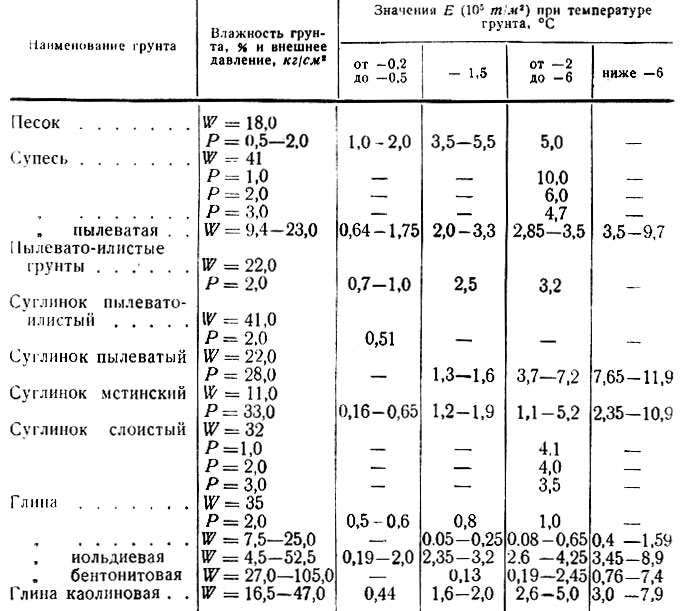
Коэффициент Пуассона равен
- отношение относительной деформации сжатия (поперечной, поперечной или радиальной деформации) по нормали к приложенной приложенная нагрузка
Poisson’s Ratio can be expressed as
μ = — ε t / ε l (1)
where
μ = Poisson’s ratio
ε t = поперечная деформация (м/м, фут/фут)
ε l = продольная или осевая деформация (м/м, фут/фут)
Деформация твердый из-за стресса».
Продольная (или осевая) деформация может быть выражена как
ε L = DL / L (2)
, где
ε L = 5592020 2 ε L = 55. безразмерный — или м/м, фут/фут)
dl = изменение длины (м, фут)
L = начальная длина (м, фут)
2 Сокращение0010 (или поперечная, боковая или радиальная) деформация может быть выражена как
ε T = DR / R (2)
, где
ε T = Transfvers (безразмерный — или м/м, фут/фут)
dr = изменение радиуса (м, фут)
r = начальный радиус (м, фут)
Пример — растяжение алюминия3 9012 Алюминиевый стержень длиной
10 м и радиус 100 мм (100 10 -3 м) растянутый 5 мм (5 10 -3 м) . Радиальное сжатие в поперечном направлении можно рассчитать, комбинируя уравнение (1) и (2) до
Радиальное сжатие в поперечном направлении можно рассчитать, комбинируя уравнение (1) и (2) до
μ = — ( DR / R ) / ( DL / L ) (3)
— и переосмысление в
9002
— . — μ r дл/л (3b)
With Poisson’s ratio for aluminum 0.334 — the contraction can be calculated as
dr = — 0.334 ( 100 10 -3 m ) ( 5 10 -3 m ) / (10 m)
= 1.7 10 -5 m
= 0.017 mm
Коэффициент Пуассона для распространенных материалов
Для большинства распространенных материалов коэффициент Пуассона находится в диапазоне 0 — 0,5 . Типичные коэффициенты Пуассона для некоторых распространенных материалов указаны ниже.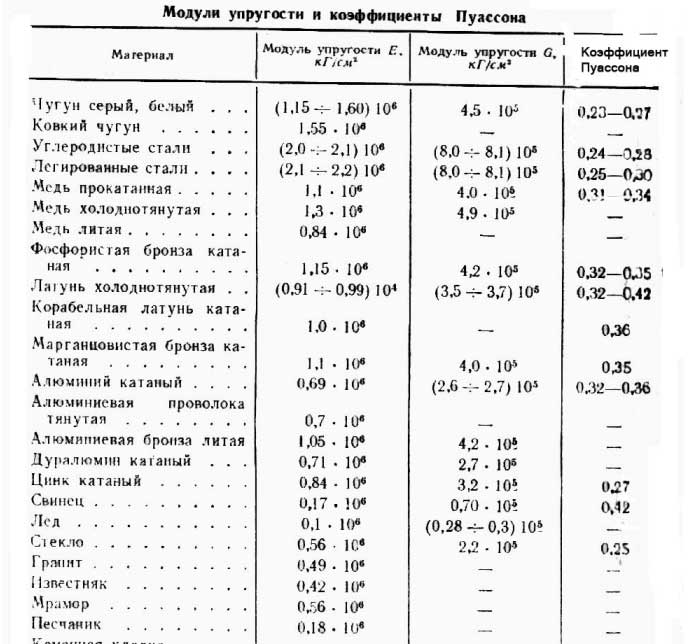
| Material | Poisson’s Ratio — μ — |
|---|---|
| Upper limit | 0.5 |
| Aluminum | 0.334 |
| Aluminum, 6061-T6 | 0.35 |
| Aluminum, 2024-T4 | 0.32 |
| Beryllium Copper | 0.285 |
| Brass, 70-30 | 0.331 |
| Brass, cast | 0.357 |
| Bronze | 0.34 |
| Clay | 0.41 |
| Concrete | 0.1 — 0.2 |
| Copper | 0.355 |
| Cork | 0 |
| Glass, Soda | 0.22 |
| Glass, Float | 0.2 — 0.27 |
| Granite | 0.2 — 0.3 |
| Ice | 0.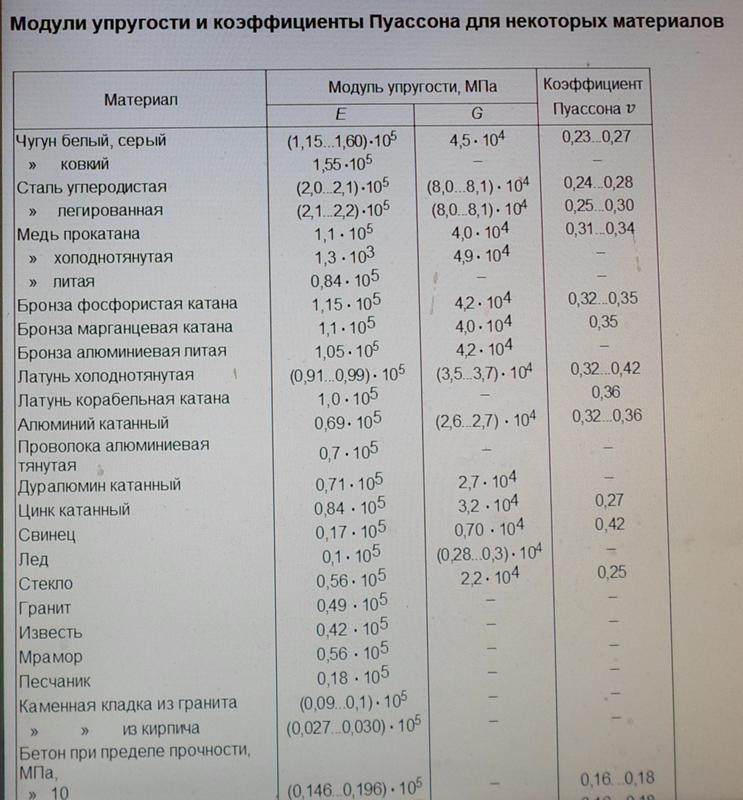 33 33 |
| Inconel | 0.27 — 0.38 |
| Iron, Cast — gray | 0.211 |
| Iron, Cast | 0.22 — 0.30 |
| Iron, Ductile | 0.26 — 0.31 |
| Iron, Malleable | 0.271 |
| Lead | 0.431 |
| Limestone | 0.2 — 0.3 |
| Magnesium | 0.35 |
| Magnesium Alloy | 0.281 |
| Мрамор | 0,2 — 0,3 |
| Молибден | 0,307 |
| 30233 | |
| Nickel Silver | 0.322 |
| Nickel Steel | 0.291 |
| Polystyrene | 0.34 |
| Phosphor Bronze | 0.359 |
| Rubber | 0.48 — ~0.5 |
| Нержавеющая сталь | 0,29 |
| Супесь | 0,31 |
| Песчаная глина | 0,37 | 8 Сталь0233 | 0. 305 305 |
| Steel, cast | 0.265 |
| Steel, Cold-rolled | 0.287 |
| Steel, high carbon | 0.295 |
| Steel, mild | 0.303 |
| Titanium (99.0 Ti) | 0.32 |
| Wrought iron | 0.278 |
| Z-nickel | 0.36 |
| Zinc | 0.331 |
Коэффициент Пуассона для Boneheads, а также часто задаваемые вопросы
Коэффициент Пуассона — это значение, которое определяет степень сжатия, которое происходит, когда что-то растягивается, или степень расширения, когда объект сжимается. Сокращение всегда измеряется в соотношении 90 o к силе растяжения или сжатия.
Проще говоря, когда объект растягивается, он становится тоньше, а когда сжимается, он становится толще. Это известно как эффект Пуассона.
Коэффициент Пуассона — это просто отношение деформации в направлении растяжения к перпендикулярной деформации. Деформация определяется как деформация, вызванная напряжением.
Деформация определяется как деформация, вызванная напряжением.
Отношение названо в честь Симеона Пуассона, французского инженера, физика и математика, который определил эффект Пуассона в своей книге 1811 года Traité de Mécanique – Механика материалов.
Коэффициент Пуассона можно найти, измерив разницу в толщине и длине при растяжении или сжатии, а затем используя эти значения для расчета деформации в каждом направлении. Чем ниже значение, тем более устойчив материал к деформации. Для большинства материалов значения обычно находятся в диапазоне от 0,1 до 0,5.
Теперь, когда у нас есть очень простое определение, давайте посмотрим на вещи немного подробнее.
Техническое определение коэффициента Пуассона
С технической точки зрения коэффициент Пуассона представляет собой отношение деформации поперечного сжатия или расширения (перпендикулярно) к продольной деформации (т. е. в том же направлении, что и приложенная сила).
Коэффициент Пуассона обозначается греческой буквой nu ( μ ).
Математически:
μ = – ε t / ε l
Given that:
μ = Poisson’s ratio
ε t = transverse (perpendicular ) деформация
ε l = продольная деформация
Знак минус учитывает тот факт, что деформация растяжения принимается положительной, а деформация сжатия — отрицательной.
Продольная деформация может быть рассчитана с использованием следующей формулы:
ε L = DL / L
. деформация
dl = разность длин (м)
L = статическая длина (м)
Поперечная деформация может быть рассчитана по следующей формуле:
ε t = dr / r
Given that:
ε t = transverse strain
dr = difference in radius (m)
r = начальный радиус (м)
Общие значения коэффициента Пуассона
В этой таблице приведены значения для некоторых часто используемых материалов:
| Материал | Коэффициент Пуассона |
| – μ – | |
| Максимальное значение: | 0,5 |
| Алюминий | 0,334 |
| Алюминий, 6061-T6 | 0,35 |
| Алюминий, 2024-T4 | 0,32 |
| Бериллиевая медь | 0,285 |
| Латунь, 70-30 | 0,331 |
| Литая латунь | 0,357 |
| Бронза | 0,34 |
| Глина | 0,41 |
| Бетон | 0,1 – 0,2 |
| Медь | 0,355 |
| Пробка | 0 |
| Стекло, сода | 0,22 |
| Стекло, поплавок | 0,2 – 0,27 |
| Гранит | 0,2 – 0,3 |
| Лед | 0,33 |
| Инконель | 0,27 – 0,38 |
| Чугун, литой – серый | 0,211 |
| Железо, литье | 0,22 – 0,30 |
| Чугун, ковкий | 0,26 – 0,31 |
| Чугун, ковкий | 0,271 |
| Свинец | 0,431 |
| Известняк | 0,2 – 0,3 |
| Магний | 0,35 |
| Магниевый сплав | 0,281 |
| Мрамор | 0,2 – 0,3 |
| Молибден | 0,307 |
| Монель-металл | 0,315 |
| Нейзильбер | 0,322 |
| Никелированная сталь | 0,291 |
| Полистирол | 0,34 |
| Фосфорная бронза | 0,359 |
| Резина | 0,48 – ~0,5 |
| Песок | 0,29 |
| Песчаный суглинок | 0,31 |
| Песчаная глина | 0,37 |
| Нержавеющая сталь 18-8 | 0,305 |
| Сталь литая | 0,265 |
| Сталь холоднокатаная | 0,287 |
| Сталь высокоуглеродистая | 0,295 |
| Сталь мягкая | 0,303 |
| Титан (99,0 Ti) | 0,32 |
| Кованое железо | 0,278 |
| Z-никель | 0,36 |
| Цинк | 0,331 |
Источник таблицы: https://www.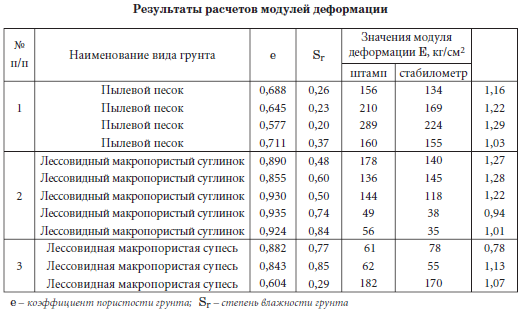 engineeringtoolbox.com
engineeringtoolbox.com
Спайдер-диаграмма: Влияние выбранных добавок компонентов стекла на коэффициент Пуассона определенного базового стекла.
Часто задаваемые вопросы
- Является ли коэффициент Пуассона постоянным для материала?
Пока материал точно соответствует протестированному, тогда да, он останется неизменным для этого материала.
- Почему важен коэффициент Пуассона?
Понимание влияния напряжения на материал имеет ряд важных применений, особенно в машиностроении.
Например, прецизионные детали, предназначенные для аэрокосмической техники, должны выдерживать значительные нагрузки без серьезной деформации. Крайне важно выбрать правильный материал, и коэффициент Пуассона поможет в этом выборе.
Другими важными областями применения являются проектирование систем трубопроводов высокого давления, особенно тех, которые транспортируют легковоспламеняющиеся или взрывоопасные жидкости или газы.
- Что такое коэффициент Пуассона в бетоне?
Соотношение для бетона варьируется от 0,1 для высокопрочного бетона до 0,2 для более слабых смесей.
- Имеет ли коэффициент Пуассона единицы измерения?
Нет, считается безразмерным.
- Является ли коэффициент Пуассона отрицательным
Положительный результат для большинства материалов, так как к формуле добавляется знак минус, чтобы получить положительный результат, когда поперечное сечение материала уменьшается под действием растягивающей силы. Некоторые редкие материалы (ауксетики) демонстрируют увеличение поперечного сечения при растяжении. Они будут иметь отрицательный коэффициент Пуассона.
- Что, если коэффициент Пуассона равен нулю?
Теоретически материал с нулевым отношением не будет демонстрировать поперечную деформацию при приложении осевой деформации.