Расчет забутовки: Расчет объема и массы раствора для забутовки футляра

Сравнение теоретических данных напряженно-деформированного состояния крестового свода с данными численного эксперимента



В расчетах конструкций сводчатых перекрытий целесообразно использовать метод конечно-элементного моделирования, который позволяет учесть не только пространственную работу конструкций, но и особенности материала. Для того, чтобы использовать такой метод расчета? необходимо удостовериться в его корректности. В настоящей работе проведено сравнение теоретических данных по распределению напряжений в теле крестового свода и прогибов с данными, полученными при расчёте и моделировании конечно-элементной модели в программном комплексе Abaqus.

Ключевые слова: крестовый свод, кирпичный свод, конечно-элементное моделирование.

Большое количество зданий, в которых применены кирпичные своды в качестве перекрытий или покрытий, требуют ремонта, реставрации или восстановления. За длительный период службы конструкции испытали различные виды воздействий (нагрузки статические и динамические, атмосферные воздействия, подвижка опор), которые могли сказаться на несущей способности и целостности конструкции. Для проведения качественных и эффективных строительных работ на таких конструкциях, а также с целью осуществления правильной и безопасной дальнейшей эксплуатации необходимо представлять действительный характер распределения напряжений в теле свода, определять расположение наиболее нагруженных и ослабленных частей свода, а также идентифицировать серьёзность дефектов, проявляющихся на поверхностях свода.

Свод — тип перекрытия или покрытия здания или сооружения, образованный наклонными поверхностями (прямолинейными или криволинейными) и ограниченный стенами, балками или столбами, отличается от других типов перекрытия наличием распора, работает преимущественно на сжатие. Распор свода воспринимается обычно затяжками, контрфорсами, стенами, столбами, может взаимоуравновешиваться распором соседних сводов.

Достоинства распорных систем:

– высокая пространственная жесткость;

– терпимость к нарушениям сплошности кладки;

– большая несущая способность по сравнению с плоскими перекрытиями;

– возможность искусственного перераспределения усилий между элементами.

В настоящее время кирпичные своды вытеснены железобетонными и металлическими конструкциями, поэтому вопрос о проектировании новых сводчатых конструкций не стоит. Тем не менее, всё большее количество инженеров и учёных вновь заинтересовано в нахождении более простого способа расчёта сводов.

В 1911 году инженер Н. К. Лахтин в своей книге писал: «Сводчатые же конструкции, отличающиеся своим чрезвычайным разнообразием, разработаны в отношении их расчета сравнительно слабо. Имеющиеся в руководствах по строительной механике и статике сооружений отделы о сводах страдают неполнотой и схематичностью, а разбросанные в периодической литературе отдельные журнальные статьи о расчетах сводов не дают надлежащего освещения этого вопроса…» [1]. Как тогда, так и теперь расчеты сводов имеют только приближенный характер, а современные нормативные документы [10] не дают исчерпывающих рекомендаций по поверочным расчётам существующих кирпичных сводов, нуждающихся в реставрации и ремонте. В настоящее время стоит вопрос о сохранении большего количества существующих исторических построек, но это возможно только в случае их правильного технического оснащения, прокладка современных инженерных сетей необходима для создания пригодной среды для работы или жизни человека в таких зданиях. Часто для правильного монтажа инженерных сетей необходимо пробивать проемы в строительных конструкциях, в том числе и в покрытиях. Устройство проема ведет к ослаблению конструкции, поэтому важно представлять схему распределения напряжений в конструкции, их значения, и на основании этих данных принимать правильные проектные решения.

В соответствии с современными нормами проектирования, при расчёте кирпичных сводов используют метод предельных состояний. Расчет заключается в проверке опасных сечений свода, которые находят при построении эпюр моментов и поперечных усилий по уравнениям статики. При этом пространственную конструкцию свода приводят к системе элементарных плоских арок. Такой способ усложняет оценку пространственной работы конструкции, ведёт к большому количеству приближений в расчётах и увеличивает погрешность результата. Также сложность в расчет вносит разномодульность составляющих кирпичной кладки и, как следствие, анизотропия в направлении к вертикальным и горизонтальным растворным швам, в связи с чем прочностные характеристики кладки могут варьироваться в зависимости не только от марки кирпича и раствора, но и от способа укладки, заполнения растворных швов, перевязки и много другого. От этих же характеристик могут зависеть и процессы разрушений в кирпичных кладках. Можно выделить три возможных места разрушения кирпичной кладки: по кирпичу, по раствору и по зоне контакта материалов.

Численное моделирование позволяет оценить пространственную работу кирпичных сводов с учетом объемного напряженного состояния материала. В статье [7] рассмотрены модели сводов с различными способами учета характеристик кирпичной кладки:

1. Гомогенная модель — сплошной объём конструкции в котором материал задается однородным и анизотропным;
2. Гомогенную модель с уточняющими участками, моделируемыми как конструкция «кирпич+раствор»:

1 шаг — конструкция моделируется и анализируется как монолитное упругое тело с учётом опорной жесткости;

2 шаг — один из опасных участков моделируется как конструкция «кирпич+раствор» с использованием граничных условий от монолитной упругой арки и проводится анализ;

3 шаг — новые граничные условия от участка прикладываются к арке.

Порядок повторяется для всех опасных участков, включая новые, если они возникают.

3. Упрощенная гетерогенная модель — представляет собой раздробленную модель, в которой размеры кирпича увеличивают на размер растворного шва, а растворный шов и граница контакта сводятся в единый плоский связующий элемент;
4. Гетерогенная модель — подробная модель, в которой граница контакта между кирпичом и раствором представлена как дополнительный элемент с фиктивной жесткостью и является потенциальной границей разрушения кладки.

На данный момент проводятся попытки моделирования каменных сводов с помощью различных программных комплексов, основанных на методе конечно-элементного моделирования.

Используя программные комплексы для моделирования кирпичных сводов также можно столкнуться с рядом сложностей, таких как:

– определение адекватности модели и достоверности результатов расчёта;

– временные затраты на построение более точных моделей;

– подбор формы и размеров конечных элементов и учёт их влияния на результаты, при неудачном выборе типа конечного элемента в расчете могут накапливаться погрешности, которые значительно влияют на конечный результат.

В статье [6] описана попытка моделирования кирпичного свода в программном комплексе SCAD, при которой удалось оценить вид распределения основных напряжений, но моделирование формы конструкции оказалось затруднительно. Моделирование производилось с помощью пластинчатых элементов, расчетная схема конструкции представлена комбинацией двух расчетных схем: монолитного упругого тела и конструкции «кирпич плюс раствор». По результатам исследования был сделан вывод о том, что данная схема может использоваться, но в более подходящих для такой задачи программных комплексах, таких как ANSYS или Abaqus.

ПК Abaqus многофункционален и может использоваться для решения задач с учетом всех видов нелинейности, он также оснащена удобным графическим модулем, в котором выполняется моделирование конструкции и визуализация расчётов. Для того чтобы определить возможность расчёта кирпичных сводов в данном ПК было проведено моделирование крестового свода и его расчёт.

Крестовые своды образуются при пересечении двух коробчатых сводов под прямым углом и отсечении внутренних частей данных сводов таким образом, что давление передается на углы и отсутствует давление на стены. В [1–3] представлены выкладки по расчёту и моделированию кирпичных крестовых сводов, согласно данным работам нагрузки в крестовом своде распределяются следующим образом:

– на рисунке 1 представлена эпюра давления элементарных полуарок в опорном контуре и в ребре:

Рис. 1. Крестовый свод: а- рабочая схема, б — эпюра давления (распора) элементарных полуарок в опорном контуре, в — эпюра элементарных распоров и давлений в ребре

– на рисунке 2 представлены эпюры моментов и поперечных сил в ребре крестового свода:

Рис. 2. Эпюры моментов и поперечных сил в диагональном ребре крестового свода

– на рисунке 3 представлены висячие зоны свода и картограмма напряжений:

Рис. 3. Распределение сжимающих усилий и напряжений в крестовом своде: а — модель напряженного состояния, б — картограмма напряжений (МПа)

Опасные зоны элементарной арки свода были выявлены многими веками наблюдения, конструирования и расчёта сводов. Таким образом, чаще всего слабыми местами свода является замок, самыми нагруженными зонами — пяты свода, висячие зоны расположены в центре пролета у опорного контура конструкции. Расположение трещин, типичных для данного вида сводов, представлено на рисунке 4.

Рис. 4. Характерное распространение трещин в крестовом своде: а — общий вид конструкции, б — вид сбоку, в — вид сверху

Для моделирования и расчёта был выбран крестовый свод пролётом между пятами 5,5 м, толщиной 250 мм, в двух вариантах: с забутовкой и без. Нагрузка, равная 1 т/м², равномерно распределена по наружной поверхности свода. Свод смоделирован гомогенной моделью, в связи с тем, что она требует меньше исходных данных, значительно упрощает моделирование и ускоряет обработку данных при расчёте.

Рис. 5. Модель крестового свода: а — без забутовки, б — с забутовкой

Характеристики материала:

– удельный вес кладки: γ = 1,8 т/м³;

– расчетное сопротивление кладки сжатию — R = 1 МПа;

– расчетное сопротивление кладки растяжению — R_tb= 0,04–0,05 МПа.

– модуль упругости кладки (начальный модуль деформации) — E = 909,09 МПа, рассчитан в соответствии с нормами [10].

– коэффициент Пуассона: 𝜇 = 0,2.

– коэффициент линейного расширения кладки: 𝛼 = 0,000005.

Рис. 6. Изополя максимальных напряжений в своде без забутовки: а — шкала вычисленных значений главных напряжений (Па), б — вид сверху, в — вид снизу

Рис. 7. Изополя максимальных напряжений в своде с забутовкой: а — шкала вычисленных значений главных напряжений (Па), б — вид сверху, в — вид снизу

Рис. 8. Эпюры моментов в диагональном ребре крестового свода: а — без забутовки, б — с забутовкой

При сравнении графического представления напряжений (рис.6,7) можно отметить, что в крестовом своде без забутовки на нижней поверхности свода в замковой части диагональных рёбер наблюдается концентрация напряжений. В своде с забутовкой концентрация напряжения в этих местах отсутствует. Это подтверждает, что роль забутовки очень важна в таких конструкциях. При увеличении нагрузки в приопорных зонах эпюра моментов приближается к идеальной линии свода.

Появление трещин начинается там, где предельное сопротивление растяжению кирпичной кладки меньше, чем растягивающие усилия, а в тех местах, где расчётное сопротивление на сжатие меньше сжимающих усилий может наблюдаться раздробление материала. Распространение максимальных и минимальных напряжений на планах изополей свода с забутовкой совпадают со схемой распространения трещин типичных для крестовых сводов (рис.4).

Сравнение показало сходимость в теоретических данных, выведенных многими веками исследования, и данных, полученных путём численного моделирования конструкции в ПК Abaqus. Это указывает на возможность использования данной программы для дальнейших расчётов. Для более точного определения верности моделирования необходимо сравнение численных результатов расчета в программе и натурного испытания конструкции.

Литература:

1. Лахтин Н. К. Расчет арок и сводов. Руководство к аналитическому и графическому расчету арочных и сводчатых перекрытий. — М.: Студенческое Издательское Общество при Императорском Техническом Училище, 1911. — 468 с.
2. Бессонов Г. Б. Исследование деформаций, расчет несущей способности и конструктивное укрепление древних распорных систем. — М.: Союзреставрация, 1989. — 171 с.
3. Бернгард В. Р. Арки и своды. Руководство к устройству и расчету арочных и сводчатых перекрытий. — СПб.: Типография Ю. Н. Эрлих, 1901. — 128 с.
4. Reccia E., Milani G., Cecchi A., Tralli A. (2014) Full 3D homogenization approach to investigate the behavior of masonry arch bridges: The Venice trans-lagoon railway bridge. Construction and Building Materials. 2014. No. 66 pp. 567–586.
5. Milani E., Milani G., Tralli A. (2008). Limit analysis of masonry vaults by means of curved shell Finite Elements and homogenization. International Journal of Solids and Structures. 2008. No. 45(20). pp. 5258–5288.
6. Зимин С. С., Беспалов В. В., Казимирова А. С. Расчетная модель каменной арочной конструкции // Вестник Донбасской национальной академии строительства и архитектуры. 2015. № 3(113). С. 33–37.
7. Беспалов В. В., Зимин С. С., Прочность каменной кладки сводчатых, Строительство уникальных зданий и сооружений, 2016, № 11 (50). С. 37–51.
8. Angelo Gaetani Seismic Performance of Masonry Cross Vaults: Learning from Historical Developments and Experimental Testing 2016
9. СП 15.13330.2012 «Каменные и армокаменные конструкции. Актуализированная редакция СНиП II-22-81*» (с Изменениями N 1, 2). 01.01.2013 и СП 70.13330.2012 «Несущие и ограждающие конструкции. Актуализированная редакция СНиП 3.03.01-87» (с Изменениями N 1, 3) 01.07.2013.
10. СП 15.13330.2012 «Каменные и армокаменные конструкции. Актуализированная редакция СНиП II-22-81*» (с Изменениями N 1, 2). 01.01.2013

Основные термины (генерируются автоматически): крестовый свод, свод, кирпичная кладка, конструкция, гомогенная модель, забутовка, конечно-элементное моделирование, расчет сводов, эпюр моментов, диагональное ребро.

Расчет и анализ сезонного хода температуры в контактной зоне облицовочного слоя и забутовки после восстановления ограждающей конструкции : научное издание

Тип публикации: статья из журнала

Год издания: 2020

Ключевые слова: envelope structures, heat loss, temperature gradient, deformation, facing verst, reinforcement, BRICK walls, ограждающие конструкции, теплопотери, градиент температуры, деформации, облицовочная верста, армирование, кирпичные стены

Аннотация: В статье проанализированы возможные дефекты наружных кирпичных стен зданий, построенных по технологии многослойной кладки; рассмотрены причины их возникновения и способы устранения дефектов. Научная работа построена на материалах обследования здания, расположенного в городе Абакан Республики Хакасия. В ходе сплошного визуального обследования выявлено, что участок облицовочной версты на южном фасаде площадью 25 м² получил деформации выпучивания. Вследствие чего произошло обрушение аварийного участка версты вследствие ее «отставания» от основной кладки стен. В рамках проведения обследования были выполнены работы по закреплению облицовочной версты -аварийное состояние конструкции устранено. В статье приведен расчет методом конечных элементов (МКЭ) в программных комплексах ElCUT и SCAD Office деформированной части наружной стены здания, подтверждающий причины образования дефектов кладки. Проведена тепловизионная съемка обследуемого здания с целью определения отрицательного влияния металлических анкеров на поверхность стены. Анализ полученных результатов расчета МКЭ в программном комплексе ElCUT свидетельствует о том, что наличие металлического анкера приводит к существенному изменению температуры и влажности. Результаты проведенного обследования позволяют нам сделать вывод, что проектирование ограждающих конструкций по существующим нормам не является безусловной гарантией их эксплуатационной надежности, а отсутствие на стадии проектирования моделирования стационарных и нестационарных тепло-влажностных процессов, протекающих в конструкциях во время эксплуатации с учётом климатических особенностей района строительства, приводит к уменьшению долговечности, увеличению теплопотерь и к преждевременному старению конструкций.
The article analyzes the possible defects of the external brick walls of buildings using multilayer masonry technology; the reasons for their occurrence and ways of eliminating defects are considered. The work is based on materials from a survey of a building located in the city of Abakan, Republic of Khakasia. In the course of a continuous visual examination, it was revealed that a section of the facing verst on the southern facade with an area of 25 m² received deformations. As a result, the emergency section of a mile collapsed due to its gap from the main masonry of the walls. As part of the study, work was carried out to secure the facing verst — the emergency state of the structure was eliminated. The article presents the calculation by the finite element method (FEM) in the software complexes ElCUT and SCAD Office of the deformed part of the outer wall of the building, confirming the reasons for the formation of masonry defects. A thermal imaging survey of the building under study was carried out in order to determine the negative effect of metal anchors on the wall surface. An analysis of the results obtained for calculating the FEM in the ElCUT software package indicates that the presence of a metal anchor leads to a significant change in temperature and humidity. The results of the study allow us to conclude that the design of enclosing structures according to existing standards is not an unconditional guarantee of their operational reliability, and the absence at the design stage of modeling stationary and non-stationary heat and humidity processes occurring in structures during operation, taking into account the climatic features of the construction area, leads to a decrease in durability, an increase in heat loss and premature aging of structures.

Ссылки на полный текст

Как оценить объем засыпки грязи | Руководства по дому

Автор: Дайана К. Уильямс Обновлено 17 декабря 2018 г.

При улучшении домашнего ландшафта вам может потребоваться засыпать участок грунтом. Определение правильной формулы объема для вашего проекта зависит от формы области, которая должна быть заполнена. Для области прямоугольной формы вы должны умножить три измерения. Круглые формы требуют, чтобы вы использовали геометрическое значение пи в своей формуле. Главное помнить, что все ваши измерения должны быть в одних и тех же единицах. Если вы берете свои измерения в дюймах, их будет легко преобразовать в кубические ярды, так как грязь продается в единицах объема.

Прямоугольная область

1. 1.

   Измерьте длину, ширину и глубину области, которую вы хотите заполнить землей. Запишите размеры в дюймах. Например, предположим, что длина составляет 10 футов (120 дюймов), ширина — 5 футов (60 дюймов), а глубина — 2 фута 6 дюймов (30 дюймов).

2. 2.

   Рассчитайте объем грязи, необходимый для заполнения измеренной площади, умножив длину (120 дюймов) на ширину (60 дюймов) на глубину (30 дюймов). Общий объем равен 216 000 кубических дюймов.

3. 3.

   Преобразование кубических дюймов в кубические ярды путем деления на 46 656 кубических дюймов. Итак, 216 000 кубических дюймов разделить на 46 656 кубических дюймов равно 4,63 кубических ярда. Чтобы заполнить прямоугольную область на глубине 2 фута 6 дюймов, вам понадобится 4,63 кубических ярда земли.

Площадь круга

1. 1.

   Измерьте диаметр и глубину отверстия, которое вы хотите заполнить землей. Запишите свои измерения в дюймах. Для этого примера предположим, что отверстие, которое вы засыпаете, имеет диаметр 5 футов (60 дюймов) и глубину 2 фута 6 дюймов (30 дюймов). Радиус 5 футов составляет 2,5 фута (30 дюймов).

2. 2.

   Рассчитайте объем земли, необходимый для заполнения ямы, используя пи (3,142), умноженное на квадрат радиуса, умноженный на глубину. В этом примере вы должны умножить 3,142 на квадрат 30 на 30, чтобы получить объем. Это дает 3,142 умножить на 900 дюймов и умножить на 30 дюймов, или 84 834 кубических дюйма.

3. 3.

   Преобразуйте 84 834 кубических дюйма в кубические ярды, разделив на 46 656 кубических дюймов. Чтобы заполнить яму, потребуется 1,82 кубических ярда земли.

   Вещи, которые вам понадобятся

   • Рулетка

   • Калькулятор

   Совет

   Если ваши измерения указаны в футах, вы можете преобразовать кубические футы в кубические ярды, разделив 7 на 2.

Справочные материалы

• School Improvement in Maryland: Справочник по формулам
• University of Nevada Cooperative Extension: Преобразование для общеупотребительных мер и весов
• Открытый справочник по математике: объем, заключенный в цилиндр
• Калькулятор заполнения грунта: калькулятор заполнения в форме цилиндра и имеет степень бакалавра наук в области биологии и экологических исследований Северного университета Огайо. Уильямс — победитель ежегодного писательского конкурса журнала Writer’s Digest.

  TecKnowledge: расчет земляных работ и обратной засыпки

  Расчет земляных работ и обратной засыпки не так прост, как получение объема грунта. Необходимо учитывать угол естественного откоса и уплотнение.

  A. Угол естественного откоса

  Угол естественного откоса представляет собой угол, который образует сыпучий материал от горизонтали, когда он свободно размещен на плоской поверхности. Поэтому при проведении земляных работ необходимо рассчитывать не только объем грунта непосредственно под заданным участком, но и прилегающую территорию по периметру, образующую пандусы из-за угла откоса разрыхленного после земляных работ грунта.

  Угол естественного откоса зависит от коэффициента внутреннего трения материалов. Вот примерные средние значения угла естественного откоса для конкретных типов материалов.

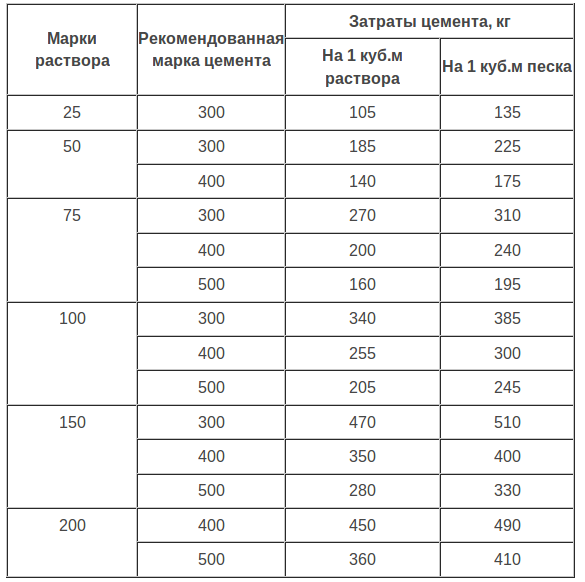
  Таблица 1 – Средний угол естественного откоса различных материалов

  Тип материала	Угол естественного откоса (градусы)
  Сухой песок	27,5
  Влажный песок	37,5
  Влажный песок	30
  Обыкновенная сухая земля	32,5
  Обыкновенная влажная земля	35
  Обыкновенная влажная земля	27,5
  Гравий	39
  Гравий, песок и глина	25

  Вы действительно можете измерить угол естественного откоса материала. Получите образец сыпучего материала. Налейте его на плоскую поверхность и измерьте угол, который он образует с горизонтом.

  Применяя закон касательных, мы можем рассчитать горизонтальное расстояние X, которое будет добавлено к вычислению объема.

  tanθ= ГЛУБИНА/x

  x= ГЛУБИНА/(tanθ)

  Пример:

  Рассчитайте общий объем грунта, который необходимо выкопать для котлована размером 10 м x 20 м и глубиной 2 м. Предположим, что почва обычная влажная.

  Дано:

  Глубина = 2m

  θ = 35 градусов для обычной влажной Земли

  Площадь = 10 м х 20 м

  Решение:

  x = глубина / tan θ

  = 2m / tan35

  x = 2,86 м.

  Базовый размер: 10 м на 20 м

  Верхний размер: (10 м+2x) на (20 м+2x)

  Базовая площадь = A1 = 10 x 20 = 200 м ²

  Верхняя площадь = A2 = (10+ 2*2,86) (20+2*2,86) = 404,3 м ²

  V = 2/3 (200+404,3+SQRT (200+404,3)

  V = 592,44 M ³

  B ³

  B.