Градиент фильтрации: градиент напора фильтрации | Перевод градиент напора фильтрации?

Содержание

8.Начальный градиент напора.

Многочисленные
опыты по фильтра­ции воды в песчаных
грунтах подтверждают полную справедливость
закона Дарси. Вместе с тем опыты с
пылевато-глинистыми грунтами показывают
систематическое отклонение от этого
закона.

Так,
в глинистых грунтах, особенно плот­ных,
при относительно небольших значениях
градиента напора фильтрации может не
возникать (начальный участок кривой).

Увеличение
градиента приводит к постепенному,
очень медленному развитию фильтрации.
Наконец, при некоторых значениях
гидравли­ческого градиента
устанавливается постоянный режим
фильтрации. Во многих случаях исключают
из рассмотрения начальный кри­волинейный
участок и закон ламинарной фильтрации
для пылевато-глинистых грунтов принимают
в виде.

Понятие
начального градиента напора впервые
установлено опытами Б. Ф. Рельтова и С.
А. Роза и связывается обычно с прояв­лением
особых свойств воды в глинистых грунтах,
отмеченных в начале настоящего параграфа.
С. А. Роза показал, что для плот­ных
кембрийских глин начальный градиент
напора может достигать очень больших
значений, порядка 10…20.

При
действующем градиенте напора меньше
начального значе­ния фильтрация в
водонасыщенном грунте практически не
возникает, а следовательно отсутствует
возможность уплотнения грунта.

При
расчетах осадок оснований мощность
зоны уплотнения иногда ограничивают
той глубиной, где выполняется условие

9.Эффективное и нейтральное давление в грунтовом массиве.

Механическая
модель (см. рис. 2.8) наглядно демонстрирует,
что в процессе уплотнения грунта в нем
одновременно действуют две системы
давлений: давление в скелете грунта,
называемое эффективным, и давление в
поровой воде, называемое нейтральным.
Эффективное давление характеризует
напряженное состояние скелета грунта.
Под этим давлением грунт уже деформировался,
т. е. уплотнился и упрочнился. Следовательно,
такое давление эффективно сказывается
на состоянии грунта. Нейтральное же
давление не влияет на напряженное
состояние скелета полностью водонасыщенного
грунта, т. е. оно нейтрально по отношению
к скелету грунта.
Обозначим эффективное
давление рd, а нейтральное давление pω.
Руководствуясь выражением (2.19) можно
записать
p = рd + pω

Отсюда
эффективное давление

рd
= p – pω

где
р — полное, или тотальное, давление,
действующее в грунте.

Эти
рассуждения справедливы только для
грунта, полностью насыщенного водой.
Если же поровая вода в грунте содержит
воздух в растворенном виде или в виде
пузырьков, то, как показали опыты,
проведенные в ЛИСИ, после приложения к
образцу грунта гидростатического
давления он получал деформации, так как
объем поровой воды, содержащей воздух,
уменьшился. В таком случае давление в
поровой воде нельзя считать нейтральным.
Однако и в этих опытах гидростатическое
давление передавалось частично на воду,
заключенную в порах, и частично на скелет
грунта.

10.Коэффициент бокового давления грунта. Модуль общей деформации.

Основными
характеристиками сжимаемости грунтов
являются модуль общей деформации Е или
коэффициент относительной сжимаемости
mv, коэффициент поперечного расширения
(коэффициент Пуассона) v и коэффициент
бокового давления ξ грунта.

Коэффициент
относительной сжимаемости

При
расчетах осадок уплотнения грунтов
вместо коэффициента сжимаемости
используется коэффициент относительной
сжимаемости (mv):

(5.10)

Коэффициент
бокового давления

Коэффициент
бокового давления (ξ). В состоянии покоя,
т.е. при отсутствии горизонтальных
перемещений, он представляет отношение
поперечных сжимающих напряжений к
продольным при ех=еу=0, т.е.

(5.17)

Коэффициент
поперечного расширения

Коэффициент
поперечного расширения (коэффициент
Пуассона) представляет отношение
поперечных деформаций — относительных
горизонтальных к относительным
вертикальным, т. е.

(5.20)

Модуль общей
деформации грунта

Модуль
общей деформации грунта используется
в качестве деформационного показателя
и характеризует упругие и остаточные
деформации. Модуль общей деформации
является важной характеристикой,
используемой для расчета оснований и
сооружений по деформациям. Модуль общей
деформации определяется в полевых и
лабораторных условиях. Наиболее
распространен способ проведения
компрессионных испытаний с последующей
их обработкой. В этом случае модуль
общей деформации

(5.24)

Гидравлический градиент, его размерность. Скорость фильтрации и скорость движения воды. Начальный градиент фильтрации

Другие предметы \
Механика грунтов

Страницы работы

1
страница
(Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

80. Одинаковы или различны
напоры в сосуде на поверхности воды и на дне сосуда? Одинаковы или различны
давления в воде в этих точках? напоры в сосуде на поверхности
воды и на дне сосуда различны также как и давления в этих точках.

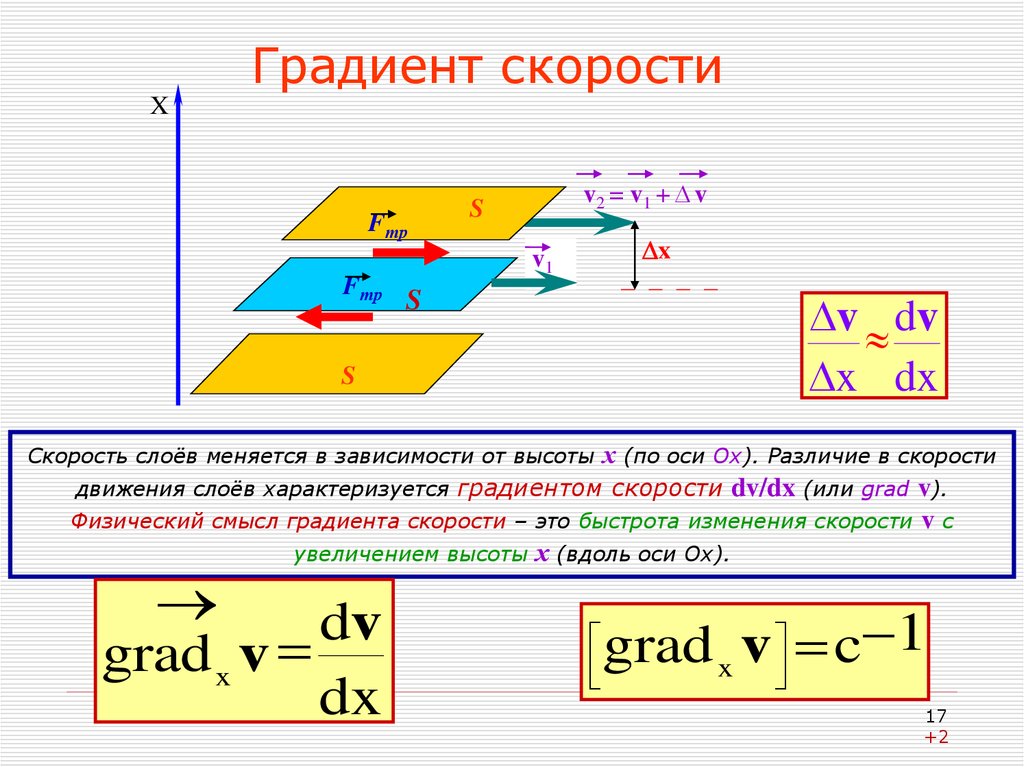
81.Что такое гидравлический
градиент? Какова его размерность?

гидравлический градиент-потеря
напора отнесенная к длинна фильтрации. Безразмерная величина.

82.Запишите закон Дарси.
Какова размерность коэффициента фильтрации? От чего он зависит?

закон Дарси (ламинарной
фильтрации)-скорость фильтрации прямопропорциональна гидравлическому
градиенту.Коэффициент фильтрации измеряется в сантиметрах в секунду,зависит от гранулометрического
состава и плотности грунта.

83.Что такое скорость
фильтрации и скорость движения воды?

скорость фильтрации-объем
воды, проходящий за единицу времени через единицу площади поперечного сечения
грунта.Скорость движения воды-скорость с которой вода
течет в свободном состоянии.

84.Что такое начальный
градиент фильтрации?

фильтрация воды начинается
лишь при градиенте большем некоторого значения,необходимого для преодоления
сопротивления ее движению водно-коллоидных пленок.это значение и есть начальный
градиент.

85.Что называется
гидродинамическим давлением и какова его размерность?

гидродинамическое
давление

86.Опишите модель водонасыщенного грунта К. Терцаги.

В стакан 1 поставим пружину 5 и до ее верха
нальем практически не сжимаемую (не содержащую воздуха) воду 4.На поверхность
воды и верх пружины поставим поршень 2 с отверстием малого диаметра и
приложим к поршню нагрузку 3,создающую внешнее давление р.В первый
момент времени (при t = 0),пока вода не успела выйти из
отверстия,поршень еще не переместился по вертикали,следовательно, пружина не
получила деформацию и усилие в ней рz = 0.в воде же возникнет давление рw =р. Значит,в первый момент времени давление полностью передается на
воду.По мере выдавливания воды из стакана через отверстие, поршень будет
опускаться.Это приведет к сжатию пружины и увеличению в ней напряжений.В
течение этого процесса значение pwуменьшается,а рzувеличивается и будет сохраняться равенство

После выдавливания определенного количества
воды давление р будет полностью передано на пружину, т.е. при t стремящемся к бесконечности давление pw= 0

Механическая модель в какой-то степени
иллюстрирует деформацию полностью насыщенного водой грунта, не обладающего
структурной прочностью, ползучестью скелета и начальным градиентом напора. В
образце водонасыщенного грунта, помещенного в одометр, при приложении
нагрузки в поровой воде возникает давление pw. По мере выдавливания воды из образца давление в поровой воде уменьшается,
а давление в скелете грунта увеличивается.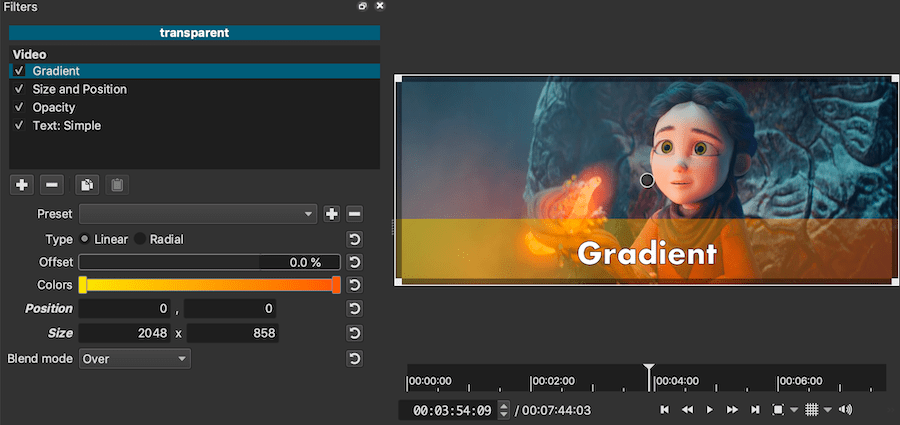 Следовательно, давление в пружине
моделирует давление в скелете грунта, а давление в воде соответствует давлению
в поровой воде.

87.Что такое полное, эффективное и нейтральное
давления?

в процессе уплотнения грунта в нем
одновременно действуют две системы давлений: давление в скелете грунта,
называемое эффективным, и давление в поровой воде, называемое нейтральным.
Эффективное давление характеризует напряженное состояние скелета грунта.Под
этим давлением грунт уже деформировался,т. е. уплотнился и упрочнился.
Следовательно, такое давление эффективно сказывается на состоянии грунта.Нейтральное
же давление не влияет па напряженное состояние скелета полностью водонасыщенного
грунта,т. е. оно нейтрально по отношению к скелету грунта.

88.Что
называется гидростатическим и поровым давлением?

Поровое давление(нейтральное)-давление в
поровой воде,гидростатическое
давление89.Дайте
понятие о прочности грунта.

Прочность грунта-способность грунта
сопротивляться разрушению.обеспечивается связями между частицами грунта.

90.Чем
вызывается сопротивление грунта сдвигу?

Трение возникающее в точках контактах
частиц.

91.Назовите
методы определения сопротивления грунта сдвигу.

Сопротивление грунта сдвигу может быть
установлено испытанием его образцов на сдвиг,путём трёхосного сжатия,вдавливанием
штампа с шаровой или конусообразной поверхности, по результатом среза грунта
крыльчаткой по цилиндрической поверхности и др.

92.Начертите
принципиальную схему прибора для испытания грунтов

Похожие материалы

Информация о работе

Скачать файл

[CV] 3. Градиентный и лапласовский фильтр, разность гауссианов (DOG) | от jun94 | jun-devpBlog

Ранее мы рассмотрели фильтры, используемые для сглаживания или удаления шума на изображениях. В этой главе будут объяснены фильтры, которые должны извлекать информацию о границах изображений.

Прежде чем мы начнем, обратите внимание, что фильтры можно рассматривать как шаблоны . Это означает, что применение фильтра в какой-то момент можно рассматривать как скалярное произведение между одномерным представлением области изображения и одномерным векторным представлением фильтра. Таким образом, отклик фильтра максимален, когда область, в которой применяется фильтр, выглядит так же, как и фильтр. Другими словами, фильтры выглядят как эффекты (или функции изображения), для поиска которых они предназначены. 1.1 Градиент изображения общий выбор, чтобы найти края. Тогда что делает градиент облегчающим обнаружение краев и почему он полезен?

На это можно ответить с помощью следующего примера на рис. 2. Левая панель — это данное изображение, а панель в центре — соответствующие интенсивности пикселей для пикселей на красной строке изображения. Как видно из двух панелей, края изображения — это места, где интенсивность пикселей сильно меняется, например, от белого к черному и от черного к белому.

Рисунок 2. График интенсивности пикселей и 1-й производной заданного изображения из [1]

Учитывая определение краев, в рассмотрение вступает идея градиента, поскольку области без краев возвращают нулевой градиент, в то время как другие области выводят некоторые положительные или отрицательные значения. Это показано на правой панели рис. 2. Карта 1-й производной показывает ненулевую реакцию только в пикселях, где лежат края. Таким образом, мы можем заключить, что, находя пиксели, являющиеся результатом максимумов 1-й производной, можно определить границы изображения.

1.2 Разработка фильтра для вычисления производных

Чтобы вычислить производную изображения, мы можем использовать концепцию свертки с фильтром (обратите внимание, что ее также можно вычислить путем корреляции). Вспомним, как вычисляется частная производная в функции 2D f , представляющей изображение. В непрерывной настройке частная производная от f по отношению к x определяется следующим образом:

Уравнение 1. Частная производная от f по x

Однако в компьютерном зрении мы имеем дело с изображениями, которые представляют собой дискретные данные. Таким образом, мы аппроксимируем его, используя конечные разности.

Уравнение 2. Дискретизированное уравнение 1.

Для реализации уравнения 2 в виде свертки соответствующий фильтр будет

Рисунок 3. Сверточный фильтр для вычисления градиента изображения из [2] производная от f по отношению к y . На рис. 4 показан отклик фильтра после свертки по отношению к x (в центре) и y (правая панель).

Рисунок 4. Карты отклика фильтра (центральная и правая панель) после свертки с фильтрами x-gradient и y-gradient соответственно из [1], [2]

известно, что на практике мы используем градиентный фильтр 3 × 1 для x Производная вместо градиентного фильтра 2 × 1 , а также для y Производная ( 1 × 3 фильтр). Позвольте мне объяснить, почему и как построить фильтр 3 × 1 (для производных по отношению к x ).

Несмотря на простоту фильтра: [1 -1], у него есть некоторые проблемы.

  • Во-первых, после свертки изображения с помощью этого фильтра он сдвигает изображение на полпикселя.
  • Во-вторых, что также связано с первой причиной, когда мы применяем [1 -1] к 2 пикселям (x, y) и (x+1, y) , фактически вычисляется градиент в позиции (x+0.5, y) не в позиции (x, y) и (x+1, y) . Чтобы исправить это, мы вставляем 0 между [1 -1] , чтобы получить [1 0 -1] . Путем свертки нового фильтра [1 0 -1] с пикселями (x -1, y), (x, y) и (x+1, y) , он возвращает градиент относительно x для центрального пикселя (x, y) .

Вкратце,

  • фильтр производной x: [1 -1] -> [1 0 -1]
  • фильтр производной y: [1 -1] ᵀ -> [1 0 -1] ᵀ

более подробное объяснение см. в [8]. Если мы напрямую вычисляем производные изображения, содержащего шум, то это дает неожиданный результат, когда мы не можем обнаружить никакой информации о расположении краев. Рис. 5 иллюстрирует это.

Рис. 5. Вычисленные производные зашумленного изображения из [1], [3]

Рассмотрим одну строку изображения (вспомним красную линию на рис. 2) и нанесем на график интенсивности f пикселей на ряд, как показано ниже. Поскольку из-за шума интенсивность каждого пикселя колеблется по сравнению с другими, при вычислении их производных мы получим только зигзагообразные узоры. Таким образом, чтобы правильно выделить местоположения краев, удаление шума должно предшествовать вычислению производных изображений.

И мы уже знаем, как исключить шум, Фильтрацию по Гауссу (Сглаживание).

Рис. 6. Правильный подход к обнаружению краев на зашумленном изображении с помощью фильтров Гаусса и производных, из [1], [3]

Сначала сверните изображение с помощью фильтра Гаусса с определенной сигмой (стандартным отклонением).

После этого мы получаем изображение, из которого до определенной степени удалены шумы.

Затем, вычислив производную изображения и взглянув на его пик, мы получим расположение краев.

1.4 Как сделать этот процесс эффективным? (Производная от Гаусса)

Пусть f и h будут изображением и фильтром соответственно. Одной из характеристик свертки является то, что производная свернутого изображения (h ⋆ f) эквивалентна свернутому изображению f с дифференцированным фильтром ∇ h .

Используя это, мы можем упростить шаги на рис. 6. На этот раз мы сначала вычисляем дифференцированный фильтр ∇ h и свернем его с изображением f.

Это дает тот же результат, что и на рис. 6.

Рис. 7. упрощенный подход к поиску краев на изображении, из [1], [3]

Наконец, напомним, что мы можем представить вычисление производной в виде свертки с фильтр [1 -1] (или [1 0 -1] , как указано выше). Следовательно, производная члена фильтра ∇ h становится сверткой [1 -1] и фильтр Гаусса h, , как показано ниже.

И результат этой свертки (Производный фильтр ⋆ h ) называется Производной Гаусса.

Короче говоря, фильтр Gaussian Derivative содержит как гауссовское сглаживание, так и вычисление производной. Следовательно, пока мы сворачиваем изображение с фильтром Производная Гаусса , нет необходимости отдельно выполнять сглаживание Гаусса и вычисление производной, как показано на рис. 6.9.0004 Пример производной фильтра Гаусса по направлениям x и y

Фильтр Лапласа — это один из детекторов границ, используемый для вычисления вторых пространственных производных изображения. Он измеряет скорость изменения первых производных. Другими словами, фильтр Лапласа выделяет области, в которых интенсивность пикселей резко меняется. Из-за этой характеристики фильтра Лапласа его часто используют для обнаружения краев изображения. Позже мы увидим, как фильтр находит края с помощью визуальной иллюстрации.

Математическое определение лапласиана следующее.

Учитывая определение, дискретизированный 3 x 3 Фильтр Лапласа (поскольку мы имеем дело с изображениями, и они дискретны) для изображения f определяется как массив ниже:

Рисунок 8. Лапласиан 3 x 3 filter

Обратите внимание, что указанное выше ядро, которое не идентично математическому определению лапласиана из-за противоположных знаков, использует отрицательный пик, поскольку оно более распространено и прямолинейно. Тем не менее, он по-прежнему действителен.

2.1. Обнаружение края

Давайте вернемся к причине, по которой мы используем фильтр Лапласа. Как упоминалось ранее, фильтр Лапласа является одним из распространенных методов обнаружения края, но как?

Рисунок 9. пример отсюда

Сначала мы вычисляем вторую производную для каждого пикселя. Наша цель — найти краевые местоположения (пиксели), и ранее мы находили их, глядя на максимумы первых производных. Вспомните, как мы нашли максимумы первых производных со второй производной. Ответ таков: края находятся между пикселями, вторые производные которых резко переходят от одного знака к другому (пересечение нуля). Два обнаруженных ребра среди всех ребер отмечены сине-зеленой рамкой на рис. 9..

2.2. Лапласиан Гаусса

Подобно 1.4 Производная Гаусса, применяется та же идея для упрощения обнаружения границ с помощью фильтра Лапласа. В то время как все остальные шаги остаются прежними, единственное отличие от Производная фильтра Гаусса заключается в том, что фильтр Лапласа заменяет фильтр производной, что означает, что ∇ h на рис.

Рис. 10. Правильный подход к обнаружению краев на зашумленном изображении с помощью фильтров Гаусса и Лапласа, из [1], [3]

Поскольку лапласиан (∇²) также может быть представлен сверткой с фильтром Лапласа, мы свернем фильтр Лапласа с фильтром Гаусса, и, следовательно, мы получим фильтр Лапласиана Гаусса (LoG) . Подобно Производная Гаусса , LoG содержит сглаживание по Гауссу и вычисление второй производной, нет необходимости проводить их отдельно, пока изображение свертывается с Логом .

Рис. 11. Иллюстрация построения фильтра LoG для облегчения понимания, из [1], [7]

Обратите внимание, что размер фильтра и значения на рис. 11 выбраны произвольно, поэтому вычисленный LoG не точен. Рассмотрим это в качестве примера, чтобы просто увидеть общую картину того, как фильтр LoG структурирован с использованием свертки.

Различие гауссиан и результирующего изображения после свертки по ним показано ниже.

Рис. 12. Лапласиан ~ Отличие гауссиана, из [1]

Заметным наблюдением здесь является то, что вычитание одного гауссиана другим приближается к лапласиану гауссиана. Это указывает на то, что при аппроксимации LoG фактическое вычисление производной не требуется. Еще одна причина, по которой DoG полезен, заключается в том, что в задачах компьютерного зрения изображение часто фильтруется фильтрами Гаусса во многих масштабах. Сохраняя результаты гауссовской фильтрации изображения, мы можем легко использовать их для извлечения краев путем вычисления разницы между последующими выходными данными фильтрации без фактического вычисления производных изображений.

[1] RWTH Aachen, группа компьютерного зрения

[2] CS 376: Computer Vision of Prof. 5] Проф. Светлана Лазебник

[6] Проф. М. Ирани и Р. Басри

не [-1 1]?

Приветствуются любые исправления, предложения и замечания

Как использовать градиентный фильтр для улучшения фотографий

Инструмент градиентного фильтра обычно используется для затемнения или осветления верхней части фотографии — неба. По сути, он заменяет физический градуированный фильтр, который вы надеваете на объектив камеры. В Zoner Photo Studio X вы можете настроить параметры, предоставляя вам множество творческих возможностей.

Помимо градуированных фильтров, о которых вы можете прочитать в статье Градуированные фильтры, вы также можете использовать «виртуальный» фильтр. Это инструмент Zoner Photo Studio в версии 9.0007 Разработать модуль . Вы также можете использовать градиентный фильтр для неразрушающего редактирования и при редактировании изображений RAW.

Изменение настроек

Сначала выберите инструмент Gradient Filter (G). Если вы хотите отредактировать небо в верхней части фотографии, вы можете сделать это, щелкнув и перетащив вверх. В зависимости от размера фильтра градиент будет более или менее плавным. Вы можете точно настроить этот переход, используя параметр Широкий градиент .

СОВЕТ : Иногда может понадобиться использовать функцию Инвертировать маску , которая перевернет весь фильтр. Вы найдете эту опцию на правой панели с опциями для отдельных масок.

Выберите градиентный фильтр (G) и отредактируйте только часть фотографии.

Градиентный фильтр имеет множество настроек, которые вы можете настроить. Это означает, что вы можете не только осветлять или затемнять часть фотографии, но также можете добавлять контраст, повышать резкость, настраивать светлые или темные тона или работать с локальной цветокоррекцией и кривыми. У вас также есть возможность установить оттенки для определенного цвета.

Локальная цветокоррекция 

С помощью градиентного фильтра вы также можете локально работать с цветами. Используйте локальные кривые Цветовая коррекция и Тональная для настройки контраста в дополнение к цвету. Эта коррекция сослужит вам хорошую службу при редактировании пейзажных фотографий и изменении цветов неба.

С помощью кривых RGB или Luma можно точно настроить локальный контраст и кривые для отдельных цветовых каналов , внесение основных изменений в цвет. Если вас интересует тонирование с помощью кривых, мы написали статью о том, как тонировать цвета с помощью кривых.

Вы можете локально редактировать контраст и цвет с помощью тоновых кривых.

Если вы хотите еще больше отредактировать свои цвета, используйте Color Shift. С помощью Color Shift вы можете изменить оттенок, насыщенность и яркость любого цвета, выбранного на фотографии. На этой конкретной фотографии цвет неба мне показался неправильным, поэтому с помощью пипетки я выделил его и придал более темные, сине-фиолетовые оттенки.

Отрегулируйте цветовые оттенки, используя локальную коррекцию цвета.

Создаем правильную атмосферу для вечерних облаков

Вечернее небо часто окрашивается в интересные оттенки. Вы можете передать это ощущение с помощью градиентного фильтра и сделать цвета более яркими с помощью насыщенности и контрастности.

Раскрашивание неба.

Выделение звезд

Четкость и Резкость настройки помогут вам выделить звездное небо. Эти настройки доступны в Zoner Photo Studio X отдельно от Градиентного фильтра. Однако, если вам нужно выделить только часть фотографии, например, только звезды, лучше всего подойдет Градиентный фильтр.

Подсветка звезд.

Улучшение фотографий с рамкой солнце/тень

В летнее время часть снимка часто попадает под прямые солнечные лучи, а остальная часть находится в тени. Это создает впечатление, что одна часть изображения переэкспонирована, а другая недоэкспонирована. Если есть сплошная линия, разделяющая две части, вы можете использовать градиентный фильтр.

Затемнение более светлой верхней части фотографии.

Использование нескольких фильтров одновременно

На этой фотографии нам нужно немного затемнить небо. Нажав Добавить маску , можно применить сразу несколько фильтров. Второй фильтр затемнит только небольшую верхнюю часть неба. Вы можете проверить список всех фильтров, используемых в таблице выше.

Два градиентных фильтра на одной фотографии.

Подкрашивание только части фотографии 

Другой вариант использования градиентного фильтра – использование карты градиента для окрашивания части фотографии. Все зависит от ваших творческих предпочтений. Используйте настройку Color , которую вы найдете в нижней части настройки Gradient Filter. Например, вы получите захватывающие винтажные цвета, используя оттенки фиолетового в Режим исключения .