Газоблок теплопроводность характеристики: Теплопроводность газобетона

Содержание

Теплопроводность газобетона — АлтайСтройМаш

В условиях постоянного роста количества населения все больше внимания уделяется совершенствованию технологий строительства. Газобетонные блоки отличаются внушительными габаритами, легким монтажом и улучшенными техническими характеристиками. Например, теплопроводность газоблока значительно ниже, чем у кирпича. Это делает материал экономичным при покупке и возведении зданий любого типа за счет сокращения количества сырья при сохранении должного уровня теплопроводности.

Алтайский завод строительного машиностроения проектирует и производит оборудование для производства газобетонных блоков. Станки собираются в России, поставляются на территорию Казахстана, Узбекистана, а также в любую другую точку мира. Помимо того, что газоблок способствует оперативному сооружению зданий, он долговечен, способен переносить до 150 циклов заморозки и разморозки.

Коэффициент теплопроводности газобетона по марке

На производственных линиях компании АлтайСтройМаш выпускаются газоблоки любых марок: D400, D500, D600 и т. д. Каждая марка газобетонных блоков служит определенной цели в работах по возведению зданий:

D400 применяется для строительства временных малогабаритных построек жилого типа. Сырье требует дополнительной отделки или облицовки. Цифра «400» говорит о том, что в 1 куб.м. газобетона содержится 400 кг твердого материала; остальное пространство занимают пузырьки воздуха.

D500 подходит для построек бытового и сельскохозяйственного назначения. Блоки немного прочнее, чем марка D400, однако еще не способны выдерживать нагрузку тяжелой кровли.

Блоки D600 и выше применяются при малоэтажном строительстве, обычно при возведении частных одноуровневых домов.

Пористая структура газобетонных блоков препятствует выдуванию тепла из внутренней части здания. Это позволяет экономить на теплоизоляционных материалах при дальнейших отделочных работах.

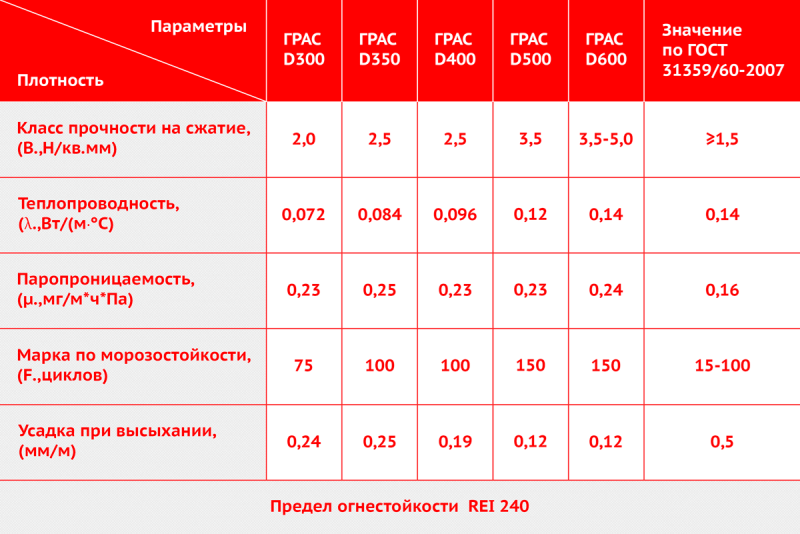
Таблица теплопроводности газобетона

Уровень влажности, %

Марка D400

Марка D500

Марка D600

0.096

0.112

0.141

0.117

0.147

0. 183

Коэффициент теплопроводности измеряется в Вт/м*°С. Приведенные характеристики отражают низкий уровень выдувания тепла. Показатель достигается ввиду того фактора, что пузырьки воздуха, находящиеся внутри блока, медленно меняют свою температуру.

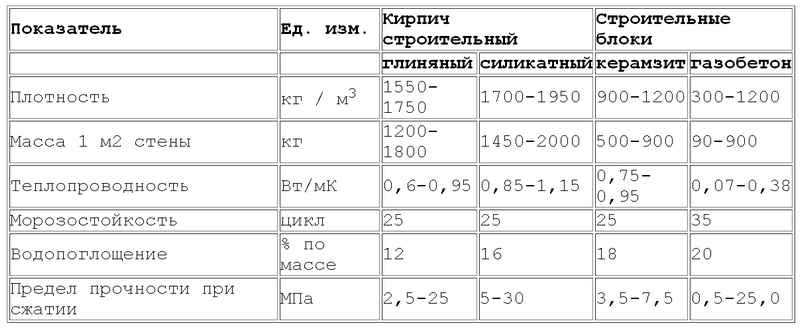
Теплопроводность газобетона: сравнение с деревом и кирпичом

Средневзвешенные показатели теплопроводности для газоблоков составляют 0,08-0,14 Вт/м*°С.

Для декоративного керамического кирпича, который используется при внешней облицовке стен здания, уровень теплоотдачи указывается в диапазоне от 0,36 до 0,42 Вт/м*°С.

Стены из обычного глиняного кирпича, уложенного в один ряд, соответствуют показателю 0,56 Вт/м*°С.

Самый дорогой силикатный кирпич также служит декоративным целям и не сохраняет тепло в здании из-за показателя в 0,71 Вт/м*°С.

Теплопроводность древесины зависит от сорта дерева и влажности окружающей среды. Ее характеристики находятся в диапазоне от 0,09 до 0,218 Вт/м*°С.

При просмотре нашего каталога товаров вы найдете объекты строительного машиностроения для производства блоков из газобетона. Материал для возведения и облицовки стен обладает хорошими перспективами и будет распространяться на новые сферы промышленности.

от чего зависит и какой коэффициент

Содержание

1 Что такое теплопроводность?
2 Зависимость от плотности
3 Зависимость от влажности
4 Зависимость от качества макроструктуры
5 Коэффициент теплопроводности марки D500
6 Коэффициент теплопроводности марки D600
7 Заключение

Индустрия строительства сегодня обеспечена многочисленными высокотехнологичными материалами, имеющими выдающиеся свойства. Одним из них является ячеистый бетон. Одна из разновидностей — газобетон. Производители гарантируют материалу высокие эксплуатационные характеристики. Например, обеспечивать сбережение комфортного внутреннего теплового режима зданий или передачу лишнего тепла за его пределы. Постоянное удорожание энергоресурсов делает все более актуальным фактором строительства снижение теплопроводности материалов.

Что такое теплопроводность?

Стены зданий предназначены стабилизировать комфортную температуру внутри помещений. Высокая теплопроводность стен холодной порой года будет быстро передавать тепло отопления наружу. Стоимость потребленных энергоресурсов вырастет, однако, жилое строение будет по-прежнему холодным. По этой же причине жаркие дни станут причиной внешнего нагрева стен. Материал передаст тепло внутрь строения, потребовав непременного охлаждения воздуха. Газобетону присущи иные свойства.

Само название подтверждает, что объем материала равномерно заполнен порами. Примерно 85% тела блоков — пустоты. Они заполнены воздухом, именно поэтому изделия имеют незначительный вес. По этому параметру продукция объединяет качества дерева, камня. Как известно «запертый» воздух является плохим проводником тепла. Значит, структура материала обладает ярко выраженной низкой теплопроводностью.

Показатель имеет наименьшую величину среди используемых стеновых материалов. Термин “теплопроводность” определяет способность передавать тепло внутри материала от одной более нагретой части объема к другой менее нагретой за счет теплового движение молекул. Измерение производится в Вт/(м °С). Показатель имеет название — коэффициент теплопроводности.

Фактически речь идет о количестве теплоты, которая передается через грань образца объемом 1 м. куб. за установленное время (например, 1 час) при формировании разности температур в 1 градус на противоположных сторонах. Технология изготовления газобетона задает макроструктурное качество, характеристики плотности, влажности материала. Именно от этих параметров зависит теплопроводность продукции.

Вернуться к оглавлению

Зависимость от плотности

Влияние плотности на теплопроводность.

Теплопроводность изделий формируется плотностью их материала. Чем они плотнее, тем быстрее передают холод (тепло) через свой объем. Стены из разных материалов, которые одинаково препятствуют теплопотерям, имеют разную толщину. Для сравнения: стены кирпичная шириной 210 см, из блоков газобетона сечением 44 см, из листов пенополистирола толщиной 12 см имеют практически равные показатели теплопропускания.

Сравнение стандартных величин теплопроводности кирпича — 0,35 Вт/(м °С) с газобетоном марки D400 — 0,10 Вт/(м °С) показывают, что условная кирпичная стена выпускает тепло из постройки быстрее, примерно от 3 до 4 раз. Одна из особенностей газоблоков в том, чем большую плотность он имеет, тем быстрее сооружение охлаждается. Есть обратная связь. Важно выдержать оптимум при выборе марки блоков, чтобы дом стал долговечным, теплым.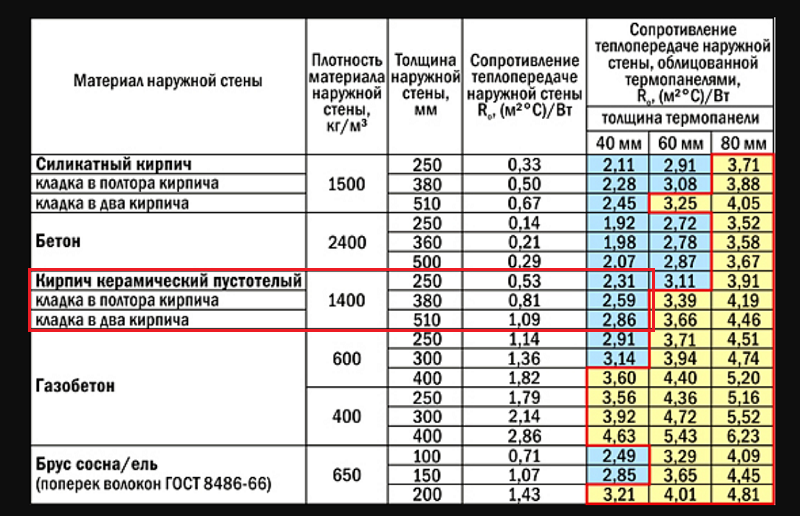

Вернуться к оглавлению

Зависимость от влажности

Влияние влажности на теплопроводность газобетона.

Формирование из блоков наружных стен сооружений предполагает взаимодействие, в первую очередь, с переменчивой влажностью окружающей среды. Хотя гигроскопичность материала достаточно низкая, однако, его структура все же подвержена впитыванию влаги. Реальные теплоизоляционные свойства изделий становятся несколько ниже, чем в стандартных условиях измерений. Величина равновесной эксплуатационной влажности наружных газобетонных стен может составлять до 10%. Поэтому, например, стандартный коэффициент теплопроводности, равный 0,12 Вт/(м °С) для блоков марки D500 в стандартных условиях, отличается от величины в условиях эксплуатационной влажности на 0,2 Вт/(м °С) и больше. Однако, это не много по сравнению, к примеру, с пустотелым строительным кирпичом, для которого в аналогичных условиях величина данного показателя ухудшается на 70-90%.

Вернуться к оглавлению

Зависимость от качества макроструктуры

Данная разновидность блоков отличается от пенобетонных тем, что содержит характерные вытянутые пустоты неправильной формы.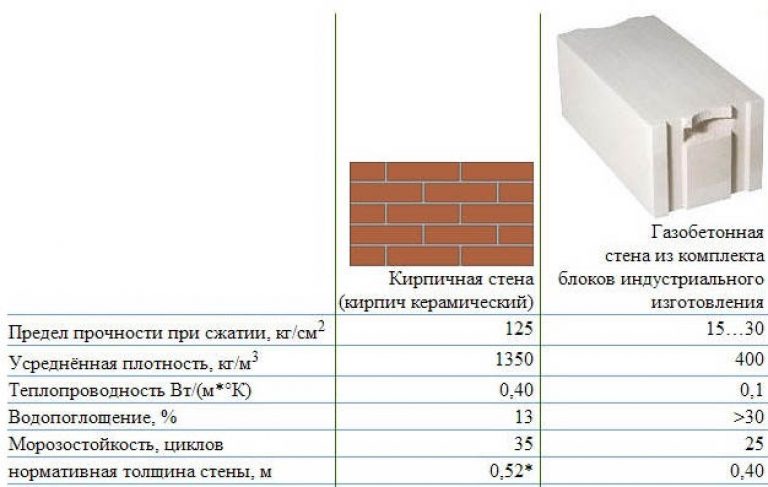 Такому образованию их формы материал обязан выходу газа в процессе отвердения. Газ выходит через образовавшиеся в порах трещинки, а значит, есть обратная сторона вопроса — подверженность продукции поглощению влаги.

Структуризацию материала определяют технологии изготовления. Определяющим фактором являются размеры внутренних пустот. Теплосберегающие свойства материала тем выше, чем больше пустотелых сфер в материале, а также чем меньших они размеров.

Вернуться к оглавлению

Коэффициент теплопроводности марки D500

Газоблоки данной марки классифицируются как конструкционно-теплоизоляционный материал. Величина показателя продукции в среднем равна 0,12 Вт/(м °С). Теплоизоляционные свойства стен, состоящих из уложенных блоков, могут достигать до 0,28 Вт/(м °С), что уже приближает их к кирпичу. Вместе с тем в соответствии с современными строительными нормами (к примеру, СТО 501-52-01-2007, ГОСТ 31360-2007 для РФ) газоблоки марок от D500 и выше могут быть использованы для кладки самонесущих стен высотой более 3-х этажей.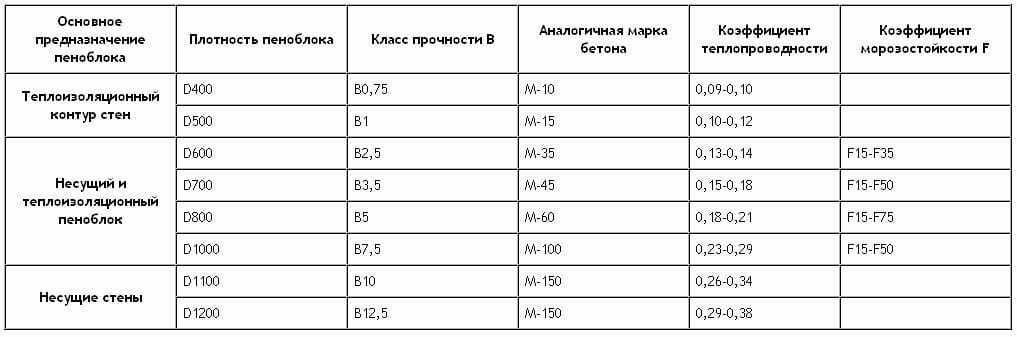

Вернуться к оглавлению

Коэффициент теплопроводности марки D600

Дом из газобетонных блоков сохраняет комфортную температуру в помещениях, как в зимний, так и в летнее время.

Данные изделия также являются конструкционно-теплоизоляционными. Средняя величина показателя для продукции составляет около 0,14 Вт/(м °С). Расчетные теплоизоляционные характеристики стен, состоящих из изделий марки D600, могут достигать до 0,31 Вт/(м °С). Для минимизации теплопотерь требуется точное выполнение рекомендаций по гидроизоляции материала от влаги воздуха, атмосферных осадков.

К сожалению, не только газоблоки составляют тело стен. Мостики передачи тепла создаются армопоясами, бетонными перемычками (поясами), кладочными швами. Последние резко понижают теплоизоляционные качества конструкции стен в целом.

Использование при монтаже специальных клеев снижает теплопроводность стен по сравнению с кладкой на цементные растворы. Вместе с тем повышение точности изготовления единиц продукции при одновременном увеличении их стандартных размеров позволяет сократить количество мостиков холода.

Вернуться к оглавлению

Заключение

За газобетоном настоящее и будущее жилищного строительства ввиду совершенствования норм, требований теплосбережения, роста цен на энергоносители. Простота возведения стен, отсутствие необходимости проводить дополнительное утепление, малые значения теплопроводности автоклавного газобетона позволяют существенно удешевить конструкцию сооружений.

Однако специфика строения пустот в газоблоках способствует впитыванию материалом влаги, поэтому их гидроизоляция обязательна. Конкретная климатическая зона строительства формирует индивидуальный подход как к выбору марки газоблоков, расчету толщины стен зданий, так и определяет их реальную теплопроводность.

Теплопроводность газов — tec-science

Теплопроводность идеальных газов не зависит от давления для не слишком сильно разбавленных газов. Это уже не относится к газам с низким давлением.

1 Введение
2 Зависимость теплопроводности от давления при высоких давлениях (плотные газы)
3 Зависимость теплопроводности от давления при низких давлениях (разбавленные газы)
4 Число Кнудсена

Введение

В статье Теплопроводность твердых тел и идеальных газов получена следующая формула для оценки теплопроводности λ идеальных газов:

\begin{align}
\label{l}
& \boxed{\ lambda = \frac{1}{3} \cdot c_v \cdot \rho \cdot v \cdot l} \\[5px]
\end{align}

В этой формуле c _v обозначает удельную теплоемкость при постоянный объем, ϱ плотность газа, v средняя скорость молекул газа и l длина свободного пробега. Эта формула будет объяснена более подробно в этой статье, и будут обсуждаться полученные выводы для газов.

Рисунок: Длина свободного пробега в разреженном газе с низким давлением и плотном газе с высоким давлением

Используя формулу, можно было предположить, что теплопроводность зависит от давления, так как чем выше давление, тем выше плотность газа . Этот аргумент также можно ясно понять с помощью корпускулярной модели материи, потому что чем больше частиц, тем больше энергии частицы могут переносить в сумме. Отметим, что согласно кинетической теории газов каждая молекула газа несет энергию ½⋅k _B ⋅T на степень свободы (с k _B в качестве постоянной Больцмана ).

Однако в той же мере, в какой плотность увеличивается с увеличением давления, длина свободного пробега уменьшается! Фактически, теплопроводность идеальных газов поэтому не зависит от давления или плотности частиц (для ограничения этого утверждения позже)!

Теплопроводность газов не зависит от давления при не слишком низком давлении!

Рисунок: Длина свободного пробега и средняя скорость молекул в газе

Независимость теплопроводности от давления для высоких давлений (плотные газы)

Независимость теплопроводности от давления также можно показать математически. Для этого плотность ϱ в уравнении (\ref{l}) сначала выражается как частное массы газа m _газа и объема газа V _газа . Тогда масса газа может быть выражена количеством вещества n _газа ( химическое количество ) и молярной массой M _газа газа.

\begin{align}
\lambda &= \frac{1}{3} \cdot c_v \cdot \frac{m_{gas}}{V_{gas}} \cdot v \cdot l \\[5px]
&= \frac{1}{3} \cdot c_v \cdot \frac{n_{gas} \cdot M_{gas}}{V} \cdot v \cdot l \\[5px]
\end{align}

Произведение удельной теплоемкости на молярную массу равно так называемой молярной теплоемкости C _m,v , при этом молярная теплоемкость зависит только от степеней свободы f и молярной газовой постоянной R _м (C _{м, v} = f/2⋅R _м ). Кроме того, количество вещества n _газа можно выразить отношением числа частиц N и постоянной Авогадро N _A (n _газа =N/N _A ):

\begin{align }
\lambda &= \frac{1}{3} \cdot \underbrace{c_v \cdot M_{gas}}_{C_{m,v}} \cdot \frac{n_{gas}}{V} \ cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \underbrace {C_{m,v}}_{=\frac{f}{2}R_m} \cdot \frac {N}{N_A \cdot V} \cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \frac{f}{2} R_{m} \cdot \frac{1}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
& = \frac{f}{6} \frac{R_m}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
\end{ align}

Отношение числа частиц к объему газа соответствует плотности частиц n, а частное молярной газовой постоянной и постоянной Авогадро соответствует постоянной Больцмана k _B (об этом соотношении см. статью Внутренняя энергия и теплоемкость):

\begin{align}
\lambda & = \frac{f}{6} \underbrace{\frac{R_m}{N_A}}_{k_B} \cdot \underbrace{\frac{N}{V}} _{n} \cdot v \cdot l \\[5px]
\label{ll}
& = \frac{f}{6} k_B \cdot n \cdot v \cdot l \\[5px]
\end {align}

Теперь нам нужны только зависимости средней скорости и длины свободного пробега. Согласно распределению Максвелла-Больцмана средняя скорость v молекул газа зависит от температуры газа T и массы молекулы m (m обозначает массу отдельной частицы газа, а не всей массы газа!)93 м }}} \\[5px]
\end{align}

Теперь эта формула ясно показывает, что теплопроводность идеальных газов не зависит от плотности частиц и, следовательно, не зависит от давления. Это также показывает, что газы с относительно большими молекулами имеют более низкую теплопроводность, чем газы с меньшими молекулами (это связано с уменьшением длины свободного пробега в результате большего диаметра столкновения d). Кроме того, теплопроводность газов с легкими частицами выше, чем у газов с более тяжелыми частицами.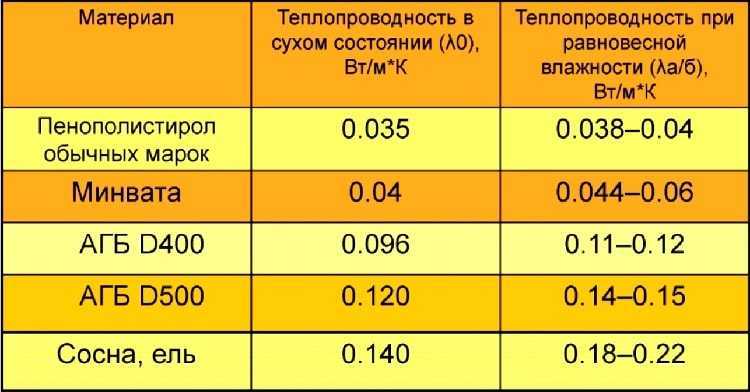 Кроме того, теплопроводность зависит от температуры. Теплопроводность увеличивается с повышением температуры!

Теплопроводность газов тем больше, чем меньше и легче молекулы и чем выше температура!

Зависимость теплопроводности от давления для низких давлений (разбавленные газы)

Если давление не влияет на теплопроводность газов, то зачем использовать вакуум для теплоизоляции?

Тот факт, что теплопроводность не зависит от давления, верен только до тех пор, пока длина свободного пробега много меньше размеров объема, в котором содержится газ. Если давление (плотность частиц) в сосуде все больше и больше снижается, частицы сталкиваются уже не друг с другом, а со стенками сосуда. Таким образом, при очень низких давлениях длина свободного пробега определяется размером контейнера, а не свободным пробегом между столкновениями двух частиц.

Это также применимо, если давление не уменьшено, а размер контейнера уменьшен. Это актуально, например, для изоляционных материалов, в которых газы заключены в мелкие поры.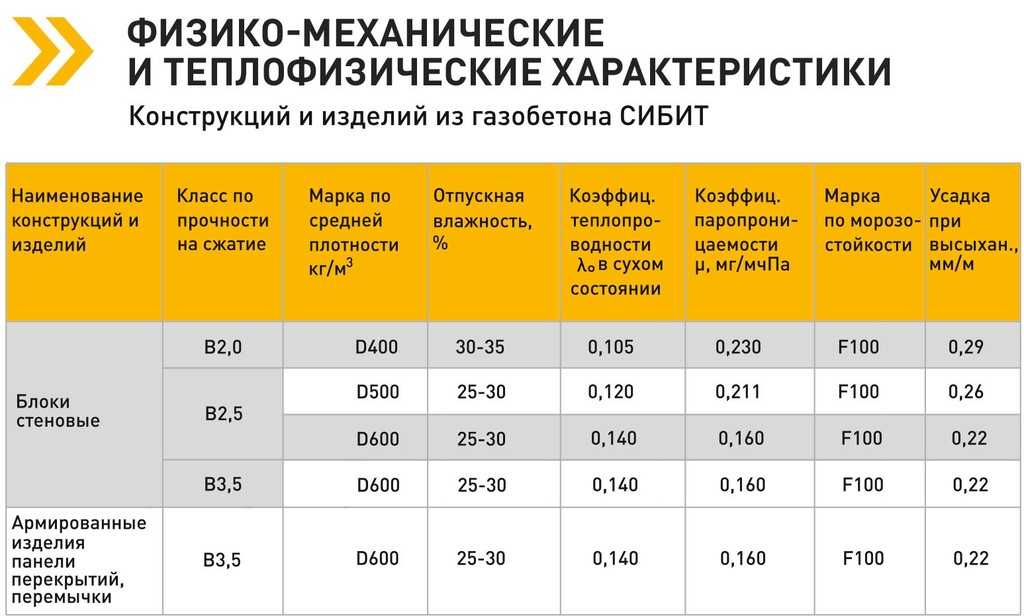 Такие ситуации также могут возникнуть с тонкими слоями фольги или небольшими зазорами, если между ними находится газ.

Рисунок: Влияние размеров контейнера на длину свободного пробега

Средняя длина свободного пробега в этих случаях приблизительно соответствует размеру δ объема (например, диаметру пор или зазору) и, следовательно, является постоянной величиной. В этом случае длина свободного пробега больше не зависит от плотности частиц: l≈δ=константа. При постоянной длине свободного пробега уравнение (\ref{ll}) указывает на уменьшение теплопроводности при уменьшении плотности частиц (или давления)!

\begin{align}
\label{a}
&\lambda = \frac{f}{6} k_B \cdot n \cdot v \cdot \delta \\[5px]
\end{align}

В разбавленных газах или при малых объемах газа теплопроводность зависит от давления!

В так называемых манометрах Пирани это соотношение используется для получения выводов о давлении в условиях высокого вакуума на основе теплопроводности.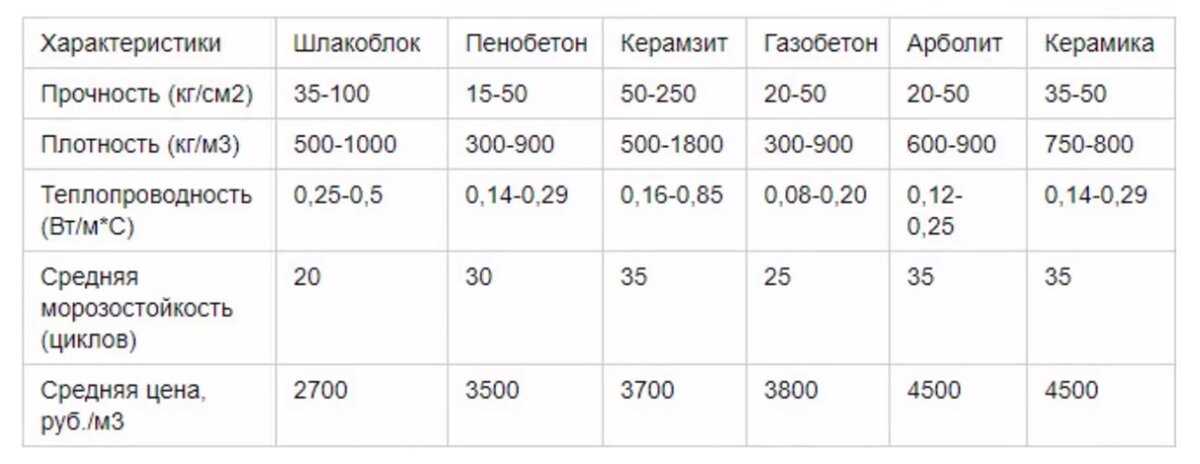

Номер Кнудсена

Как уже было указано, характерная длина δ пор или шаг фольги в изоляционных материалах часто намного меньше, чем длина свободного пробега l содержащихся в них газов. В этом случае газ уже не может быть описан как сплошная среда, так что уравнение (\ref{a}) уже не может применяться в таком виде (однако качественная формулировка этого уравнения не теряет своей силы).

Характеристическая длина относится к размеру/размеру системы!

В этом контексте так называемые Число Кнудсена указывает, можно ли по-прежнему рассматривать газ как континуум или следует применять кинетику газовой теории. Безразмерное число Кнудсена Kn описывает отношение длины свободного пробега l к характерной длине δ объема газа:

\begin{align}
&\boxed{Kn := \frac{l}{\delta}} \ \[5px]
\end{align}

Для значений намного меньших 1 по-прежнему применяется механика сплошной среды, а для значений намного больших 1 используется описание с помощью законов кинетической теории газов. 92 \cdot p \cdot \delta}} \\[5px]
\end{align}

В случае изоляционных материалов, где число Кнудсена часто намного меньше 1, теплопроводность заключенного газа может быть определяется по следующей формуле [см. М.Г. Каганер: « Теплоизоляция в криогенной технике », 1969]:

\begin{align}
\label{lam}
&\boxed{\lambda = \frac{\lambda_0}{1+2\beta \cdot Kn}} \\[5px]
\end{align}

В этой формуле λ ₀ обозначает теплопроводность при стандартных условиях (1 атм, 0°C), а β является весовым коэффициентом, который далее здесь обсуждаться не будет. Даже если использование уравнения (\ref{lam}) требует, чтобы число Кнудсена было намного меньше 1, оно все равно должно быть как можно больше, особенно для изоляционных материалов! Это приводит к низкой теплопроводности.

При низкой теплопроводности число Кнудсена должно быть максимально высоким!

Теплопроводность упорядоченных пористых структур, взаимодействующих с газовой и твердой фазами: исследование молекулярной динамики

Список журналов
Материалы (Базель)
PMC8123498

Материалы (Базель).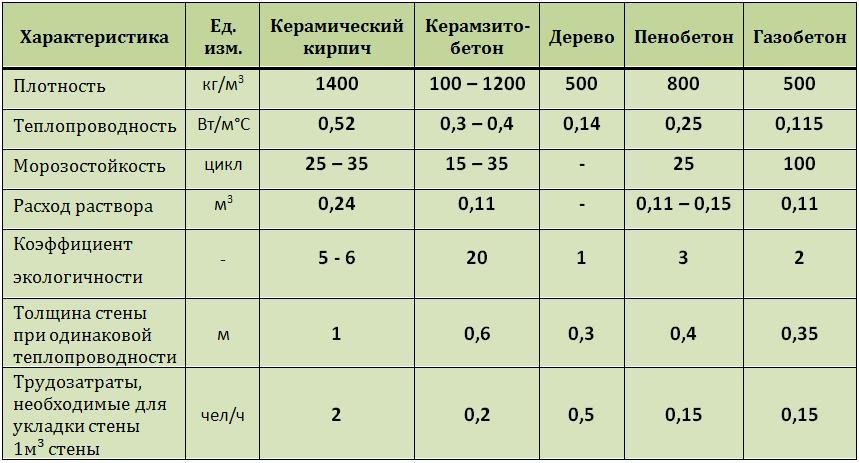 2021 май; 14(9): 2221.

Опубликовано в сети 26 апреля 2021 г. doi: 10.3390/ma14092221

Доминик Бейлис, академический редактор

Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности

Заявление о доступности данных

Теплопередача в пористой системе смеси твердого тела и газа является важным процессом для многих промышленных применений. Оптимизация конструкции теплоизоляционного материала очень важна во многих областях, таких как изоляция труб, тепловая защита космических кораблей и изоляция зданий. Понимание микромеханизма эффекта взаимодействия твердого тела с газом необходимо для разработки изоляционного материала. Прогнозирование теплопроводности для некоторых видов пористых материалов затруднено из-за взаимодействия твердого тела и газа. В этом исследовании метод Grand Canonical Monte Carlo (GCMC) и моделирование молекулярной динамики (MD) используются для исследования теплопроводности упорядоченных пористых структур пересекающихся квадратных стержней.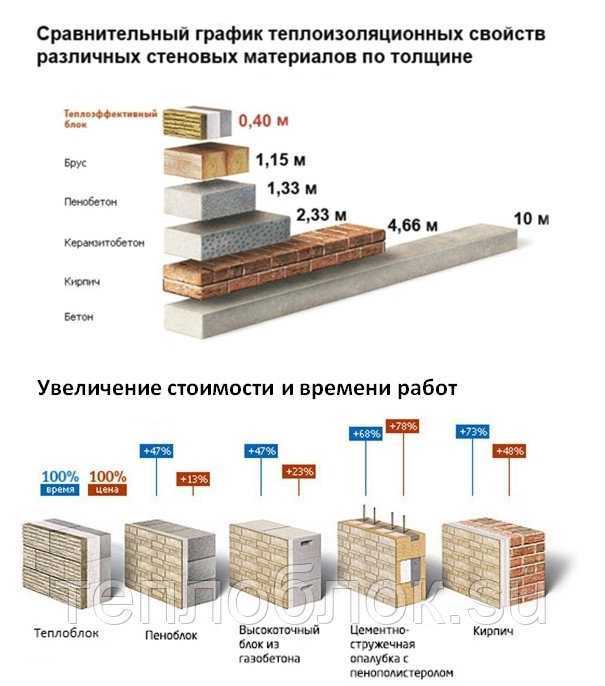 Выявлено влияние концентрации газа (давления) и взаимодействия твердого тела с газом на теплопроводность. Результаты моделирования показывают, что для различных структур каркаса влияние давления на теплопроводность представляет собой непоследовательный режим, который отличается от предыдущих исследований. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Это исследование обеспечивает возможность прямого расчета теплопроводности для пористых структур, связывающих газовую и твердую фазы, с использованием моделирования молекулярной динамики. Теплопередачу в пористых структурах, содержащих газ, можно понять на фундаментальном уровне.

Ключевые слова: теплопроводность, пористые структуры, молекулярно-динамическое моделирование, метод Грина-Кубо. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов.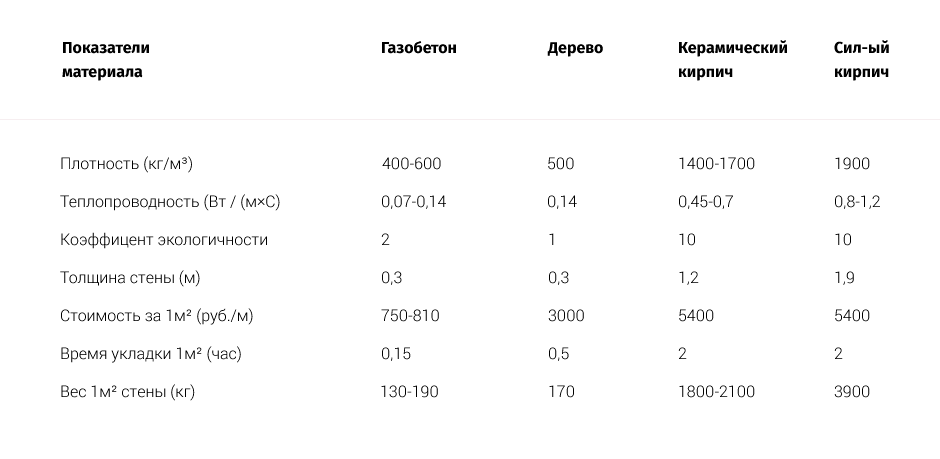 Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.

Большое количество теоретических моделей теплопроводности было разработано в предыдущих исследованиях [1, 2, 3, 4, 5, 6] с учетом влияния газа, твердого тела и излучения в непористом материале, в котором существуют некоторые отклонения по сравнению с с экспериментальным значением в некоторой степени. Из-за чрезвычайно сложных структур и эффекта взаимодействия твердого тела с газом в теоретической модели требуется множество эмпирических параметров, которые трудно определить. Численное моделирование является возможным выбором для непосредственного получения свойств нанопористых материалов. Решеточный метод Больцмана применялся для исследования фононного теплообмена в сферическом сегменте зерен аэрогеля нанокремнезема [7]. Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре. Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14]. Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.

Молекулярно-динамическое моделирование также является эффективным методом решения наноразмерных задач переноса тепла газами и твердыми телами. Кокил и др. [16] впервые применили моделирование неравновесной молекулярной динамики для предсказания теплопроводности аморфного нанопористого кремнезема. Результаты моделирования показали, что теплопроводность нанопористого кремнезема при комнатной температуре не зависит от размера пор и зависит только от пористости. Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности.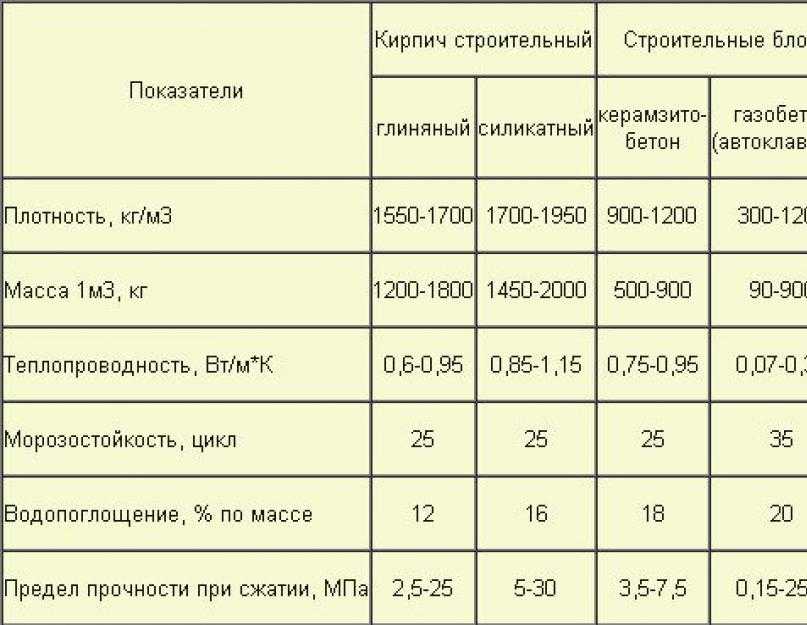 Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования. Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Снижение проводимости, связанное с увеличением концентрации газа, связано с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.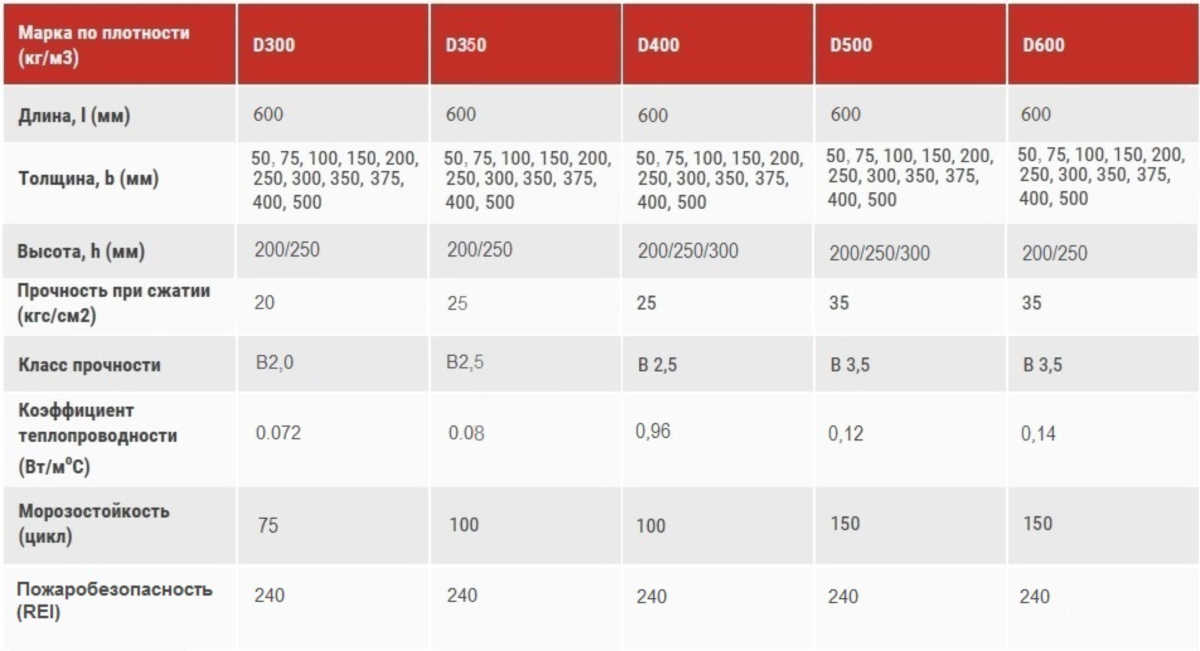

Несмотря на то, что было выполнено большое количество работ по теплопроводности нанопористых материалов, теоретическую модель особенно трудно использовать для непосредственного описания подробного взаимодействия газа и твердого тела, и большинство работ по моделированию сосредоточено только на одном компоненте. , твердое тело или газы. В этой работе мы проводим моделирование равновесной молекулярной динамики для изучения теплопроводности упорядоченных пористых структур, связывающих газовую и твердую фазы. Рассмотрено влияние давления и взаимодействия газа с твердым телом на теплопроводность.

Молекулярно-динамическое моделирование в данной работе выполнено с использованием пакета LAMMPS [21]. Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рис. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон.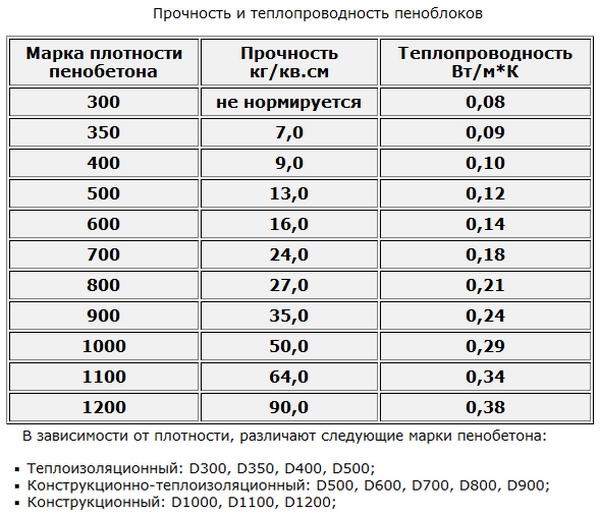 Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4 ε [( σ / r ) ¹² − ( σ / r ) ⁶ ] 14 Å. Подробные параметры, используемые в нашем моделировании, перечислены как в . Ансамбль NVT, который поддерживает постоянным число атомов, объем и температуру, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.

Открыть в отдельном окне

Настройка системы моделирования.

Таблица 1

Параметры, используемые при моделировании.

Material	ε (kcal/mol)	σ (Å)	l ( S )	L ( S )
Argon	0.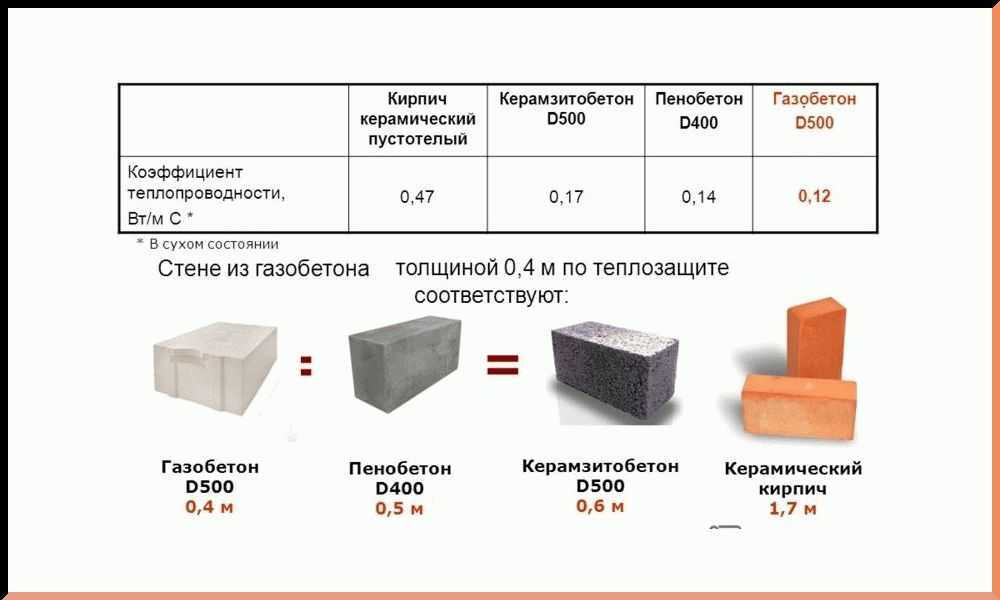 39	3.35	4, 5, 6, 7, 8	8, 12, 16, 20, 24
Helium	0.25	6.70
Аргон-Гелий	0,16	10,05

Открыть в отдельном окне

Теплопроводность нанопористой системы рассчитана по формуле Грин-Кубо

λ=VkbT2∫0∞〈j(0)j(t)〉dt

(1)

где k _b — постоянная Больцмана, V — объем ячейки моделирования, а угловые скобки обозначают среднее значение по времени. Микроскопический тепловой поток j получается из следующего уравнения

j(t)=1V(∑iviεi+12∑i∑j,j≠irij(vi·Fij))

(2)

где v _i — скорость атома i и F _ij — сила, действующая на атом i со стороны атома j . ε _i в первом члене уравнения (2) представляет собой энергию на атом, включая потенциальную и кинетическую энергию.

Для исследования теплопроводности нанопористой системы при различных давлениях все расчеты выполняются в два этапа. На первом этапе для определения газосодержания при различных давлениях используется симуляция Grand Canonical Monte Carlo. Алгоритм создает большой канонический ансамбль, в котором атомы газа могут быть перемещены, удалены или созданы в окне моделирования. На этом этапе на каждом шаге осуществляется большое количество попыток вставки и удаления атомов газа. Вставка или удаление атомов газа равновероятны в любом месте, если судить по обычным критериям Большого канонического алгоритма Монте-Карло.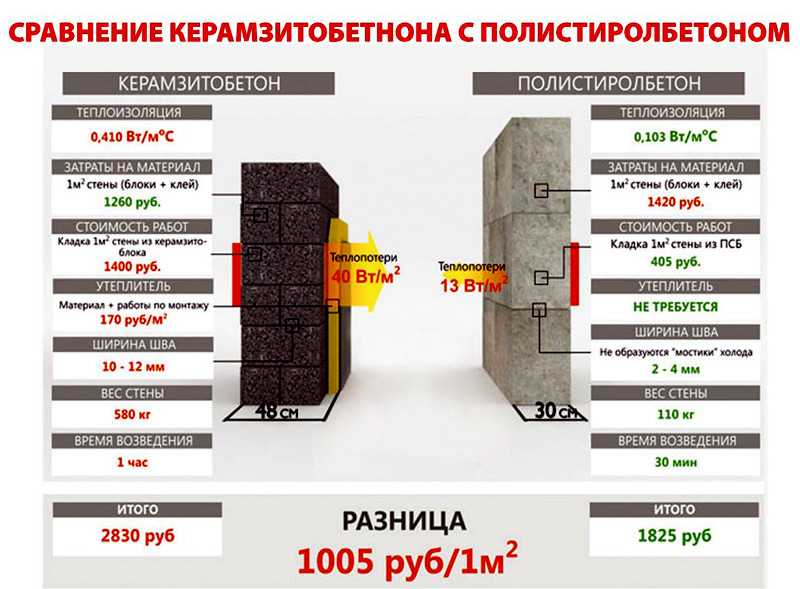 Газ гелия рассматривается как идеальный газ и химический потенциал μ можно определить, используя давление P , заданное формулой μ = k _b T ln( Pφ / k _{b φ} T ), где коэффициент fuga3 3 00 . Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 ⁷ временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.

показывает автокорреляционные функции теплового потока (HFACF), отвечающие уравнению (1) для нанопористой системы. Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0229 −1 K ⁻¹ после 20 пс.

Открыть в отдельном окне

ВТАКФ и погонная теплопроводность.

3.1. The Pressure Effect

и показывает распределение атомов газа в нанопористой системе ( L = 12 S , l = 4 S и L = 12 S 3 0 93 S , 9003 ). Мы используем постоянную решетки S в качестве радиуса отсечки для проведения кластерного анализа для системы газ-твердое тело. Атомы газа вблизи твердой фазы рассматриваются как адсорбированное состояние, а остальные рассматриваются как свободные атомы. Общее количество атомов газа в нанопористых системах увеличивается с давлением.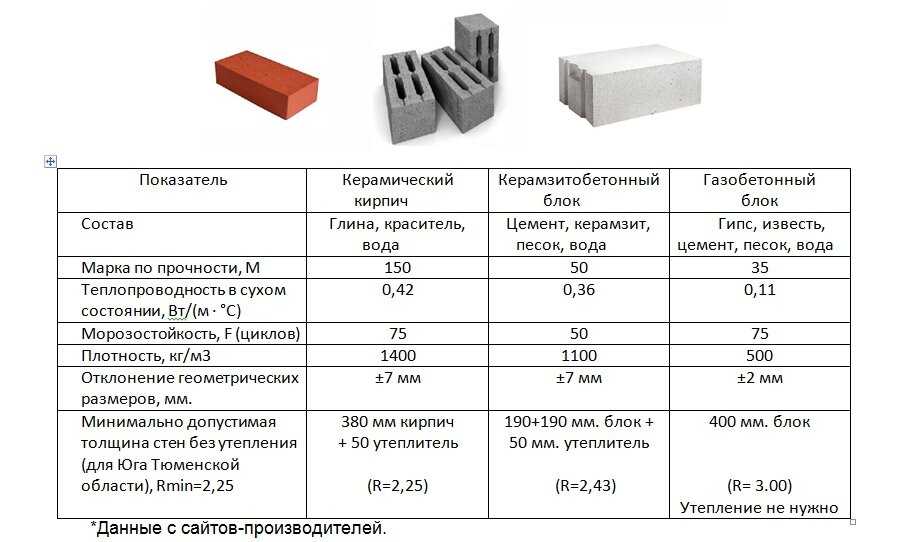 Однако для системы L = 12 S , l = 8 S , атомы свободного газа не зависят от давления из-за ограниченного пространства. Теплопроводность нанопористой системы ( л = 12 с , л = 4 с и л = 12 с , л = 8 с) как функция давления Показано в . Суммарная теплопроводность л = 8 С выше, чем у системы л = 4 S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0). Для нанопористой системы l = 4 S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для л = 8 С практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.

Открыть в отдельном окне

Распределение атомов газа в нанопористых системах.

Открыть в отдельном окне

Общее и количество свободных атомов газа в нанопористых системах.

Открыть в отдельном окне

Зависимость теплопроводности от давления.

3.2. Структурный эффект

На практике нанопористые материалы имеют различные структурные особенности в зависимости от метода и условий приготовления. Между тем структура также оказывает существенное влияние на общую теплопроводность нанопористой системы. Теплопроводность имитационной единицы, принимающей различные конструктивные параметры при одном и том же давлении, получается, как показано на и . Когда длина ( L ) блока моделирования теплопроводность системы сначала уменьшится и достигнет минимума около 10 S , а затем увеличится. Начальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность. По мере того, как длина ( L ) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины ( L ) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис.

Открыть в отдельном окне

Коэффициент теплопроводности для различных единиц длины ( л ).

Открыть в отдельном окне

Теплопроводность для разной ширины ( л ).

3.3. Взаимодействие газ-твердое тело

Чтобы соответствовать условиям применения, для нанопористых материалов может потребоваться модификация поверхности, в которой изменяется взаимодействие газ-твердое тело. До сих пор неясно, как зависит теплопроводность нанопористой системы от взаимодействия газ-твердое тело. В нашем моделировании энергетический параметр ε , используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε / ε _{газ-твердое тело} в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. и показать результаты распределения атомов газа и общей теплопроводности для различных ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличенным ε . Однако, как показано в , теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт м ^-1 К ^-1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, что вносит небольшой вклад в теплообмен в нанопористой системе. Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.

Открыть в отдельном окне

Распределение атомов газа для разных ε при давлении 2 атм.

Открыть в отдельном окне

Число атомов газа и теплопроводность для разных ε при давлении 2 атм.

В предыдущей работе [20] изучался теплообмен в пористых кристаллах, содержащих адсорбированные газы. Результаты показали, что в теплопроводности системы преобладает теплопроводность кристалла и снижается по мере увеличения концентрации газа в порах. Уменьшение проводимости при увеличении концентрации газа связано с фононным рассеянием кристалла, вызванным взаимодействием с атомами газа. В нашем моделировании аналогичные результаты не получены для пористой кристаллической системы. Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее. Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.

Чтобы дополнительно проиллюстрировать влияние взаимодействия газа и твердого тела на общую теплопроводность, случай постоянных атомов газа для различных взаимодействий газа и твердого тела исследуется, как показано на и . В системе L = 16 S , l = 4 S , мы можем найти, что атомы газа для ε / ε _{газ-твердое} = 0,3, что означает нижнюю поверхность энергии, может поддерживать свободное состояние. Однако для случая ε / ε _{газ-твердое} = 1, большинство атомов газа ограничены на поверхности и сохраняют поглощенное состояние, что не может способствовать теплообмену в пористых структурах, связывающих газовую и твердую фазы. Таким образом, общая теплопроводность резко уменьшается с 0,37 Вт·м·^-1··K·^-1· до 0,11 Вт·м·^-1··K·^-1· из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы.

Открыть в отдельном окне

Распределение атомов газа для различных ε при постоянном числе атомов газа.

Открыть в отдельном окне

Поглощенные атомы и теплопроводность для постоянных атомов газа.

В этой работе мы исследовали теплопроводность упорядоченных пористых структур с использованием Большого канонического метода Монте-Карло (GCMC) и моделирования молекулярной динамики (МД). Выявлено влияние концентрации газа, пористой структуры и взаимодействия газа с твердым телом на теплопроводность.

Результаты моделирования показывают, что для различных конструкций влияние давления на теплопроводность проявляется неравномерно. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.

Концептуализация, Х.Г. и Д.Н.; методика, Д.Н.; программное обеспечение, Д.Н.; валидация, HG и DN; формальный анализ, Д.Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.

Эта работа была поддержана Китайским фондом постдокторских наук (№ 2020M670725), Фондом ключевой лаборатории терможидкостной науки и техники (Сианьский университет Цзяотун), Министерством образования (KLTFSE2020KFJJ01), Фондами фундаментальных исследований для центральных университетов. (№3132019305).

Неприменимо.

Данные, представленные в этом исследовании, доступны по запросу у соответствующего автора.

Авторы заявляют об отсутствии конфликта интересов.

Примечание издателя: MDPI сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.

1. Райхенауэр Г., Хайнеманн У., Эберт Х.П. Связь между размером пор и зависимостью газовой теплопроводности от давления газа. Коллоидный прибой. А-Физикохим. англ. Асп. 2007; 300: 204–210. doi: 10.1016/j.colsurfa.2007.01.020. [Перекрестная ссылка] [Академия Google]

2. Чжао Дж.Дж., Дуань Ю.Ю., Ван X.Д., Ван Б.Х. Влияние взаимодействия твердого тела с газом, а также микроструктуры пор и частиц на эффективную газовую теплопроводность в аэрогелях. Дж. Нанопарт. Рез. 2012; 14:1–15. doi: 10.1007/s11051-012-1024-0. [CrossRef] [Google Scholar]

3. Bi C., Tang G.H., Hu Z.J., Yang H. L., Li J.N. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014;79:126–136. doi: 10.1016/j.ijheatmasstransfer.2014.07.098. [CrossRef] [Google Scholar]

4. Hümmer E., Lu X., Rettelbach T., Fricke J. Теплопередача в непрозрачных порошках аэрогеля. J. Некристалл. Твердые вещества. 1992; 145: 211–216. doi: 10.1016/S0022-3093(05)80458-2. [CrossRef] [Google Scholar]

5. Hemberger F., Weis S., Reichenauer G., Ebert H.P. Теплотранспортные свойства функционально градиентных углеродных аэрогелей. Междунар. Дж. Термофиз. 2009;30:1357–1371. doi: 10.1007/s10765-009-0616-0. [CrossRef] [Google Scholar]

6. Хаясе Г., Кугимия К., Огава М., Кодера Ю., Канамори К., Наканиши К. Теплопроводность полиметилсилсесквиоксановых аэрогелей и ксерогелей с различными размерами пор для практического применения в качестве тепловые суперизоляторы. Дж. Матер. хим. А. 2014;2:6525–6531. дои: 10.1039/C3TA15094A. [CrossRef] [Google Scholar]

7. Хан Ю.Ф., Ся С.Л., Тан Х.П., Лю Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б. 2013; 420:58–63. doi: 10.1016/j.physb.2013.03.015. [CrossRef] [Google Scholar]

8. Li Z.Y., Zhu C.Y., Zhao X.P. Теоретическое и численное исследование газовой теплопроводности в аэрогеле. Междунар. J. Тепломассообмен. 2017; 108:1982–1990. doi: 10.1016/j.ijheatmasstransfer.2017.01.051. [Перекрестная ссылка] [Академия Google]

9. Чжу С.Ю., Ли З.Ю., Тао В.К. Теоретические и DSMC исследования теплопроводности газа, заключенного в кубовидную нанопору. Дж. Теплопередача. 2017;139:052405. doi: 10.1115/1.4035854. [CrossRef] [Google Scholar]

10. Чжао С.П., Ли З.Ю., Лю Х., Тао В.К. Расчет теплопроводности методом трехмерного прямого моделирования Монте-Карло. Дж. Наноски. нанотехнологии. 2015;15:3299–3304. doi: 10.1166/jnn.2015.9679. [PubMed] [CrossRef] [Google Scholar]

11. Zhu C.Y., Li Z.Y., Pang H.Q., Pan N. Численное моделирование газовой теплопроводности аэрогелей. Междунар. J. Тепломассообмен. 2019;131:217–225. doi: 10.1016/j.ijheatmasstransfer.2018.11.052. [CrossRef] [Google Scholar]

12. Цюй З.Г., Фу Ю.Д., Лю Ю., Чжоу Л. Подход к прогнозированию эффективной теплопроводности аэрогелевых материалов с помощью модифицированного решеточного метода Больцмана. заявл. Терм. англ. 2018; 132:730–739. doi: 10.1016/j.applthermaleng.2018.01.013. [CrossRef] [Google Scholar]

13. Фанг В.З., Чжан Х., Чен Л., Тао В.К. Численные прогнозы теплопроводности кремнеземного аэрогеля и его композитов. заявл. Терм. англ. 2017; 115:1277–1286. doi: 10.1016/j.applthermaleng.2016.10.184. [Перекрестная ссылка] [Академия Google]

14. Тан Г.Х., Би С., Фу Б. Теплопроводность в тонкой пленке нанопористого кремния. Дж. Заявл. физ. 2013;114:184302. doi: 10.1063/1.4829913. [CrossRef] [Google Scholar]

15. Fu B., Tang G.H., Bi C. Теплопроводность в наноструктурированных материалах и анализ локального угла между тепловыми потоками. Дж. Заявл. физ. 2014;116:124310. doi: 10.1063/1.4896551. [CrossRef] [Google Scholar]

16. Coquil T., Fang J., Pilon L. Молекулярно-динамическое исследование теплопроводности аморфного нанопористого кремнезема. Междунар. J. Тепломассообмен. 2011;54:4540–4548. doi: 10.1016/j.ijheatmasstransfer.2011.06.024. [Перекрестная ссылка] [Академия Google]

17. Нг Т.Ю., Йео Дж.Дж., Лю З.С. Молекулярно-динамическое исследование теплопроводности аэрогеля нанопористого кремнезема, полученного разрывом при отрицательном давлении. J. Некристалл. Твердые вещества. 2012; 358:1350–1355. doi: 10.1016/j.jnoncrysol.2012.03.007. [CrossRef] [Google Scholar]

18. Liu M., Qiu L., Zheng X.H., Zhu J., Tang D.W. Исследование термического сопротивления в цепочке вторичных частиц кремнеземного аэрогеля методом молекулярной динамики. Дж. Заявл. физ. 2014;116:093503. дои: 10.1063/1.4894511. [CrossRef] [Google Scholar]

19. Рабани Р., Хейдаринеджад Г., Хартинг Дж., Ширани Э. Влияние жесткости стенки, массы и потенциальной силы взаимодействия на характеристики теплопередачи газа в наноразмерах.