Содержание
Угол трения. Конус трения — Студопедия
Поделись с друзьями:
Определение. Углом трения называется угол, образованный нормальной реакцией и наибольшей полной реакцией опорной поверхности .
Иначе, углом трения называется наибольший угол , который может образовать полная реакция опорной поверхности с нормалью этой поверхности
Полная реакция опорной поверхности всегда расположена в области угла трения (либо внутри угла трения, либо совпадает с одной из сторон этого угла).
Видно, что: .
Таким образом, тангенс угла трения равен коэффициенту трения скольжения.
Определение. Конус, ось которого является нормалью к поверхности, а образующая отклонена от нормали на угол, равный углу трения, называется конусом трения (рис. 57).
Полная реакция опорной поверхности всегда расположена в области конуса трения (либо внутри конуса, либо совпадает с одной из его образующих).
Если при движении тела по неподвижной поверхности в любом направлении коэффициент трения скольжения имеет одно и то же значение, то конус трения будет круговым конусом. Если в разных направлениях коэффициент трения скольжения имеет различные значения, то образующие конуса трения составляют с нормалью опорной поверхности различные углы, поэтому конус трения не будет круговым.
ЛИТЕРАТУРА
1. Тарг С.М. Краткий курс теоретической механики. – М.: «Высшая школа», 1986. –416с.
2. Яблонский А.А., Никифоров В.А. Курс теоретической механики, т.1 – М.: «Высшая школа», 1984, 343с.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ……………………
1.1. Сила и система сил………………………………………………………
1.2. Аксиомы статики,
2. СВЯЗИ И ИХ РЕАКЦИИ…………………………………………………..
3. СИСТЕМА СХОДЯЩИХСЯ СИЛ…………………………………………
3.1. Теорема о равновесии тела под действием сходящейся
системы сил…………………………………………………………….
..
3.2. Аналитические условия равновесия тела, загруженного
сходящейся системой сил………………………………………………
3.3. Теорема о трех непараллельных силах (правило трех сил)…………..
4. МОМЕНТ СИЛЫ……………………………………………………………
4.1. Момент силы относительно оси………………………………………..
4.2. Момент силы относительно полюса (центра, точки)…………………
4.3. Момент силы относительно полюса как векторное
произведение…………………………………………………………….
4.4. Связь между моментами силы относительно полюса и
относительно оси………………………………………………………..
4.6 Главный момент системы сил………………………………………….
4.6. Зависимость между главными моментами системы сил
относительно двух полюсов……………………………………………
4.7. Теорема Вариньона (частный случай)…………………………………
5. ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ СТАТИКИ. ЭКВИВАЛЕНТНЫЕ
СИСТЕМЫ СИЛ………………………………………………………..
5.1. Элементарные операции статики………………………………………
5.2. Эквивалентные преобразования. Эквивалентные системы сил.
Равнодействующая………………………………………………………
5.3. Обобщенная теорема Вариньона……………………………………….
6. УСЛОВИЯ РАВНОВЕСИЯ. УСЛОВИЯ РАВНОВЕСИЯ В ОБЩЕМ
И ЧАСТНЫХ СЛУЧАЯХ……………………………………………….
6.1. Основная лемма статики…………………………………………………
6.2. Основная теорема статики………………………………………………
6.3. Аналитические условия равновесия произвольной системы сил
6.4. Частные случаи аналитических условий равновесия………………….
7. ОБЩИЙ ПРИЗНАК ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СИЛ……
8. ТЕОРИЯ ПАР СИЛ…………………………………………………………..
8.1. Момент пары сил…………………………………………………………
8.2. Признак эквивалентности двух пар сил…………………………………
8.3. Следствия из признака эквивалентности пар……………………………
8.4. Теорема о «сложении» пар………………………………………………..
9. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ…………….
9.1. Лемма о параллельном переносе силы…………………………………..
9.2. Теорема Пуансо…………………………………………………………….
9.3. Частные случаи приведения системы сил к заданному центру…………
9.
4. Инварианты системы сил…………………………………………………..
10. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ. ЦЕНТР ТЯЖЕСТИ………………………
10.1. Центр параллельных сил…………………………………………………..
10.2. Центр тяжести твердого тела………………………………………………
10.3. Статические моменты………………………………………………………
10.4. Центры тяжести симметричных тел……………………………………….
10.5. Основные способы определения центра тяжести…………………………
11. ТРЕНИЕ СКОЛЬЖЕНИЯ………………………………………………………
11.1. Сила трения и коэффициент трения……………………………………….
11.2. Угол трения. Конус трения………………………………………………….
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
22.Угол и конус трения
Реакция
реальной (шероховатой) связи будет
слагаться из двух составляющих: из
нормальной реакции и
перпендикулярной к ней силы трения .
Следовательно, полная реакция будет
отклонена от нормали к поверхности на
некоторый угол.
При изменении силы
трения от нуля до Fпр сила R будет
меняться от N до Rпр,
а ее угол с нормалью будет расти от нуля
до некоторого предельного
значения (рис.
26).
Рис.26
Наибольший
угол ,
который полная реакция шероховатой
связи образует с нормалью к поверхности,
называется углом
трения. Из чертежа
видно, что
.
Так
как ,
отсюда находим следующую связь между
углом трения и коэффициентом трения:
При
равновесии полная реакция R,
в зависимости от сдвигающих сил, может
проходить где угодно внутри угла трения.
Когда равновесие становится предельным,
реакция будет отклонена от нормали на
угол .
Конусом
трения называют
конус, описанный предельной силой
реакции шероховатой связи вокруг
направления нормальной реакции.
Если
к телу, лежащему на шероховатой
поверхности, приложить силу Р,
образующую угол с
нормалью (рис. 27), то тело сдвинется
только тогда, когда сдвигающее
усилие Psin будет
больше (мы
считаем N=Pcos,
пренебрегая весом тела). Но неравенство ,
в котором ,
выполняется только при ,
т.е. при .
Следовательно, никакой силой,
образующей с нормалью угол ,
меньший угла трения ,
тело вдоль данной поверхности сдвинуть
нельзя. Этим объясняются известные
явления заклинивания или самоторможения
тел.
Рис.27
Для равновесия
твёрдого тела на шероховатой поверхности
необходимо и достаточно, чтобы линия
действия равнодействующей активных
сил, действующих на твёрдое тело,
проходила внутри конуса трения или по
его образующей через его вершину.
Тело нельзя вывести
из равновесия любой по модулю активной
силой, если её линия действия проходит
внутри конуса трения.
происхождение
трения качения можно наглядно представить
себе так. Когда шар или цилиндр катится
по поверхности другого тела, он немного
вдавливается в поверхность этого тела,
а сам немного сжимается. Таким образом,
катящееся тело всё время как бы вкатывается
на горку.
Рис.33
Вместе с тем
происходит отрыв участков одной
поверхности от другой, а силы сцепления,
действующие между этими поверхностями,
препятствуют этому. Оба эти явления и
вызывают силы трения качения. Чем твёрже
поверхности, тем меньше вдавливание и
тем меньше трение качения.
Трением
качения называется
сопротивление, возникающее при качении
одного тела по поверхности другого.
Рис.34
Рассмотрим
круглый цилиндрический каток радиуса R и
веса ,
лежащий на горизонтальной шероховатой
плоскости. Приложим к оси катка
силу (рис.
34, а), меньшую Fпр.
Тогда в точке А возникает
сила трения ,
численно равная Q,
которая будет препятствовать скольжению
цилиндра по плоскости. Если считать
нормальную реакцию тоже
приложенной в точке А,
то она уравновесит силу ,
а силы и образуют
пару, вызывающую качение цилиндра. При
такой схеме качение должно начаться,
как видим, под действием любой, сколь
угодно малой
силы .
Истинная
же картина, как показывает опыт,
выглядит иначе. Объясняется это тем,
что фактически, вследствие деформаций
тел, касание их происходит вдоль некоторой
площадки АВ (рис.
34, б). При действии силы интенсивность
давлений у края А убывает,
а у края В возрастает.
В результате реакция оказывается
смещенной в сторону действия силы .
С увеличением это
смещение растет до некоторой предельной
величины k.
Таким образом, в предельном положении
на каток будут действовать пара (, )
с моментом и
уравновешивающая ее пара ()
с моментом Nk.
Из равенства моментов находим или
Пока ,
каток находится в покое; при начинается
качение.
Входящая
в формулу линейная
величина k называется коэффициентом
трения качения. Измеряют
величину k обычно
в сантиметрах. Значение
коэффициента k зависит
от материала тел и определяется
опытным путем.
Коэффициент трения
качения при качении в первом приближении
можно считать не зависящим от угловой
скорости качения катка и его скорости
скольжения по плоскости.
Для
вагонного колеса по рельсу k=0,5
мм.
Рассмотрим
движение ведомого колеса.
Качение
колеса начнется, когда выполнится
условие QR>M или Q>Mmax/R=kN/R
Скольжение
колеса начнется, когда выполнится
условие Q>Fmax=fN.
Обычно
отношение и
качение начинается раньше скольжения.
Если , то колесо
будет скользить по поверхности, без
качения.
Отношение для
большинства материалов значительно
меньше статического коэффициента
трения .
Этим объясняется то,
что в технике, когда это возможно,
стремятся заменить скольжение качением
(колеса, катки, шариковые подшипники и
т. п.).
24.Понятие
о фермах и их классификация
При
больших пролетах и значительных нагрузках
балки сплошного сечения становятся
экономически невыгодными. В таких
случаях их заменяют сквозной конструкцией
– стержневой системой (фермой), элементы,
которых при узловых нагрузках работают
на центральное сжатие и растяжение.
Фермой
называется геометрически неизменимая
система, составленная из стержней,
шарнирно соединенных между собой.
При
расчетах ферм принимают, что узлы
являются идеально гладкими, лишенными
трения, а оси всех стержней проходят
через геометрические центры шарниров.
Такой
расчетной схемой будем пользоваться
на протяжении дальнейшего расчета.
На
практике обычно ферме придают такое
устройство, чтобы нагрузка передавалась
на нее исключительно в узлах.
При таком
устройстве любая нагрузка будет вызывать
в любом стержне только продольные
усилия.
Кроме плоских ферм,
у которых оси всех стержней расположены
в одной плоскости, применяются пространственные фермы,
оси элементов которых не лежат в одной
плоскости. Расчет пространственных
ферм часто удается свести к расчету
нескольких плоских ферм.
Расстояние
между осями опор фермы называется пролетом.
Стержни, расположенные по внешнему
контуру фермы, называется поясными, и
образуют пояса.
Стержни,
соединяющие пояса, образуют решетку
фермы и называются: вертикальные –
стойками, наклонные – раскосами.
Расстояние между соседними узлами
любого пояса фермы называется
панелью.
Стержни,
ограничивающие контур фермы сверху,
образуют ее верхний пояс, а снизу –
нижний. Внутренние стержни образуют
решетку, вертикальные стержни которой
называется стойками, наклонные –
раскосами. Расстояние по горизонтами
м/у соседними узлами любого пояса
называется длиной панели.
Классификация:
1)
по очертаний поясов;
2) по типу решетки:
раскосные, полураскосные, многораскосные
с треугольными решетками, с составной
(шпренгельной) решеткой;
3) по назначению
– мостовые, стропильные, башенные и
т.
д;
4) по условию опирания – балочные,
арочные, консольные, балочно-консольный.
Угол внутреннего трения | Угол сопротивления сдвигу
Одним из важных параметров, считающихся типичным свойством сыпучих грунтов, является угол внутреннего трения ϕ. Способность массива горной породы или грунта выдерживать напряжение сдвига можно измерить по углу внутреннего трения (также называемому углом сопротивления сдвигу). Когда разрушение происходит в ответ на касательное напряжение (τ), угол (ϕ), измеренный между нормальной силой (σ) и равнодействующей силой (R), называется углом внутреннего трения.
Коэффициент трения скольжения равен его тангенсу (τ/σ). Угол внутреннего трения любого грунта можно увидеть визуально на графике круга Мора после испытания на сопротивление сдвигу.
Рисунок 1: Круг Мора для напряжения грунта
Экспериментальный анализ, такой как трехосное испытание, используется для определения значения угла внутреннего трения. Прежде чем приступить к аналитическим и проектным процессам в отношении фундаментов, подпорных стен, устойчивости откосов и подпорных конструкций, необходимо определить параметры прочности на сдвиг.
Физической характеристикой земных материалов или наклоном линейного представления их прочности на сдвиг является угол внутреннего трения.
Внутреннее сопротивление, которое грунтовая масса может обеспечить на единицу площади, чтобы выдержать разрушение по любой внутренней плоскости, известно как сопротивление сдвигу. Отказ происходит, когда это сопротивление превышено. Максимальное или предельное значение напряжения сдвига, создаваемого в матрице грунта до текучести, называется прочностью на сдвиг грунта. Силы сцепления и трения между соседними частицами в матрице грунта придают конструкции прочность на сдвиг.
В результате существует некоторая зависимость поверхности от прочности грунта на сдвиг. Любое действие, которое предотвращает или способствует сцеплению или слипанию частиц почвы, неизбежно повлияет на прочность почвы на сдвиг.
Прочность на сдвиг обычно включает:
(a) внутреннее трение или сопротивление за счет сцепления частиц, представленное углом ϕ;
(b) сцепление или сопротивление из-за сил, стремящихся удерживать частицы вместе в твердой массе.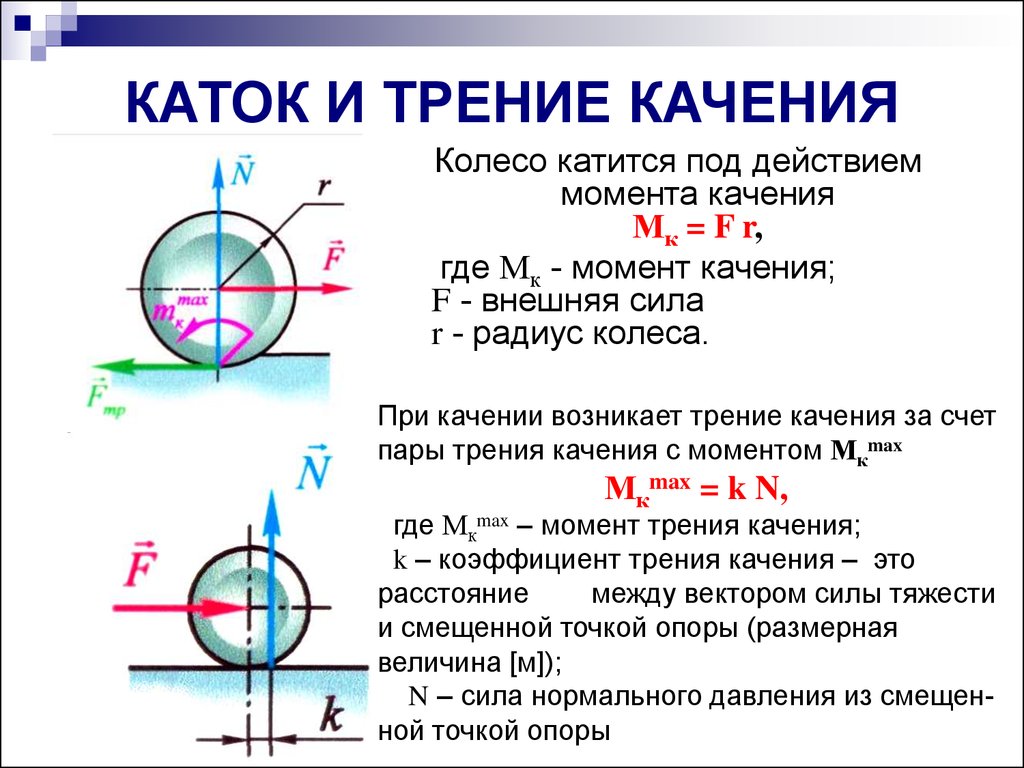
Связность почвы обычно обозначается буквой «с».
Кулон был первым, кто предложил закон разрушения грунтов при сдвиге, который представлен уравнением;
τ = c + σtanϕ ——— (1)
, где нормальная сила равна σ, а прочность на сдвиг равна τ.
Инженеры и геологи обычно называют рыхлые и несцементированные земные материалы почвой, а геологи могут называть такие материалы отложениями. Различные размеры (мм до m) от очень мелких до очень крупных минералов или фрагментов горных пород составляют почву (глина, ил, песок, гравий, булыжник и размер валуна).
Масса зерен, химически и механически отличающихся друг от друга, может быть относительно легко извлечена, а удаленный материал может быть сложен в коническую форму с наклоном, известным как угол естественного откоса (рис. 2). Угол естественного откоса представляет собой угол внутреннего трения, но обычно он контролируется формой зерна, в результате чего наклоны обычно составляют от 28 ° до 34 ° для куч рыхлых сухих зерен в естественной почве.
Рисунок 2 : Груда гравия образует угол естественного откоса
Угол внутреннего трения определяется как угол между нормальной силой реакции и комбинированной силой трения и нормальной силой реакции, когда объект начинает двигаться, тогда как угол покоя определяется как минимальный угол наклонной плоскости, при котором объект скользит по плоскости. Теоретически угол внутреннего трения и угол естественного откоса, по-видимому, означают одно и то же. Однако угол внутреннего трения, определенный при испытаниях, используется для геотехнических расчетов.
Распределение размера зерен, угловатость и сцепление частиц являются основными переменными, которые помимо плотности влияют на угол трения грунта. Как вы можете догадаться, мелкозернистый и хорошо окатанный песок имеет меньший угол трения, чем угловатый и крупнозернистый песок.
Рисунок 3: Зависимость между углом естественного откоса и прочностью грунта
φ = 45° Выберите гранулированный грунт.
Уклон, φ, может быть даже больше, если грунт хорошо уплотнен.
φ = 30° Хорошая почва. Почва может быть неуплотненной или, возможно, влажной.
φ = 15° Плохая почва. Плохая почва может содержать высокий процент мелких частиц и может быть влажной.
φ = 0° Грязь. Почва жидкая и не имеет угла наклона, φ
Угол внутреннего трения для различных типов грунта можно оценить с помощью инженерно-геологических испытаний на месте. Некоторые из них показаны в таблице 1;
| Описание | Относительная плотность | SPT – N (ударов/300 мм) | ||
| Очень рыхлая | < 15 % | N ≤ 4 | φ < 28° 4 – 10 | φ = 28 – 30° |
| Среднеплотный | 35–65% | N = 10–30 | φ = 30–40° | |
| Плотный | φ =40 – 45° | |||
| Очень плотный | > 85% | N > 50 | φ = 45 – 50° |
Таблица 1: Угол внутреннего трения по данным SPT
Угол внутреннего трения для разных классификаций грунта представлен в таблице 2;
| Группа грунтов Обозначение | Сцепление (насыщенное) кПа | Угол внутреннего трения (φ) 905 G | 0 | > 38° |
| GP | 0 | > 37° |
| GM | – | > 34° |
| GC | ||
| SW | 0 | 38° |
| SP | 0 | 37° |
| SM | 20 | 34° |
| SM-SC 1 30 19931 40130 33° | ||
| SC | 11 | 31° |
| ML | 9 | 32° |
| ML-CL | 22 | 32° | 28° |
| ПР | – | – |
| MH | 20 | 25° |
| CH | 11 | 19° |
Таблица 2: Угол внутреннего трения для разных классификаций грунта
Угол трения
Угол трения
Угол трения грунта — это параметр прочности грунта на сдвиг.
Его определение получено из критерия разрушения Мора-Кулона и используется для описания сопротивления грунта сдвигу трения вместе с нормальным эффективным напряжением. Угол трения грунта равен параметр прочности грунтов на сдвиг.Его определение получено из критерия разрушения Мора-Кулона и используется для описания сопротивления грунтов трению сдвигу вместе с нормальным эффективным напряжением.
В плоскости напряжения эффективного нормального напряжения сдвига угол трения грунта представляет собой угол наклона по отношению к горизонтальной оси линии сопротивления сдвигу Мора-Кулона.
Типовые значения угла трения грунта
Некоторые типичные значения угла трения грунта приведены ниже для различных типов грунта USCS в нормально уплотненном состоянии, если не указано иное. Эти значения следует использовать только в качестве ориентира при решении геотехнических задач; однако часто необходимо учитывать конкретное состояние каждой инженерной задачи для соответствующего выбора геотехнических параметров.
| Описание | USCS | Угол трения о грунт [°] | Артикул | ||
| мин | макс. | Конкретное значение | |||
| Хорошо отсортированный гравий, песчано-гравийный, с небольшим содержанием мелких частиц или без них | ГВт | 33 | 40 | [1], [2], | |
| Гравий плохого качества, песчано-гравийный, с небольшим содержанием мелких частиц или без них | ГП | 32 | 44 | [1], | |
| Песчаный гравий — сыпучий | (ГВ, ГП) | 35 | [3 цитируется в 6] | ||
| Песчаный гравий — плотный | (ГВ, ГП) | 50 | [3 цитируется в 6] | ||
| Илистый гравий, илистый песчаный гравий | ГМ | 30 | 40 | [1], | |
| Глинистый гравий, глинисто-песчаный гравий | ГК | 28 | 35 | [1], | |
| Хорошо отсортированные пески, гравийные пески, с небольшим содержанием мелких частиц или без них | SW | 33 | 43 | [1], | |
| Хорошо отсортированный чистый песок, гравийные пески — уплотненный | SW | — | — | 38 | [3 цитируется в 6] |
| Песок хорошо отсортированный, угловатые зерна — сыпучий | (ПО) | 33 | [3 цитируется в 6] | ||
| Песок хорошего качества, угловатые зерна — Плотный | (ПО) | 45 | [3 цитируется в 6] | ||
| Пески плохого качества, гравийные пески с небольшим содержанием мелких частиц или без них | СП | 30 | 39 | [1], [2], | |
| Плохо засаханный чистый песок — уплотненный | СП | — | — | 37 | [3 цитируется в 6] |
| Однородный песок, круглозернистый — Сыпучий | (СП) | 27 | [3 цитируется в 6] | ||
| Однородный песок, круглозернистый — Плотный | (СП) | 34 | [3 цитируется в 6] | ||
| Песок | ПО, СП | 37 | 38 | [7], | |
| Песок сыпучий | (ЮЗ, СП) | 29 | 30 | [5 цитируется в 6] | |
| Средний песок | (ЮЗ, СП) | 30 | 36 | [5 цитируется в 6] | |
| Плотный песок | (ЮЗ, СП) | 36 | 41 | [5 цитируется в 6] | |
| Илистые пески | СМ | 32 | 35 | [1], | |
| Алевритистые глины, песчано-алевритовые смеси — уплотненные | СМ | — | — | 34 | [3 цитируется в 6] |
| Илистый песок — Сыпучий | СМ | 27 | 33 | [3 цитируется в 6] | |
| Илистый песок — Плотный | СМ | 30 | 34 | [3 цитируется в 6] | |
| Глинистые пески | СК | 30 | 40 | [1], | |
| Пески глинистые, смесь песчано-глинистая — уплотненная | СК | 31 | [3 цитируется в 6] | ||
| Суглинистый песок, супесь Суглинок | СМ, СК | 31 | 34 | [7], | |
| Илы неорганические, алевритовые или глинистые мелкозернистые пески со слабой пластичностью | мл | 27 | 41 | [1], | |
| Ил неорганический — сыпучий | мл | 27 | 30 | [3 цитируется в 6] | |
| Ил неорганический — плотный | мл | 30 | 35 | [3 цитируется в 6] | |
| Неорганические глины, алевритистые глины, песчаные глины низкой пластичности | класс | 27 | 35 | [1], | |
| Глины малопластичные — уплотненные | класс | 28 | [3 цитируется в 6] | ||
| Органические илы и органоалевритистые глины низкой пластичности | ОЛ | 22 | 32 | [1], | |
| Неорганические илы высокой пластичности | МХ | 23 | 33 | [1], | |
| Илы глинистые — уплотненные | МХ | 25 | [3 цитируется в 6] | ||
| Илы и глинистые илы — уплотненные | мл | 32 | [3 цитируется в 6] | ||
| Глины неорганические высокопластичные | Ч | 17 | 31 | [1], | |
| Глины высокопластичные уплотненные | Ч | 19 | [3 цитируется в 6] | ||
| Глины органические высокопластичные | ОХ | 17 | 35 | [1], | |
| Суглинок | МЛ, ПР, МЗ, ОХ | 28 | 32 | [7], | |
| Илистый суглинок | МЛ, ПР, МЗ, ОХ | 25 | 32 | [7], | |
| Суглинок, Илистый суглинок | ML, OL, CL, MH, OH, CH | 18 | 32 | [7], | |
| Илистая глина | ПР, КЛ, ОХ, CH | 18 | 32 | [7], | |
| Глина | CL, CH, OH, OL | 18 | 28 | [7], | |
| Торф и другие высокоорганические почвы | Пт | 0 | 10 | [2], | |
Корреляция между значением SPT-N, углом трения и относительной плотностью
| SPT N3 [Удары/0,3 м — 1 фут] | Сои упаковка | Относительная плотность [%] | Угол трения |
|---|---|---|---|
< 4 | Очень свободный | < 20 | < 30 |
4–10 | Свободно | 20 — 40 | 30 — 35 |
10 — 30 | Компактный | 40 — 60 | 35 — 40 |
30 — 50 | Плотный | 60 — 80 | 40 — 45 |
> 50 | Очень плотный | > 80 | > 45 |
Ссылки
- Швейцарский стандарт SN 670 010b, Характеристические коэффициенты почв, Ассоциация швейцарских инженеров-дорожников Швейцарский стандарт SN 670 010b, Характеристические коэффициенты почв, Ассоциация швейцарских инженеров-дорожников1 9104
- ДЖОН В.
