ГлавнаяРазноеКоэффициент упругости таблица

Элементы теории упругости. Коэффициент упругости таблица


Коэффициент жесткости пружины, формула и примеры

Определение и формула коэффициента жесткости пружины

Сила упругости (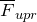{\overline{F}}_{upr}), которая возникает в результате деформации тела, в частности пружины, направленная в сторону противоположную перемещению частиц, деформируемого тела, пропорциональна удлинению пружины:

    \[{\overline{F}}_{upr}=-kx\left(1\right)\]

Он зависит от формы тела, его размеров, материала из которого изготовлено тело (пружина).

Иногда коэффициент жесткости обозначают буквами D и с.

Величина коэффициента жёсткости пружины указывает на устойчивость ее к действию нагрузок и насколько велико ее сопротивление при воздействии.

Коэффициент жесткости соединений пружин

Если некоторое число пружин соединить последовательно, то суммарную жесткость такой системы можно вычислить как:

    \[\frac{1}{k}=\sum^N_{i=1}{\frac{1}{k_i}}\left(3\right)\]

В том случае, если мы имеем дело с n пружинами, которые соединены параллельно, то результирующую жесткость получают как:

    \[k=\sum^N_{i=1}{k_i}\left(4\right)\]

Коэффициент жесткости цилиндрической пружины

Рассмотрим пружину в виде спирали, которая сделана из проволоки с сечением круг. Если рассматривать деформацию пружины как совокупность элементарных сдвигов в ее объеме под воздействие сил упругости, то коэффициент жесткости можно вычислить при помощи формулы:

    \[k=\frac{r^4}{4R^3}\frac{G}{n}\left(5\right),\]

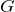где R — радиус пружины, n — количество витков в пружине, r — радиус проволоки, G — модуль сдвига (постоянная, которая зависит от материала).

Единицы измерения

Основной единицей измерения коэффициента жесткости в системе СИ является:

    \[\left[k\right]=\frac{H}{m}=\frac{kg}{c^2}\]

В СГС:

\left[k\right] = дин/см

Примеры решения задач

ru.solverbook.com

Коэффициент упругости - Справочник химика 21

Рис. 61. Коэффициент упругого расширения кокса, полученного в кубе из крекинг-остатка сернистой девонской нефти и прокаленного при 1300 °С в течение 5 ч Рис. 61. Коэффициент упругого расширения кокса, полученного в кубе из крекинг-остатка сернистой <a href="/info/1462682">девонской нефти</a> и прокаленного при 1300 °С в течение 5 ч
    Фридман Я.Б. Специальные стали, имеющие аномалии теплового рас ширения и температурного коэффициента упругости (к теории инвара и и элинвара). - Качественная сталь, 1937, № I, с.47-54. [c.80]

    Вследствие малой деформации твердой фазы считают обычно, что изменение пористости зависит от изменения давления линейно. Закон сжимаемости породы записывают следующим образом, вводя коэффициент упругости пласта [c.52]

    Изучение прессовых характеристик нефтяного кокса (коэффициента упругого расширения, коэффициента релаксации и коэффициента прочности частиц) было начато в 1939 г. в связи с выяснением причин брака при изготовлении прессованных анодов на одном из электродных заводов. В настоящее время на алюминиевых заводах используют почти исключительно самообжигающиеся непрессованные аноды. Но электродные заводы выпускают прессованную продукцию в сильно возросшем количестве и ассортименте для использования в производстве графитированных изделий. Поэтому значение работ по прессовым характеристикам нефтяного кокса возросло. [c.173]

    Здесь искомая функция р(х,у,1) соответствует давлению к = ко(х,у)1т, ) = Р = т+ (3 - коэффициент упругости пласта /-плотность источников и стоков, моделирующих работу добывающих и нагнетательных скважин. Со способами моделирования скважин можно познакомиться по книге [45]. [c.391]

    Здесь б — толщина кожуха бц — толщина эластичной прослойки — модуль упругости материала прослойки в нагретом состоянии V — коэффициент упругости материала прослойки в нагретом состоянии, равный отношению упругих деформаций прослойки при сжатии к ее полным деформациям г — радиус кожуха. [c.247]

    Простейшей колебательной системой служит гармонический осциллятор - масса т, закрепленная на пружине с коэффициентом упругости к (рис. 2.1). Дифференциальное уравнение собственных колебаний в [c.29]

    Т л б л и ц i 1. Коэффициенты упругости монокристаллов некоторых гексагональных металлов, ГПа [I] [c.258]

    Коэффициент упругого расширения, % Коэффициент релаксации, %. ... Временное сопротивление сжатию,  [c.135]

    Коэффициент упругого расширения Ку. р. находили из соотношения [c.175]

    Рис, 60. Коэффициент упругого расширения кокса, прокаленного при 1300 °С в течение 5 ч (фракция 1—1,5 мм)-. [c.178]

    На рис. 65—67 представлены значения коэффициентов упругого расширения после снятия нагрузки и коэффициентов ре лаксации. При этом были выявлены следующие закономерности. Коэффициент упругого расширения после снятия нагрузки по мере повышения температуры прокалки вначале сни- [c.183]

    Увеличение степени волокнистости кокса, как и всякого другого твердого тела, обладающего упругими свойствами, приводит к увеличению эффекта упругого последействия. Объем такого тела в большей степени восстанавливается после снятия нагрузки. Симметрично построенные тела обладают большей прочностью и меньшим коэффициентом упругого расширения. [c.186]

    Е — коэффициент упругости материала  [c.255]

    В табл. 1 и 2 (см. с. 258) приведены коэффициенты упругости монокристаллов соответственно гексагональных и кубических структур [1,2 . Эти данные приведены для того, чтобы дать представление о диапазоне, в котором может проявиться упругая анизотропия в поли-кристаллических материалах с преимущественной ориентацией зерен. [c.255]

    Для нефтяного кокса как хрупкого материала необходимо знать такие показатели его механических свойств, как прочность и коэффициенты упругого расширения, релаксации, прочности частиц и прессовой добротности. [c.40]

    Коэффициенты упругого расширения и релаксации, отражающие прессовые и пластические свойства кокса, детально исследованы А. Ф. Красюковым [3, 681. [c.44]

    По нашему убеждению, перечисленный перечень характеристик кокса достаточно полно отражает свойства нефтяных коксов анодного качества. Понятно, что перечень известных методик не ограничивается теми методами, которые предлагаются для включения в новый ГОСТ. Такие показатели как распределение пор по диаметрам, прессовые характеристики (коэффициент релаксации, коэффициент упругого расширения, коэффициент прессовой добротности), удельная адсорбция и др. могут применяться в исследовательских целях и для настройки технологии. [c.37]

    Коэффициент упругого разрушения /Су,р характеризует упругие свойства кокса после снятия нагрузки. В связи с тем что упругие свойства коксов определяют в последующем структуру и качество электродов, коэффициент упругого расширения для различных коксов имеет непосредственно практическое значение. [c.180]

    Коэффициент упругого расширения [c.193]

    Коэффициент упругого расширения Кур характеризует упругие свойства кокса после снятия нагрузки. В связи с тем, что упругие свойства коксов определяют в последующем структуру и качество электродов, величина коэффициента упругого расширении для различных коксов имеет непосредственное практическое значение, хотя эта константа и не входит в показатели качества коксов по ГОСТ. [c.193]

    Щ)и рассмотрении упругих колебаний и волн в различных системах выделяют предельный случай, когда можно пренебречь волновьл характером явлений вследствие их большой скорости распространения и малых размеров системы. Тогда систему описывают как колебательную с сосредоточенными (т.е. не зависящими от координат) параметрами массой т, коэффициентом упругости fe, сопротивлением [17]. [c.29]

    Кокс из масел имеет тонковолокнистую структуру Ку.р. этого кокса равен 16%. Кокс из асфальтенов, представляющих собою полициклические ароматические структуры с короткими алифатическими цепями, характеризуется округлыми порами и плотными межпоровыми стенками, Ку.р. такого кокса равен 8%. Силикагелевые смолы близки по своей молекулярной структуре к асфальтенам, но включают больше алифатических структур, чем асфальтены. Кокс из этих смол имеет структурные элементы, характерные в большей степени для кокса из асфальтенов и в меньшей степени для кокса из масел. Ку.р. кокса из силн-кагелевых смол практически равен коэффициенту упругого расширения кокса из исходного крекинг-остатка (11,5%). Добавка к исходному сырью масел и смол, выделенных из этого же сырья, увеличила степень волокнистости кокса (см. фото 8) и Ку.р. на 2—3%. [c.187]

    Для коксов различной плотности наименьшие значения коэффициента упругого расширения после снятия нагрузки /Су.р.), наивысшие значения коэффициента релаксации (/Срел.) и коэффициента прессовой добротности (/Сп. д.) наблюдаются после прокалки при следующих температурах (см. рис. 65— 69)  [c.233]

    Волокнистость структуры кокса приводит к повьппе-нию неравноосности зерен с повышением степени измельчения и в то же время к увеличению коэффициента упругого расширения. При крупном дроблении разрушение кокса, марки КНПЭ происходит прежде всего в местах структурных неоднородностей по макропорам и трещинам. Дпя кокса КНПЭ коэффициент термического расширения равен 1,6 10 1/°С, истираемость не более 13%. [c.90]

    Коэффициент упругого расширения находят следующим образом. Определенное количество кокса после размельчения до стандартных размеров частиц высыпают в специальную матрицу и прессуют. По достижении требуемого удельного давления замеряют высоту к спрессованного столбика кокса. Пспытаипе ири этом давлении продолжается 5 мин. Затем давление полностью снимают и снова замеряют высоту йг сирессоваиного столбика кокса. Коэффициент упругого расширения рассчитывают по формуле (в %)  [c.181]

    Коэффициент упругого расширения является показателем растрескиваемости электродов в эксплуатационных условиях. Известно, что при /Су.р не более 7—8% прессованныс изделия не растрескиваются при больших значениях этого коэффициента происходит расслоение изделия с образованием трещин. Поэтому, если требуется изготовление однородной эле тродиой продукции, то смешение коксов, значительно различающихся ио /(у.,,, ие допускается. [c.181]

    Для оценки поведения коксов при гидрорезке, хранении, транспортировании, дроблении и использовании в промышленности важно знать такие его свойства, как механическая прочность, коэффициент упругого расширения, коэффициенты релаксации и прочности частиц и нх изменения в процессе термообработки. [c.190]

    Упругость — это пропорциональность т и V, описываемая законом Гука X = Оу (рис. 3, а), при полной механической и термодинамической обратимости. Запасаемая в 1 см энергия составляет т /2С = Су /2. Символ ом-моделью упругости может служить пружина с коэффициентом упругости к = Р/х, численно равным модулю сдвига С. Следует, однако, помнить, что (в соответствии с двумя составляющими изменения свободной энергии системы = АЦ—ТАЗ) модуль С может иметь принципиально разную природу в случае истинной упругости, когда деформация тела связана с изменением межатомных расстояний, и в случае энтропийной эластичности, когда макродеформация обусловлена [c.309]

chem21.info

Элементы теории упругости | Мир сварки

 Введение

Под воздействием внешних сил всякое твердое тело изменяет свою форму – деформируется. Деформация, исчезающая с прекращением действия сил, называется упругой.

При упругой деформации тела возникают внутренние силы упругости, стремящиеся вернуть телу первоначальную форму. Величина этих сил пропорциональна деформации тела.

 Деформация растяжения и сжатия

Возникающее удлинение образца (Δl) под действием внешней силы (F) пропорционально величине действующей силы, первоначальной длине (l) и обратно пропорционально площади поперечного сечения (S) – закон Гука:

  Закон Гука 1)

где

1/E — коэффициент пропорциональности.

Величина E называется модулем упругости первого рода или модулем Юнга и характеризует упругие свойства материала. Величина F/S = p называется напряжением.

Деформация стержней любых длин и сечений (образцов) характеризуется величиной, называемой относительной продольной деформацией, ε = Δl/l.

Закон Гука для образцов любых форм:

  Закон Гука 2)

Модуль Юнга численно равен напряжению, увеличивающему длину образцов в два раза. Однако разрыв образца наступает при значительно меньших напряжениях. На рис.1 графически изображена экспериментальная зависимость p от ε, где pмакс – предел прочности, т.е. напряжение, при котором на стержне получается местное сужение (шейка), pтек – предел текучести, т.е. напряжение, при котором появляется текучесть (т.е. увеличение деформации без увеличения деформирующей силы), pупр – предел упругости, т.е. напряжение, ниже которого справедлив закон Гука (имеется в виду кратковременное действие силы).

Зависимость напряжения от относительной продольной деформацииРис.1. Зависимость напряжения от относительной продольной деформации:Кривая I относится к пластичному материалу, а кривая II – к хрупкому. Точки О характеризуют разрушение материала

Материалы разделяются на хрупкие и пластичные. Хрупкие вещества разрушаются при очень малых относительных удлинениях. Хрупкие материалы обычно выдерживают, не разрушаясь, большее сжатие, чем растяжение.

Совместно с деформацией растяжения наблюдается уменьшение диаметра образца. Если Δd – изменение диаметра образца, то ε1 = Δd/d принято называть относительной поперечной деформацией. Опыт показывает, что |ε1/ε|

Абсолютная величина μ = |ε1/ε| носит название коэффициент поперечной деформации или коэффициента Пуассона.

 Деформация сдвига

Сдвигом называют деформацию, при которой все слои тела, параллельные некоторой плоскости, смещаются друг относительно друга. При сдвиге объем деформируемого образца не меняется. Отрезок АА1 (рис.2), на который сместилась одна плоскость относительно другой, называют абсолютным сдвигом. При малых углах сдвига угол α ≈ tg α = АА1/AD характеризует относительную деформацию и его называют относительным сдвигом.

Деформация сдвигаРис.2. Деформация сдвига

Закон Гука для деформации сдвига может быть записан в виде

  Закон Гука для деформации сдвига 3)

где коэффициент G называется модуль сдвига.

 Сжимаемость вещества

Всестороннее сжатие тела приводит к уменьшению объема тела на ΔV и возникновению упругих сил, стремящихся вернуть телу первоначальный объем. Сжимаемостью (β) называется величина, численно равная относительному изменению объема тела ΔV/V при изменении действующего по нормали к поверхности напряжения (p) на единицу.

Величина, обратная сжимаемости, носит название модуля объемной упругости (K).

Изменение объема тела ΔV при всестороннем увеличении давления на ΔP вычисляется по формуле

  Изменение объема тела 4)

где

V — первоначальный объем тела.

 Соотношения между упругими постоянными

Модуль Юнга, коэффициент Пуассона, модуль объемной упругости и модуль сдвига связаны между собой уравнениями:

Модуль Юнга, коэффициент Пуассона

которые по двум известным упругим характеристикам позволяют, в первом приближении, рассчитать остальные.

Потенциальная энергия упругой деформации определяется по формуле

  Потенциальная энергия упругой деформации 5)

где

F — сила упругости;
Δl — величина деформации.

Единицы измерения модулей упругости: Н/м2 (СИ), дин/см2 (СГС), кгс/м2 (МКГСС) и кгс/мм2.

1 кгс/мм2 = 9,8·106 Н/м2 = 9,8·107 дин/см2 = 10-6 кгс/м2

 Приложение

Зависимость предела прочности от температурыРис.3. Зависимость предела прочности от температуры:1 – вольфрам, 2 – никелевая сталь, 3 – кобальтовая сталь, 4 – сталь N-155, 5 – Mo 0,5 Ti, 6 – Ti 36Al
Таблица 1 — Пределы прочности некоторых материалов (кГ/мм2)Материал Предел прочности при растяжении при сжатии
Аминопласты слоистые 8 20
Бакелит 2–3 8–10
Бетон — 0,5–3,5
Винипласт 4 8
Гетинакс 15–17 15–18
Гранит 0,3 15–26
Графит 0,5–1,0 1,6–3,8
Дуб (при 15% влажности) вдоль волокон 9,5 5
Дуб (при 15% влажности) поперек волокон — 1,5
Кирпич — 0,74–3
Латунь, бронза 22–50 —
Лед (0 °С) 0,1 0,1–0,2
Пенопласт плиточный 0,06 —
Полиакрилат (оргстекло) 5 7
Полистирол 4 10
Сосна (при 15% влажности) вдоль волокон 8 4
Сосна (при 15% влажности) поперек волокон — 0,5
Сталь для конструкций 38–42 —
Сталь кремнехромомарганцовистая 155 —
Сталь углеродистая 32–80 —
Сталь рельсовая 70–80 —
Текстолит ПТК 10 15–25
Фенопласт текстолитовый 8–10 10–26
Фторопласт-4 2 —
Целлон 4 16
Целлулоид 5–7 —
Чугун белый — до 175
Чугун серый мелкозернистый 21–25 до 140
Чугун серый обыкновенный 14–18 60–100
Таблица 2 — Модули упругости и коэффициенты ПуассонаНаименование материала Модуль ЮнгаE,107 Н/м2 Модуль сдвигаG,107 Н/м2 Коэффициент Пуассонаμ
Алюминий 6300–7000 2500–2600 0,32–0,36
Бетон 1500–4000 700–1700 0,1–0,15
Висмут 3200 1200 0,33
Бронза алюминиевая, литье 10300 4100 0,25
Бронза фосфористая катаная 11300 4100 0,32–0,35
Гранит, мрамор 3500–5000 1400–4400 0,1–0,15
Дюралюминий катаный 7000 2600 0,31
Известняк плотный 3500 1500 0,2
Инвар 13500 5500 0,25
Кадмий 5000 1900 0,3
Каучук 0,79 0,27 0,46
Кварцевая нить (плавленая) 7300 3100 0,17
Константан 16000 6100 0,33
Латунь корабельная катаная 9800 3600 0,36
Манганин 12300 4600 0,33
Медь прокатанная 10800 3900 0,31–0,34
Медь холоднотянутая 12700 4800 0,33
Никель 20400 7900 0,28
Плексиглас 525 148 0,35
Резина мягкая вулканизированная 0,15–0,5 0,05–0,15 0,46–0,49
Серебро 8270 3030 0,37
Стали легированные 20600 8000 0,25–0,30
Стали углеродистые 19500–20500 800 0,24–0,28
Стекло 4900–7800 1750–2900 0,2–0,3
Титан 11600 4400 0,32
Целлулоид 170–190 65 0,39
Цинк катаный 8200 3100 0,27
Чугун белый, серый 11300–11600 4400 0,23–0,27
Таблица 3 — Сжимаемость жидкостей при различных температурахВещество Температура,°С В интервале давлений,атм Сжимаемостьβ, 10-6 атм-1
Ацетон 14,2 9–36 111
0 100–500 82
0 500–1000 59
0 1000–1500 47
0 1500–2000 40
Бензол 16 8–37 90
20 99–296 78,7
20 296–494 67,5
Вода 20 1–2 46
Глицерин 14,8 1–10 22,1
Касторовое масло 14,8 1–10 47,2
Керосин 1 1–15 67,91
16,1 1–15 76,77
35,1 1–15 82,83
52,2 1–15 92,21
72,1 1–15 100,16
94 1–15 108,8
Кислота серная 0 1–16 302,5
Кислота уксусная 25 92,5 81,4
Керосин 10 1–5,25 74
100 1–5,25 132
Нитробензол 25 192 43,0
Оливковое масло 14,8 1–10 56,3
20,5 1–10 63,3
Парафин (с температурой плавления 55 °С) 64 20–100 83
100 20–400 24
185 20–400 137
Ртуть 20 1–10 3,91
Спирт этиловый 20 1–50 112
20 50–100 102
20 100–200 95
20 200–300 86
20 300–400 80
100 900–1000 73
Толуол 10 1–5,25 79
20 1–2 91,5

weldworld.ru

Коэффициент упругости — WiKi

В последовательном соединении имеется n{\displaystyle n}  пружин с жёсткостями k1,k2,...,kn.{\displaystyle k_{1},k_{2},...,k_{n}.}  Из закона Гука (F=−kl{\displaystyle F=-kl} , где l - удлинение) следует, что F=k⋅l.{\displaystyle F=k\cdot l.}  Сумма удлинений каждой пружины равна общему удлинению всего соединения l1+l2+...+ln=l.{\displaystyle l_{1}+l_{2}+...+l_{n}=l.} 

На каждую пружину действует одна и та же сила F.{\displaystyle F.}  Согласно закону Гука, F=l1⋅k1=l2⋅k2=...=ln⋅kn.{\displaystyle F=l_{1}\cdot k_{1}=l_{2}\cdot k_{2}=...=l_{n}\cdot k_{n}.}  Из предыдущих выражений выведем: l=F/k,l1=F/k1,l2=F/k2,...,ln=F/kn.{\displaystyle l=F/k,\quad l_{1}=F/k_{1},\quad l_{2}=F/k_{2},\quad ...,\quad l_{n}=F/k_{n}.}  Подставив эти выражения в (2) и разделив на F,{\displaystyle F,}  получаем 1/k=1/k1+1/k2+...+1/kn,{\displaystyle 1/k=1/k_{1}+1/k_{2}+...+1/k_{n},}  что и требовалось доказать.

ru-wiki.org

Коэффициент упругости — Википедия РУ

В последовательном соединении имеется n{\displaystyle n}  пружин с жёсткостями k1,k2,...,kn.{\displaystyle k_{1},k_{2},...,k_{n}.}  Из закона Гука (F=−kl{\displaystyle F=-kl} , где l - удлинение) следует, что F=k⋅l.{\displaystyle F=k\cdot l.}  Сумма удлинений каждой пружины равна общему удлинению всего соединения l1+l2+...+ln=l.{\displaystyle l_{1}+l_{2}+...+l_{n}=l.} 

На каждую пружину действует одна и та же сила F.{\displaystyle F.}  Согласно закону Гука, F=l1⋅k1=l2⋅k2=...=ln⋅kn.{\displaystyle F=l_{1}\cdot k_{1}=l_{2}\cdot k_{2}=...=l_{n}\cdot k_{n}.}  Из предыдущих выражений выведем: l=F/k,l1=F/k1,l2=F/k2,...,ln=F/kn.{\displaystyle l=F/k,\quad l_{1}=F/k_{1},\quad l_{2}=F/k_{2},\quad ...,\quad l_{n}=F/k_{n}.}  Подставив эти выражения в (2) и разделив на F,{\displaystyle F,}  получаем 1/k=1/k1+1/k2+...+1/kn,{\displaystyle 1/k=1/k_{1}+1/k_{2}+...+1/k_{n},}  что и требовалось доказать.

http-wikipediya.ru

Коэффициент Пуассона, формула и примеры

Определение и формула коэффициента Пуассона

Обратимся к рассмотрению деформации твердого тела. В рассматриваемом процессе происходит изменение размеров, объема и часто формы тела. Так, относительное продольное растяжение (сжатие) объекта происходит при его относительном поперечном сужении (расширении). При этом продольная деформация определена формулой:

    \[\varepsilon =\frac{l-l_0}{l_0}\left(1\right),\]

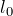где l_0 — длина образца до деформации, \Delta l=l-l_0 — изменение длины при нагрузке.

Однако, при растяжении (сжатии) происходит не только изменение длины образца, но и при этом меняются поперечные размеры тела. Деформация в поперечном направлении характеризуется величиной относительного поперечного сужения (расширения):

    \[{\varepsilon }_{\bot }=\frac{d-d_0}{d_0}\left(2\right),\]

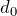где d_0 — диаметр цилиндрической части образца до деформации (поперечный размер образца).

Эмпирически получено, что при упругих деформациях выполняется равенство:

    \[{\varepsilon }_{\bot }=-\mu \varepsilon \left(4\right)\]

Коэффициент Пуассона в совокупности с модулем Юнга (E) является характеристикой упругих свойств материала.

Коэффициент Пуассона при объемной деформации

Если коэффициент объемной деформации ({\varepsilon }_V) принять равным:

    \[{\varepsilon }_V=\frac{\Delta V}{V_0}\left(5\right),\]

где \Delta V=V-V_0 — изменение объема тела, V_0 — первоначальный объем тела. То при упругих деформациях выполняется соотношение:

    \[{\varepsilon }_V={\left(1-\varepsilon \mu \right)}^2\left(1+\varepsilon \right)-1\left(6\right)\]

Часто в формуле (6) отбрасывают члены малых порядков и используют в виде:

    \[{\varepsilon }_V=\varepsilon \left(1-2\mu \right)\left(7\right)\]

Для изотропных материалов коэффициент Пуассона должен находиться в пределах:

    \[-1\le \mu \le 0,5\]

Существование отрицательных значений коэффициента Пуассона означает, что при растяжении поперечные размеры объекта могли бы увеличиваться. Это возможно при наличии физико-химических изменений в процессе деформации тела. Материалы, у которых коэффициент Пуассона меньше нуля называют ауксетиками.

Максимальная величина коэффициента Пуассона является характеристикой более эластичных материалов. Минимальное значение его относится к хрупким веществам. Так стали имеют коэффициент Пуассона от 0,27 до 0,32. Коэффициент Пуассона для резин варьируется в пределах: 0,4 — 0,5.

Коэффициент Пуассона и пластическая деформация

Выражение (4) выполняется и при пластических деформациях, однако в таком случае коэффициент Пуассона зависит от величины деформации:

    \[{\varepsilon }_{\bot }=-\mu (\varepsilon )\varepsilon \left(8\right)\]

С ростом деформации и возникновении существенных пластических деформаций 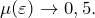\mu (\varepsilon )\to 0,5. Опытным путем установлено, что пластическая деформация происходит без изменения объема вещества, так как этот вид деформации возникает за счет сдвигов слоев материала.

Единицы измерения

Коэффициент Пуассона — это физическая величина, не имеющая размерности.

Примеры решения задач

ru.solverbook.com

Коэффициент Пуассона — WiKi

Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты.

Коэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

  Однородный стержень до и после приложения к нему растягивающих сил.

Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.

Пусть l{\displaystyle l}  и d{\displaystyle d}  длина и поперечный размер образца до деформации, а l′{\displaystyle l^{\prime }}  и d′{\displaystyle d^{\prime }}  — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l′−l){\displaystyle (l^{\prime }-l)} , а поперечным сжатием — величину, равную −(d′−d){\displaystyle -(d^{\prime }-d)} . Если (l′−l){\displaystyle (l^{\prime }-l)}  обозначить как Δl{\displaystyle \Delta l} , а (d′−d){\displaystyle (d^{\prime }-d)}  как Δd{\displaystyle \Delta d} , то относительное продольное удлинение будет равно величине Δll{\displaystyle {\frac {\Delta l}{l}}} , а относительное поперечное сжатие — величине −Δdd{\displaystyle -{\frac {\Delta d}{d}}} . Тогда в принятых обозначениях коэффициент Пуассона μ{\displaystyle \mu }  имеет вид:

μ=−ΔddlΔl.{\displaystyle \mu =-{\frac {\Delta d}{d}}{\frac {l}{\Delta l}}.} 

Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся Δll>0{\displaystyle {\frac {\Delta l}{l}}>0}  и Δdd<0{\displaystyle {\frac {\Delta d}{d}}<0} , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5.

Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.

К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы[2], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

ru-wiki.org