Содержание
Закон ламинарной фильтрации (закон Дарси).
Нужна помощь в написании работы?
Узнать стоимость
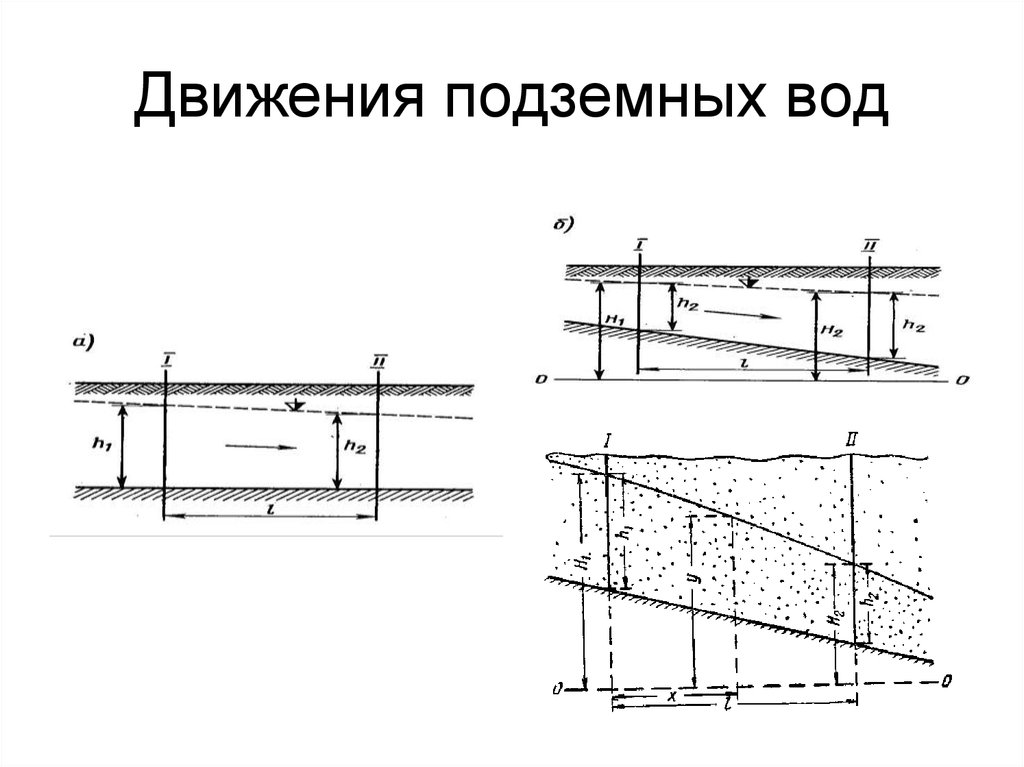
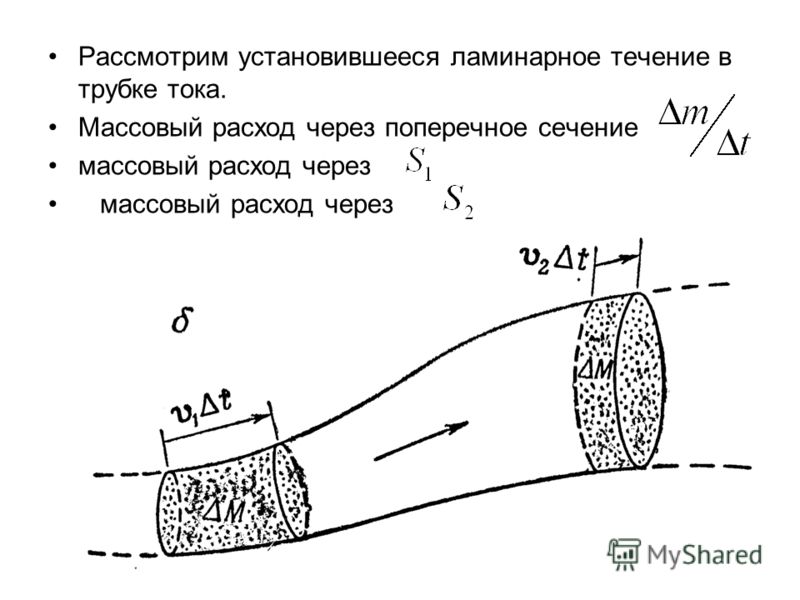
Закон ламинарной фильтрации Дарси устанавливает зависимость скорости фильтрации поровой воды от градиента гидравлического напора. Движение поровой воды называют фильтрацией, а связанные с этим процессы – фильтрационными.
В опытах Дарси измерял расход воды Q (м3) при фильтрации ее через цилиндр с песком площадью поперечного сечения А. Им получена следующая экспериментальная зависимость:
Q = k f ·i·A·t , (1)
где kf – коэффициент пропорциональности, названный коэффициентом фильтрации; t – время фильтрации.
Определим понятие скорости фильтрации ϑf (м/с) как расход поровой воды через единицу поперечного сечения в единицу времени. Тогда из экспериментальной зависимости Дарси будем иметь:
ϑf =k f
·i. (2)
Формула известна как закон ламинарной фильтрации Дарси, который можно сформулировать следующим образом: скорость фильтрации поровой воды прямо пропорциональна градиенту гидравлического напора.
Реальные грунты обладают начальным гидравлическим сопротивлением. Это означает, что фильтрационные процессы протекают лишь при гидравлических градиентах, больших определенной величины. Эту величину называют начальным гидравлическим градиентом i0. Величина начального гидравлического градиента, как и коэффициент фильтрации, зависит от вида грунта.
С учетом сделанного замечания запишем окончательное выражение для закона ламинарной фильтрации Дарси:
ϑf =k f
·(i- i0). (3)
Поможем написать любую работу на аналогичную
тему
Реферат
Закон ламинарной фильтрации (закон Дарси).
От 250 руб
Контрольная
работаЗакон ламинарной фильтрации (закон Дарси).
От 250 руб
Курсовая работа
Закон ламинарной фильтрации (закон Дарси).

От 700 руб
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Материалы 1
- Меню
Грунт, его определение и особенности свойств по сравнению с другими материалами.
Классификация по ГОСТ 25100-95 (Грунты. Классификация).
Составные части (фазы) грунта.
 Характеристики физических свойств.
Характеристики физических свойств.
Виды воды в грунтах. Свойства различных видов воды.
Связаная вода. Ее природа.
Влияние связаной воды на свойства грунта.
Газовая составляющая грунта. Ее влияние на свойства грунта.
Природа связанности грунта (сцепление между частицами).
Региональные (особые) виды грунтов и их основные свойства.

Материалы по теме:
Закон ламинарной фильтрации. Коэффициент фильтрации.
Шпаргалка
Добавить в избранное
(необходима авторизация)
|
КАТЕГОРИИ: Археология
ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы.
|
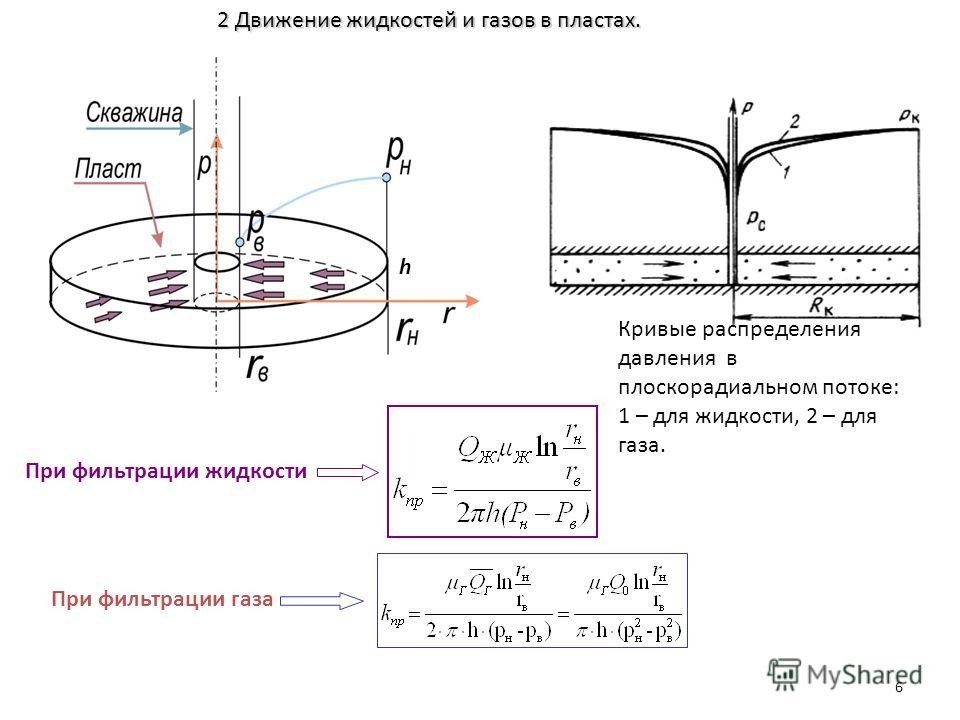
⇐ ПредыдущаяСтр 2 из 9Следующая ⇒ Водопроницаемость – способность грунтов пропускать ч/з себя оду или свойство водонасыщенного грунта под действием разности напоров пропускать ч/з свои поры сплошной поток воды. Закон фильтрации: скорость фильтрации Vф прямо пропорциональна гидравлическому напору i. Vф = Кф i , Кф – коэффициент фильтрации – это скорость движения грунтовых вод при i = 1 (см/сек; м/сут) Кф. песок= 10-2 10-3см/сек; Кф. глина= 10-8 10-12см/сек Водопроницаемость зависит от: — пористости грансостава; — градиента напора. В строительстве фильтрационные свойства грунта связаны: – с инженерными задачами (фильтрация берегов в результате строительства плотин). – с вопросами временного понижения уровня грунтовых вод для осушения котлованов. Закон звучит: скорость фильтрации Vf прямопропорц-на гидравлич-му коэ-ту i. Градиент напора i равен падению напора на единицу длины: Для пылевато-глинистых: скорость фильтрации прямо пропорциональна гидравлическому напору. Фильтрационные характеристики грунтов используются при: 1) Расчете дренажа; 2) Расчёте осадок сооружений (оснований) во времени; 3) Искусственном понижение у.г.в. 4) Расчете шпунтового ограждения при откопке котлованов, траншей; Эффективные и нейтральные давления. Полное давление — это все давление, приходящееся на водонасыщенный грунт. Эффективное давление — это часть полного давления, воспринимаемая твердыми минеральным частицами. Под действием этого давления всегда происходит уплотнение грунтов. Эффективным давление на скелет грунта называется потому, что оно повышает сопротивление грунта срезу. Нейтральное давление — давление, воспринимаемое поровой водой. Таким образом, эффективное и нейтральное давления составляют полное давление. Рz – эффективное давление (уплотняет и упрочняет грунт). Рw – нейтральное давление (создает напор в воде, вызывая ее фильтрацию). В любой момент времени в полностью водонасыщенной грунтовой массе имеет место соотношение: Р = Рz + Рw , где Р – полное давление При t = 0 Р = Рw При t = t1 Р = Рw+ Рz, При t = Р = Рz – это теоретически, практически для того чтобы Рw 0, требуется длительный период времени.
Методы опред-я коэф-та фильтр-и.
Сжимаемость грунтов. Компрессионная зависимость. Закон уплотнения. Сжимаемость грунтов – способность их уменьшаться в объеме (давать осадку) под действием внешнего давления. -одометре (приборе одноосного сжатия с жесткими боковыми стенками обоймы, в которую заключен образец грунта) называемым также компрессионным прибором; -стабилометре (приборе трехосного сжатия с эластичными боковыми стенками, в которые заключен грунт).
При относительно малых давлениях < сжимаемость грунта м.б. сравнительно небольшой, значительно меньшей, чем при больших давлениях. При изменении давления в практических целях заменяют зависимость между и прямолинейной, т.е. заменяют кривую на этом участке отрезком стягивающей хорды. Тогда из геометрических соображений получим , коэффициент сжимаемости . Для расчета осадок удобнее пользоваться коэффициентом относительной сжимаемости .Эти показатели необходимы для расчета осадок фундамента зданий или сооружений. Закон уплотнения Также можно сформулировать по-другому: изменение коэффициента пористости прямо пропорционально изменению давления. . 19. Структурная прочность грунта.Величина структурной прочности грунтов является весьма важной характеристикой грунтов. Величину ее можно определить по компрессионной кривой ненарушенной структуры, испытывая грунты (до достижения структурной прочности) весьма малыми ступенями нагрузки (примерно 0. Рисунок а) относ-е сжатие водонасыщенного грунта в зависимости от давления р, б) относ-е сжатие глинистого грунта при частичном разуплотнении в зависимости от давления Другой метод определения структурной прочности по результатам испытания бокового давления грунта при трехосной компрессии и соответствует давлению, при котором практически отсутствует боковое давление грунта. Определение указанных выше давлений требует разработки специальной методики испытания, и в настоящее время величина структурной прочности может быть определена лишь с известным приближением, зависящим, главным образом, от точности измерений.
20. Метод определения модуля деформации грунта по результатам штамповых испытаний. Штамповые испытания заключаются в том, что штамп — круглая плита — устанавливается на дно котлована на предварительно зачищенную и разровненную поверхность грунта, после чего загружается ступенями нагрузки. Последующая ступень нагрузки прикладывается после затухания осадки от предыдущей ступени. По линейному участку зависимости осадки , см, от нагрузки , МПа, устанавливается модуль деформации . Основным достоинством этого вида испытаний является то, что они ведутся непосредственно в грунтовом массиве. При испытаниях жесткими штампами требуется тщательная их установка на грунт с прилеганием по всей поверхности. Штамповые испытания производятся также в скважинах. В этом случае штамп устанавливается в забое скважины. Применяются также винтовые штампы.
21. Метод определения модуля деформации грунта по результатам прессиометрических испытаний. Прессиометр представляет собой закрытый цилиндр с резиновой боковой поверхностью в который подается давление и измеряется увеличение диаметра цилиндра (после стабилизации).
22. Метод статического зондирования.Зондированием грунта называется погружение в грунт конуса стандартного размера. Зондирование служит для оценки плотности песчаных грунтов и консистенции глинистых грунтов, выявления слабых прослоек грунта. При статическом зондировании измеряется усилие погружения (задавливания домкратом) конуса. В результате статического зондирования строятся графики зависимости удельного сопротивления погружению конуса с углом при вершине 60° в зависимости от глубины залегания грунтов, в которые он вдавливается.
23. Метод динамического зондирования.Зондированием грунта называется погружение в грунт конуса стандартного размера. Зондирование служит для оценки плотности песчаных грунтов и консистенции глинистых грунтов, выявления слабых прослоек грунта. При динамическом зондировании — количество ударов, необходимое для погружения конуса также на заданное расстояние по глубине. В результате динамического зондирования строятся графики зависимости количества ударов для погружения стандартного конуса (на 10 см) или пробоотборника в зависимости от залегания тех или иных пластов грунта. После проведения зондирования выявляются слабые слои грунтов основания и дается не только качественная, но и количественная оценка сопротивления грунтов внедрению конуса.
24.25.26. Сопротивление грунтов сдвигу. Методы опредления парамтров прочноти грунта. Закон Кулона для песчаных грунтов. Закон Кулона для связных грунтов. Сопротивление грунтов сдвигу определяет их прочность и устойчивость в основаниях сооружений и откосах, а также давления на ограждения котлованов. Сопротивление сдвигу по-разному проявляется в песчаных и глинистых грунтах и зависит от характера между частицами, слагающими грунт. Сопротивление грунта сдвигу может определяться различными методами: -метод прямого плоскостного среза; — -метод одноосного сжатия; — -метод трехосного сжатия; -метод лопостных испытаний; -метод шариковой пробы; Закон Кулона для песчаных грунтов имеет следующий вид: t = ×stgj Закон Кулона для связных грунтов имеет следующий вид: t = ×stgj + c . где — угол внутреннего трения. Угол внутреннего трения следует рассматривать как параметр линейного графика среза образца песчаного грунта, который проведен через начало координат. 27. Лопастное испытание грунтов на сдвиг. метод заключается в том, что лопастная крыльатка высотой h и диаметром d вдавливается в грунт, и вращением ее поверхности грунт срезается. Зная величину крутящего момента Мк соответствующего моменту среза грунта, вычисляем сопрот-е грунта сдвигу τS по ф-ле: τS=(2Мк)/(πd²h(1+d/3h). Рисунок
28. Испытания грунтов в стабилометре и приборе с независимо регулиуемыми главными напряжениями.Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств. Трехосному напряженному состоянию грунт подвергается в стабилометре.
29-30. Условие предельного равновесия : Условие предельного равновесия в главных напряжениях для сыпучего грунта: или для связного грунта: или 31.Определение показателей сжимаемости по результатам испытаний в стабилометре.Сложное напряженное состояние с помощью компрессионных испытаний оценить нельзя. Большую определенность дают трехосные испытания в стабилометрах. 32.Структурно-фазовая деформируемость грунтов. Общая зависимость между деформациями и напряжениями. Рисунок При любой нагрузке грунта, как правило наблюдаются и восстанавливающие и остаточные деформации грунта. 33. Принцип линейной деформируемости. Если зависимость между общими деформациями и напряжениями линейная, то для определения напряжений в грунтах полностью применимы уравнения теории упругости, для опделения же общих деформаций грунтов необходимы добавочные условия. Сформулированное положение носит название принцип линейной деформируемости грунтов. (При небольших изменених давления можно рассматривать грунт как линейно-деформируемое тела, т.е. с достаточной для практических целей точностью принимать зависимость между общими деформациями и напряжениями для них)-на этом положении базируется принцип линейной зависимости.
34. Определение напряжения в грунте от действия вертикальной сосредоточенной силы. 35. Определение напряжения в грунте от действия нескольких сосредоточенных сил. 36 Определение напряжения в грунте от действия произвольной в плане распределенной нагрузки. Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники со сторонами b и l и более сложные фигуры по контуру. С некоторым приближением давление, распределенное в пределах i-го прямоугольника , можно заменить равнодействующей Ni, приложенной в центре тяжести этого давления. Вертикальное сжимающее напряжение от действия силы Ni составит σzi= KiNi/z².
37. Определение напряжений в грунте по методу угловых точек под центром загруженной площадки.Метод угловых точек удобен для вычисления напряжений под центром равномерно загруженной площадки. На глубине z под центром площадки размерами lxb (l>b) напряжение равно сумме ответствующих угловых напряжений, создаваемых четырьмя площадками размерами l/2*b/2. Так, σя=Kop, где Ко=4Ку для площадки размерами и относительной вертикальной координаты β=2z/b. Значения коэф-в К приводятся в таблице
Метод угловых точек. Для определения вертикального напряжения σz в любой точке полупространства можно воспользоваться выражением σz =0,25άp. σz =σz1+σz2+σz3+σz4=0,25 (ά1+ά2+ά3+ά) p, где ά- коэффициенты принимаемые в зависимости от отношения сторон площадей загружения 1,2,3,4 и отношения z к ширине каждой из этих площадей. Так пользуясь методом угловых точек , можно найти напряжение σz в любой точке полупространства , к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади. 39.(Цытович с238)Распределение напряжений в грунте в случае плоской задачи! Задача о распределении напряжений в линейно-деформируемом массиве в ряде случаев упрощается ,если ее удается свести к плоской задаче,т.е. к такому напряженному состоянию ,когда напряжения распеределяються в одной плоскости и не зависят от координат ,перпендикулярных рассматриваемой плоскости. РИСУНОК.
40.Распределение давлений по под-е фунда-в,опир-ся на грунт(Цитович с253)Если фунд-т обладает жестк-ю(жестк-ть значительно отлич-ся от 0),то по подошве фунд-а должно происходить перераспределение напр-й с отклон-м от равномер-го.последнее особенно скажеться на распред-ии напр-й в сечениях массива наход-ся незначит-о от загр-й пов-и. ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
|
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
|
Понимание принципов ламинарного воздушного потока | Блог системного анализа
Автор
Каденс CFD
Ключевые выводы
Система ламинарного воздушного потока направлена на снижение турбулентности и поддержание однородности потока для уменьшения загрязнения.
Ламинарный режим воздушного потока может применяться для операций с нисходящим или поперечным потоком.
- Инструменты
CFD могут помочь в выявлении турбулентных областей и смягчении их с помощью точного моделирования.

Концепция ламинарного течения предполагает способность частиц жидкости двигаться по плавной траектории, при этом каждый слой движется параллельно другому. Эта концепция использовалась при разработке многих аэродинамических и гидродинамических систем, чтобы сделать их более эффективными за счет уменьшения сопротивления трения. Ламинарный поток воздуха следует точному принципу, согласно которому блоки обработки воздуха спроектированы так, чтобы демонстрировать однородность направления и скорости потока, а также обеспечивать постоянство.
Значение ламинарного воздушного потока проявляется в лабораториях или при производстве сложных полупроводников, где желательна стерильная рабочая среда. С помощью CFD-анализа можно эффективно моделировать такие системы с ламинарным потоком воздуха, включая камеры с нисходящим и поперечным потоком, туннели и рабочие места, при этом можно решить основные уравнения для прогнозирования скорости, давления и температуры, подходящих для создания стерильной среды. .
.
Ламинарный воздушный поток
Ламинарный поток воздуха относится к потоку в системе распределения воздуха, который следует принципу ламинарного потока воздуха. Когда молекулы газа движутся прямыми параллельными слоями, не пересекаясь и не смешиваясь друг с другом, образуются ламинарные условия. В замкнутом пространстве однородность скорости и направления за счет ламинарного потока воздуха дает возможность создать эффективную систему циркуляции. Циркуляция отфильтрованного воздуха в системе является ключом к поддержанию чистой и незагрязненной окружающей среды.
Этот тип системы ламинарного воздушного потока обычно используется в таких отраслях, как химическое производство или производство полупроводников, а также в медицинских и биологических лабораториях, где требуется однонаправленный поток чистого воздуха для максимальной защиты от внешних частиц. Большинство вентиляционных установок достигают этого, применяя вертикальный (нисходящий поток) или горизонтальный (поперечный поток) ламинарный режим воздушного потока.
Как работает система ламинарного воздушного потока?
Типичная компоновка системы воздушного потока включает закрытую камеру, рабочую станцию, систему фильтрации воздуха, освещение и вентилятор или воздуходувку. Вентилятор или воздуходувка всасывает воздух, который фильтруется через фильтрующую прокладку. Затем этот отфильтрованный воздух проходит через фильтр твердых частиц, который облегчает удаление микрозагрязнителей, таких как бактерии или пыль. Таким образом, стерильная рабочая среда может быть достигнута в рабочей зоне с равномерным потоком воздуха.
Вертикальный ламинарный поток воздуха: В системе с вертикальным ламинарным потоком воздуха фильтр расположен в верхней части шкафа, откуда комнатный воздух поступает в рабочую зону. Когда отфильтрованный воздух течет вертикально вниз к рабочей поверхности, загрязняющие вещества, включая бактерии или частицы, удаляются, создавая чистую рабочую среду.
Горизонтальный ламинарный поток воздуха: В системе с горизонтальным ламинарным потоком воздуха блок фильтрации расположен сбоку шкафа, откуда комнатный воздух поступает в рабочую зону. Затем отфильтрованный воздух течет горизонтально к рабочей поверхности, сметая загрязняющие вещества вместе с потоком.
Затем отфильтрованный воздух течет горизонтально к рабочей поверхности, сметая загрязняющие вещества вместе с потоком.
Анализ ламинарности с помощью инструментов CFD
Хотя ламинарность является целью систем воздушного потока, турбулентность может привести к загрязнению из-за отсутствия контроля потока. При проектировании систем ламинарного воздушного потока важно визуализировать ламинарность и любую нежелательную турбулентность. С помощью инструментов CFD можно анализировать диапазон чисел Рейнольдса в системе для проверки ламинарных и турбулентных условий. Любые области турбулентности, обнаруженные во время проектирования системы, могут быть устранены с помощью имитационной модели воздушного потока. В системе с ламинарным воздушным потоком анализ CFD также может помочь в расчете потерь давления, скорости и других характеристик воздушного потока с течением времени. Благодаря возможностям создания сетки и моделирования на платформах CFD, таких как Pointwise и Omnis, можно добиться желаемой ламинарности в конструкции системы воздушного потока.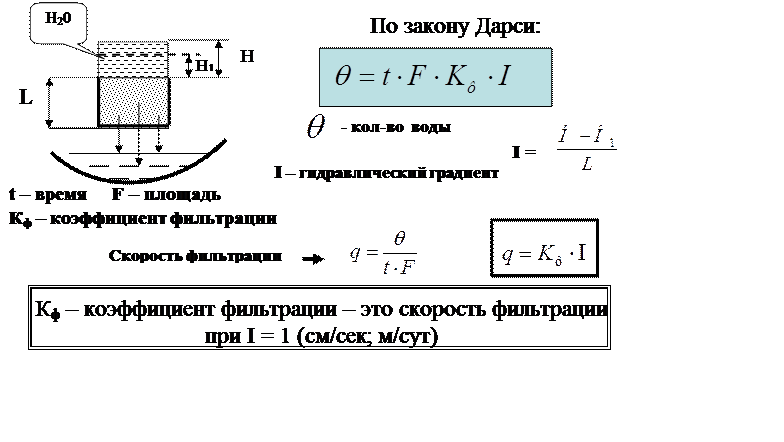
Подпишитесь на нашу рассылку, чтобы получать последние обновления CFD, или просмотрите пакет программного обеспечения Cadence для CFD, включая Omnis и Pointwise, чтобы узнать больше о том, какое решение у Cadence есть для вас.
Программное обеспечение CFD Подпишитесь на нашу рассылку новостей
Доступ к электронной книге
4.4 Закон Дарси – Дождь или светит солнце
В 1856 г. французский инженер Генри Дарси (рис. 4-4), работавший над системами фильтрации воды, доказал, что поток воды через песчаные пласты пропорционален гидравлическому градиенту, то же самое соотношение обнаружил Пуазей для ламинарного течения через трубы [4]. . Константа пропорциональности, K , называется гидравлической проводимостью и является мерой способности материала пропускать воду. Открытие Дарси получило название закона Дарси и может быть записано как:
.
(уравнение 4-3)
где Δψ t – разность полного водного потенциала между двумя точками в насыщенной пористой среде, разделенными расстоянием L . Символ K s служит для пояснения того, что мы имеем в виду насыщенную гидравлическую проводимость почвы, которая резко отличается от гидравлической проводимости ненасыщенной почвы, как мы вскоре увидим. Дарси отметил, что гидравлическая проводимость зависит от проницаемости пористой среды. Сравнивая закон Дарси с законом Пуазейля, мы также видим, что гидравлическая проводимость зависит от вязкости жидкости, которая сама зависит от температуры жидкости. Хотя в экспериментах, приведших к закону Дарси, использовался только песок, доказано, что это соотношение точно описывает поток в самых разных типах почв и других пористых средах. Оно стало одним из важнейших соотношений в физике почв, гидрологии и гидрогеологии. Пожалуйста, возьмите карандаш и бумагу и посмотрите следующие два видео, чтобы узнать, как использовать закон Дарси для оценки потока воды через столбы насыщенной почвы. В первом видео показан пример потока через горизонтальный столб почвы, а во втором видео показан пример потока через вертикальный столб почвы.
Символ K s служит для пояснения того, что мы имеем в виду насыщенную гидравлическую проводимость почвы, которая резко отличается от гидравлической проводимости ненасыщенной почвы, как мы вскоре увидим. Дарси отметил, что гидравлическая проводимость зависит от проницаемости пористой среды. Сравнивая закон Дарси с законом Пуазейля, мы также видим, что гидравлическая проводимость зависит от вязкости жидкости, которая сама зависит от температуры жидкости. Хотя в экспериментах, приведших к закону Дарси, использовался только песок, доказано, что это соотношение точно описывает поток в самых разных типах почв и других пористых средах. Оно стало одним из важнейших соотношений в физике почв, гидрологии и гидрогеологии. Пожалуйста, возьмите карандаш и бумагу и посмотрите следующие два видео, чтобы узнать, как использовать закон Дарси для оценки потока воды через столбы насыщенной почвы. В первом видео показан пример потока через горизонтальный столб почвы, а во втором видео показан пример потока через вертикальный столб почвы. При необходимости ставьте видео на паузу и решайте задачи самостоятельно, чтобы улучшить свое понимание.
При необходимости ставьте видео на паузу и решайте задачи самостоятельно, чтобы улучшить свое понимание.
Рис. 4‑4. Портрет Генри Дарси работы Ф. Перродена из собрания Муниципальной библиотеки Дижона. Всеобщее достояние.
Если для закона Пуазейля требовалась конкретная информация о геометрии потока, т. е. радиус трубы, то для закона Дарси требуется только эмпирически определенная константа — гидравлическая проводимость. Это дает закону Дарси гибкость, применимую практически к любой пористой среде, если поток является ламинарным. Но за эту гибкость приходится платить; гидравлическая проводимость может отличаться на несколько порядков от одного типа грунта к другому. Гидравлическая проводимость также может отличаться на порядок или более от одного образца к другому в пределах одного и того же типа грунта. Чтобы лучше понять причины этой огромной изменчивости, давайте рассмотрим некоторые из основных факторов, влияющих на гидравлическую проводимость и скорость потока почвенной воды.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления


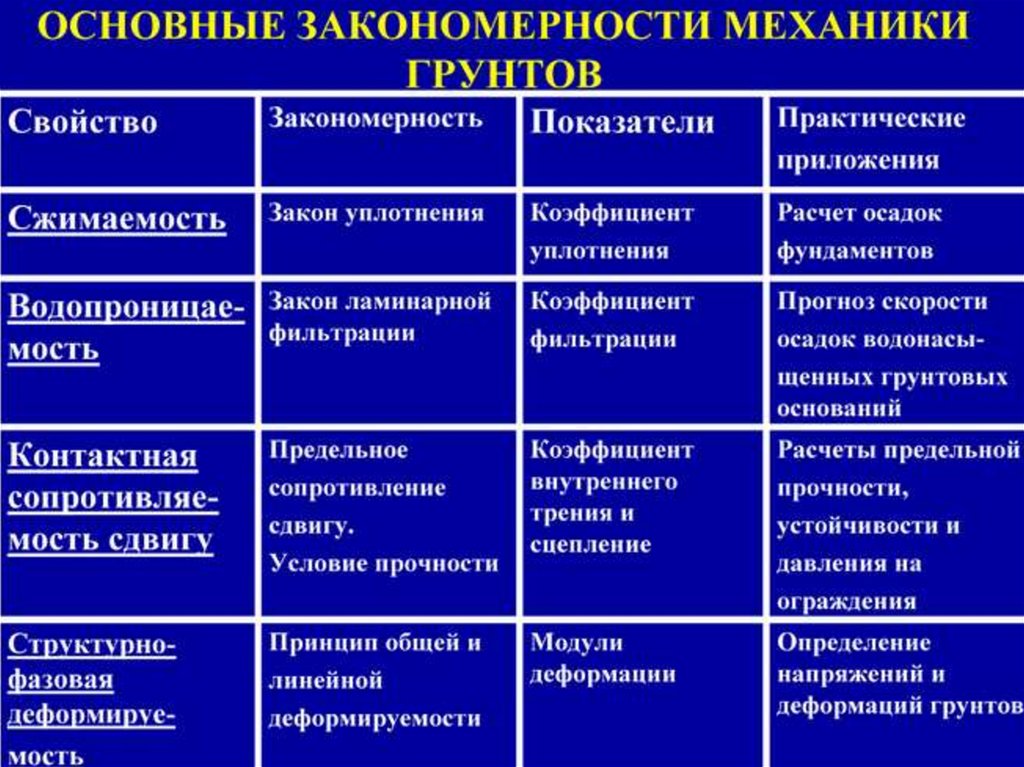
 Степень сжимаемости грунтов зависит от структуры грунта и является важной характеристикой механических свойств грунта, которая используется для расчета осадок зданий и различных сооружений. Сжимаемость грунтов обусловлена изменением их пористости при приложении нагрузки и происходит за счет возникновения взаимных сдвигов частиц. Уменьшения толщины водно-коллоидных пленок отжатия воды в водонасыщенных грунтах и за счет разрушения кристаллизационных связей в сильно структуированных грунтах. В связи с тем, что сжимаемость грунтов связана с уменьшением их пористости, в механике грунтов принято характеризовать сжимаемость грунта зависимостью коэффициента пористости от уплотняющего давления . Эта зависимость называется компрессионной и определяется в лабораторных условиях экспериментально в приборах двух типов:
Степень сжимаемости грунтов зависит от структуры грунта и является важной характеристикой механических свойств грунта, которая используется для расчета осадок зданий и различных сооружений. Сжимаемость грунтов обусловлена изменением их пористости при приложении нагрузки и происходит за счет возникновения взаимных сдвигов частиц. Уменьшения толщины водно-коллоидных пленок отжатия воды в водонасыщенных грунтах и за счет разрушения кристаллизационных связей в сильно структуированных грунтах. В связи с тем, что сжимаемость грунтов связана с уменьшением их пористости, в механике грунтов принято характеризовать сжимаемость грунта зависимостью коэффициента пористости от уплотняющего давления . Эта зависимость называется компрессионной и определяется в лабораторных условиях экспериментально в приборах двух типов:
 002-0.010 МПа), тогда резкий перелом компрессионной кривой и будет соответствовать структурной прочности сжатия грунта. Значение давления, соответствующее точке пересечения кривой с осью давления равно значению структурной прочности на сжатие .
002-0.010 МПа), тогда резкий перелом компрессионной кривой и будет соответствовать структурной прочности сжатия грунта. Значение давления, соответствующее точке пересечения кривой с осью давления равно значению структурной прочности на сжатие .
 По отношению / устанавливается по линейному участку диаграммы величина модуля деформации . В обычных случаях для вычисления нужно знать коэффициент Пуассона грунта. Мы получаем при этом испытании модуль деформации в горизонтальном, а не в вертикальном направлении, в то время как в грунтах, являющихся природными образованиями, деформируемость в горизонтальном и вертикальном направлениях может быть разной (проявляется анизотропия).
По отношению / устанавливается по линейному участку диаграммы величина модуля деформации . В обычных случаях для вычисления нужно знать коэффициент Пуассона грунта. Мы получаем при этом испытании модуль деформации в горизонтальном, а не в вертикальном направлении, в то время как в грунтах, являющихся природными образованиями, деформируемость в горизонтальном и вертикальном направлениях может быть разной (проявляется анизотропия). При этом боковое сопротивление погружению штанги, на которую насажен конус, исключается. После проведения зондирования выявляются слабые слои грунтов основания и дается не только качественная, но и количественная оценка сопротивления грунтов внедрению конуса Рисунок. Интерпретация результатов зондирования по глубине, м
При этом боковое сопротивление погружению штанги, на которую насажен конус, исключается. После проведения зондирования выявляются слабые слои грунтов основания и дается не только качественная, но и количественная оценка сопротивления грунтов внедрению конуса Рисунок. Интерпретация результатов зондирования по глубине, м Рисунок. Интерпретация результатов зондирования по глубине
Рисунок. Интерпретация результатов зондирования по глубине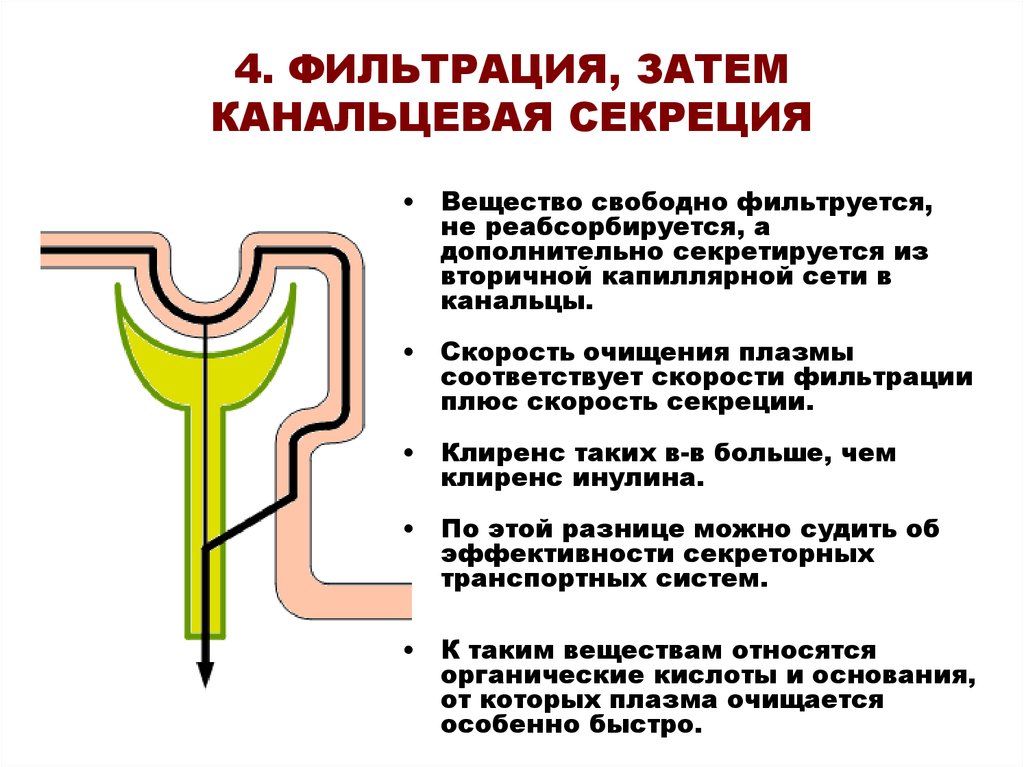 Рисунок. Результирующая схема испытания прямым срезом: а — песчаный грунт; б — глинистый грунт
Рисунок. Результирующая схема испытания прямым срезом: а — песчаный грунт; б — глинистый грунт В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта где — изменение объема образца.В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.
В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта где — изменение объема образца.В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее. Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств. Трехосному напряженному состоянию грунт подвергается в стабилометре.В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта где — изменение объема образца. В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее.
Испытание грунта в приборе трехосного сжатия ближе отвечает его работе в природных условиях и даёт наиболее надёжные результаты в определении его прочностных и деформационных свойств. Трехосному напряженному состоянию грунт подвергается в стабилометре.В приборе грунт находится в условиях объёмного напряженного состояния. Особенностью таких испытаний в стабилометрах является равномерное боковое сжатие образца, т.е. равенство боковых главных напряжений. Для наблюдениея за деформировнием образца стенки камеры обычно изготавливаются из прозрачного материала. Оценка сжимаемости грунтов в приборах трехосного сжатия производится по объемной деформации грунта где — изменение объема образца. В стабилометрах изменение объема образца определяется по объему жидкости, поступающей в камеру прибора или входящей из нее. Зависимость в общем случае будет криволинейной, особенно если рассматривать деформации в большом диапазоне. Криволинейная зависимость между общими относительными деформациями е и напряжениями σ достаточно хорошо можно апроксимировать степенным законом. е=ασm
Зависимость в общем случае будет криволинейной, особенно если рассматривать деформации в большом диапазоне. Криволинейная зависимость между общими относительными деформациями е и напряжениями σ достаточно хорошо можно апроксимировать степенным законом. е=ασm От действия силы N во всех точках полупространства возникает сложное напряженное состояние. Пусть положение точки М1 определяется полярными координатами R и β системы координат с началом в точке приложения силы N. Под действием силы N точка М1 переместиться в направлении радиуса R на величину s1. Чем дальше от точки О будет расположена точка М1 , тем меньше будет ее перемещение ; при R=бесконечности перемещение точки М1будет =0.Следовательно S1 можно принять обратно пропорциональным R. В то же время при одном и том же значении R для различных величин угла β перемещения точек будут неодинаковы. Наибольшее перемещение получит точка , расположенная на оси z , т.е. при β=0. С увеличением угла β перемещения по направлению радиуса R уменьшаются , и в случае β=90 град. При малых деформациях будут =0.В связи с этим можно принять , что перемещение точки М1 по направлению радиуса , кроме зоны около точки приложения силы N, будет S1=(ά1/R )cosβ, где ά1-коэфф. пропорциональности. Эта зависимость удовлетворяет граничным условиям.
От действия силы N во всех точках полупространства возникает сложное напряженное состояние. Пусть положение точки М1 определяется полярными координатами R и β системы координат с началом в точке приложения силы N. Под действием силы N точка М1 переместиться в направлении радиуса R на величину s1. Чем дальше от точки О будет расположена точка М1 , тем меньше будет ее перемещение ; при R=бесконечности перемещение точки М1будет =0.Следовательно S1 можно принять обратно пропорциональным R. В то же время при одном и том же значении R для различных величин угла β перемещения точек будут неодинаковы. Наибольшее перемещение получит точка , расположенная на оси z , т.е. при β=0. С увеличением угла β перемещения по направлению радиуса R уменьшаются , и в случае β=90 град. При малых деформациях будут =0.В связи с этим можно принять , что перемещение точки М1 по направлению радиуса , кроме зоны около точки приложения силы N, будет S1=(ά1/R )cosβ, где ά1-коэфф. пропорциональности. Эта зависимость удовлетворяет граничным условиям.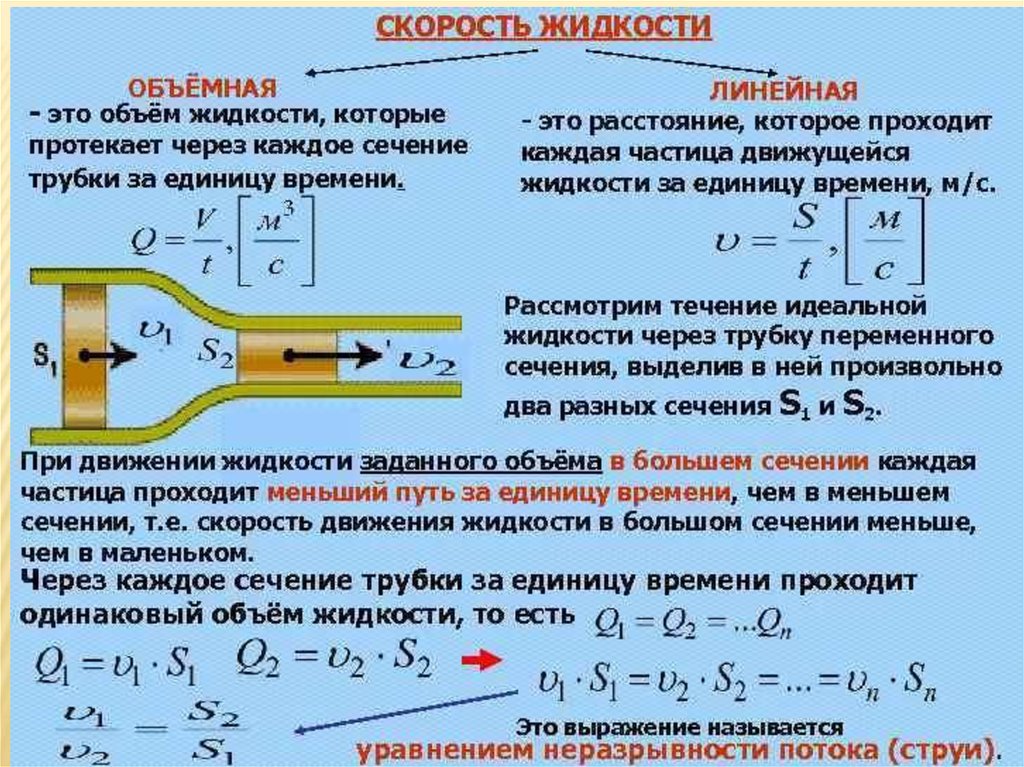 Рассм. теперь точку М2 на продолжении радиуса R. Пусть точка М2 находиться на расстоянии dR от точки М1.Руководствуясь записанным выражением , найдем перемещение точки М2 по направлению радиуса R: S2=[ά1/(R+dR)]/cosβ. Ком случае относительная деформация грунта на отрезке dR составит .Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки , перпендикулярные направлению радиуса R, без учета силы тяжести грунта : , где ά2- коэфф. пропорциональности между напряжениями и деформациями . Учитывая, что R²=r²+z² ,будем иметь , где Аналогично могут быть найдены остальные компоненты напряжения в точке М1.Подставляя в последнюю формулу значение коэфф. К найденного по таблице определяют вертикальное сжимающее напряжение σz, развивающееся в грунтах при действии сосредоточенной стлы.
Рассм. теперь точку М2 на продолжении радиуса R. Пусть точка М2 находиться на расстоянии dR от точки М1.Руководствуясь записанным выражением , найдем перемещение точки М2 по направлению радиуса R: S2=[ά1/(R+dR)]/cosβ. Ком случае относительная деформация грунта на отрезке dR составит .Пренебрегая величиной RdR, малой по сравнению с R², и учитывая линейную зависимость между напряжениями и деформациями, найдем выражение для напряжений сжатия, действующих на площадки , перпендикулярные направлению радиуса R, без учета силы тяжести грунта : , где ά2- коэфф. пропорциональности между напряжениями и деформациями . Учитывая, что R²=r²+z² ,будем иметь , где Аналогично могут быть найдены остальные компоненты напряжения в точке М1.Подставляя в последнюю формулу значение коэфф. К найденного по таблице определяют вертикальное сжимающее напряжение σz, развивающееся в грунтах при действии сосредоточенной стлы. Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил(N1,N2,…..Nn), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σz в любой точке М простым суммированием: σz= K1N1/z²+K2N2/z²+……+KnNn/z². Значение коэффициенте К определяют по таблицам в зависимости от отношений r1/z,r2/z,….., rn/z.
Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил(N1,N2,…..Nn), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σz в любой точке М простым суммированием: σz= K1N1/z²+K2N2/z²+……+KnNn/z². Значение коэффициенте К определяют по таблицам в зависимости от отношений r1/z,r2/z,….., rn/z.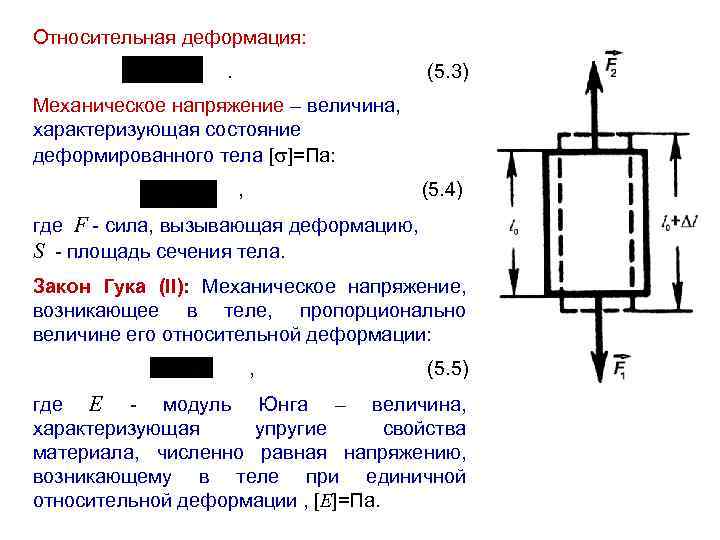 Определив величину σzi от нагрузки каждой из небольших фигур , на которые разбита площадь А, и произведя суммирование этих напряжений , определим напряжение σz от действия распределенной местной нагрузки : σz= Σ KiNi/z² Точность расчета увеличивается с уменьшением b и l
Определив величину σzi от нагрузки каждой из небольших фигур , на которые разбита площадь А, и произведя суммирование этих напряжений , определим напряжение σz от действия распределенной местной нагрузки : σz= Σ KiNi/z² Точность расчета увеличивается с уменьшением b и l Если проекция рассм. точки М´ на горизонтальную поверхность полупространства располагается в пределах площади загружения , то эту площадь можно разбить на 4 прямоугольника так , чтобы точка М была угловой точкой каждого из них . Тогда напряжение σz найдем суммированием напряжений под угловыми точками 4 площадей загружения:
Если проекция рассм. точки М´ на горизонтальную поверхность полупространства располагается в пределах площади загружения , то эту площадь можно разбить на 4 прямоугольника так , чтобы точка М была угловой точкой каждого из них . Тогда напряжение σz найдем суммированием напряжений под угловыми точками 4 площадей загружения: Этот случай соответствует напр сост-ю под лент-ыми фунд-и,подпорными стенками,насыпями и подобными сооруж-и.Длина этих сооружений значительно превосходит их поперечные размеры,когда в любом месте,можно двумя параллельными сечениями выделить часть сооружения,распределение напряжений под которой будет характеризовать напряженное состояние под всем сооружением.При этом предпологается что в направлении перпенд-м рассматрив-й плоск-и нагрузка не меняется.Важное св-во плоск-й задачи в том:составляющие напр-й σy, σz,τ в расматрив-й плоск-и ZOY не зависят от деф-ых характер-к линейно-деф-го полупростр-а:модуля деформацииE0 и коэф-а поперечного расшерения..
Этот случай соответствует напр сост-ю под лент-ыми фунд-и,подпорными стенками,насыпями и подобными сооруж-и.Длина этих сооружений значительно превосходит их поперечные размеры,когда в любом месте,можно двумя параллельными сечениями выделить часть сооружения,распределение напряжений под которой будет характеризовать напряженное состояние под всем сооружением.При этом предпологается что в направлении перпенд-м рассматрив-й плоск-и нагрузка не меняется.Важное св-во плоск-й задачи в том:составляющие напр-й σy, σz,τ в расматрив-й плоск-и ZOY не зависят от деф-ых характер-к линейно-деф-го полупростр-а:модуля деформацииE0 и коэф-а поперечного расшерения.. Согласно принципу Сен-Венана,распр-е напр-й будет завис-ть только от полож-я равнодей-й внешней нагр-и.Распределение реактив-х давл-й по под-е фунд-в со знач-и размерами в плане имеет огромн-е практич-е знач-е.зная реак-е давл-я и внеш-е силы,по ур-м статики легко опр-ся изгиб-е мом-ы и перерезв-е силы,по велечине кот-х и расчит-ся фунд-ы.
Согласно принципу Сен-Венана,распр-е напр-й будет завис-ть только от полож-я равнодей-й внешней нагр-и.Распределение реактив-х давл-й по под-е фунд-в со знач-и размерами в плане имеет огромн-е практич-е знач-е.зная реак-е давл-я и внеш-е силы,по ур-м статики легко опр-ся изгиб-е мом-ы и перерезв-е силы,по велечине кот-х и расчит-ся фунд-ы. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.005 с.)