Содержание
Пористость грунта — sprosigeologa.ru
пористость грунтаПористость грунта – это совокупный объем закрытых и открытых пор в единице его объёма. Она определяется по формуле:
n=1–m=1–ρd/ρs=е/(1+е), где
m – объём минеральной части грунта; ρd – плотность скелета грунта; ρs – плотность минеральных частиц; е – коэффициент пористости.
Таким образом, для ее определения достаточно иметь значения плотности и плотности частиц.
Пористость грунтов формируется в процессе их образования и постдиагенетических преобразований, связанных с развитием трещин, выветриванием, выщелачиванием и с различными геохимическими процессами. У обломочных и глинистых грунтов она существенно зависит от степени дисперсности и литификации, формы частиц, типа цемента, плотности сложения, глубины залегания от поверхности Земли или в пределах геологической структуры.
Этот параметр определяет многие свойства грунтов: влажность, влагоёмкость, капиллярность, водопроницаемость, деформируемость и прочность.
Ее высокие значения свойственны для песчано-глинистых грунтов (до 80 %). Осадочные и вулканогенные породы (известняки, лавы, туфы и др.) характеризуются большим диапазоном ее значений (от 10 % и менее до 50 %), в отличие от магматических и метаморфических (0,1 – 3 %).
Разновидности пор
По величине пор выделяются следующие разновидности: мелкопористые – составляют сотые и тысячные доли мм; и крупнопористые материалы – от десятых долей мм до 2 мм.
Поры в грунтах по величине принято делить на субкапиллярные (менее 0,2 мк), капиллярные (0,2-100 мк), сверхкапиллярные (более 100 мк).
Различают пористость общую (абсолютную, физическую, полную), открытую и закрытую. Общая – это совокупность всех пор, заключенных в грунте; открытая п. – это объём связанных между собой пор. Закрытая п. – это совокупность замкнутых, взаимно не сообщающихся пор. В нефтяной геологии выделяют эффективную п., представленную совокупностью пор, занятых нефтью, газом, и динамическую п. – выраженную объёмом пор, через который при определённом давлении и температуре происходит движение насыщающих жидкостей или газов.
Определение пористости
В лабораторных условиях, помимо расчетного, пористость определяется методами свободного вакуумного и принудительного (под давлением) насыщения грунтов жидкостью, а также методами, основанными на расширении газа, и др. В поле применяют различные виды каротажа скважин. В геологии результаты ее изучения используют для оценки запасов нефти, воды, газа, выбора технологии их разработки и др.
Значения пористости горных пород
Значение пористости нескальных грунтов
Наименование горной породы | Пористость, % | Коэф. пористости |
Гравий | 25-30 | 0,25-0,30 |
Песок | 30-40 | 0,30-0,40 |
Супесь | 40-45 | 0,40-0,45 |
Суглинок | 45-50 | 0,45-0,50 |
Глина | 50-65 | 0,50-0,65 |
Значение пористости полускальных и скальных грунтов
Грунт | Пористость, % | Грунт | Пористость, % |
Алевролит | 14-30 | Кварцит | 4,8-8,8 |
Базальт | 3,0-6,0 | Липарит | 4. |
Габбро | 0,02-1,5 | Мрамор | 0,1-1,0 |
Гранит | 0,06-2,0 | Опока | 39-49 |
Гранодиорит | 0,2-5,0 | Периодотит | 0,02-2,0 |
Диабаз | 0,08-4,5 | Сиенит | 0,1-3,5 |
Диорит | 0,1-3,5 | Пироксенит | 0,1-1,0 |
Доломит крепкий | 3. | Порфирит | 0,4-4,3 |
Известняк: крепкий слабый |
5,0-13,7 10,0-22,0 | Песчаник: крепкий слабый |
1,6-10,0 16,0-26,0 |
Кварцевый порфирит | 0,5-3,5 | Трахит | 3,0-8,0 |
Главная—>Определение свойств грунтов—>Пористость грунта
Определение коэффициента пористости и степень влажности глинистого грунта.
ИГЭ-3.
Дано: глина полутвердая,
плотность частиц грунта s
= 2,78 т/м3;
плотность грунта
= 2,0 т/м3;
влажность грунта W
= 20 % = 0,2; плотность воды w=1 т/м3.
Решение: Коэффициент
пористости грунта определяется по
формуле
е =
Sr
==
Данный грунт
непросадочный,
т.к. Sr
= 0,832 > 0,8
ИГЭ-4.
Дано: суглинок
полутвёрдый, плотность частиц грунта
s
= 2,66 т/м3;
плотность грунта
= 1,91 т/м3;
влажность грунта W
= 21 % = 0,21; плотность воды w=1 т/м3.
Решение: Коэффициент
пористости грунта определяется по
формуле
е =
Sr
==
Данный грунт не
просадочный,
т.к. Sr
= 0,815 > 0,8
Определение показателя просадочности Iss грунта – не требуется, т.К. Грунты не просадочные. Определение удельного веса грунта во взвешенном состоянии
ИГЭ-1.
Дано: коэффициент
пористости грунта e
= 0,667; удельный вес воды γW
= 10 кН/м3;
удельный вес грунта γS
= 26,5 кН/м3
Решение:
кН/м3
ИГЭ-3.
Дано: коэффициент
пористости грунта e
= 0,668; удельный вес воды γW
= 10 кН/м3;
удельный вес грунта γS
= 27,8 кН/м3
Решение:
кН/м3
ИГЭ-4.
Дано: коэффициент
пористости грунта e
= 0,685; удельный вес воды γW
= 10 кН/м3;
удельный вес грунта γS
= 26,6 кН/м3
Решение:
кН/м3
ИГЭ-5.
Дано: коэффициент
пористости грунта e
= 0,532; удельный вес воды γW
= 10 кН/м3;
удельный вес грунта γS
= 26,6 кН/м3
Решение:
кН/м3
Определение плотности грунта в сухом состоянии.
ИГЭ-1.
Дано: плотность грунта
0
= 1,86 т/м3;
природная влажность W
= 0,17
Решение: плотность
грунта в сухом состоянии d
определяется по формуле
d
=
=
т/м3
ИГЭ-2.
Дано: плотность грунта
0
= 0,77 т/м3;
природная влажность W
= 7,8
Решение: плотность
грунта в сухом состоянии d
определяется по формуле
d
=
=
т/м3
ИГЭ-3.
Дано: плотность грунта
0
= 2,0 т/м3;
природная влажность W
= 0,2
Решение: плотность
грунта в сухом состоянии d
определяется по формуле
d
=
=
т/м3
ИГЭ-4.
Дано: плотность грунта
0
= 1,91 т/м3;
природная влажность W
= 0,21
Решение: плотность
грунта в сухом состоянии d
определяется по формуле
d
=
=
т/м3
ИГЭ-5.
Дано: плотность грунта
0
= 1,98 т/м3;
природная влажность W
= 0,14
Решение: плотность
грунта в сухом состоянии d
определяется по формуле
d
=
=
т/м3
Определение механических свойств грунтов.
 Определение коэффициента относительной сжимаемости mv.
Определение коэффициента относительной сжимаемости mv.
ИГЭ-1.
Дано: песок,
модуль деформации Е0
= 10 МПа;
= 0,8; e
= 0,667
Решение:
коэффициент относительной сжимаемости
определим по формуле
mv
=
МПа среднесжимаемый грунт
ИГЭ-3.
Дано: глина,
модуль деформации Е0
= 18 МПа;
= 0,4; e
= 0,668
Решение:
коэффициент относительной сжимаемости
определим по формуле
mv
=
МПа малосжимаемый грунт
ИГЭ-4.
Дано: суглинок,
модуль деформации Е0
= 13 МПа;
= 0,5; e
= 0,685
Решение:
коэффициент относительной сжимаемости
определим по формуле
mv
=
МПа среднесжимаемый грунт
ИГЭ-5.
Дано: песок,
модуль деформации Е0
= 30 МПа;
= 0,8; e
= 0,532
Решение:
коэффициент относительной сжимаемости
определим по формуле
mv
=
МПа малосжимаемый грунт
Сводная таблица
характеристик грунтов
Номер инж- геол. | Глубина подошвы | Наименование | Физические | Механические | |||||||||||||||
основные | Дополни-тельные | производные | индексационные | деформа-ционные | прочност-ные | ||||||||||||||
ρs, т/м3 | ρ2, т/м3 | W, % | WL, % | WP, % | ρd, т/м3 | e, — | γвзв, кН/м3 | IP, % | IL, — | Sr, — | ISS, — | mV, 1/МПа | E0, МПа | φ, град. | c0, кПа | R0, кПа | |||
1. | 3,0 | Насыпной | 2,65 | 1,86 | 17 | — | — | 1,59 | 0,667 | 9,89 | — | — | 0,675 | — | 0,067 | 20 | 35 | 1 | 400 |
2. | 2,0 | Торф | 1,5 | 0,77 | 780 | — | — | 0,087 | — | — | — | — | — | — | — | 1 | 10 | 6 | — |
3. | 5,0 | Глина | 2,78 | 2,0 | 20 | 34 | 16 | 1,67 | 0,668 | 10,67 | 0,18 | 0,222 | 0,832 | 0,166 | 0,044 | 15 | 19 | 29 | 500 |
4. | 6,0 | Суглинок | 2,66 | 1,91 | 21 | 34 | 20 | 1,58 | 0,685 | 9,85 | 0,14 | 0,071 | 0,815 | 0,13 | 0,065 | 13 | 32 | 6 | 250 |
5. | 4,0 | Песок | 2,66 | 1,98 | 14 | — | — | 1,74 | 0,532 | 10,83 | — | — | 0,7 | — | 0,041 | 30 | 38 | 2 | 500 |
Все грунты, кроме
торфа, могут служить естественным
основанием для фундамента.
Пористость почвы — Geotechdata.info
Geotechdata.info — Обновлено
18.11.2013
Пористость грунта (n) – отношение объема пустот к общему объему грунта:
n = (V_v) / V
Где V_v – объем пустот (пустых или заполненных жидкостью) , а V – общий объем почвы.
Пористость обычно используется параллельно с коэффициентом пористости почвы (e), который определяется как отношение объема пустот к объему твердых веществsl. Плотность и коэффициент пустотности взаимосвязаны следующим образом:
e = n /(1-n) и n = e / (1+e)
Плотность почвы зависит от консистенции и уплотнения почвы. На это непосредственно влияет уплотнение.
Типичные значения пористости почвы для различных грунтов
Ниже приведены некоторые типичные значения пористости почвы для различных типов почв USCS в нормально уплотненном состоянии, если не указано иное. Эти значения следует использовать только в качестве ориентира при решении геотехнических задач; однако часто необходимо учитывать конкретное состояние каждой инженерной задачи для соответствующего выбора геотехнических параметров.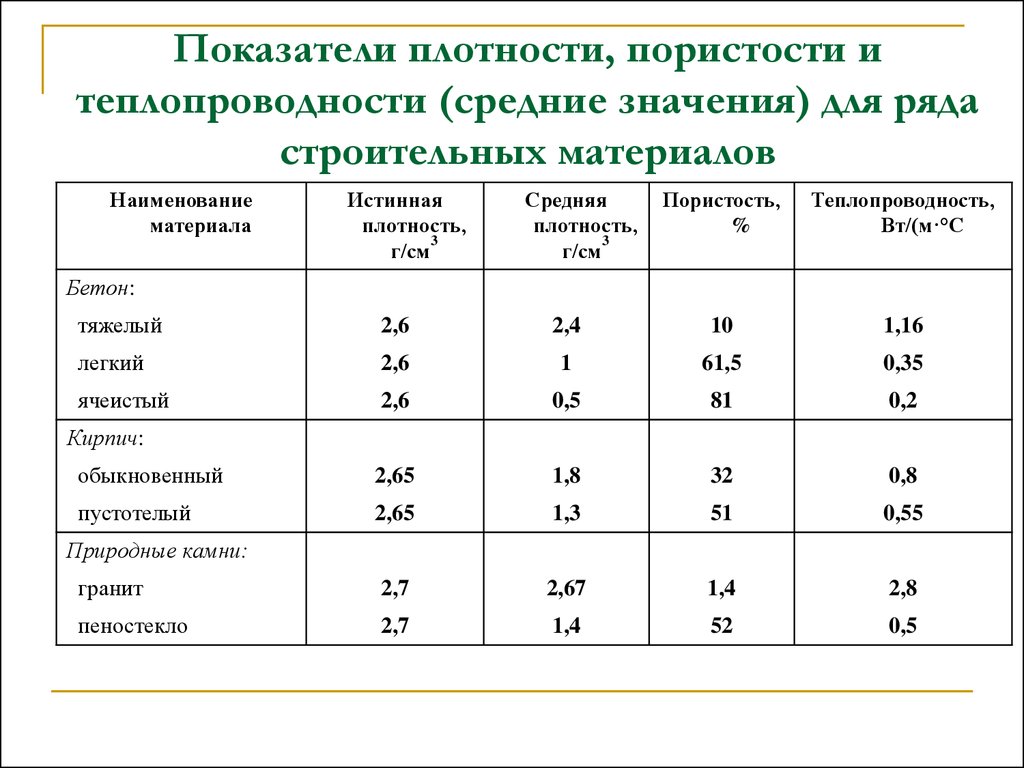
| Описание | USCS | Пористость [-] | Артикул | ||
| мин | макс. | Конкретное значение | |||
| Хорошо отсортированный гравий, песчано-гравийный с небольшим содержанием мелких частиц или без них | ГВт | 0,21 | 0,32 | [1], | |
| Гравий плохого качества, песчано-гравийный с небольшим содержанием мелких частиц или без них | ГП | 0,21 | 0,32 | [1], | |
| Илистый гравий, илистый песчаный гравий | ГМ | 0,15 | 0,22 | [1], | |
| Гравий | (ГВ-ГП) | 0,23 | 0,38 | [2], | |
| Глинистый гравий, глинисто-песчаный гравий | ГК | 0,17 | 0,27 | [1], | |
| Ледниковый тилл, очень смешаннозернистый | (ГК) | — | — | 0,20 | [4 цитируется в 5] |
| Хорошо отсортированные пески, гравийные пески, с небольшим содержанием мелких частиц или без них | SW | 0,22 | 0,42 | [1], [2], | |
| Крупный песок | (ПО) | 0,26 | 0,43 | [2], | |
| Мелкий песок | (ПО) | 0,29 | 0,46 | [2], | |
| Пески плохого качества, гравийные пески с небольшим содержанием мелких частиц или без них | СП | 0,23 | 0,43 | [1], [2], | |
| Илистые пески | См | 0,25 | 0,49 | [1], [2], | |
| Глинистые пески | СК | 0,15 | 0,37 | [1], | |
| Илы неорганические, алевритовые или глинистые мелкозернистые пески со слабой пластичностью | мл | 0,21 | 0,56 | [1], | |
| Однородный неорганический ил | (мл) | 0,29 | 0,52 | [3], | |
| Неорганические глины, алевритовые глины, песчаные глины низкой пластичности | класс | 0,29 | 0,41 | [1], | |
| Органические илы и органоалевритистые глины низкой пластичности | ОЛ | 0,42 | 0,68 | [1], [3], | |
| Илистая или песчаная глина | (CL-OL) | 0,20 | 0,64 | [3], | |
| Неорганические илы высокой пластичности | МХ | 0,53 | 0,68 | [1], | |
| Глины неорганические высокопластичные | Ч | 0,39 | 0,59 | [1], | |
| Мягкая ледниковая глина | — | — | — | 0,55 | [4 цитируется в 5] |
| Жесткая ледниковая глина | — | — | — | 0,38 | [4 цитируется в 5] |
| Глины органические высокопластичные | ОХ | 0,50 | 0,75 | [1], [3], | |
| Мягкая слегка органическая глина | (ОН-ПР) | — | — | 0,66 | [4] цитируется в [5] |
| Торф и другие высокоорганические почвы | Пт | — | — | [4 цитируется в 5] | |
| мягкая очень органическая глина | (Пт) | — | — | 0,75 | [4] цитируется в [5] |
ССЫЛКИ
- Швейцарский стандарт SN 670 010b, Характеристические коэффициенты грунтов, Ассоциация швейцарских инженеров-дорожников
- Дас, Б.
 , Продвинутая механика грунтов. Тейлор и Фрэнсис, Лондон и Нью-Йорк, 2008 г.
, Продвинутая механика грунтов. Тейлор и Фрэнсис, Лондон и Нью-Йорк, 2008 г. - Хаф, Б., Основы инженерии почвы. Компания Рональда Пресса, Нью-Йорк, 1969.
- Терзаги, К., Пек, Р. и Месри, Г., Механика грунтов в инженерной практике. Уайли, Нью
Йорк, 1996. - Obrzud R. & Truty, A. МОДЕЛЬ ЗАКРЕПЛЯЮЩЕГОСЯ ГРУНТА — ПРАКТИЧЕСКОЕ РУКОВОДСТВО Z Отчет Soil.PC 100701, пересмотренный 31.01.2012
.
.
Ссылка:
Geotechdata.info, Коэффициент пустотности почвы, http://geotechdata.info/parameter/soil-void-ratio.html (по состоянию на 16 ноября 2013 г.).
Другие параметры грунта
- » Угол трения
- » Сплоченность
- » Масса сухой упаковки
- » Модуль Юнга
- » Коэффициент пустот
- » Коэффициент проницаемости грунта
- » Пористость почвы
Вы можете редактировать эту страницу? Отправьте нам электронное письмо по адресу editor@geotechdata. info
info
Влияние пористости на кривые водоудерживающей способности почвы: теоретические и экспериментальные аспекты
На этой странице
РезюмеВведениеВыводыДоступность данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме
Изменение пористости является общей характеристикой природных грунтов в задачах взаимодействия жидкости и твердой фазы, что может привести к очевидному изменению кривой водоудержания почвы (КВВП). Влияние пористости на явление удерживания воды в почве исследуется с помощью теоретической модели и экспериментального теста в этом исследовании. Теоретически предложена модель, выражающая изменение всасывания с пористостью и эффективной насыщенностью. Модель основана на идеализации трехфазных пористых материалов, структура пор которых однородна и изотропна. Он учитывает влияние пористости на удержание влаги в почве с использованием четырех параметров с ясным физическим значением. Представленная модель позволяет получить ОКР при любой пористости, что уменьшит количество испытаний, необходимых для характеристики гидравлического поведения грунта.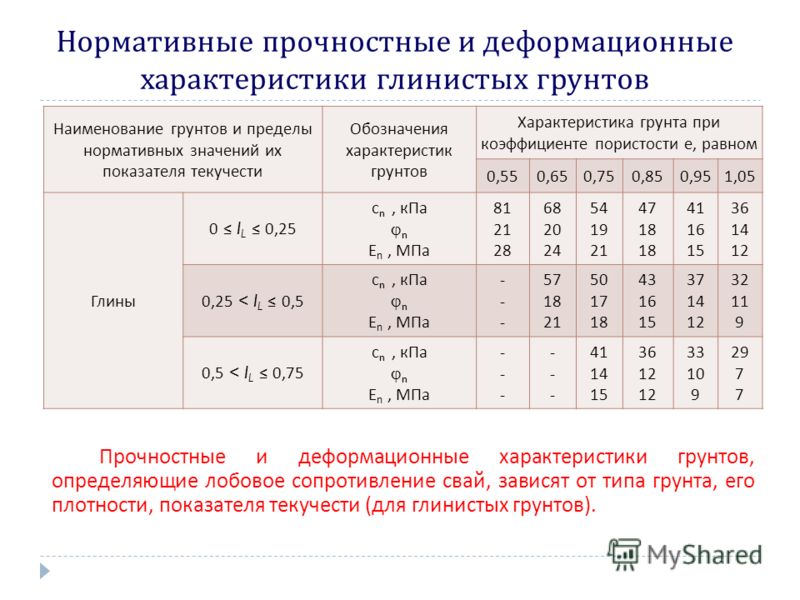 Проведен лабораторный эксперимент на супесях различной пористости. Результаты испытаний показывают, что всасывание существенно меняется с изменением пористости и уменьшается с увеличением пористости. Состав подтвержден как данными испытаний, так и литературными данными для бентонита FEBEX и глины Boom. Очень хорошие совпадения между измеренными и прогнозируемыми результатами показывают, что модель SWRC надежна и применима для различных почв.
Проведен лабораторный эксперимент на супесях различной пористости. Результаты испытаний показывают, что всасывание существенно меняется с изменением пористости и уменьшается с увеличением пористости. Состав подтвержден как данными испытаний, так и литературными данными для бентонита FEBEX и глины Boom. Очень хорошие совпадения между измеренными и прогнозируемыми результатами показывают, что модель SWRC надежна и применима для различных почв.
1. Введение
Кривая водоудерживающей способности почвы (SWRC) определяется как взаимосвязь между матричным всасыванием и степенью насыщения в ненасыщенных почвах. Соотношение SWRC является ключевым гидравлическим свойством для описания явления потока жидкости в ненасыщенных грунтах, на которое может влиять пористость или плотность грунта [1, 2]. Изменение пористости почвы является обычным явлением в задачах взаимодействия жидкости и твердого тела [3, 4], и это изменение приведет к очевидному изменению SWRC [5]. Иногда необходимо предсказать SWRC для почвы с различной пористостью. Однако многие традиционные модели SWRC [6–11] не учитывают влияние пористости на SWRC, что может привести к неточным результатам. Следовательно, необходимо установить взаимосвязь между пористостью и SWRC в сельскохозяйственной инженерии и геотехнической инженерии, особенно в том, что касается оползней, вызванных водой [12–14], и техники сопряжения вода-порода [15–17].
Однако многие традиционные модели SWRC [6–11] не учитывают влияние пористости на SWRC, что может привести к неточным результатам. Следовательно, необходимо установить взаимосвязь между пористостью и SWRC в сельскохозяйственной инженерии и геотехнической инженерии, особенно в том, что касается оползней, вызванных водой [12–14], и техники сопряжения вода-порода [15–17].
Были предложены различные модели SWRC для учета влияния пористости путем связывания всасывания и/или индекса распределения пор по размерам с коэффициентом пустотности или плотностью. Первая группа моделей связала текущую пористость с исходной пористостью с помощью закона изменения объема, который описывает соотношение между всасыванием и пористостью [18–22]. Трудно установить прямую связь между объемом и всасыванием, которое обычно связано с гидравлическими и механическими процессами почвы. В некоторых моделях использовалась эмпирическая функция объема для количественной оценки влияния начальной пористости на SWRC на основе экспериментальных данных [21]. Даже для самых простых моделей [23] для описания изменения объема грунта требуется множество дополнительных параметров. Другие подходы описывают зависимость пористости путем сдвига SWRC с зависящим от пористости значением входа воздуха или индексом распределения пор по размерам [3, 24–28]. Такие подходы могут быть использованы в законах SWRC, которые содержат элемент стоимости входа в атмосферу, таких как модель Брукса и Кори [7]. Но ненасыщенные почвы представляют собой трехфазные смеси твердого вещества, воды и воздуха. Потоки воды и воздуха в структурированных грунтах зависят не только от гранулометрического состава почвы, но также от формы и распределения пор [29].]. Некоторые важные внутренние соотношения для поровых систем могут не выполняться. Необходимо учитывать влияние распределения, формы и размера пор на SWRC из теории смесей.
Даже для самых простых моделей [23] для описания изменения объема грунта требуется множество дополнительных параметров. Другие подходы описывают зависимость пористости путем сдвига SWRC с зависящим от пористости значением входа воздуха или индексом распределения пор по размерам [3, 24–28]. Такие подходы могут быть использованы в законах SWRC, которые содержат элемент стоимости входа в атмосферу, таких как модель Брукса и Кори [7]. Но ненасыщенные почвы представляют собой трехфазные смеси твердого вещества, воды и воздуха. Потоки воды и воздуха в структурированных грунтах зависят не только от гранулометрического состава почвы, но также от формы и распределения пор [29].]. Некоторые важные внутренние соотношения для поровых систем могут не выполняться. Необходимо учитывать влияние распределения, формы и размера пор на SWRC из теории смесей.
В этой статье представлена модель SWRC, учитывающая влияние пористости, предполагающая, что ненасыщенный грунт представляет собой непрерывную, изотропную и однородную трехфазную смесь пор. Это уравнение выражается законом эффективного насыщения, всасывания и пористости только с четырьмя параметрами. Также проводятся экспериментальные испытания суглинистого песка для изучения влияния пористости на удержание воды. Предложенная модель подтверждена данными испытаний суглинков различной пористости, а также литературными данными для бентонита FEBEX и глины Boom.
Это уравнение выражается законом эффективного насыщения, всасывания и пористости только с четырьмя параметрами. Также проводятся экспериментальные испытания суглинистого песка для изучения влияния пористости на удержание воды. Предложенная модель подтверждена данными испытаний суглинков различной пористости, а также литературными данными для бентонита FEBEX и глины Boom.
2. Вывод модели SWRC, зависящей от пористости
Всасывание, , может быть выражено как отношение между поровым давлением газа () и поровым давлением воды ():
в почве может быть задано как атмосферное давление, так как поток газа относительно свободный потоку воды ([30, 31]). Поэтому остается только определить.
2.1. Давление воды в порах
Хотя структура пор почвы состоит из пор неоднородного размера, а распределение пор довольно сложное, можно предположить, что большинство почв представляют собой непрерывную, изотропную и однородную пористую среду, в которой распределение поровой воды и воздуха также изотропны и однородны в макроскопическом масштабе [29].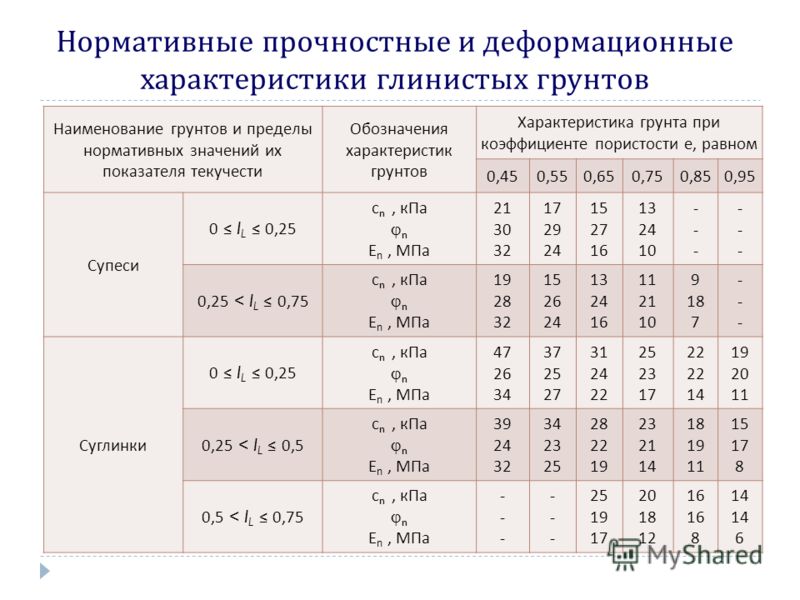 ]. Следовательно, на единицу площади двухмерного (2D) поперечного сечения, прорезающего почву под любым углом, общая площадь пор, площадь порового газа и площадь поровой воды постоянны. Макроскопическая пористость и насыщенность могут быть описаны выражением
]. Следовательно, на единицу площади двухмерного (2D) поперечного сечения, прорезающего почву под любым углом, общая площадь пор, площадь порового газа и площадь поровой воды постоянны. Макроскопическая пористость и насыщенность могут быть описаны выражением
где , и – суммарный объем пор, воды и почвы соответственно.
Вода в порах в основном включает границы раздела вода-твердое тело и вода-газ, а также воду между двумя границами раздела, как показано на рис. 1(а). Для расчета на любом поперечном сечении форма пор может быть произвольной. Здесь поры идеализированы как эллипсы, поскольку их форма может быть круглой или плоской. Эллиптическая пора случайным образом распределяется по произвольному поперечному сечению. Каждая пора содержит идентичный воздушный пузырь эллиптической формы (рис. 1(б)) [29].]. Полная нормальная сила данного поперечного сечения выражается как
где представляет собой поверхностное натяжение воды, представляет собой угол между касательной плоскостью и плоскостью сечения в точке границы раздела вода-газ (рис. 1(b)), и представляет дифференциальную длину . площадь, занятая водой, но не включая границу раздела вода-газ. Дифференциальная площадь представляет собой статическое давление воды в области .
1(b)), и представляет дифференциальную длину . площадь, занятая водой, но не включая границу раздела вода-газ. Дифференциальная площадь представляет собой статическое давление воды в области .
Согласно предположению об изотропии и однородности среды угол в любой точке на границе вода-воздух всегда равен . Часть в уравнении (3) можно выразить как
Другая часть, , в уравнении. (3) переписывается как
Согласно теории науки о поверхности, поверхностное натяжение жидкости можно рассматривать как константу при постоянной температуре [32]. можно описать как
куда ; единицей измерения является Н/м.
Формы эллиптических пузырьков газа и пор представлены двумя полуосями, причем для пор () и и для пузырьков газа (). Пора содержит газовый пузырь, поэтому существуют и . Определяя и , где и , макроскопическая пористость и насыщенность могут быть выражены как
Эквивалентное количество пор на площадь поперечного сечения представлено как , что выражается как . Согласно уравнениям (7) и (8), можно получить и .
Согласно уравнениям (7) и (8), можно получить и .
Периметр эллиптического воздушного пузыря можно записать как . Суммарная длина периметра пузырьков воздуха на поперечном сечении:
Экв. (6) можно переписать как
2.2. Составы новой модели SWRC
Замена уравнения. (10) в уравнение. (1) дает
Уравнение всасывания состоит из функций плотности пор, насыщения, формы пузырьков воздуха и водного стресса. Влияние пористости на всасывание отражается через параметры (пористость), (плотность пор) и (коэффициент формы пузырька воздуха). (плотность пор) связана с пористой структурой почвы и может быть записана как функция пористости. Для выражения отношения используется простая функция. связано с насыщением, и его эффект может быть выражен насыщением. Итак, уравнение (11) можно переписать как
где , в единицах Н/м 2 , остальные параметры безразмерны. и параметры изменены с помощью .
Определение доходности
можно получить из условий что и :
Следовательно,
Уравнение не новое и использовалось многими людьми (включая Брукса, Кори и ван Генухтена). описывает отношение текущего насыщения к максимальному. Отметив, что представляет насыщенность, когда и представляет насыщенность, когда .
описывает отношение текущего насыщения к максимальному. Отметив, что представляет насыщенность, когда и представляет насыщенность, когда .
Функция представляет эффект формы пузырьков воздуха. Его можно приблизительно выразить простой степенной функцией с помощью хорошего метода аппроксимации кривой (рис. 2):
Форма пузырька воздуха, обозначенная значком , должна изменяться в зависимости от , , (температуры) и некоторых других факторов. Из-за сложности измерения непосредственно на практике или разработки аналитической формы функции здесь для простоты используется функция для , где и — параметры, относящиеся к рассматриваемой почве. уравнение (13) можно упростить как
Предлагаемая модель включает четыре параметра, . связано с поверхностным натяжением. Единицей измерения является Н/м 2 , а остальные параметры безразмерны. связано с плотностью пор и связано с пористостью. представляет собой комбинированное влияние температуры, эффектов гистерезиса и других факторов и связано только с пористостью.
3. Валидация
3.1. Подготовка проб и процедура испытаний
Для проверки уравнения. (17) для определения SWRC при различной пористости используется система нажимных пластин. Установка экспериментальной системы показана на рис. 3. Цилиндрический образец грунта (диаметром 70 мм и высотой 20 мм), плотно заключенный в режущее кольцо, помещается на керамический диск, а керамический диск (со значением входа воздуха 500 кПа) хорошо соединяется с днищем. При приложении давления воздуха вода вытекает из образца почвы в камеру, и масса воды измеряется весами.
Тип суглинистого песка (83,92 % песка, 14,19 % ила и 1,89 % глины), добытый в районе Трех ущелий, Китай, использовался в качестве тестового материала. В соответствии со спецификацией испытания почвы были подготовлены три образца, которые были обозначены как L1, L2 и L3 (рис. 4), а соответствующие значения пористости составили 0,4666, 0,4346 и 0,4097 соответственно. Тест начинали с насыщенной почвы и проводили при комнатной температуре (20°C). Степень насыщения, соответствующую каждой ступени отсасывания, рассчитывали из взвешивания истечения воды, образца почвы над тестом и сухого образца после сушки в печи.
Степень насыщения, соответствующую каждой ступени отсасывания, рассчитывали из взвешивания истечения воды, образца почвы над тестом и сухого образца после сушки в печи.
3.2. Проверка по сравнению с экспериментальными результатами
Данные испытаний для суглинистого песка со всеми значениями пористости были приняты для проверки уравнения. (17). В предложенной модели SWRC имеется четыре параметра. Параметры калибруются с использованием нелинейного метода наименьших квадратов (NLS): , , и , соответственно.
На рис. 5 показано сравнение рассчитанного моделью всасывания и данных испытаний для суглинистого песка. Прогнозируемые всасывания хорошо согласуются с данными испытаний, большинство расхождений менее 10%. Измеренные и предсказанные SWRC с использованием предложенной модели при различной пористости показаны на рисунке 6. Можно видеть, что предсказанные SWRC по предложенной модели хорошо совпадают с экспериментальными данными, что указывает на то, что уравнение. (17) успешно воспроизводит влияние пористости на SWRC. На рис. 6 также видно, что как расчетные, так и измеренные значения отсасывания уменьшаются с увеличением пористости, а форма и положение ОКР явно изменяются при различной пористости.
(17) успешно воспроизводит влияние пористости на SWRC. На рис. 6 также видно, что как расчетные, так и измеренные значения отсасывания уменьшаются с увеличением пористости, а форма и положение ОКР явно изменяются при различной пористости.
3.3. Проверка по литературным данным
Для дальнейшего изучения применимости предложенной модели используются экспериментальные данные для двух разных почв, найденные в литературе.
Первый – это бентонит FEBEX (глина: 92 %; ил и песок: 8 %), представляющий собой разновидность инженерной глины [29]. Здесь были выбраны три сухие плотности; они равны г/см 3 , г/см 3 и г/см 3 соответственно. Температура испытания составляла 20°С. Пористость рассчитывали как , где г/см 3 . Таким образом, соответствующие значения пористости трех образцов равны , и , соответственно.
Второй – глина Бум [33]. Этот материал был получен путем уплотнения натуральной глины Boom. Глина Бум (10–20 % смектита, 20–30 % иллита и 20–30 % каолинита) имеет предел пластичности 29 %, предел текучести 56 % и удельный вес 2,7, а половина частиц меньше 2 μ м. Испытываемые образцы были приготовлены при плотности в сухом состоянии 1,37 г/см 3 и 1,67 г/см9.0490 3 , а соответствующие коэффициенты пустот равны 0,932 и 0,591 соответственно. Так, пористость двух образцов составляет 0,4824 и 0,3715 соответственно. Температуру испытания поддерживали на уровне 22°С.
Испытываемые образцы были приготовлены при плотности в сухом состоянии 1,37 г/см 3 и 1,67 г/см9.0490 3 , а соответствующие коэффициенты пустот равны 0,932 и 0,591 соответственно. Так, пористость двух образцов составляет 0,4824 и 0,3715 соответственно. Температуру испытания поддерживали на уровне 22°С.
Четыре параметра в уравнении (17) рассчитаны с использованием метода NLS и перечислены в таблице 1. На рисунке 7 экспериментальные данные для двух разных почв соответствуют уравнению. (17). Он показывает очень хорошие совпадения между предсказаниями модели и экспериментальными данными с незначительными расхождениями.
4. Выводы
Разработана теоретическая модель для описания влияния пористости на SWRC. Модель получена для трехфазной смеси с идеализированной структурой пор. Идеализированная форма пузырьков воздуха и система пор отвечают эквивалентности макроскопических физических эффектов. На этой основе предлагается модель SWRC, в которой всасывание выражается как функция пористости и эффективной насыщенности. В модели имеется четыре характеристических параметра , имеющих четкий физический смысл. связано с поверхностным натяжением; связано с пористостью; представляет комбинированное влияние температуры, эффектов гистерезиса и других факторов; и относится только к пористости. Экспериментальная проверка этой модели была проведена на ВОРК из суглинков. Предсказания модели близки к результатам испытаний, которые также показывают, что всасывание уменьшается с увеличением пористости, а форма и положение ОТК явно изменяются при различной пористости. Прогнозы предложенной модели также сравнивались с экспериментальными результатами для бентонита FEBEX и глины Boom в опубликованных статьях. Хорошие совпадения показывают, что модель SWRC надежна и применима для широких почв.
В модели имеется четыре характеристических параметра , имеющих четкий физический смысл. связано с поверхностным натяжением; связано с пористостью; представляет комбинированное влияние температуры, эффектов гистерезиса и других факторов; и относится только к пористости. Экспериментальная проверка этой модели была проведена на ВОРК из суглинков. Предсказания модели близки к результатам испытаний, которые также показывают, что всасывание уменьшается с увеличением пористости, а форма и положение ОТК явно изменяются при различной пористости. Прогнозы предложенной модели также сравнивались с экспериментальными результатами для бентонита FEBEX и глины Boom в опубликованных статьях. Хорошие совпадения показывают, что модель SWRC надежна и применима для широких почв.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, включены в статью.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Это исследование было поддержано Национальной ключевой программой исследований и разработок Китая (номер гранта 2017YFC1501100), Национальным фондом естественных наук Китая (номера грантов 51939004 и 51279090) и Открытым фондом Ключевой лаборатории геологических опасностей. в районе водохранилища «Три ущелья», Министерство образования, Китайский университет «Три ущелья» (номер гранта 2020KDZ11).
в районе водохранилища «Три ущелья», Министерство образования, Китайский университет «Три ущелья» (номер гранта 2020KDZ11).
Ссылки
C. A. Burger и C. D. Shackelford, «Характеристические кривые грунт-вода и двойная пористость смесей песка и диатомита», Journal of Geotechnical and Geoenvironmental Engineering , vol. 127, нет. 9, стр. 790–800, 2001.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Ю. Фаттах, Н. М. Салим, Э. Дж. Иршайид, «Определение характеристической кривой почва-вода ненасыщенных бентонит-песчаных смесей», Экологические науки о Земле , vol. 76, нет. 5, с. 201, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Ассулин, «Моделирование взаимосвязи между объемной плотностью почвы и кривой удержания воды», Журнал Vadose Zone , том.
 5, нет. 2, стр. 554–563, 2006 г.
5, нет. 2, стр. 554–563, 2006 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
X. Zhang, Y. Wu, E. Zhai и P. Ye, «Анализ сопряжения динамики тепла и воды и глубины промерзания в зоне сезонного замерзания», Журнал гидрологии , с. 125603, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Чжоу, Ю. Фан, В. Ченг и Дж. Чжан, «Фрактальная модель для интерпретации гидравлических свойств, зависящих от пористости, для ненасыщенных грунтов», Advance in Civil Engineering , vol. 2019, статья 3965803, стр. 1–13, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Обертен, М. Мбонимпа, Б. Бюссьер и Р. П. Шапюи, «Модель для прогнозирования кривой водоудержания на основе основных геотехнических свойств», Канадский геотехнический журнал , том.
 40, нет. 6, стр. 1104–1122, 2003.
40, нет. 6, стр. 1104–1122, 2003.Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Х. Брукс и А. Т. Кори, 1964, Гидравлические свойства пористой среды. Бумага по гидрологии №. 3, Университет штата Колорадо, Форт-Коллинз, Колорадо.
Д. Г. Фредлунд и А. Син, «Уравнения для характеристической кривой почва-вода», Канадский геотехнический журнал , том. 31, нет. 4, стр. 521–532, 199.4.
Посмотреть по адресу:
Сайт издателя | Google Scholar
XS Li, «Моделирование гистерезисной реакции для произвольных путей смачивания/высыхания», Computers and Geotechnics , vol. 32, нет. 2, стр. 133–137, 2005 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Муалем, «Новая модель для прогнозирования гидравлической проводимости ненасыщенных пористых сред», Water Resources Research , vol.
 12, стр. 564–566, 1976.
12, стр. 564–566, 1976.Просмотр по адресу:
Google Scholar
М. Т. ван Генухтен, «Уравнение в закрытой форме для прогнозирования гидравлической проводимости ненасыщенных почв», Журнал Американского общества почвоведов , том. 44, нет. 5, стр. 892–898, 1980.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Q. Meng, H. Wang, M. Cai, W. Xu, X. Zhuang, and T. Rabczuk, «Трехмерное мезомасштабное вычислительное моделирование почвенно-каменных смесей с вогнутыми частицами», Инженерная геология , вып. 277, статья 105802, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Q. Meng, H. Wang, M. He, J. Gu и L. Yang, «Прогнозирование смещения вызванных водой оползней с использованием рекуррентной модели глубокого обучения», European Journal of Environmental and Civil Машиностроение , вып.
 2020, стр. 1–15, 2020.
2020, стр. 1–15, 2020.Посмотреть по адресу:
Сайт издателя | Google Scholar
Л. Ян, В. Сюй, Х. Ван и др., «Контроль дренажа на оползне Дунлинсин (Китай), вызванном дождями и колебаниями уровня воды в водохранилище», Оползни , том. 16, нет. 8, стр. 1583–1593, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C. Zhu, Z. Yan, Y. Lin, F. Xiong и Z. Tao, «Проектирование и применение системы мониторинга для проекта глубокого железнодорожного котлована», IEEE Access , vol. . 7, стр. 107591–107601, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C. Zhu, X. Xu и W. Liu, «Анализ повреждений гипсовой породы при размягчении с учетом времени погружения в воду на основе лабораторного эксперимента», Доступ IEEE , том.
 7, стр. 125575–125585, 2019.
7, стр. 125575–125585, 2019.Посмотреть по адресу:
Сайт издателя | Google Scholar
C. Zhu, M. He, M. Karakus, X. Cui и Z. Tao, «Исследование механизма опрокидывания слоистого склона, препятствующего наклону, из-за раскопок с помощью физического моделирования», Rock Mechanics and Горная техника , т. 1, с. 53, нет. 11, стр. 5029–5050, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Машин, «Прогнозирование зависимости степени насыщения от пористости и всасывания с использованием принципа эффективного напряжения для ненасыщенных грунтов», Международный журнал численных и аналитических методов в геомеханике , том. 34, нет. 1, стр. 73–90, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д.
 Шэн и А. Чжоу, «Соединение гидравлических моделей с механическими для ненасыщенных грунтов», Канадский геотехнический журнал , том. 48, нет. 5, стр. 826–840, 2011.
Шэн и А. Чжоу, «Соединение гидравлических моделей с механическими для ненасыщенных грунтов», Канадский геотехнический журнал , том. 48, нет. 5, стр. 826–840, 2011.Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. А. Сун, Д. К. Шэн, Х. Б. Цуй и С. В. Слоан, «Упругопластическая гидромеханическая модель, зависящая от плотности, для ненасыщенных уплотненных грунтов», Международный журнал численных и аналитических методов в геомеханике , том. 31, нет. 11, стр. 1257–1279, 2007.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тарантино, «Модель удержания воды для деформируемых грунтов», Geotechnique , vol. 59, нет. 9, стр. 751–762, 2009.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С.
 Дж. Уилер, Р. С. Шарма и М. С. Р. Буиссон, «Соединение гидравлического гистерезиса и поведения напряжения и деформации в ненасыщенных грунтах», Геотехника , том. 53, нет. 1, стр. 41–54, 2003 г.
Дж. Уилер, Р. С. Шарма и М. С. Р. Буиссон, «Соединение гидравлического гистерезиса и поведения напряжения и деформации в ненасыщенных грунтах», Геотехника , том. 53, нет. 1, стр. 41–54, 2003 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. К. Флориан и Р. Хорн, «Моделирование кривой водоудержания почвы для условий переменной пористости», , журнал Vadose Zone, , том. 4, стр. 602–613, 2005 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Галлиполи, «Гистерезисная модель удержания воды почвой, учитывающая циклические изменения коэффициента всасывания и пористости», Геотехника , том. 62, нет. 7, стр. 605–616, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д.
 Галлиполи, С. Дж. Уилер и М. Карстунен, «Моделирование изменения степени насыщения деформируемого ненасыщенного грунта», Géotechnique , vol. 53, нет. 1, стр. 105–112, 2003 г.
Галлиполи, С. Дж. Уилер и М. Карстунен, «Моделирование изменения степени насыщения деформируемого ненасыщенного грунта», Géotechnique , vol. 53, нет. 1, стр. 105–112, 2003 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Хуанг, С. Л. Барбур и Д. Г. Фредлунд, «Разработка и проверка функции коэффициента проницаемости для деформируемого ненасыщенного грунта», Канадский геотехнический журнал , том. 35, нет. 3, стр. 411–425, 1998.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Нут и Л. Лалуи, «Достижения в моделировании гистерезисной кривой водоудержания в деформируемых грунтах», Computers and Geotechnics , vol. 35, нет. 6, стр. 835–844, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А.
 Чжоу, Д. Шэн и Дж. П. Картер, «Моделирование влияния начальной плотности на характеристические кривые почва-вода», Геотехника , том. 62, нет. 8, стр. 669–680, 2012.
Чжоу, Д. Шэн и Дж. П. Картер, «Моделирование влияния начальной плотности на характеристические кривые почва-вода», Геотехника , том. 62, нет. 8, стр. 669–680, 2012.Посмотреть по адресу:
Сайт издателя | Google Scholar
Ф. Тонг, Л. Цзин и Т. Бин, «Модель кривой водоудержания для моделирования связанных термогидромеханических процессов в геологических пористых средах», Transport in Porous Media , vol. . 91, нет. 2, стр. 509–530, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Л. А. Ричардс, «Капиллярная проводимость жидкостей через пористые среды», Журнал прикладной физики , том. 1, нет. 5, стр. 318–333, 1931.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C.
 Liu, F. Tong, L. Biao, and Z. Yitong, «Модель кривой водоудержания, описывающая влияние температуры», European Journal of Soil Science , vol. 71, стр. 44–54, 2020.
Liu, F. Tong, L. Biao, and Z. Yitong, «Модель кривой водоудержания, описывающая влияние температуры», European Journal of Soil Science , vol. 71, стр. 44–54, 2020.Посмотреть по адресу:
Сайт издателя | Google Scholar
X. Zhang, C. Zhao, Y. Liu, and G. Cai, «Моделирование исследования взаимосвязи между деформацией и кривой водоудержания», Китайский журнал гражданского строительства , том. 44, pp. 119–126, 2011.
Посмотреть по адресу:
Google Scholar
E. Romero, A. Gens и A. Lloret, «Влияние всасывания на уплотненную глину в неизотермических условиях», Геотехника , том. 53, нет. 1, стр. 65–81, 2003 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Copyright
Copyright © 2020 Chang Liu et al.

 5-8,0
5-8,0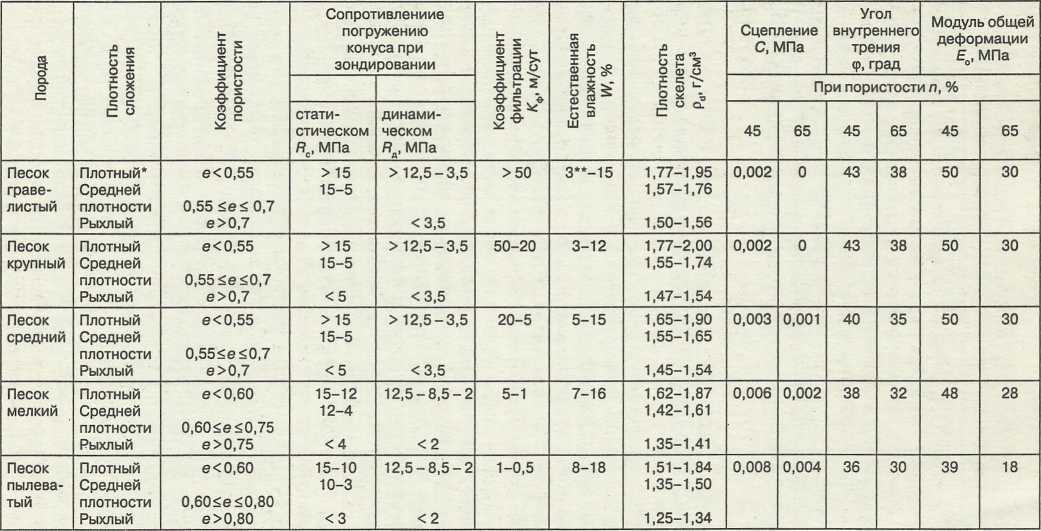 4-12,4
4-12,4

 , Продвинутая механика грунтов. Тейлор и Фрэнсис, Лондон и Нью-Йорк, 2008 г.
, Продвинутая механика грунтов. Тейлор и Фрэнсис, Лондон и Нью-Йорк, 2008 г. 5, нет. 2, стр. 554–563, 2006 г.
5, нет. 2, стр. 554–563, 2006 г. 40, нет. 6, стр. 1104–1122, 2003.
40, нет. 6, стр. 1104–1122, 2003. 12, стр. 564–566, 1976.
12, стр. 564–566, 1976. 2020, стр. 1–15, 2020.
2020, стр. 1–15, 2020.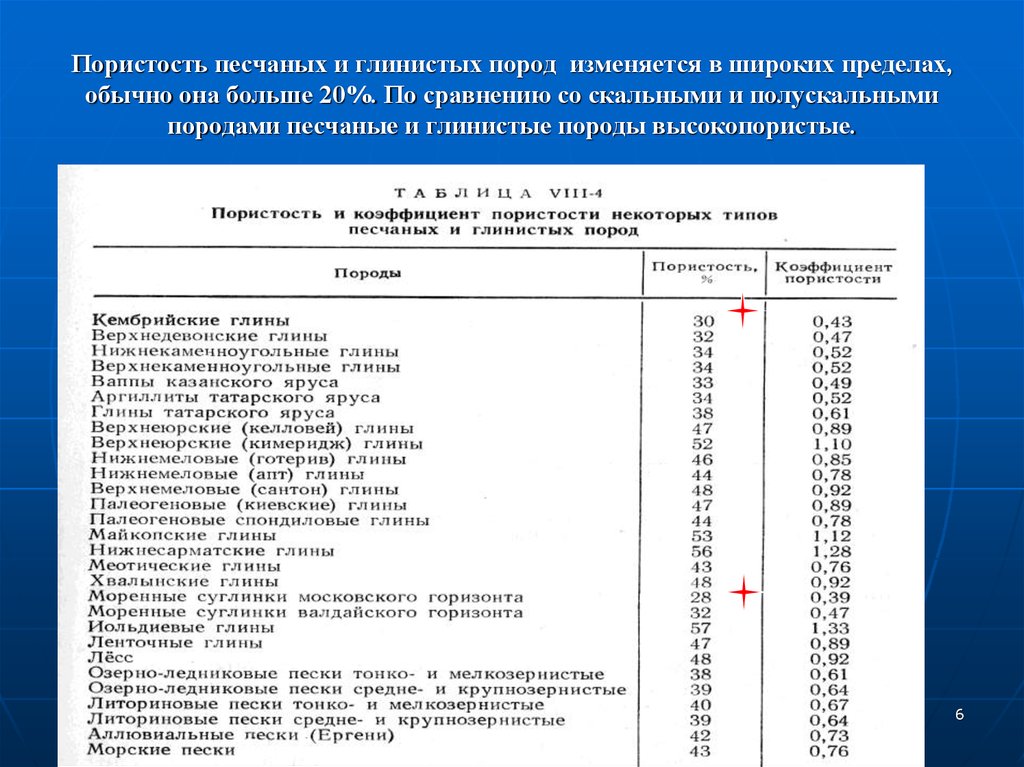 7, стр. 125575–125585, 2019.
7, стр. 125575–125585, 2019. Шэн и А. Чжоу, «Соединение гидравлических моделей с механическими для ненасыщенных грунтов», Канадский геотехнический журнал , том. 48, нет. 5, стр. 826–840, 2011.
Шэн и А. Чжоу, «Соединение гидравлических моделей с механическими для ненасыщенных грунтов», Канадский геотехнический журнал , том. 48, нет. 5, стр. 826–840, 2011. Дж. Уилер, Р. С. Шарма и М. С. Р. Буиссон, «Соединение гидравлического гистерезиса и поведения напряжения и деформации в ненасыщенных грунтах», Геотехника , том. 53, нет. 1, стр. 41–54, 2003 г.
Дж. Уилер, Р. С. Шарма и М. С. Р. Буиссон, «Соединение гидравлического гистерезиса и поведения напряжения и деформации в ненасыщенных грунтах», Геотехника , том. 53, нет. 1, стр. 41–54, 2003 г. Галлиполи, С. Дж. Уилер и М. Карстунен, «Моделирование изменения степени насыщения деформируемого ненасыщенного грунта», Géotechnique , vol. 53, нет. 1, стр. 105–112, 2003 г.
Галлиполи, С. Дж. Уилер и М. Карстунен, «Моделирование изменения степени насыщения деформируемого ненасыщенного грунта», Géotechnique , vol. 53, нет. 1, стр. 105–112, 2003 г. Чжоу, Д. Шэн и Дж. П. Картер, «Моделирование влияния начальной плотности на характеристические кривые почва-вода», Геотехника , том. 62, нет. 8, стр. 669–680, 2012.
Чжоу, Д. Шэн и Дж. П. Картер, «Моделирование влияния начальной плотности на характеристические кривые почва-вода», Геотехника , том. 62, нет. 8, стр. 669–680, 2012. Liu, F. Tong, L. Biao, and Z. Yitong, «Модель кривой водоудержания, описывающая влияние температуры», European Journal of Soil Science , vol. 71, стр. 44–54, 2020.
Liu, F. Tong, L. Biao, and Z. Yitong, «Модель кривой водоудержания, описывающая влияние температуры», European Journal of Soil Science , vol. 71, стр. 44–54, 2020.