Содержание
Стропильные фермы железобетонные: классификация и особенности использования
- Производство элементов несущих конструкций из бетона
- Конструкция железобетонных стропильных ферм
- Типы: безраскосые, раскосые, типовые
- Особенности монтажа
Многообразие конструкций перекрытий на современном рынке значительно упростило процесс возведения зданий, сократив тем самым сроки строительства крыш. Относительно недавно их собирали прямо на стройплощадке из сборных элементов, а сегодня для покрытия сооружений используют готовые стропильные фермы.
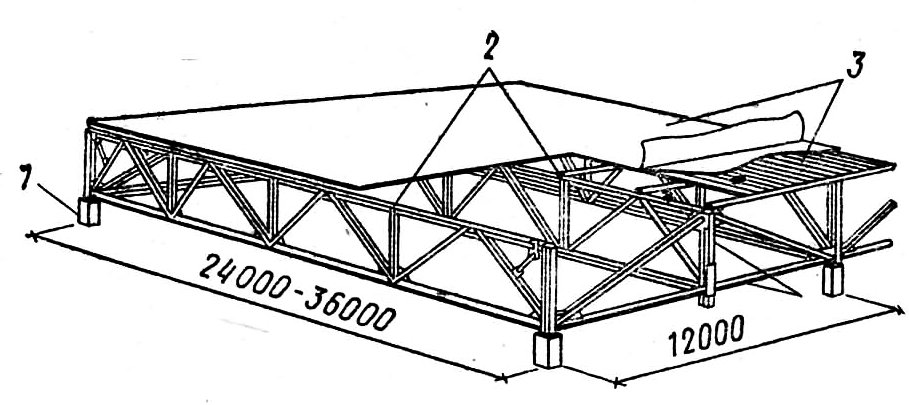
Стропильные фермы железобетонные в зависимости от назначения строения, материала покрытия, способа их опирания и других факторов могут иметь различные типы и очертания. Возможности их применения достаточно широкие:
- здания могут иметь пролеты до 24 м и более:
- кровля – быть как малоуклонной, так и скатной,
- покрытие зданий может быть как с фонарями, так и без и т.
д. Подобные конструкции нашли особое применение в зданиях промышленного типа и складских.
Отличаются:
- высокой прочностью,
- жесткостью,
- трещино- и морозостойкостью, что позволяет эксплуатировать их в агрессивной газообразной среде,
- хорошими противопожарными свойствами.
Производство элементов несущих конструкций из бетона ↑
Железобетонные фермы производят из конструкционного бетона, тяжелого или легкого, в основном это керамзитобетон и аглопоритобетон. Их изготавливают в одно- или многоярусных стендах-камерах. На каждом из них обычно устанавливают несколько металлических форм с паровой рубашкой. Раскосы и стойки, соответственно, на вибростоле в специальных в кассетных формах, закладывают их в процессе армирования.
Для нижних поясов при армировании используют струнопакеты из высокопрочной проволоки (ø 5 мм), а для верхних – обычные стержни. Высокопрочную проволоку натягивают гидродомкратами и добавляют бетоноукладчиками бетон.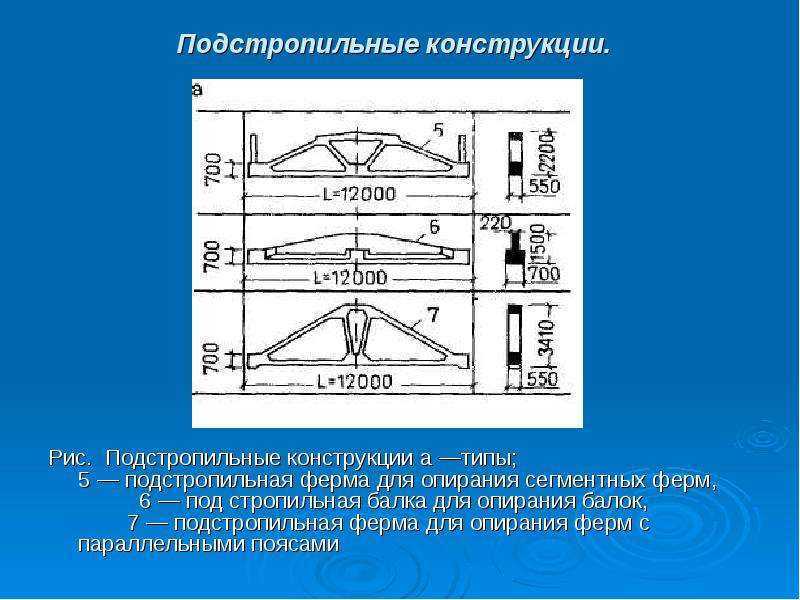
Через 2–3 часа изделие проходит термическую обработку. Качество предварительно напряженных изделий регулярно проверяется путем нагружения, предусмотренного в проектных чертежах.
Маркировка
Их маркируют, используя буквенно-цифровые обозначения, разделенные дефисами. Для обозначения типа и размера используют буквы, а цифрами – всю остальную информацию, типа длины в метрах, ее несущей способности, класса напрягаемой арматуры, марки бетона и другую. Буквами также обозначается проницаемость бетона, то есть возможность использования конструкции в агрессивных условиях:
- Н –нормальная,
- П – пониженная,
- С – сейсмоустойчивость до 8 баллов.
Конструкция железобетонных стропильных ферм ↑
Ферма создает практически своеобразный каркас, определяющий дальнейшие очертания крыши и другие особенности перекрытий. Структура этих бетонных конструкций, придающих каркасу прочность, жесткость и устойчивость, имеет довольно сложную схему, содержащую значительное количество армированных элементов и стали.
Это очевидный факт, поскольку функции несущих платформ, которые они выполняют, требуют такой прочности и надежности, чтобы была обеспечена устойчивость здания в экстремальных условиях.
Использование при их производстве специальных легких марок бетона позволяет существенно снизить вес конструкции без потери качества. Арматурная сталь высокопрочной марки, традиционно входящая во внутреннюю структуру, имеет исключительные антикоррозийные свойства. Поэтому кровля оказывается неуязвимой к воздействию влаги или мороза.
Контур образуют два его пояса, которые работают на изгиб, а решетку – раскосы и стойки, работающие на осевые усилия. Различают следующие их виды:
- сегментные – отличаются верхним поясом очертания и раскосной решеткой;
- полигональные –пояса в них либо параллельные, имеют трапециевидное очертание, то есть отличаются раскосной решеткой и малым углом уклона верхнего пояса;
Сегментные фермы иногда заменяют на полигональные, в которых элементы верхнего пояса в пределах базовых узлов спрямлены.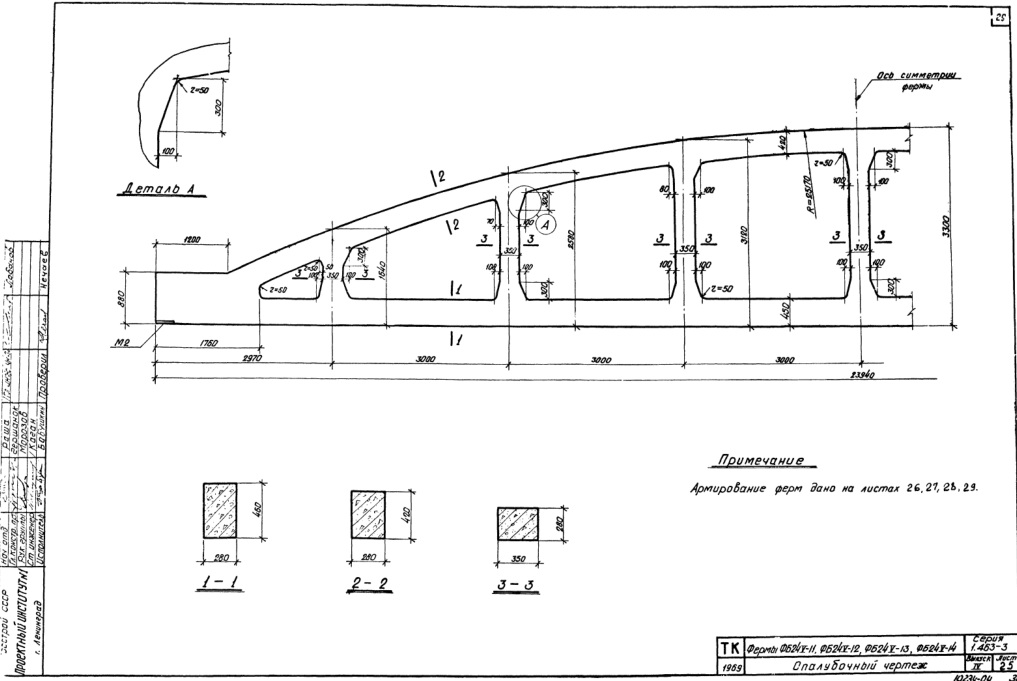
Это значительно экономичнее использования треугольных или прямоугольных очертаний.
- арочные безраскосные – имеют жесткие узлы;
- раскосные арочные – характеризуются криволинейными очертаниями верхнего пояса и редкой решеткой.
Типы: безраскосые, раскосые, типовые ↑
- Для строений с малоуклонной кровлей используют безраскосые фермы, снабженные в верхнем поясе дополнительными стойками. Как правило, это здания с большими системами коммуникаций, размещенных в пределах фермы. Их устанавливают с шагом в 6 (при подвесном транспорте) или 12 м.
- Безраскосными треугольными конструкциями перекрывают однопролетные неотапливаемые здания с пролетом в 6, 9, 12 и 18 м, под асбестоцементные волнистые листы.
- Сегментные раскосые и безраскосые применяют для скатных кровель.
- Типовые ЖБИ используют для перекрытия одноэтажных одно- и многопролетных зданий (пролеты – 18 и 24 м ) под рулонные материалы.
Типовых вариантов довольно много, и для них используются следующие обозначения:
- ФС – раскосные фермы для скатных крыш,
- ФБС – безраскосные для скатных крыш,
- ФП – под покрытия из плит, равных по длине пролету,
- ФПМ – для малоуклонной кровли без преднапряжения,
- ФПН – для малоуклонных крыш с преднапряженными стойками,
- ФБМ – безраскосные для малоуклонной скатной крыши,
- ФПС – для скатной,
- ФТ – безраскосные треугольного очертания для скатной.
Особенности монтажа ↑
Использование конструкций этого типа требует тщательного расчета несущей способности строения. Стропильные конструкции из железобетона крепят к закладным деталям, которые расположены в колоннах или несущих стенах. Еще до начала монтажа проводят проверку качества элементов, их размеров, расположения закладных деталей, подготавливают места опирания. Для приваривания закладных деталей фермы к опорам в составе монтажной бригады должен обязательно участвовать сварщик.
Продольную жесткость конструкции обеспечивают при помощи металлических прогонов, которые приваривают к закладным деталям. В зависимости от типа кровельного покрытия его укладывают либо нf обрешетку, либо непосредственно к прогонам.
© 2022 stylekrov.ru
Железобетонные фермы: разновидности, для чего используют
Для проектирования перекрытий больших пролетов кровли в строительстве жилых одноэтажных и зданий промышленного назначения изготавливают железобетонные фермы.
Устанавливают их с целью безопасности и удобной эксплуатации. С помощью установки такой конструкции осуществляется перераспределение получаемого веса на стены здания.
Фермы представляют собой каркас из соединенной арматуры. Верх и низ опоясывают стяжки. Стойки — вертикальные элементы конструкции, а расколы — части под наклоном. Между ними находятся раскосы и стойки, составные части решетки, а места их соединения называют узлами.
Содержание
- Разновидности ферм
- Размеры железобетонных конструкций
- Расшифровка маркировки изделий
- Для чего используют?
- Как изготовить конструктивный элемент?
Разновидности ферм
Стропильные ЖБ фермы имеют различные типы и очертания. Внешний вид зависит от покрытия, расположения. Нижний пояс фермы имеет растянутую форму, а раскосы по краям армируют прочной и предварительно растянутой арматурой для снижения расхода металла. В элементах железобетонной конструкции, где арматура без высокой прочности, детали выполняют без предварительного напряжения.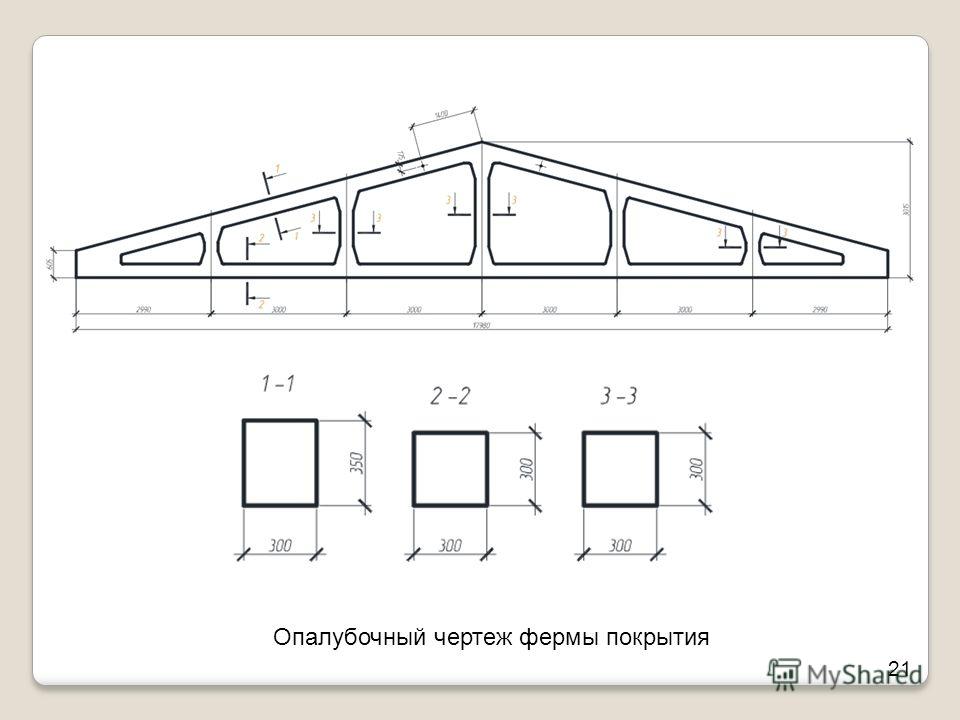
Бывают сегментчатые, арочные, треугольные и с дополнительными параллельными поясами. Все изделия объединены в 2 основные группы: стропильные и безстропильные.
Существует несколько видов данных изделий, применяемых для различных конфигураций крыш.
Стропильные железобетонные конструкции используют для сооружения:
- покрытий с основой из плит и длиной, которая соответствует пролету;
- построек крыш с наклоном;
- зданий с малым уклоном без предварительного напряжения и с его применением.
Безстропильные железобетонные изделия включают в себя:
- раскосные фермы для построек с уклоном;
- безраскосные фермы с наклоном и незначительным уклоном, а также треугольные.
Размеры железобетонных конструкций
Согласно нормативной документации такие изделия изготавливаются с определенными размерами.
Все фермы изготавливаются согласно стандарту из тяжелого бетона, в некоторых элементах используется легкий. Широко применяемые сооружения с пролетами 18, 24, 36 метров.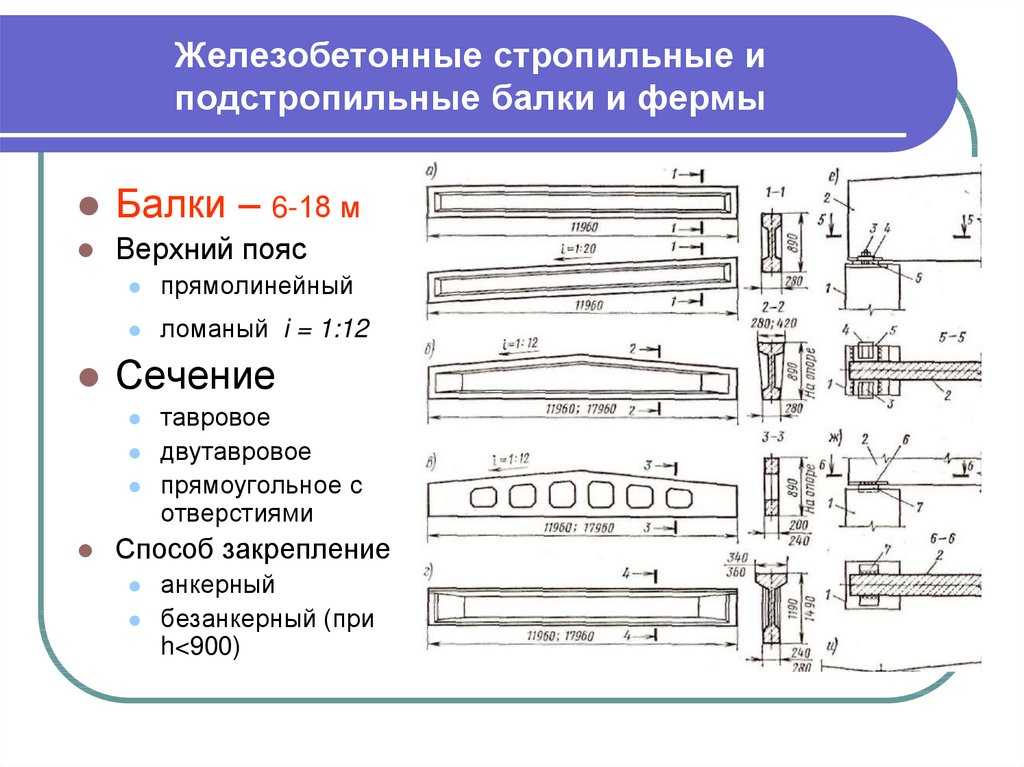
Их масса по ГОСТу от 6 до 50 тонн. Высота в середине пролета обычно 1/6—1/9 длины, а сечение поясов и решетки от 200—240 мм. Ширина верхнего ряда от 1/70 до 1/80 длины, размеры сечения высчитывают по формулам. Нижний равен фактическим размерам верхнего, а высота определяется из фактического расположения вида арматуры. Прочность обеспечивает утолщение в узлах конструкции.
Расшифровка маркировки изделий
Маркировку этих железобетонных изделий обозначают буквами и цифрами, разделенными с помощью дефисов. Арабская цифра в первой связке — номер фермы по порядку, вид и длина в метрах. Числовое значение округляют в большую сторону. Вторая цифра указывает на несущую способность и ее число по порядку, для ферм с напряжением вписывают класс арматурной стали и бетона. В третьей связке описаны особенности применения, таких как сопротивляемость к влиянию агрессивных сред, воздействие которой вызывает коррозию строительного материала в изделии или конструкции (буква С) или сейсмическая устойчивость (7—8 баллов).
Проницаемость бетона отмечают буквами Н (нормальная) и П (пониженная). Если есть дополнительно заложенные элементы их также прописывают.
Для чего используют?
Для сооружений с пролетом больше 18 м применяют железобетонные напряженные изделия с использованием марок бетона специально созданных для этого типа изделий B30, B50. Конструкции сегментного очертания раскосой формы используют при постройке пролетов длиной 24 метра. Если покрытие с малым уклоном устанавливают безраскосные, что позволяет в полной мере использовать межферменное пространство по назначению. Они предназначены для эксплуатации в зданиях с агрессивной, разрушающей конструкции, средой.
Установка таких изделий зависит от характеристик самой постройки.
Чтобы покрыть большепролетные железобетонные конструкции, применяют сборные арочные элементы. Стропильная балка является опорой для подстропильных ферм. Это выполняют, если шаг колонны значительно больше шага несущих элементов. Их используют пролетом 12 м. А в зданиях, которые неотапливаемые, устанавливают треугольные виды железобетонных ферм под кровлю из металлических листов.
К преимуществам ЖБ ферм относят огневую устойчивость, надежность, прочность и долговечность.
Как изготовить конструктивный элемент?
Данное изделие производится строго по ГОСТу с помощью необходимого оборудования.
Основной нормативный документ на который опираются при выпуске таких конструкций из железобетона ГОСТ 20213–89. Процесс производства проходит в одно- и двухъярусных стенд-камерах. Проволоку натягивают гидравлическими домкратами, заливают бетон с помощью бетоноукладчика. Заключительный этап — термическая обработка. Если железобетонное изделие длиной более 9 метров, то следует армировать его с применением напряженного арматурного металлопроката для повышения прочности. Если короче 8, 96 метра, в основном изготавливают ферму с ненапряженной арматурой.
Наиболее легкий процесс изготовления арочного безраскосного типа, внутреннее пространство которого отводится для различных систем коммуникации. Нижний пояс выполняют из арматурных канатов, высокопрочной проволоки или стержневой арматуры.
Если вся технология выполнена правильно, на выходе получают морозостойкий, прочный, водонепроницаемый железобетонный продукт с устойчивостью к коррозии и трещинам.
Beliebtester Live Sex Chat with Free-Cams bei BongaCams
Sexyste Новичок
#минет
#шванцлушен
#fickende paare
#genießend
Mehanikkk1342s Чат
#анальныйшпиль
#камшоу
#фикен
#мастурбация
LinaKisas Чат
#аршлеккен
#бласен
#сперма в муши
#fickmaschinen
Чат SEXNoomads
#sperma im Gesicht
#бутерброд
#фуссфикен
#анмачен
Давайте знакомиться)))
#эйерлушен
#раухен
#Cam2Cam Prime
squirt/555TKNS♥Я ВАША ИДЕАЛЬНАЯ КОРОВА LOL♥СОВЕТ 5 ДЛЯ MUUU ♥Давай, поиграй с этой крошечной киской♥[none] ТРАХНИ МОЮ ВЛАЖНУЮ КИСКУ♥ PVT O
#блазен
#камшоу
#экшн с дилдо
#träumenn
— Цель: ♥дрочить♥Я жажду наслаждений и только у тебя есть то, что мне так нравится.
Ты дашь мне? Ну, я сквирт
#танзен
#экшн с дилдо
#дрочка
#König des Raums
нефтяная выставка 2000 677 1323
#харт фикен
#раухен
#ловенс
Чат FalakTalebs
#айерлекен
#sperma im Gesicht
#дрочка
#reiben
949 до стриптиз, ледовое шоу 222тк, киска 95тк, сквирт 499тк, дилдо в киске 459тк!!!
#танзен
#дилдофикен
#фуссфикен
#strippen
Doll4yous Чат
#любимая машина
#мастурбация
#муширайбен
#lovense
Привет! My Lovense работает от 2 токенов, подписывайтесь и ставьте лайк! ❤️
#по фикен
#траумен
#раухен
#Испанский
Instagram tylerjesusmeza thle girl is virgen for ass 18 year 400 for hard fuck 600 for cum come onm
Качественные секс-шоу в HD+
#камшоу
#анмачен
#Englisch
Голые в приватах ♥ СОВЕТЫ ТОЛЬКО В БЕСПЛАТНЫЙ ЧАТ НЕ в личку !!!♥ Всем хорошего настроения! «15000 — нужно: 0 собрал, 15000 осталось
#träumen
#раздеть
#Шпиле
#Vibe with Me
привет=) 505 ток пре чаевые перед пвт в паблик чат.
Уровни Lovense 15, 50, 100, 300, 500, 1000 и специальные команды 111 случайных, 2
#глубокая глотка
#дилдофикен
#экшн с дилдо
#anmachen
Всем привет) Я Дарина ❤ LOVENSE из 2 тока, рандом — 101 ток, любимая вибрация -200 ток ❤
#камшоу
#шванцлушен
#Руссищ
ОгонЕчеКККс Чат
#камшоу
#фуссфикен
#зайгефройдиг
#муширайбен
Привет) Ловенс от 5 ток.
Любимый вибро 151 ток.
Стриптиз через [нет] ток
#айерлекен
#рейбен
#Анальный Фистинг
:heart5❤️ привет, ❤️Я Милана,✨ поставь любовь! Lovens от 5 +❤️ ТОЛЬКО Полный Приват. ❤️ДО ПРИВАТА 333 ❤️❤️❤️ 9Полное приватное или только групповое, PM перед приватным [нет] Эксклюзивное шоу Taanni! ❤️
#аршфиккен
#бласен
#дилдофикен
#бутерброд
ПЫТАЙ МЕНЯ❤️ Время мокрого оргазма 666Tkns ❤️ Управляй моими игрушками 888Tkn❤️Сделай меня сумасшедшим и счастливым, большой оргазм 1111 Tkns❤️Fuck Puss
#танзен
#вичсен
#Anales Fisting
Lovence от 2 токенов. Игрушка управления 5 мин 650 жетонов 🙂
голый в масле [нет] ток
#эйерлушен
#шванцлушен
#мастурбация
#HD+
мы тут новенькие, очень хотим с вами поиграть) много сквирта осталось 628
#шванцлучен
#Aufnehmbar
Привет. Мы Лиза и Катя. Не делайте ничего для токенов в pm.
#раухен
#weibliche dominanz
#König des Raums
Это новый день для нас, чтобы иметь все Пожалуйста, пожалуйста, мне Потратьте всю свою любовь на то, чтобы я чувствовал себя настоящим для вас
[
Интерактив (Lovense, Fickmaschine и т. д.)
#аршфиккен
#куннилингус
#ловенс
_Kirloves Чат
#арш-цу-Мунд
#бдсм
#handjob
НА НОВЫЙ ГОД ПОДАРОК АНЕ ❤️ 10844 собрано, осталось 4155
ЛЮБИМАЯ ВИБРО: 27 101 555
777 ЖЕТОНОВ МАКС. ВИБРО 200 СЕКУНД
#eierlutschen
#бутерброд
#lutschen
Прогулка с Lovense ❤️Есть секс-игрушки (Domi) (Lovens) от 2-х жетонов/не жалей меня❤️
#genießend
#дрочка
#анмачен
#лекен муши
:big_107 двойной сквирт на лицо :big_107
4444 — обратный отсчет
4081 — собрано
363 — осталось до шоу
#глубокая глотка
#genießend
#muschilecken
#HD+
hornycupps Чат
#айерлекен
#абспритцен
#лючен
#cunnilingus
Чат HellMors
#Vibe with Me
Чат Kristi-21s
#экшн с дилдо
#бутерброд
#strippen
привет!
я хипси
Со мной горячо и вкусно)
Любимая вибрация/50❤️
В полном привате самое горячее
Камера-88
#минет
#чаттен
#танзен
#träumen
Эллидис Чат
#Азия-Массаж
#абспритцен
#экшн с дилдо
#Русский
чат bobmarly247s
#шванцлучен
#genießend
#куннилингус
#Spiele
любимые вибрации 88 и 101 (влажно-мокро)
Для уютного дома с камином [нет] осталось [нет]
За подписку СИСЬКИ^.
#сперма в муши
#вюрген
#muschilecken
❤️ Привет, меня зовут Мила. Ловенс и доми от 1 токена. ПМ 16 жетонов, жопа 60 жетонов, Сиськи 88 жетонов, Киска и жопа 150
Достижения Модели Ферм для ЖБК
Открытый журнал гражданского строительства
Том 2 № 3 (2012 г.), идентификатор статьи: 22985, 7 стр. , Hariton Xenidis, Panos Lazaridis, Andreas Diamantopoulos, Periklis Lambrou, Yannis Arethas
Факультет гражданского строительства, Университет Аристотеля в Салониках, Салоники, Греция
Электронная почта: [email protected], [email protected], [email protected]
Поступила в редакцию 9 апреля 2012 г.; пересмотрено 10 мая 2012 г.; принято 24 мая 2012 г.
Ключевые слова: Железобетонная конструкция; модель фермы; Учредительный закон; Материальные и геометрические нелинейности; Растрескивание бетона; Усиление Выход; предел прочности бетона на сжатие; Пластиковая петля; ЖБ колонна локализации; Изгиб внутренних бетонных стоек; Глобальная нестабильность
РЕФЕРАТ
Представлены достижения для ферменных моделей железобетонных конструкций, разработанных в предыдущие годы: 1) две конститутивные модели, двухосная и трехосная, основаны на регулярных фермах, стержни которых подчиняются нелинейным одноосным законам σ-ε моделируемого материала; обе модели сопоставлены с результатами испытаний и показывают зависимость коэффициента Пуассона от кривизны закона σ-ε; 2) конечный элемент фермы использовался в нелинейном статическом и динамическом анализе плоских железобетонных рам; она сопоставлена с результатами испытаний и в простой форме описывает формирование пластических шарниров; 3) Благодаря очень простой геометрии фермы можно легко написать уравнения равновесия и легко обновить матрицу жесткости, как по отношению к деформированной ферме, так и на каждом шаге статического добавочного нагружения или на каждом временном шаге динамический анализ, чтобы учесть геометрические нелинейности. Таким образом, ограничение железобетонной колонны интерпретируется как эффект структурной устойчивости бетона. Выявлена существенная роль поперечной арматуры в предотвращении за счет ее близкого расположения и достаточного количества коробления внутренних продольных железобетонных стоек, что привело бы к глобальной неустойчивости железобетонной колонны; 4) Предложенная модель фермы является статически неопределимой, поэтому она обладает некоторыми особенностями, которых нет в модели «подкос и связь».
1. Введение
В 1967 г. в пионерской работе [1] Д. Нго и А. С. Скорделис представили подробную модель конечных элементов для железобетонной балки, в которой отдельные конечные элементы используются для бетонной и стальной арматуры. Нелинейность материала арматуры может быть легко описана нелинейным одноосным законом σ-ε стержневого элемента. Однако трудно представить нелинейное двухосное или трехосное поведение напряжения-деформации бетона или любого другого материала. Соответствующие проблемы обсуждаются в двух актуальных отчетах по нелинейному анализу железобетонных конструкций методом конечных элементов, в одном из которых П. Г. Берган и И. Холанд в 1979 [2] и еще один в специальной публикации ASCE в 1982 г. [3], написанной специалистами в этой области под руководством А. К. Скорделиса. Кроме того, трудности, возникающие при применении конечных элементов к нелинейным задачам, обсуждались в серии из трех конференций F.E. No. Mech. (Конечные элементы в нелинейной механике), организованной Дж. Х. Аргирисом в Институте статики и динамики Штутгартского университета, Германия, в 1978, 1981, 1984 годах [4].
Для описания нелинейного двухосного или трехосного поведения напряжения-деформации конструкции с помощью метода конечных элементов необходимо разработать определяющие модели конструкционных материалов, чтобы их можно было воплотить в отдельных конечных элементах. Усилия по разработке таких конститутивных моделей предпринимались многими исследователями, в т.ч. модели пластичности В. Ф. Чена [5] и З. Мроза [6], модель пластического разрушения З. П. Базанта [7], а также более практические работы Д. Дарвина [8] и К. И. Уиллама [9].], для нелинейного, двухосного и трехосного соответственно напряженно-деформированного поведения бетона.
В 1977 г. [10] Н. Дж. Берт и Дж. В. Дугилл представили конститутивную модель со случайной сетью, чтобы описать нелинейный двухосный закон напряжения-деформации материала, и заметили, что эквивалентные результаты могут быть получены с использованием простых регулярных сетей. Применяя эту идею, П. Г. Пападопулос разработал в 1984 и 1986 гг. [11, 12] двухосную и трехосную конститутивную модель сети, основанную на правильном плоском восьмиугольнике и правильном пространственном ромбическом додекаэдре соответственно, в которых стороны и диагонали являются стержнями, подчиняющимися нелинейные одноосные σ-ε закономерности моделируемого материала. Результаты вышеуказанных сетевых конститутивных моделей были найдены в удовлетворительном приближении к соответствующим опубликованным результатам испытаний [13-15].
Фермы использовались не только в конститутивных моделях, но и в конечных элементах конструкций. В 1978 г. [16] Э. Абси в своей «теории эквивалентности» утверждал, что простые конечные элементы фермы дают эквивалентные результаты с обычными более сложными континуальными конечными элементами. Эта идея была распространена на задачи с материальными нелинейностями и на нелинейный статический и динамический анализ плоских железобетонных рам П. Г. Пападопулосом [17,18]. Предложен простой конечный элемент фермы, основанный на плоском прямоугольнике, в котором все стороны и диагонали являются стержнями, подчиняющимися нелинейным одноосным законам σ-ε бетона или стали. Таким образом, нелинейное двухосное напряженно-деформированное поведение элемента описывается простым способом, таким образом, воплощение определяющего закона в отдельных конечных элементах больше не требуется. Результаты нелинейного статического анализа на циклическое нагружение, а также нелинейного сейсмодинамического анализа простых плоских железобетонных рам с помощью предлагаемого ж/б элемента фермы были сопоставлены с соответствующими опубликованными результатами испытаний и найдены в удовлетворительной аппроксимации с ними [19]. ,20]. Поскольку стержни предлагаемого конечного элемента включают в себя основные нелинейности материала бетона и стали, то есть растрескивание бетона при растяжении и предел прочности при сжатии, а также предел текучести арматуры при растяжении, предлагаемая модель фермы может простым способом описать формирование пластиковых петель в ж/б раме.
Впоследствии были разработаны некоторые другие версии идей Э. Абси для конечных элементов фермы для плоских конструкций под разными названиями, но все они похожи друг на друга, например. «аналогия фермы» в 1997 [21] для стальных конструкций, «решетчатая модель» в 1997 г. [22] и «модель сосредоточенных напряжений» в 2002 г. [23], последние две для железобетонных конструкций.
В 1987 г. [24] Й. Шлайх изобрел так называемую модель «распорно-связной», которая представляет собой статически определимую модель фермы, состоящей из бетона и стальных стержней. Эти стержни включают в себя основные материальные нелинейности железобетонной конструкции. Таким образом, модель «распорка и связь» может эффективно описывать основные напряженно-деформированные состояния железобетонной конструкции, то есть изгиб, сдвиг и даже кручение в 3D, таким образом, она зарекомендовала себя как очень полезный практический инструмент в анализе и проектирование железобетонных конструкций.
Модель «распорки и связи» получила дальнейшее развитие другими исследователями, такими как Т. Т. Хсу в 1993 г. [25], Ф. Дж. Веккио и М. П. Коллинз в 1993 г. [26], а также комитетом ASCE-ACI по сдвиг и кручение в 1998 г. [27].
Предлагаемая здесь модель фермы является статически неопределимой конструкцией, поэтому она демонстрирует некоторые особенности, которые не удовлетворяются статически определимой моделью «распорки и связи»:
1) Она может описывать эффект поперечного расширения (коэффициент Пуассона).
2) Он учитывает геометрическую нелинейность путем написания уравнений равновесия и обновления матрицы жесткости как по отношению к деформированной ферме, так и на каждом шаге статического добавочного нагружения или на каждом временном шаге динамического анализа. Это легко достигается благодаря очень простой геометрии фермы.
По этой предложенной модели фермы, которая включает в себя геометрические нелинейности, ограничение железобетонной колонны интерпретируется как эффект структурной устойчивости бетона [28-30].
И, кроме уже известных ролей поперечной арматуры [31-33] (т.е. передача сдвига, уменьшение выкрашивания бетона, предотвращение коробления продольной арматуры, повышение жесткости при сжатии, прочности и пластичности ограниченного бетонного ядра ), еще одна важная роль поперечной арматуры раскрывается в предлагаемой модели фермы с конструктивной неустойчивостью, а именно в замедлении и даже предотвращении за счет ее близкого расположения и достаточного количества потери устойчивости внутренних продольных бетонных стоек, что привело бы к глобальной неустойчивости. ЖБ колонны.
Результаты применения предложенной модели с неустойчивостью конструкции при ограничении железобетонных колонн удовлетворительно соответствуют требованиям норм [34-36] в отношении расстояния и количества поперечной арматуры, которые, в свою очередь, основаны на результаты анализов тоже.
Далее более подробно будут описаны некоторые из достижений предложенных выше моделей ферм для нелинейного анализа конструкций, в основном железобетонных конструкций, предложенных в предыдущие годы.
2. Определяющие модели ферм
Были разработаны двухосная и трехосная определяющие модели нелинейного закона деформации материала [11,12], основанные на правильном плоском восьмиугольнике и правильном пространственном ромбическом додекаэдре соответственно. в котором стороны и диагонали являются стержнями, подчиняющимися нелинейному одноосному закону σ-ε моделируемого материала. Таким образом, простым образом, нелинейными одноосными законами σ-ε стержней описывается нелинейное двухосное или трехосное напряженно-деформированное поведение всей фермы. Результаты вышеуказанных конститутивных моделей ферм для различных историй нагружения были найдены в удовлетворительном приближении к соответствующим опубликованным результатам испытаний [13-15]. Обе вышеприведенные определяющие модели фермы показывают зависимость значения коэффициента Пуассона ν от кривизны κ нелинейного одноосного закона σ-ε рассматриваемого материала, как показано на рисунке 1. 9.0003
3. Конечный элемент фермы для плоского железобетонного каркаса
Предложен конечный элемент фермы для балок плоского железобетонного каркаса, основанный на прямоугольнике, в котором все стороны и диагонали являются стержнями, подчиняющимися нелинейным одноосным σ-ε законам бетона или стали, как показано на рисунке 2. Закон σ-ε бетонных стержней включает растрескивание при растяжении, предельную прочность на сжатие, а также правила нагружения-разгрузки после текучести при сжатии. Принимая во внимание, что закон σ-ε стального стержня включает в себя предел прочности на растяжение и сжатие, а также правила нагрузки-разгрузки после растяжения или сжатия.
4. Определение сечений стержней
В предложенном выше конечном элементе фермы для балок плоских железобетонных рам площади поперечных сечений стальных стержней разумно и легко определяются как суммы сечений соответствующих стальных арматурных стержней. Принимая во внимание, что для определения площадей поперечных сечений A 1 , A 2 , A 3 бетонных стержней элемента фермы, как показано на рисунке 3 (b), мы должны сравнить его с соответствующим элемент непрерывной бетонной балки на рисунке 3 (а), что касается трех репрезентативных состояний напряженно-деформированного состояния в линейной упругой области. И мы выбрали в качестве таких характерных состояний чистый изгиб, ограниченную осевую деформацию, а также ограниченную поперечную деформацию.
Для чистого изгиба, показанного на рисунке 3(c), угол кривизны элемента балки равен где, тогда как для элемента фермы
где. Комбинируя приведенные выше уравнения, мы получаем.
Рис. 1. Зависимость коэффициента Пуассона ν от кривизны κ нелинейного одноосного σ-ε закона материала. (а) Металл κ = 0 г v = 1/3; (b) Геологический материал, т.е. бетон κ 0 г ν > 1/3.
Рис. 2. (a) Конечный элемент фермы для балки плоской железобетонной рамы с бетонными и стальными стержнями; (б) Нелинейный одноосный закон σ-ε бетонных стержней; (c) Нелинейный одноосный закон σ-ε стальных стержней.
Рисунок 3. Сравнение характеристических напряженно-деформированных состояний элемента бетонной балки и соответствующего элемента фермы для определения сечений бетонных стержней. а) элемент бетонной балки; b) соответствующий элемент фермы; в) чистый изгиб; (d) Ограниченное осевое сжатие.
Теория упругости дает ограниченную осевую деформацию.
Для, таким образом где и. В соответствующем состоянии элемента фермы, показанном на рис. 3(г), имеем
где и .
Из комбинации приведенных выше уравнений получаем
Из аналогичных соображений для ограниченной поперечной деформации получаем.
Очевидно, что при стремлении угла θ к нулю, θ → 0 сечения стремятся к A 3 → и A 2 →.
5. Нелинейный статический анализ
Инкрементальное нагружение конструкции предпочтительно выполнять с помощью контроля деформации, который является более стабильной процедурой, чем контроль напряжения. Нелинейности материала учитываются изменением модулей упругости Е стержней при нагружении. Принимая во внимание, что для учета геометрических нелинейностей записываются уравнения равновесия и обновляется глобальная матрица жесткости, как по отношению к деформированной ферме, так и на каждом шаге добавочного нагружения. Матрица локальной жесткости стержня в 2D, состоящая из упругой и геометрической частей, равна:
где A сечение, l o недеформированная длина, l существующая длина, N осевая сила и c x , c y направляющие косинусы стержня.
Принимая во внимание, что глобальная матрица жесткости фермы имеет вид:
где B Булева матрица связей и n b количество стержней фермы.
На основе предложенного алгоритма была разработана очень короткая компьютерная программа, содержащая всего около 200 инструкций FORTRAN, для нелинейного статического анализа модели фермы плоской железобетонной рамы.
6. Нелинейный динамический анализ
Сосредоточенная масса назначается каждому свободному узлу фермы. Предполагается нулевое демпфирование и нулевые начальные скорости. Полученная начальная задача:
, где вектор состояния есть r, v положений и скоростей узлов и c определяющих переменных стержней, решается пошаговым алгоритмом трапециевидного правила, который совпадает с алгоритмом Ньюмарка постоянного среднего ускорения:
в сочетании с методом предиктор-корректор с двумя коррекциями на шаг, PE(CE) 2 [37]. Таким образом, нет необходимости решать алгебраическую систему на каждом шаге алгоритма.
Критерий устойчивости алгоритма — рад, а критерий точности — рад, что определяет выбор длины временного шага алгоритма Δt.
Верхнюю границу нормальных частот можно найти из нормы матрицы M – 1 K, где M матрица масс и K матрица жесткости конструкции:
На основе предложенного алгоритма была разработана очень короткая компьютерная программа, содержащая всего около 150 инструкций FORTRAN, для нелинейного динамического анализа модели фермы железобетонной рамы.
7. Приложения к анализу простых плоских железобетонных рам
Предложенный выше конечный элемент фермы для плоских железобетонных рам, а также предложенные алгоритмы нелинейного статического и динамического анализа были применены к нелинейному статическому анализу простой плоскости. ЖБ каркаса для циклического нагружения [17], а также к нелинейному динамическому сейсмическому анализу простого плоского ЖБ каркаса [18]. Результаты этих анализов находятся в удовлетворительном приближении к соответствующим опубликованным результатам испытаний [19].,20].
Поскольку нелинейные одноосные законы σ-ε стержней предлагаемой модели фермы включают в себя все основные материальные нелинейности железобетонной конструкции, то есть растрескивание при растяжении и предел прочности при сжатии бетона, а также текучесть стальной арматуры при растяжении , формирование пластических шарниров в железобетонной раме простым способом описывается, как показано на рисунке 4.
8. Применение к ограничению железобетонной колонны модели фермы, записываются уравнения равновесия и обновляется матрица жесткости, как по отношению к деформированной ферме, так и на каждом шаге статического добавочного нагружения или на каждом временном шаге динамического анализа. Это легко достигается благодаря очень простой геометрии фермы.
Поскольку предлагаемая модель фермы включает в себя геометрические нелинейности, она интерпретирует ограничение железобетонной колонны как эффект структурной устойчивости бетона [28-30].
На рисунке 5(a) показана осевая σ-ε диаграмма сжатия ограниченной железобетонной колонны. Наблюдается ранний небольшой спад напряжения, что связано с локальной неустойчивостью из-за выкрашивания (выпучивания) наружного бетона. При дальнейшем увеличении нагрузки, предпочтительно за счет контроля деформации, при значительном значении осевой деформации сжатия напряжение σ внезапно падает до нуля, что является очевидным признаком общей нестабильности конструкции, наблюдаемой в экспериментах и подтвержденной предложенной моделью фермы. тоже.
На рисунке 5(b) показана часть ограниченной железобетонной колонны между двумя последовательными наборами поперечной арматуры. Продольное армирование опущено для простоты. По мере постепенного увеличения сжимающей осевой нагрузки N происходит боковое расширение бетона. При значительных сжимающих осевых деформациях из-за большого бокового расширения бетона возникает текучесть поперечной арматуры при растяжении, что означает
Рис. модель фермы. «……» треснувший бетон. «——» армирование при растяжении. «//////» жесткие детали. Пластиковые петли «ph».
(a) (b)
Рис. 5. (a) Осевая σ-ε диаграмма сжатия ограниченной железобетонной колонны. 1. Раннее небольшое падение напряжения из-за отслаивания наружного бетона. 2. При значительной величине сжимающей осевой деформации напряжение σ резко падает до нуля, что является признаком глобальной неустойчивости конструкции; (b) Часть замкнутой железобетонной колонны между двумя последовательными комплектами поперечной арматуры. 1. Отслаивание наружного бетона. 2. Поперечная арматура при растяжении. 3. Продольные бетонные трещины. 4. Продольные бетонные стойки.
дополнительное боковое расширение бетона. Так образуются широкие продольно-вертикальные бетонные трещины, а между такими последовательными бетонными трещинами образуются внутренние продольно-вертикальные бетонные стойки, которые имеют тенденцию к выпучиванию, что приводит к глобальной неустойчивости железобетонной колонны.
Помимо уже известных функций поперечной арматуры в железобетонной колонне [31-33] (т.е. передача сдвига, уменьшение выкрашивания бетона, предотвращение коробления продольной арматуры, повышение осевой жесткости при сжатии, прочности и пластичности ограниченного бетона стержень), еще одна существенная роль поперечной арматуры раскрывается в предлагаемой модели фермы с конструктивной неустойчивостью, а именно замедление и даже предотвращение ее близким шагом s и достаточной величиной ρ (механическое соотношение) выпучивания указанной внутренней продольной арматуры. вертикальные бетонные стойки, что привело бы к глобальной нестабильности ЖБ колонны.
Результаты применения предложенной модели фермы с неустойчивостью конструкции к ограничению железобетонных колонн были найдены в удовлетворительном приближении с соответствующими требованиями норм и правил [34-36] в отношении шага s и механического отношения ρ поперечной арматуры ; эти требования, в свою очередь, также основаны на результатах испытаний.
9. Выводы
Представлены некоторые достижения для ферменных моделей конструкций, в основном железобетонных конструкций, которые были разработаны в предыдущие годы и найдены в удовлетворительном приближении к результатам испытаний и требованиям СНиП:
1) Н. Дж. Берт и Дж. У. Дугилл разработали в 1977 г. [10] конститутивные модели случайных сетей и заявили, что эквивалентные результаты могут быть простым способом получены с помощью регулярных сетей. Эта идея была реализована в 1984 г. [11] и 1986 г. [12] двумя сетевыми конститутивными моделями, двухосной и трехосной, основанными на правильном плоском восьмиугольнике и правильном пространственном ромбододекаэдре соответственно, в которых стороны и диагонали являются стержнями, подчиняющимися нелинейный одноосный закон σ-ε моделируемого материала. Обе модели показывают зависимость коэффициента Пуассона от кривизны по нелинейному одноосному закону σ-ε материала.
2) Э. Абси в 1978 г. [16] в своей «теории эквивалентности» утверждал, что простые конечные элементы фермы дают эквивалентные результаты с обычными более сложными континуальными конечными элементами. Эта идея была распространена в 1988 году [17,18] на конструкции с нелинейностью материала и применялась, в частности, к нелинейному статическому и динамическому анализу плоских железобетонных рам. Поскольку отдельные стержни предложенного конечного элемента фермы включают в своих одноосных законах σ-ε основные материальные нелинейности железобетонной конструкции, то есть растрескивание бетона при растяжении, предел текучести арматуры при растяжении, а также предел прочности бетона на сжатие. , образование пластиковых петель в ж/б раме можно описать простым способом.
3) По сравнению с моделью «распорка и связь» для железобетонных конструкций, изобретенной J. Schlaich в 1987 г. [24] и развитой другими исследователями, которая оказалась очень эффективным инструментом при анализе железобетонных конструкций, предлагаемая здесь модель фермы отличается тем, что она является статически неопределимой, тогда как модель «распорка и связь» является статически определимой. Итак, предлагаемая модель фермы имеет некоторые особенности, которые не встречаются в модели «подкос и связь»: а) Она может описывать эффект бокового расширения (коэффициента Пуассона). b) Он учитывает геометрическую нелинейность путем написания уравнений равновесия и обновления матрицы жесткости как по отношению к деформированной ферме, так и на каждом этапе нелинейного статического или динамического анализа. Так, интерпретируется в 1999 [31] ограничение железобетонной колонны как эффект структурной устойчивости бетона. И выявил значительную роль поперечной арматуры, которая замедляет и даже предотвращает, ее близкое расположение и достаточное количество, коробление внутренних продольных бетонных стоек, что привело бы к глобальной нестабильности железобетонной колонны.
ССЫЛКИ
- Д. Нго и А. С. Скорделис, «Конечно-элементный анализ железобетонных балок», журнал ACI, Vol. 64, 1967, стр. 152-163.
- Берган П.Г. и Холанд И. Нелинейный анализ бетонных конструкций методом конечных элементов // Компьютерные методы в прикладной механике и технике. 17-18, 1979, стр. 443-467. doi:10.1016/0045-7825(79)
-6
- А. К. Скорделис, редактор Целевого комитета ASCE по бетонным и каменным конструкциям, «Современный отчет по конечно-элементному анализу железобетона», Специальная публикация ASCE , 1982.
- Дж. Х. Аргирис, организатор международных конференций F.E.No.Mech. (Конечные элементы в нелинейной механике). Институт статики и динамики Штутгартского университета, Германия, I.30 августа – 1 сентября 1978, II. 25-28 августа 1981 года. III. 10–13 сентября 1984 г.
- В. Ф. Чен и Э. К. Тинг. «Основные модели бетонных конструкций», Журнал отдела инженерной механики ASCE, Vol. 106, № 1, 1980, стр. 1-19.
- Мроз З., Норрис В.А., Зенкевич О.К. Применение модели анизотропного упрочнения при анализе упругопластической деформации грунтов // Геотехника. 29, 1979, стр. 1-34. doi:10.1680/geot.1979.29.1.1
- З. П. Базант и С. С. Ким, «Теория пластического разрушения бетона», Журнал отдела инженерной механики ASCE, Vol. 105, № 3, 1979, стр. 407-428.
- Д. Дарвин и Д. А. Пекнольд, «Анализ циклического нагружения железобетонных конструкций», Компьютеры и конструкции, Vol. 7, № 1, 1977, стр. 137-147. doi: 10.1016/0045-7949(77)
-2
- К. Дж. Уиллам и Э. П. Варнке, «Конструктивная модель трехосного поведения бетона», Труды IABSE, Отчет по проектированию конструкций 19, Раздел III, 1975 г., стр. 1- 30.
- Н. Дж. Берт и Дж. В. Дугилл, «Прогрессирующий отказ в модельной неоднородной среде», Журнал отдела инженерной механики ASCE, Vol. 103, 1977, стр. 365-376.
- Пападопулос П. Г., «Конструктивная модель двухосной сети», Журнал инженерной механики ASCE, Vol. 110, № 3, 1984, стр. 449-464. doi:10.1061/(ASCE)0733-9399(1984)110:3(449)
- Пападопулос П.Г. Конститутивная модель трехосной сети // Компьютеры и структуры. 23, 1986, стр. 497-501. doi:10.1016/0045-7949(86)
-3
- Купфер Х.Б., Хильсдорф Х.Д. и Руш Х. Поведение бетона при двухосных напряжениях // Журнал ACI. 66, № 8, 1969, стр. 656-666.
- Р. Паланисвами и С.П. Шах, «Взаимосвязь разрушения и напряжения и деформации бетона при трехосном сжатии», Журнал структурного подразделения ASCE, Vol. 100, 1974, стр. 901-916.
- Р. Скавуццо, Т. Станковски, К. Герстл и Х.-Ю. Ко, «Кривые напряжения-деформации для бетона при многоосных нагрузках», Университет Колорадо, Боулдер, 1983.
- Э. Абси, «Методы численного расчета эластичности», Eyrolles, Париж, 1978.
- П. Г. Пападопулос, « Нелинейный статический анализ железобетонных рам с помощью сетевых моделей, Достижения в инженерном программном обеспечении, Vol. 110, № 3, 1988, стр. 114-122. doi:10.1016/0141-1195(88)
-1
- Пападопулос П.Г., Караяннис К.Г. Сейсмический анализ железобетонных каркасов с помощью сетевых моделей // Компьютеры и конструкции. 28, № 4, 1988, стр. 481-494. doi:10.1016/0045-7949(88)
-3
- К. Стилианидис и Г. Пенелис, «Экспериментальное исследование голых и заполненных стеной одноэтажных каркасов при циклической сдвиговой нагрузке», 7-я Греческая конференция по бетону, том . 2, Патра, 1985, стр. 47-55.
- П. Идальго и Р. В. Клаф, «Исследование железобетонной рамы на симуляторе землетрясения», Отчет EERC 74-13, Калифорнийский университет, Беркли, 1974.
- С. К. Гоэл, Б. Стоядинович и К. Х. Ли, «Аналогия ферм для стальных моментных соединений», Инженерный журнал, второй квартал 1997 г., стр. 43-53.
- Э. Шланген и Э. Дж. Гарбоци, «Моделирование разрушения бетона с использованием решетчатых моделей: вычислительные аспекты», Инженерная механика разрушения, Том. 57, № 2-3, 1997, стр. 319-332. doi:10.1016/S0013-7944(97)00010-6
- Ф. Фратернали, М. Анджелило и А. Фортунато, «Метод сосредоточенных напряжений для плоских задач упругости и приближение дискретной непрерывной среды», Международный журнал твердых тел и конструкций, Том. 39, 2002, стр. 6211-6240. doi:10.1016/S0020-7683(02)00472-9
- J. Schlaich, K. Schäfer и M. Jennewein, «На пути к последовательному проектированию конструкционного бетона», специальный отчет журнала PCI, Vol. 32, № 3, 1987, стр. 75-150.
- Т. Т. С. Хсу, «Единая теория железобетона», CRC Press, 1993. 113, 1993, стр. 3590-3610. дои: 10.1061 / (АССЕ) 0733-9445(1993)119:12(3590)
- Комитет ASCE-ACI 445 по сдвигу и кручению, «Современные подходы к расчету структурного бетона на сдвиг. Отчет о состоянии дел», Журнал структурной инженерии ASCE, Vol. 119, № 12, 1998, стр. 1375-1417.
- П. Г. Пападопулос и Х. К. Ксенидис, «Модель фермы с неустойчивостью конструкции для удержания бетонных колонн», Журнал EEE (European Earthquake Engineering), часть 2, 1999 г., стр. 57-79.
- П. Г. Пападопулос, Х. Ксенидис, К. Караяннис, А. Диамантопулос и П. Ламброу, «Удержание бетонной колонны, интерпретируемое как эффект структурной устойчивости», 6-я конференция GRACM (Греческая ассоциация вычислительной механики), Салоники, 19-21 июня 2008 г.
- П. Г. Пападопулос, Х. Ксенидис, Д. Пласатис, П. Киусис и К. Караяннис, «Стабильность бетона, достигаемая за счет удержания в железобетонной колонне», 12-я Международная конференция по вычислениям в области гражданского строительства, строительства и окружающей среды, Координатор Б.Х.В. Топпинг, Мадейра, Португалия, 1–4 сентября 2009 г.
- К. Парк, М. Дж. Н. Пристли и В. Д. Гилл, «Пластичность квадратных бетонных колонн», Журнал структурного подразделения ASCE, Vol. 108, № 4, 1982, стр. 929-9.50.
- С. Уотсон, Ф. А. Зан и Р. Парк, «Ограничивающая арматура для бетонных колонн», Журнал структурной инженерии ASCE, Vol. 120, № 6, 1984, стр. 1798-1849.
- Дж. Б. Мандер, М. Дж. Н. Пристли и Р. Парк, «Теоретическая модель напряжения-деформации для замкнутого бетона», Журнал структурной инженерии ASCE, Vol. 114, № 8, 1988, стр. 1804-1826. doi:10.1061/(ASCE)0733-9445(1988)114:8(1804)
- Единые строительные нормы и правила 2, «Положения о проектировании конструкций», глава 19. Бетон, 19.2.1. Железобетонные конструкции, сопротивляющиеся силам, вызываемым сейсмическими движениями 19.2.14. Элементы рамы, подверженные изгибу и осевой нагрузке, 1994, стр. 237-239.
- Новозеландские стандарты 3101, «Свод правил по проектированию бетонных конструкций», глава 17, Элементы, подвергающиеся изгибающим и осевым нагрузкам, Дополнительные сейсмические требования, 1989 г.
- Еврокод 8, «Проектирование сейсмостойких конструкций», часть 1-3.