Содержание
Растворный узел для удобрений своими руками
с миксером или без миксера
какой мощности насос
эффективная конструкция гидромешалки
пропускная способность трубопроводов и фильтров
эффективная гидравлическая схема
с фильтрами или без
система дозирования
слив остатков и система промывки
химстойкие комплектующие, где это критично
состав растворного узла
какие ёмкости использовать для мобильных РУ
металлический каркас для мобильных РУ
где можно купить почти все комплектующие для растворного узла
Получить консультацию или заказать комплектующие
Ответить на 5 вопросов и получить предложение на растворный узел
4,5 м³ до 120 м³ и больше
собираем с 2011 года
С 2011 года компания Агросектор специализируется на изготовлении растворных узлов, а также их монтаже, модернизации и поставке комплектующих.
Наши узлы увеличивают производительность работы опрыскивателей в 2-3 раза.
Среди наших клиентов есть хозяйства, которые сами для себя изготавливают растворный узел и обращаются к нам за консультацией и поставкой комплектующих для сборки растворного узла своими руками. Это выгодно, если у хозяйства есть в штате специалисты, которые могут организовать на месте сборку такого агрегата.
Также нас просят модернизировать растворные узлы, не устраивающие хозяев по причине низкой производительности или надежности.
В данной статье мы обобщили самые распространенные ошибки при сборке растворного узла для удобрений своими руками и дали конкретные рекомендации как их избежать. Мы осветили вопросы:
- миксером или без миксера строить растворный узел
- какой мощности насос выбрать
- эффективная конструкция гидромешалки
- пропускная способность трубопроводов и фильтров
- эффективная гидравлическая схема
- с фильтрами или без
- система дозирования
- слив остатков и система промывки
- химстойкие комплектующие, где это критично
Если же вас интересует готовый растворный узел в сборе, то подробнее можете ознакомиться с моделями и описанием наших узлов здесь.
Список комплектующих, которые вы можете приобрести у нас здесь.
1. С миксером или без миксера
Нередко, для экономии, в растворном узле производители или сами хозяйства устраивают перемешивание сразу в накопительной ёмкости, с помощью насоса, который создаёт движение воды. Обычно это обустраивают так. На бочке насос подаёт с одной стороны, а забирает с другой. В это время в бочку засыпается удобрение. В качестве ёмкостей применяют пластиковые от 5м3 до 30м3 и жд цистерны 60м3.
При небольших объёмах ёмкости — по нашему опыту это до 1000л — система гидроперемешивания отлично работает. Если же ёмкость большая — 3м3, 5м3, 10м3 и более, то даже при правильном обустройстве системы гидроперемешивания возникают следующие негативные последствия:
— при размешивание сухих препаратов удобрения не растворяется до конца, образуется осадок.
— низкая скорость растворения. Для приготовления одной порции вместо 20-30 минут может уйти 2-3 часа.
— неоднородный характер раствора. Т.е. некачественный раствор.
Т.е. некачественный раствор.
— осадок забивает фильтры, повышает износ насоса, засоряет форсунки опрыскивателей. При наличии фильтра – он быстро засоряется. При отсутствии фильтра осадок повышает износ насоса, забивает форсунки опрыскивателей, и ухудшает качество раствора при смене препарата.
Мы рекомендуем использовать такую систему только для растворения жидких препаратов. Для сухих — только если требуются не большая концентрация и небольшой объем готового раствора, и не требуется высокая производительность.
Если вы хотите получить быстрое и качественное растворение любых компонентов, то обязательно нужно использовать миксер предварительного растворения.
Миксер представляет собой бочку с мощной гидромешалкой, объемом обычно 200, 300 или 600 л или больше. На мобильные растворные узлы мы рекомендуем миксеры объёмом 300л и 600л с гидромешалкой гидромониторного типа. На стационарные узлы — либо миксеры 600л (если требуется растворение только жидких препаратов), либо 3500л с двойной системой перемешивания (если применяются сухие препараты в больших объёмах, например за раз требуется растворить сразу биг бег сухого удобрения).
Иногда миксеры делают на базе пластиковых ёмкостей, но чаще — это ёмкости из нержавеющей стали. В миксерах свыше 1м3 обычно недостаточно только гидравлического перемешивания. Мы рекомендуем на объём от 1000л и более устанавливать также рамную механическую мешалку.
Гидромешалки можно применять двух типов – а) гидромониторные, конструктивно – это труба с отверстиями и сетчатым фильтром на входе, удобрения перемешиваются за счет мощного водоворота и прохождения через мелкую ячейку фильтра и б) эжекторные, например, производства компании Arag, такие применяются на опрыскивателях.
2. Какой мощности использовать насос
При модернизации и ремонте растворных узлов, мы встречаем ситуации, когда на ёмкость 11м3 используется насос 40 м3/ч. Мощности насоса в этом случае недостаточно для качественного и быстрого растворения препаратов (особенно сухих). В результате, на приготовление одной порции раствора вместо 30 минут может уйти 3-4 часа. Кроме того, маломощный насос замедляет отгрузку готового раствора.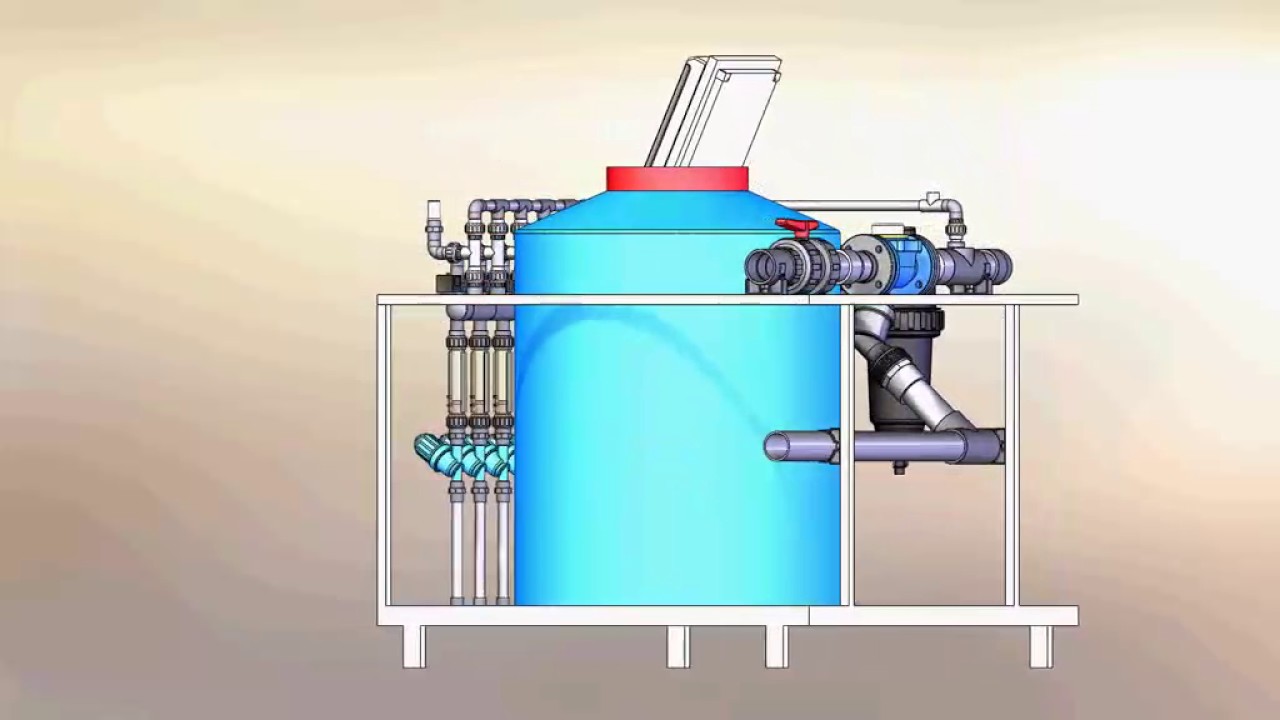
Мы рекомендуем следующие характеристики насосов:
На ёмкость 4-5м3 – 72м3/ч
На ёмкость 5-11м3 – 72-100м3/ч
На ёмкость 30-60м3 – от 100м3 и выше.
Самая простая формула определения необходимой мощности насоса – это разделить объем емкости на производительность насоса в минуту. Мы получим время необходимое на полное перемешивание ёмкости. Например, насос 72 м3/ч (1.2 м3/мин) перемешает ёмкость 11м3 за 10 минут (11/1.2). Оптимальное время для ёмкости 5-10м3 =10 минут, на большие ёмкости (например, жд цистерны 60м3) =30 минут.
3. Эффективная конструкция гидромешалки
Гидроперемешивание должно создавать равномерное движение воды по всей ёмкости для растворения и перемешивания препаратов.
Отсюда распространенные ошибки:
— используется гидравлическая мешалка эжекторного типа с опрыскивателя, но с насосом недостаточной мощности. Мы встречали, когда для эжекторной гидромешалки в растворном узле использовался насос 40м3/ч. В результате удобрения растворялись крайне медленно и было трудно добиться однородности раствора. Мы рекомендуем эжекторную гидромешалку использовать в паре с насосом производительностью от 70м3/ч и более. Например, можно использовать электронасос Auastrong ESST80-65-160/55 (70м3/ч, 2 атм) или мотопомпу Hypro 1543P-130SP, (100 м3/ч, 4 атм)
Мы рекомендуем эжекторную гидромешалку использовать в паре с насосом производительностью от 70м3/ч и более. Например, можно использовать электронасос Auastrong ESST80-65-160/55 (70м3/ч, 2 атм) или мотопомпу Hypro 1543P-130SP, (100 м3/ч, 4 атм)
— слишком большой объем подачи сухого вещества. Сухие препараты засыпаются сразу большим объёмом (н-р, биг-бег) и труднорастворимым комом лежат в ёмкости. Мы рекомендуем обустраивать постепенную подачу сухих препаратов (например, шнековым транспортёром). При больших объемах (биг-бег) рекомендуем всё-таки использовать миксеры предварительного перемешивания с механической и гидравлической системами.
— трубопровод создающий движение воды внутри ёмкости расположен только в одной части бочки. В результате, удобрение растворяется медленно, а раствор получается неоднородным. Мы рекомендуем распределять подающий трубопровод по всей ёмкости. Н-р, можно использовать химостойкий мягкий рукав 3”, расположенный по всей длине ёмкости, с отверстиями по всей длине через определённые расстояния. Такая конструкция отлично работает при гидроперемешивании жидких препаратов или концентрированных маточных растворов. Для сухих мы рекомендуем распределить вход и выход жидкости так, чтобы создать максимальное движение воды. Например, в своих миксерах из нержавеющей стали мы обустраиваем подачу воду напором по касательной на дне миксера, чтобы растворять и приподнимать сухие частицы, при этом одновременно в противоположном направлении работает механическая лопастная мешалка – расположенная по всей длине ёмкости.
Такая конструкция отлично работает при гидроперемешивании жидких препаратов или концентрированных маточных растворов. Для сухих мы рекомендуем распределить вход и выход жидкости так, чтобы создать максимальное движение воды. Например, в своих миксерах из нержавеющей стали мы обустраиваем подачу воду напором по касательной на дне миксера, чтобы растворять и приподнимать сухие частицы, при этом одновременно в противоположном направлении работает механическая лопастная мешалка – расположенная по всей длине ёмкости.
4. Пропускная способность трубопроводов и фильтров
Гидравлическая система (трубопроводы, краны, фильтры) должна обеспечивать достаточную производительность. А для этого всасывающие и напорные трубопроводы, краны и фильтры должны быть соответствующих диаметров.
Мы рекомендуем для насоса 70м3ч использовать трубопровод 3” на вход и 2.5” на выход. Если от насоса до источника воды расстояние больше 10м, то на вход труба увеличивается до 3.5” и более.
5.
 Эффективная гидравлическая схема
Эффективная гидравлическая схема
Гидравлическая схема проектируется под технологический процесс, чтобы время работы узла использовалось максимально эффективно.
Например, на наших узлах мы проектируем схему как правило так, чтобы несколько процессов могли выполняться одновременно — 1) подача воды, 2) перемешивание в миксере, 3) гидроперемешивание в одном из накопителей, 4) отгрузка готового раствора
6. С фильтрами или без
Отсутствие фильтров повышает износ насоса и забивает форсунки опрыскивателей.
Мы рекомендуем устанавливать фильтры на заборной магистрали гидромешалки, на выгрузке, на горловине бака и горловине миксера.
Наиболее критично наличие фильтра на выгрузке– чтобы не забивались форсунки опрыскивателей, и на насосе – чтобы продлить срок службы оборудования.
Фильтры мы рекомендуем применять только сетчатые и обязательно пропускной способности соответствующей производительности насоса. Дисковые фильтры– забиваются. Сетчатые фильтра позволяют менять картриджы, применять картриджи с разными степенями очистки, промывать их.
По характеристикам пропускная способность фильтра должна быть равна или превосходить производительность насоса. рекомендуем следующие параметры фильтров: насос до 50м3/ч — фильтр 3 дюйма пропускной способностью 50м3/ч; на насос 72-100 м3/ч – фильтр 4 дюйма 100м3/ч; на насосы выше 100м3/ч рекомендуем устанавливать несколько фильтров параллельно, т.к. фильтры более 100м3/ч в продаже отсутствуют.
7. Система дозирования
Наш опыт показывает, что наиболее замедляет приготовление раствора и повышает риск ошибок ручное дозирование подачи воды.
Мы рекомендуем, даже при сборе максимально простого растворного узла, при объемах накопительных ёмкостей от 10м3 и более, обустраивать автоматическую дозированную подачу воды. При такой системе оператор устанавливает на щите управления нужное количество воды и включает насос. Система автоматически отмеряет нужное количество воды и отключает насос. Это не очень дорого, но существенно ускоряет и облегчает работу оператора.
Также важными системы дозирования являются:
— указатели уровня жидкости в миксере и накопительных ёмкостях. Позволяет зрительно контролировать объем воды в ёмкостях.
Позволяет зрительно контролировать объем воды в ёмкостях.
— система подачи жидких концентратов. Облегчает подачу жидких препаратов. Мы рекомендуем использовать отдельную небольшую ёмкость, в которую удобно заливать жидкие препараты. Из неё препараты насосом закачиваются в миксер. Не лишним будет оборудовать эту ёмкость системой промывки канистр для полного использования всего концентрата и соблюдения санитарно-эпидемиологических норм.
— система автоматической отгрузки с дозатором. Ускоряет и облегает отгрузку. Оператор просто задаёт на пульте количество отгружаемого раствора и запускает насос. Автоматика сама отключает насос при отгрузке заданного количества.
— сильно ускоряет и повышает точность система дозированной подачи жидких препаратов. Представляет собой несколько небольших ёмкостей (по количеству одновременно используемых препаратов) из которых автоматически подаются жидкие компоненты в миксер растворного узла, количество задается на дисплее.
Рекомендуемые нами производители и модели оборудования:
— для дозирования воды в растворный узел рекомендуем использовать счетчик воды ВСХНд-65 импульсный
— для дозирования жидких концентратов и системы дозирования на выгрузку рекомендуем использовать расходомеры Arag
— для зрительного контроля уровня жидкости в ёмкости рекомендуем Уровнемеры «ARAG»шариковые
При подборе расходомеров для дозирования жидких концентратов нужно учитывать вид препаратов. Например, не все расходомеры способны дозировать масляные препараты.
Например, не все расходомеры способны дозировать масляные препараты.
8. Слив остатков и система промывки
При сборке растворного узла и проектировании системы трубопроводов и кранов очень важно предусмотреть систему промывки и слива остатков при смене препаратов и консервации оборудования.
На практике мы встречаем самостоятельно собранные узлы без системы промывки. Это допустимо при использовании одного препарата. Но такие случаи редки – почти всегда растворный узел используется для приготовления растворов различных препаратов.
Мы рекомендуем обустраивать промывку ёмкостей форсунками, которые устанавливаются внутри ёмкости, работают на 360 градусов и омывают все стенки. Например, можно использовать форсунки для промывки бака на 360° Араг (Arag).
Также обязательно нужно устраивать сливные краны в нижних точках ёмкостей или трубопроводов, откуда остатки по правилам должны сливаться в изолированные накопители-испарители. Система полного слива остатков помимо качества раствора обеспечивает ещё защиту оборудования от повреждения при консервации на зимний период.
9. Химстойкие комплектующие
Как показывает наш опыт ремонтов и реконструкции растворных узлов, использование не химостойких комплектующих является одной из причин, влекущих досрочный выход из строя оборудования растворного узла.
Примеры использования не химостойких комплектующих в растворном узле для удобрений, СЗР:
— использование не химостойких насосов (мотопомп) в системе гидроперемешивания или выгрузки удобрений. В результате, насос выходит из строя за 1 сезон;
— применение металлических, не защищённых от коррозии, трубопроводов. В химически агрессивной среде такие трубопроводы быстро коррозируют. Образующаяся ржавчина забивает фильтры и форсунки;
— применением металлических ёмкостей не защищённых от коррозии. Например, металлических жд цистерн, не защищенных от коррозии; в таких цистернах образуется огромное количество ржавчины, забивающей фильтры, форсунки и ухудшающей качество раствора.
Мы рекомендуем использовать в растворном узле следующие защищенные от коррозии виды оборудования:
— насосы нержавеющие или из химостойкого пластика. Например, Насосы Aquastrong ESST80-65-160/75 (72 м3/ч, 24м) и ESST 100-80-125/75 (114 м3/ч, 12 м) c корпусом из нержавеющей стали; мотопомпы Hypro 1543P-130SP (100 м3/ч), или KEMAGE из химостойкого пластика.
Например, Насосы Aquastrong ESST80-65-160/75 (72 м3/ч, 24м) и ESST 100-80-125/75 (114 м3/ч, 12 м) c корпусом из нержавеющей стали; мотопомпы Hypro 1543P-130SP (100 м3/ч), или KEMAGE из химостойкого пластика.
— ёмкости, специально изготовленные заводом для хранения жидких удобрений. Хорошо себя зарекомендовали за многие годы использования в растворных узлах ёмкости компании Анион, например, для стационарных узлов отлично подходят вертикальные ёмкости с коническим дном объемом 11,5м3 и горизонтальные объёмом 11 м3. На мобильные растворные узлы, требующие повышенной крепости и долговечности иногда используют нержавеющие ёмкости.
— краны нержавеющие больших диаметров и пластиковые фирмы Arag.
— прочие фитинги также должны быть химстойкими.
10. Какие ёмкости использовать
Нередкой ошибкой является использование в мобильном растворном узле ёмкостей, не предназначенных для перевозки жидких удобрений, СЗР, КАС:
А) Использование ёмкостей, не предназначенных для жидких удобрений, СЗР. В результате, ёмкости преждевременно разрушаются от агрессивного воздействия химии.
В результате, ёмкости преждевременно разрушаются от агрессивного воздействия химии.
Б) Использование ёмкостей, не рассчитанных для перевозки тяжелых жидкостей. Н-р, плотность и удельный вес КАС в 1,3 раза больше воды. К ёмкостям для перевозки КАС предъявляются повышенные требования к механической плотности. Ёмкости недостаточной механической прочности при их перевозке (которая в сезон работ очень интенсивна) могут сломаться в дороге или на поле.
Мы рекомендуем использовать только сертифицированные ёмкости специально разработанные и предназначенные заводом для удобрений, СЗР, КАС. В их состав включены добавки, защищающие материал от агрессивных жидкостей. Кроме того, такие ёмкости обладают повышенной механической прочностью, позволяющей перевозить более плотные и тяжелые, по сравнению с водой, жидкости. Также важные характеристики – наличие повышенной защиты от УФ (особенно это важно в южных регионах) и по возможности проверенность временем при использовании для перевозки удобрений.
11. Металлический каркас для мобильных растворных узлов
Мы рекомендуем для мобильного растворного узла использовать металлическую раму, спроектированную для повышенных нагрузок при эксплуатации на полевых и садовых дорогах и для перевозки жидкостей повышенного удельного веса.
Использование удешевленного металлического каркаса, не рассчитанного на высокие нагрузки при интенсивной перевозке, разгрузке – погрузке, и на перевозку тяжелых жидкостей типа КАС (например, 5м3 КАС весят на 1.5 тонны больше, чем тот же объем воды). Это также чревато преждевременной поломкой каркаса при перевозке, погрузке или разгрузке.
Ниже фото металлических каркасов, которые спроектированы для повышенных нагрузок и используются нами для изготовления мобильных растворных узлов.
12. Состав растворного узла для удобрений
Как мы уже писали выше, на практике мы встречаемся с двумя типами растворных узлов:
- растворный узел без миксера
- растворный узел с миксером
12.
 1 Растворный узел без миксера
1 Растворный узел без миксера
Растворный узел без миксера – это бочка, в которой с помощью насоса создается движение воды и этой двигающейся водой растворяются удобрения.
Состав растворного узла без миксера:
- емкость или система ёмкостей, объём подбирается под задачи;
- химостойкий электронасос или мотопомпа;
- система трубопроводов и кранов, обеспечивающая приготовление растворов с помощью гидроперемешивания, а также подачу готового раствора на отгрузку;
- в случае необходимости перемещения — ёмкость, насос и система кранов монтируются на раме.
Многие хозяйства своими руками делают такие растворные узлы, используя емкости 3, 5, 10 м3 и более. По нашему опыту, самостоятельно изготовленные агрегаты часто имеют недостатки:
— плохо растворяют твердые (кристаллические, гранулированные) удобрения. Причины этому а) большой объем воды, в которой происходит перемешивание, б) насос недостаточной мощности и в) неправильная конструкция гидромешалки. Гидромешалка хорошо растворяет удобрения, если вода подается под большим давлением мощным насосом и циркулирует в небольшой емкости. Также важна сама конструкция гидромешалки — трубки, через которую под давлением прогоняется раствор. Гидромешалка может быть гидромониторного или эжекторного типа.
Гидромешалка хорошо растворяет удобрения, если вода подается под большим давлением мощным насосом и циркулирует в небольшой емкости. Также важна сама конструкция гидромешалки — трубки, через которую под давлением прогоняется раствор. Гидромешалка может быть гидромониторного или эжекторного типа.
— низкая производительность. Сухие удобрения очень долго и сложно растворяются простой циркуляцией. Например, сделать 25-30% раствор карбамида с помощью такого «растворного узла» почти нереально или займет необоснованно долгое время.
— такие «растворные узлы» за сезон нередко выходят из строя. Из-за агрессивных жидкостей, которыми являются раствор карбамида, КАС, пестициды – очень быстро портится запорная арматура, выходят из строя обычные, не химостойкие насосы.
Собирая своими руками растворный узел без миксера, встраивайте в него правильную гидромешалку, применяйте химостойкую соединительную арматуру, краны и химостойкий насос. Однако такой РУ не подходит для быстрого приготовления растворов карбамида высокой концентрации и других трудно растворимых сухих удобрений. И во всех случаях он менее производительный, чем растворный узел с миксером.
И во всех случаях он менее производительный, чем растворный узел с миксером.
12.2 Растворный узел с миксером
Более совершенная конструкция, которая может прослужить много сезонов и обеспечит высокую производительность, состоит из основной емкости, миксера, одного или двух химостойких насосов и соединительной/запорной химостойкой арматуры. Принципиально такой узел отличается наличием отдельной емкости – миксера, с мощной гидравлической мешалкой. В больших миксерах (от 1000л и более) гидромешалка дополняется механическим устройством перемешивания.
Итак, пройдемся по основным элементам растворных узлов, конструкция которых отработана нами уже в течение многих лет и показал свою надежность и производительность.
Основная емкость с системой гидроперемешивания. Можно применять пластиковые емкости 2, 4.5 и 11 м3 или нержавеющие емкости 4.5 , 6, 15 м3 и др.объемов. Несколько емкостей могут объединяться — например, РУ объемом 9м3 из двух соединенных емкостей по 4. 5м3, или РУ 22 м3 — 2 емкости по 11м3. При выборе пластиковых емкостей следует учитывать толщину стенок, механическую прочность, защиту от УФ. Мы рекомендуем ёмкости компании — производителя «Анион.» В основной емкости (емкостях) обязательно устанавливается система гидроперемешивания – она необходима для создания однородного раствора необходимой концентрации при поступлении в неё концентрированного раствора из миксера.
5м3, или РУ 22 м3 — 2 емкости по 11м3. При выборе пластиковых емкостей следует учитывать толщину стенок, механическую прочность, защиту от УФ. Мы рекомендуем ёмкости компании — производителя «Анион.» В основной емкости (емкостях) обязательно устанавливается система гидроперемешивания – она необходима для создания однородного раствора необходимой концентрации при поступлении в неё концентрированного раствора из миксера.
Изготавливая растворный узел своими руками выбирайте качественную емкость, чтобы она прослужила Вам много сезонов, не разрушилась преждевременно от солнца, химии и транспортировки.
Миксер. Представляет собой бочку из нержавеющей стали с мощной гидромешалкой, объемом обычно 200, 300 или 600 л. В миксера свыше 600л рекомендуем установить рамную механическую мешалку с редуктором. Гидромешалки могут быть двух типов – а) гидромониторные, конструктивно – это труба с отверстиями и сетчатым фильтром на входе, удобрения перемешиваются за счет мощного водоворота и прохождения через мелкую ячейку фильтра и б) эжекторные, произвоства компании Arag, такие применяются на опрыскивателях.
Компания Агросектор может изготовить для вас миксер любого объема, с гидравлической и /или механической мешалкой.
Насос. Обеспечивает а) работу миксера, б) гидроперемешивание в основной емкости в) заправку опрыскивателя или транспортных цистерн. Насос должен обеспечивать высокое давление, быть высокопроизводительным и стойким к агрессивным жидкостям. Мы для этих целей рекомендуем нержавеющие электронасосы Aquastrong ESST80-65-160/75 (72 м3/ч, 24м) и ESST 100-80-125/75 (114 м3/ч, 12 м) и химостойкие мотопомпы HYPRO1543Р – 130SP (13 л.с, Qmax = 100м3/час, Pmax = 4 атм). В растворных узлах, где не планируется приготовление КАС – для миксера можно использовать насос Сперони (Италия)CS32-200В, он дешевле и на удобрениях (при отсутствии КАС) служит долго.
На мобильных РУ 1-10 м3 обычно достаточно одного насоса, который с помощью системы кранов переключается либо в режим работы миксера, либо перемешивания в основной емкости, либо выгрузки. В стационарных узлах, и по желанию заказчика в мобильных узлах, для увеличения производительности желательно ставить 2 насоса – один на миксер, второй на мешалку в основной емкости и выгрузку.
Фильтры. Большой сетчатый фильтр на заборной магистрали гидромешалки, фильтр сетчатый на выгрузку, фильтры горловины бака и горловины миксера.
Указатели уровня жидкости в миксере и емкостях.
Электрощит — щит управления насосом / насосами.
Арматура запорная и соединительная — система трубопроводов, шаровых кранов, заправочный (выгрузной) рукав и быстроразъемные соединения нержавеющие и из химостойкого пластика.
13. Работа растворного узла — технологический процесс
Для понимания, какие процессы должна обеспечивать конструкция растворного узла опишем работу стационарного растворного узла 23м3 (производства компании Агросектор).
При помощи насосной станции дозированной подачи воды производится заправка миксера и накопительной емкости 11500 л. Оператор устанавливает на щите управления нужное количество, например 2000 л. и включает заправку миксера. После заправки миксера водой включается механическая и гидравлическая мешалки в миксере 3500 л. И загружается удобрение, например 1000 кг, через верхнюю крышку при помощи погрузчика. Если нужно заливать жидкий концентрат, для этого установлен нержавеющий премиксер 100 л., который подключен к насосу миксера. Жидкий концентрат в необходимом объеме выливается из канистр в премиксер, а затем оператор промывает канистру (в премиксере установлена специальная форсунка, при нажатии на которую происходит промывка канистр). Количество сухих и жидких препаратов, загружаемое в миксер рассчитывается технологом хозяйства из расчета на одну накопительную емкость 11500 л.
И загружается удобрение, например 1000 кг, через верхнюю крышку при помощи погрузчика. Если нужно заливать жидкий концентрат, для этого установлен нержавеющий премиксер 100 л., который подключен к насосу миксера. Жидкий концентрат в необходимом объеме выливается из канистр в премиксер, а затем оператор промывает канистру (в премиксере установлена специальная форсунка, при нажатии на которую происходит промывка канистр). Количество сухих и жидких препаратов, загружаемое в миксер рассчитывается технологом хозяйства из расчета на одну накопительную емкость 11500 л.
Во время приготовления маточного раствора в миксере параллельно идет заправка водой одной накопительной емкости. После того как маточный раствор готов, приблизительно 10-15 мин., он перегружается при помощи насоса миксера и системы кранов в накопительную емкость 11500 л. Для того чтобы рабочий раствор был однородный и качественный в емкости 11500 л. предусмотрена система гидроперемешивания. До отгрузки рабочего раствора оператор должен включить на 10-15 мин. гидромешалку. Для второй емкости все операции повторяются.
гидромешалку. Для второй емкости все операции повторяются.
Выгрузка рабочего раствора происходит при помощи насоса выгрузки через сетчатый фильтр очистки, расходомер с автоматикой 2ʺ Arag и заправочную консоль.
На каждой емкости и миксере установлены указатели уровня жидкости.
Для перехода работы с другими препаратами, накопительные емкости оборудованы системой промывки. Для промывки необходимо:
1. Установить на ПУ необходимое количество воды для промывки.
2. Выбрать емкость или миксер, в которой будет осуществляться мойка.
3. Включить пуск «Вода мойка»
На заборных трубопроводах предусмотрены краны для слива остатков. При правильном исполнении технологического процесса, средняя производительность растворного узла 23 мᶾ/ч.
14. Гидравлическая схема растворного узла
Чтобы собрать растворный узел для удобрений своими руками нужно представлять его гидравлическую схему
Гидравлическая схема растворного узла – это схему движения жидкости, расположения соединительной и запорной арматуры.
Для примера размещаем здесь гидравлическую схему стационарного растворного узла 22 м2
Остались вопросы? Нужно спроектировать и/или поставить комплектующие на растворный узел?
Наш специалист свяжется с вами, всё расскажет, подскажет и при необходимости направит вам коммерческое предложение.
Получить коммерческое предложение на растворный узел или комплектующие
15. Список комплектующих, которые вы можете приобрести у нас
Миксеры для растворения удобрений
Миксеры любых объёмов для растворения жидких и сухих удобрений. Подберём объём и конструкцию под ваши задачи. При необходимости укомплектуем насосом и автоматикой.
Химостойкие насосы и мотопомпы
В наличии широкий ассортимент центробежных электрических насосов из нержавеющей стали и химстойких пластиковых мотопомп, предназначенных для перекачки КАС, ЖКУ и других агрессивных жидкостей.
Расходомеры
В наличии различные модели расходомеров (счётчиков расхода жидкости) для КАС, ЖКУ и воды. Подберём нужный вариант под ваши задачи.
Подберём нужный вариант под ваши задачи.
Насосные станции
Готовые насосные станции для обеспечения работы растворного узла: для автоматической (по счётчику) подачи воды, для выгрузки готового раствора, для работы миксера и гидроперемешивания в накопительных ёмкостях.
Краны нержавеющие и пластиковые химстойкие больших диаметров
Полный ассортимент нержавеющих и пластиковых химстойких кранов для обвязки растворных узлов для удобрений.
Фильтры больших диаметров для фильтрации готоворо раствора
Фильтры различной пропускной способности для растворных узлов различной мощности.
Прочая запорная и соединительная арматура, а также электроника
Быстроразъёмные соединения, шланги, муфты, электромагнитные клапана, пульты управления и прочее
Получить бесплатную консультацию и коммерческое предложение
Растворные узлы для СЗР Деметра — точное и быстрое приготовление растворов
Производим установки дозирования
и приготовления растворов с 2005 года
- Потоковое приготовление без накопления в емкости
- Скорость приготовления до 1600 л/мин.
 готового раствора
готового раствора - Удаленное управление и составление рецептов
- Не нужен оператор, раствор готовят водители
- Списание СЗР по данным установки
Все Растворные узлы
сертифицированы
+
Емкости под препараты
+
Сенсорная панель
управления
+
Шкаф управления IP65 +
модуль связи и ГЛОНАСС
+ подключение модема
+ разъем для флеш-накопителя
+
Водяной насос
+
Компрессор пневмоклапанов
+
Краны для слива остатков СЗР
+
Мешалка для порошковых препаратов
+
Датчики уровня
+
Насос-дозатор
+
Пандус для заправки препаратов
Основные характеристики
- Рама: моноблок с антикоррозийной обработкой, без внешнего корпуса // дополнительная рама с тентовым покрытием // жесткий корпус сэндвич
- Смешивание препаратов: параллельное
- Система дозации препаратов: периодическая // пропорциональная
- Способ забора препаратов: инжекция // насос-дозатор
- Система подсчета препаратов: весовая // расходомерная
- Производительность: 20 – 100 м3/ч
- Шкаф управления с ЖК панелью 9,7 дюйма
- Питание от сети 380 В
- Система аварийного питания: бензогенератор и блок АВР в комплекте
Емкости под препараты (посты)
- Количество постов: 2 – ∞ ед
- Доступные объёмы постов: 250 л // 500 л // 1000 л // 1500 л // 2000 л
- Материал накопителей: нержавеющая сталь // полипропилен
- Функции накопителей
- Полное опорожнение
- Датчик уровня 0 – 100 % (отображение в литрах)
- Входной фильтр на горловину (сетка)
- Система промывки емкостей ротационными форсунками
- Сливные краны со шлангами для удаления остатков препаратов
- Дыхательный клапан с газоотводчиком
Модуль растворения порошковых препаратов (миксер)
- Количество: 1 – ∞ ед.

- Состав модуля:
- Мотор 380 В с червячным редуктором
- Вал с импеллером VISCO JET
- Регулятор оборотов мешалки
- Система налива воды в емкость
- Электрическая обвязка
- ПО для управления модулем
Гидравлическая группа
- Материал водяных магистралей: нержавеющая сталь // PVC-U
- Материал химических магистралей: нержавеющая сталь // PVC-U
- Насос подачи воды: производительность растворного узла + 10-20%
- Материал насосной части: химстойкий полимер
- Водяной расходомер: электромагнитный // ультразвуковой
- Блок дозирования: нержавеющая сталь // химстойкий полимер
- Фильтр входной водяной: 500 мк, материал — полимер, многоразовый
- Фильтр готового раствора: 100 мк, материал — полимер, многоразовый
- Вход воды: фланец 2,5 дюйма
- Выход готового раствора: фланец 2,5 дюйма
Пневматическая группа
- Шкаф распределения воздуха
- Воздушный компрессор V-100 л, 380 В
- Пневматические приводы кранов
- Воздушный пистолет для продувки
Дополнительное оборудование и функции
- Мобильный (бочковой) насос для забора препарата из канистр и еврокубов
- Светильники для освещения РУ и периметра
- Светозвуковая индикация аварии
- GSM модуль связи
- Система геопозиционироания ГЛОНАСС
- Автоматическая промывка магистралей
- Энергонезависимое хранилище рецептов и истории приготовлений
- Выгрузка истории приготовлений на USB-носитель
- Формирование и отправка отчетов.
 Функция позволяет получать на фиксированный почтовый адрес данные для списания препаратов
Функция позволяет получать на фиксированный почтовый адрес данные для списания препаратов - Система контроля неисправностей оборудования
- Функция удаленного сервиса программного обеспечения
- Ёмкость моющего средства для промывки накопителей
- Премиксер ручного добавления препарата во время приготовления
- Растариватель канистр с премиксером и функцией перекачивания препарата в пост
Габаритные размеры установки рассчитываются под платформу клиента
Оплата
- Предоплата 30-70% стоимости, обсуждается индивидуально.
- Безналичный расчет с НДС или без НДС.
- Бронирование очереди производства происходит после внесения предоплаты.
Доставка
- Доставка осуществляется по России, в Казахстан и Беларусь.

- Возможен самовывоз со склада.
- Бесплатная погрузка на платформу при самовывозе.
Монтаж
- Монтаж в течение 2-х недель после отгрузки.
- Сопровождение первых приготовлений.
- Бесплатное обучение персонала.
РАССЧИТАЙТЕ СТОИМОСТЬ РАСТВОРНОГО УЗЛА
Укажите основные параметры оборудования и СРАЗУ узнайте его стоимость.
Калькулятор стоимости Растворного узла
Видеопрезентация
Растворных узлов
Деметра
ПОЛУЧИТЕ СПЕЦИАЛЬНЫЕ УСЛОВИЯ
при покупке первого растворного узла ДЕМЕТРА в регионе
Узнать подробнее
Стационарные решения системы размерно-структурированных популяций с нелинейным темпом роста i
( x , t ) ( i =1, …, N ) – плотность популяции i -го вида по отношению к размеру x ∈[0, л i ) в момент времени t ∈[0, T ], где – максимальный размер i -го вида; представляет собой взвешенную общую популяцию 90 005 i 90 006-го вида в момент времени 90 005 t 90 006 с весовой функцией ; функция V i ( x , P ( t )) скорость роста i -го вида в зависимости от размера особи 900 05 x и каждое общее население P ( t ) и, следовательно, нелинейный. F i и G i заданы отображения, соответствующие функциям рождения и старения соответственно.
F i и G i заданы отображения, соответствующие функциям рождения и старения соответственно.
Пример 1.1 [модель взаимодействия видов; ср. [11]
Модель взаимодействия N с видами формулируется следующим образом. Скорость роста V i ( x , P ( t )) должно зависеть от каждой взвешенной общей совокупности. Функции F i и G i даны здесь, b i 9001 0 ( x , P ( t )) — коэффициент рождаемости из и -го вида в зависимости от каждой взвешенной общей популяции,0007 j ( t )) — коэффициент смертности i -го вида, вызванный взаимодействием с j -м видом.
Пример 1.2 [(модель субпопуляции; см. [1])
Рассмотрим модель, в которой популяция разделена на N подклассов. В этой модели л i = л для i = 1, …, N . Скорость роста В i 9Предполагается, что 0010 ( x , | P ( t )|) зависит от общей взвешенной численности населения. Функции F i и G i даны Здесь, b ij 900 10 ( x , | P ( t )|) обозначает коэффициент воспроизводства i -го подкласса из j -го подкласса популяции и m i ( x , | P ( t )|) — коэффициент смертности в зависимости от | P ( т )|.
Скорость роста В i 9Предполагается, что 0010 ( x , | P ( t )|) зависит от общей взвешенной численности населения. Функции F i и G i даны Здесь, b ij 900 10 ( x , | P ( t )|) обозначает коэффициент воспроизводства i -го подкласса из j -го подкласса популяции и m i ( x , | P ( t )|) — коэффициент смертности в зависимости от | P ( т )|.
Мы рассматриваем проблему существования ненулевых стационарных решений общей системы ( 1 ), содержащей как многовидовые модели взаимодействия, так и модели субпопуляций, как указано выше. Показано, что проблема существования сводится к некоторым эквивалентным задачам, таким как (1) существование нулевого собственного значения некоторого нелинейного оператора, (2) существование собственного значения 1 так называемой чистой репродукции N × N матрица, и (3) существование ненулевой неподвижной точки некоторого нелинейного отображения из в себя. В случае N =2 мы устанавливаем существование ненулевого стационарного решения, используя задачу с неподвижной точкой в духе Prüss Citation9 и Webb Citation11.
В случае N =2 мы устанавливаем существование ненулевого стационарного решения, используя задачу с неподвижной точкой в духе Prüss Citation9 и Webb Citation11.
Стационарные решения для моделей отдельных видов обсуждались в Citation4. Свойства устойчивости стационарных решений были исследованы с помощью теории полугрупп Фаркасом и Хагеном. Недавно Борхес и др. Citation3 и Farkas et al. Citation6 изучили проблему существования ненулевых стационарных решений для некоторых моделей структурированной совокупности с помощью задач с нулевыми собственными значениями. Кроме того, Walker Citation10 изучил ненулевые стационарные решения для моделей населения с возрастной и пространственной структурой с помощью задачи с фиксированной точкой.
В разделе 2 представлены наши предположения и предварительные результаты. Некоторые характеристики стационарных решений представлены в разделе 3, а затем мы показываем существование ненулевых стационарных решений для моделей двух видов и/или двух подклассов в разделе 4.
2. Предварительные
Пусть и положить п.в. x ∈( l i , l )}, п.в. x ∈ (0, l )}. оснащен нормой , где для . Далее примем следующие гипотезы:
(V) Для каждого i =1, …, N , и удовлетворяет следующему.
и. Существует такое, что для ; В i ( x , P )=0 для .
ii. Для , x ↦ В i ( x , P )∈ C 900 06 1 ([0, l i )).
iii. Для любого r >0 существует V r >0 такое, что для ( x , P ), , | Р | Н , .

(F) Для каждого i =1, …, N , F i имеет вид: при , где P φ=( P 1 φ, …, P N φ) с и удовлетворяет следующим условиям.
и. Существует неубывающая функция такая, что для x и .
ii. Существует неубывающая функция такая, что для всех x ∈[0, l i ) и .
iii. Существует неубывающая функция такая, что для всех x ∈[0, l i ), P , с | Р | Н , .
Для каждого i =1, …, N , G i имеет следующий вид: для , где P φ=( P 1 φ , …, P N φ) с и удовлетворяет следующим условиям.

и. Существует неубывающая функция такая, что для всех х , , .
ii. Существует неубывающая функция такая, что для всех x ∈[0, l i ), .
iii. Существует неубывающая функция такая, что для всех x ∈[0, l i ), P , причем | Р | Н , .
iv. Существует положительная константа такая, что для всех x ∈[0, l i ), .
Примечание 2.1
Для , положить В i ( x , P ):= В i (0, P ) и для , поставить В i ( x , Р ):=0. Затем V i ( x , P ) расширяется до и V удовлетворяет условию Липшица для , и | Р | Н ≤ r .
Затем V i ( x , P ) расширяется до и V удовлетворяет условию Липшица для , и | Р | Н ≤ r .
Для каждого определим характеристическую кривую через ( x 0 , t 0 )∈[0, l i 900 06 )×[0, T ] уникальным решение следующего дифференциального уравнения: Для ( x 0 , t 0 )∈[ л i , л ]× [0, T ], пусть ϕ i ( t ; t 0 , x 0 ):= x 0 , t ∈[0, T 9 0006]. Позволять . При начальное время определяется неявно соотношением0006 N φ) и . Интегрируя уравнение ( 1) вдоль характеристической кривой, мы приходим к следующему определению решений.
Определение 2.2
называется решением уравнения ( 1 ), если оно удовлетворяет , где .
При предположениях (V), (F) и (G) мы можем показать, что для любого начального значения существует единственное локальное решение уравнения (1) для некоторого T >0. Далее предположим, что существует такое, что для каждого j =1, …, N , Тогда существует единственное глобальное решение уравнения (1), удовлетворяющее Приведенные выше факты доказываются такими же рассуждениями, как и в Citation7. Мы обсудим результаты существования более общих динамических моделей, чем уравнение (1), в другом месте Citation8.
3. Стационарные решения
С учетом определения 2.2 определим стационарные решения следующим образом.
Определение 3.1
Говорят, что функция является стационарным решением уравнения ( 1 ) если удовлетворяет
Определите оператор A from to by [ A φ]( x )=([ A φ] 1 ( x ), …, [ A φ] N ( x )), где для φ∈ D ( A ), где Тогда имеем
Предложение 3.
 2 900 03
2 900 03
и — стационарное решение к уравнению ( 1 ) тогда и только тогда, когда и .
Доказательство
Предположим, что и . Тогда имеем Отсюда следует, что Тогда для п.в. , а для п.в. , Таким образом, удовлетворяет уравнению (2).
И наоборот, предположим, что и является стационарным решением. Для x , x + h ∈[0, l i ) существует s , таких что , . Тогда имеем Изменяя переменную , имеем , а значит, так как , заключаем, что дифференцируема п.в. и , п.в. х . Таким образом, и, кроме того, . Так как , Следовательно, . Следовательно, и .
Замечание 3.3
Полагая P = P φ, оператор A можно записать в виде квазилинейной формы A φ= A 903 18 P φ с A P — линейный оператор для каждого фиксированного . Если мы найдем, для которого оператор A P * имеет нулевое собственное значение, то полагая φ * ∈ D ( A P * ) являются соответствующим собственным компонентом, ненулевым стационарным решением φ построено путем размещения его I -й компонент. Такой подход был недавно использован для аналогичных структурированных моделей популяций одного вида Borges et al. Citation3 и Farkas et al. Цитата6.
Такой подход был недавно использован для аналогичных структурированных моделей популяций одного вида Borges et al. Citation3 и Farkas et al. Цитата6.
Предположим теперь, что и . Тогда имеем Определим , i =1, …, N , Решив дифференциальное уравнение (3), получим Из уравнения (4) следует, что
Верно и обратное, и мы имеем
Предложение 3.4
Пусть . Тогда и тогда и только тогда, когда каждый компонент из удовлетворяет уравнениям ( 5 ) и ( 6 ).
Доказательство
Осталось показать часть if. Пусть выполняются уравнения (5) и (6). Из уравнения (5) следует, что Следовательно, и в силу (G)(ii) и уравнения (7), В силу уравнений (5) и (6), имеем Следовательно, находим, что и из уравнения (7), получаем Это завершает доказательство.
Теперь положим Let be a стационарное решение. Отметив это, поставьте и . Затем из уравнения (6) следует, что теперь мы определим матрицу, имеющую ( i , j )-й элемент, который соответствует чистой скорости воспроизводства i -го вида из j -го вида. Пусть a =( a 1 , …, a N ) T , где T означает транспонирование. Тогда соотношение ( 8) можно записать в виде
Пусть a =( a 1 , …, a N ) T , где T означает транспонирование. Тогда соотношение ( 8) можно записать в виде
Таким образом, мы имеем следующие два предложения.
Предложение 3.5
Если не имеет собственного значения 1 для каждого , то существует только нулевое стационарное решение.
Предложение 3.6
Предположим, что имеет собственное значение 1 для некоторого , а является соответствующим собственным вектором. Тогда , определяемое как , является ненулевым стационарным решением.
Лет Q ( P ) — диагональная матрица, определяемая формулой Определите отображение формулой Предположим, что ( P * , a * ) — фиксированная точка отображения f . Затем мы имеем Put с Тогда показано, что и является стационарным решением уравнения (1). Действительно, а значит, уравнения (5) и (6) выполняются. По предложениям 3.2 и 3.4 является стационарным решением. Обратно, пусть – стационарное решение. Затем поставьте и . Здесь обратите внимание, что по предложению 3.2 и, следовательно, имеет смысл. Легко видеть, что удовлетворяет f ( P * , a * )=( P * , a 903 18*). Таким образом, у нас есть
Действительно, а значит, уравнения (5) и (6) выполняются. По предложениям 3.2 и 3.4 является стационарным решением. Обратно, пусть – стационарное решение. Затем поставьте и . Здесь обратите внимание, что по предложению 3.2 и, следовательно, имеет смысл. Легко видеть, что удовлетворяет f ( P * , a * )=( P * , a 903 18*). Таким образом, у нас есть
Предложение 3.7
Нахождение ненулевого стационарного решения уравнения ( 1 ) эквивалентно нахождению ненулевой неподвижной точки отображения f, определенного уравнением ( 10 ).
4. Существование стационарных решений в двухвидовом случае
В этом разделе мы ограничимся двухвидовым случаем, т. е. N =2 и установить существование ненулевого стационарного решения уравнения (1). Ввиду предложения 3.7 будем искать ненулевую неподвижную точку отображения, определяемого уравнением (10).
Для этого воспользуемся следующей теоремой о неподвижной точке Аманна [Citation2, теорема 12. 3] (см. также [Citation11, Proposition 4.2]).
3] (см. также [Citation11, Proposition 4.2]).
Предложение 4.1
Пусть X — банахово пространство и C — замкнутый выпуклый конус в X. При σ>0 пусть C σ :={x∈C:∥x∥≤σ}, и пусть f:C σ →C таково, что f непрерывно и f(C σ ) имеет компактное замыкание в C. Предположим, что
| а. | f(x)≠λx для всех x∈C σ таких, что ∥x∥=σ и для всех λ>1. | ||||
| б. | Существуют τ∈(0, σ) и x 1 ∈C, x 1 ≠0 такие, что x−f(x)≠λx 1 для всех x∈C σ таких, что ∥x∥=τ и для всех λ>0. | ||||
Тогда существует x 0 ∈{x∈C:τ≤∥x∥≤σ} такое, что f(x 0 )=х 0 .
В случае N =2 матрица для имеет два действительных собственных значения λ 1 ( P ) и λ 2 ( P ) таких, что где и . В самом деле, характеристическое уравнение есть и . Тогда наш результат существования ненулевых стационарных решений уравнения (1) формулируется следующим образом.
В самом деле, характеристическое уравнение есть и . Тогда наш результат существования ненулевых стационарных решений уравнения (1) формулируется следующим образом.
Теорема 4.2
Предположим, что N=2 и что
| i. | λ 2 (0)>1, λ 1 (0)≠1 и (или 9 0257 | ||||
| ii. | существует r>0 таких что λ 2 (P)<1 для всех удовлетворяющих |P| 2 ≥r. Тогда существует ненулевое стационарное решение уравнения ( 1 ). ДоказательствоРассмотрим отображение, определяемое уравнением (10), т.е. для и ), где Q ( P ) – матрица, определяемая уравнением и – матрица, определяемая уравнением (11). Поскольку , , В i (0, P ) непрерывны в P , f ( P , a ) является непрерывным. Чтобы показать, что выполняется условие (a) в предложении 4.1, пусть ( P , a )∈ C σ такое, что |( P , a 9 0006 )| 4 =σ и предположим, что существует λ>1 такое, что f ( P , a )=λ( P , a ). Затем обратите внимание, что a i = 0 тогда и только тогда, когда P i = 0 по уравнению (13). Таким образом, вектор A = ( A 1 , A 2 ) должен быть ненулевым, а отношение (14) подразумевает, что A — это собственное вектор, связанное с λ> 1. Тогда по предположению (ii) имеем | Р | 2 < r . Далее мы покажем, что выполняется гипотеза (b) предложения 4.1. Необходимо рассмотреть следующие два случая: случаи λ 1 (0)<1<λ 2 (0) и 1<λ 1 (0)≤λ 2 (0). Заметим, что если λ 1 (0)<1<λ 2 (0), то 1− T 0 + D 0 <0, а если 1<λ 1 (0)≤λ 2 (0), то 1− T 0 + D 0 9032 1 > 0. По непрерывности можно взять достаточно малое τ∈(0, σ) такое, что если | Р | 2 ≤τ, затем 1− T P + D P <0 и λ 2 ( 90 005 P )>1 выполняется в случае λ 1 (0 )<1<λ 2 (0), и 1− T P + D P >0 и λ 2 ( P )>1 выполняется в случае 1<λ 1 (0)≤λ 2 (0). Сначала рассмотрим случаи λ 1 (0)<1<λ 2 (0) и . В этом случае пусть . Чтобы показать, что выполняется гипотеза (b) предложения 4.1, предположим, что существует λ>0 и ( P , a )∈ C σ такое, что |( P , a )| 4 =τ и ( P , a )− f ( P , a )=λ x 1 . Затем у нас есть где I — единичная матрица. Отсюда имеем Поскольку 1− T P + D P < 0, из уравнений (15) и (16) следует, что и . Но тогда, а это противоречит 1− T P + D P <0. Во-вторых, рассмотрим случаи λ 1 (0)<1<λ 2 (0) и . Предположим, что существует λ>0 и ( P , a )∈ C σ такое, что |( P , a )| 4 =τ и ( P , a )− f ( P , a )=λ x 1 . В-третьих, рассмотрим случай 1<λ 1 (0)≤λ 2 (0). Предположим, что существует λ>0 и ( P , a )∈ C σ такое, что |( P , a )| 4 =τ и ( P , a )− f ( P , a )=λ х 1 . Тогда у нас есть Вспомните, что . Если , то матрица положительно определена, что противоречит уравнению (19). Если , то имеем . В самом деле , а значит, . Тогда уравнение (19) переписывается в виде где Поскольку положительно определено и , уравнение (20) дает противоречие. Следовательно, условие (b) в предложении 4.1 выполняется в любом случае. Таким образом, по предложению 4.1 существует ( P * , a * )∈ C σ такое, что f ( P * , a * )=( P * , a * ) и ( P * , a * )≠(0, 0). Замечание 4.3В случае взаимодействия видов, как в примере 1.1, мы принимаем if i ≠ j . Тогда легко видеть, что (или λ 2 ( P ) соответственно) и (или λ 1 ( P ) соответственно). Пусть и . Тогда предположения (i) и (ii) в теореме 4.2 читаются как , , и при достаточно больших | P |> r . Таким образом, теорема 4.2 совместима с Уэббом [Citation11, теорема 4.1], и, грубо говоря, теорема 4.2 утверждает, что если один из двух видов удовлетворяет условию, что чистый коэффициент воспроизводства больше 1, когда общая численность популяции равна нулю, и меньше 1, когда общая численность населения достаточно велика, то существует ненулевое стационарное решение. временные ряды. Нестационарные решения для стационарных уравнений ARMA спросил Изменено Просмотрено $\begingroup$ Под «стационарным» я подразумеваю «слабо стационарный». 9t$, которое оказывается нестационарным решением «стационарного» уравнения (очевидно, что $\mathbb{E}[Y_t]$ не свободен от $t$, так как $X_t$, очевидно, имеет нулевое среднее). Можно ли каким-то образом нарушить свойство слабой стационарности при более общем стационарном AR($p$) процессе? Или, вообще говоря, верно ли, что любое стационарное уравнение AR (или даже ARMA) с дискретным временем имеет нестационарное решение?
$\endgroup$ 5 $\begingroup$ Терминология, использованная в вопросе, не совсем корректна. Вы смешиваете модель (или уравнения) и решение модели. Не имеет смысла говорить об уравнении (в данном случае о системе стохастических разностных уравнений), стационарном или нестационарном. $\endgroup$ $\begingroup$ 9т]=_{т\к\infty}0$$ Таким образом, ответ на ваш вопрос заключается в том, что ваш процесс $Y_t$ , а не нестационарный. Следовательно, это не служит контрпримером. Дополнительные мысли . | ||||

 готового раствора
готового раствора
 Функция позволяет получать на фиксированный почтовый адрес данные для списания препаратов
Функция позволяет получать на фиксированный почтовый адрес данные для списания препаратов


 Заметим, что справедлива следующая оценка: где фигурирует в предположении (G)(iv). Тогда из предположения (F)(ii) имеем Let с , и пусть . Оценка (12) показывает, что f ( C σ ) ограничено и, следовательно, имеет компактное замыкание в .
Заметим, что справедлива следующая оценка: где фигурирует в предположении (G)(iv). Тогда из предположения (F)(ii) имеем Let с , и пусть . Оценка (12) показывает, что f ( C σ ) ограничено и, следовательно, имеет компактное замыкание в . Из уравнений ( 12)–( 14) имеем Это противоречие и условие (а) в предложении 4.1 выполнено.
Из уравнений ( 12)–( 14) имеем Это противоречие и условие (а) в предложении 4.1 выполнено.
 Тогда имеем Из этих уравнений имеем С 1− T P + D P <0, уравнение (17) подразумевает, что . Тогда a 2 >0 и по уравнению (18) имеем , что является противоречием.
Тогда имеем Из этих уравнений имеем С 1− T P + D P <0, уравнение (17) подразумевает, что . Тогда a 2 >0 и по уравнению (18) имеем , что является противоречием. Это завершает доказательство.
Это завершает доказательство.
 {-p})$ не имеет корней на единичной окружности и все корни действительны. 9t$ является нестационарным решением уравнения $\text{AR}(1)$. Таким образом, вопреки вашей терминологии, это не «стационарное уравнение», и оно не «повреждается» наличием нестационарного решения. Нестационарное решение — это просто нестационарная модель, представляющая собой форму процесса $\text{AR}(1)$, согласующегося с рекурсивными уравнениями. Существуют также нестационарные решения уравнений $\text{AR}(p)$.
{-p})$ не имеет корней на единичной окружности и все корни действительны. 9t$ является нестационарным решением уравнения $\text{AR}(1)$. Таким образом, вопреки вашей терминологии, это не «стационарное уравнение», и оно не «повреждается» наличием нестационарного решения. Нестационарное решение — это просто нестационарная модель, представляющая собой форму процесса $\text{AR}(1)$, согласующегося с рекурсивными уравнениями. Существуют также нестационарные решения уравнений $\text{AR}(p)$.