Расчетное напряжение в арматуре: Пособие к СП 52-102-2004 Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелого бетона

Нормативные и расчетные характеристики арматуры

2.19.Основной прочностной характеристикой
арматуры является нормативное значение
сопротивления растяжениюR_s,n,
равное наименьшему значению физического
или условного предела текучести и
принимаемое в зависимости от класса
арматуры по табл.2.7.

Таблица 2.7

2. 20.Расчетные значения сопротивления
арматуры растяжению для предельных
состояний первой группыR_sопределяют по формуле

                                                                           
(2.2)

где γ_s— коэффициент
надежности по арматуре, принимаемый
равным:

1,1 — для арматуры классов А240, А300, А400;

1,15 — для арматуры классов А500, А600, А800;

1,2 — для арматуры классов А540, А1000, В500,
Вр1200, Вр1500, К1400 и К1500.

Расчетные значения R_sприведены (с округлением)
в табл. 2.8.
При этом значения R_s,nприняты равными наименьшим контролируемым
значениям по соответствующим ГОСТ.

Расчетные значения сопротивления
арматуры растяжению для предельных
состояний второй группы R_s,serпринимают равными соответствующим
нормативным сопротивлениямR_s,n(см. табл.2.7).

2.21.Расчетные значения сопротивления
арматуры сжатиюR_scпринимаются равными расчетным значениям
сопротивления арматуры растяжениюR_s,
но не более 400 МПа, при этом для арматуры
класса В500R_sc= 360 МПа.

Расчетные значения R_scприведены в табл. 2.8.

Таблица 2.8

При расчете конструкции на действие
только постоянных и длительных нагрузок,
когда расчетное сопротивление бетона
сжатию R_bпринимается с
учетом коэффициента γ_b1= 0,9 (см. п.2.8)
расчетное сопротивление арматуры сжатиюR_scдопускается принимать
не более 500 МПа (5100 кгс/см²), при
этом для арматуры класса А600 принимаетсяR_sc= 470 МПа (4800 кгс/см²).

Во всех случаях для арматуры класса
А540 принимается R_sc= 200 МПа
(2030 кгс/см²).

2.22.Расчетное сопротивление растяжению
ненапрягаемой поперечной арматуры
(хомутов и отогнутых стержней)R_swснижают по сравнению сR_sпутем умножения на коэффициент условий
работы γ_s1= 0,8, но принимают
не более 300 МПа.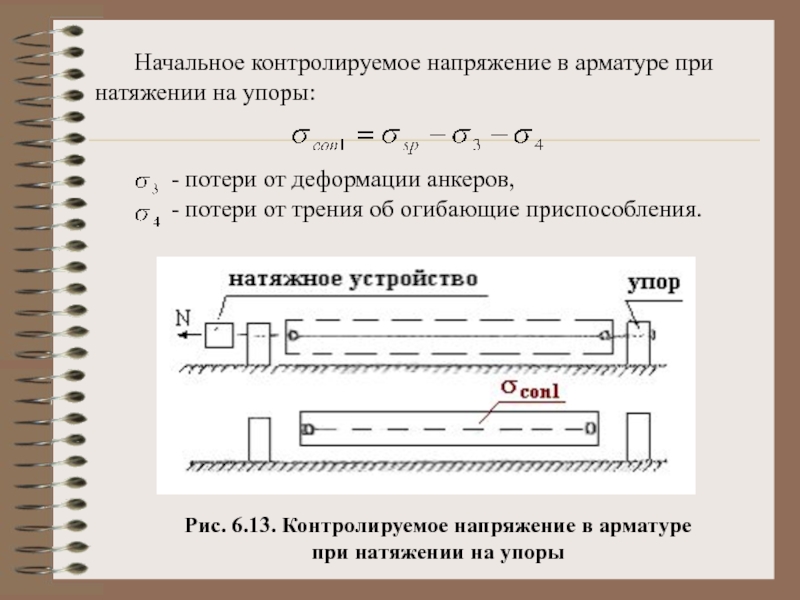 Расчетные значенияR_swприведены (с округлением) в табл.2.9.

Таблица 2.9.

2. 23.При расположении стержней
арматуры классов Вр1200 — Вр1500 попарно
вплотную без зазоров расчетное
сопротивление растяжениюR_sумножается на коэффициент условий
работы γ_s2= 0,85.

2.24.Значение модуля упругости
арматуры всех видов, кроме канатной,
принимается равнымE_s=
200000 МПа (2000000 кгс/см²), а для канатной
арматуры классов К1400 и К1500 —E_s= 180000 МПа (1800000 кгс/см²).

Расчет армирования растянутого стержня в дополнительном модуле RF-CONCRETE Members

В данной статье рассматривается способ определения арматуры для балки, нагруженной растягивающей силой, по норме EN-1992-1-1. Цель статьи состоит в том, чтобы определить растягивающую нагрузку на стержневой элемент (без вынужденных деформаций) и определить параметры арматуры бетона согласно строительными правилам и положениям нормы с помощью программы для расчета конструкций RFEM.

Что означает растяжение для бетонного элемента?

Сечение конструктивного элемента нагружено простым растяжением, если силы, действующие на одной стороне сечения, сокращаются в центре тяжести сечения до единственной силы N. Данная нормальная сила N в этом случае перпендикулярна сечению и направлена к стороне, на которую действуют силы. Собственный вес бетона не учитывается и сечение равномерно подвергается растяжению.

Растягивающее напряжение в стали

У стали с восходящей ветвью на диаграмме напряжения-деформации, выражение для области справа от ветви, соответствующей поведению стали при растяжении, основано на характеристических значениях стали, указанных в §3.2. 7 (2) нормы EN 1992-1-1.

Напряжение в арматуре

σs = fyd + k · fyd — fydεuk — fydEs · εs — fydEs

σs	Напряжение в арматуре
fyd	Расчетное значение предела текучести = fyk/γs
k	Соотношение нормативных пределов = ftk/fyk
εuk	Предельный прогиб
Es	Модуль упругости
εs	Деформация в арматуре = εud = 0,9 ⋅ εuk
fyk	Нормативный предел текучести
γs	Частичный коэфф. запаса стали
ftk	Нормативная величина прочности на растяжение
εud	Расчетное значение предельной деформации

Продольная арматура

Обратите внимание: при расчете простого растяжения бетон, работающий на растяжение, не учитывается. При этом полностью уравновешивают растягивающую силу N_Ed . Необходимая площадь сечения арматуры определяется на основе растягивающей силы и действующего напряжения.

A_s = N_Ed / σ_s
A_s … Площадь арматуры
N_Ed … предельная нормальная сила

Применение теории с помощью дополнительного модуля RF-CONCRETE Members

Рассмотрим пример элемента, подверженного простому растяжению, на основе анализа результатов, полученных для продольного армирования. Ниже приведены исходные данные:

• Постоянные нагрузки: N_g = 100 кН
• Переменные нагрузки: N_q = 40 кН
• Квадратное сечение: 20/20 см
• Класс бетона по прочности: C25/30
• Сталь: S 500 A для восходящей ветви
• Диаметр продольной арматуры: ϕl = 12 мм
• Диаметр поперечной арматуры: ϕt = 6 мм
• Защитный слой бетона: 3 см
• Контроль растрескивания не требуется.

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1.2 Материалы

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

Для проверки настроек материала в RF-CONCRETE Members на рисунке 02 показаны материалы, используемые для бетона и арматуры.

• Таблица 1.2 Материалы

• RFEM модель с постоянными и переменными нагрузками

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

Предельное состояние по несущей способности

Расчетная нагрузка в предельном состоянии по несущей способности:

N_Ed = 1,35 ⋅ 100 + 1,5 ⋅ 40 = 195,00 кН

• Отображение определяющих нагрузок

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1. 2 Материалы

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

Действующее напряжение при растяжении

Предельное состояние по несущей способности для долговременной и переходной расчетной ситуации:

f_yd = 500 / 1,15 = 435 МПа

k = 525 / 500 = 1,05 по таблице C.1 нормы EN 1992-1-1

ε_uk = 25 ‰

ε_ud = 0,9 ⋅ 25 = 22,5 ‰

σ_s = 435 + (1,05 ⋅ 435 — 435) / (2,5 — 435 / (200 000)) ⋅ [2,25 — 435 / (200 000)] = 454 МПа

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1. 2 Материалы

• Отображение определяющих нагрузок

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

Требуемая продольная арматура

Продольная арматура для предельного состояния по несущей способности:

A_s = 0,195 / 454 ⋅ 10⁴ = 4,30 см²

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1.2 Материалы

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

продольная арматура

После введения настройки арматурной стали диаметр 12 мм в дополнительном модуле RF-CONCRETE Members, автоматически заданная дополнительным модулем арматура составляет 4 стержня с симметричным распределением в нижней и верхней частях сечения, то есть 2 x 2 HA12, что соответствует следующей площади сечения арматуры:

A_s = 4 ⋅ 1,13 = 4,52 см²

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1. 2 Материалы

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

• Статически определенная балка

Поперечная арматура

Если поперечная арматура будет задана пользователем, RF-CONCRETE Members может автоматически определить отступы в соответствии с нормой и проверить, соответствует ли расположение требованиям.

В нашем случае, при вводе хомутов диаметром 6 мм, программа определит шаг 0,122 м, но также отобразит предупреждение № 155) в столбце «Примечания», которое изображено на рисунке 07.

• Предупреждение о максимально допустимом расстоянии для хомутов

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1. 2 Материалы

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Статически определенная балка

Формула, относящаяся к §9.2.2 (8) нормы EN 1992-1-1, приведена ниже.

S_l,max = 0,75 ⋅ d
S_l,max … максимальный поперечный шаг хомутов
г … полезная высота
d = h — e — ∅t — ∅_l/2
h … Высота сечения
e … Защитный слой бетона

Указанные выше формулы дают следующие результаты:

d = 0,200 — 0,03 — 0,006 — 0,012 / 2 = 0,158 м

S_l,max = 0,75 ⋅ 0,158 = 0,12 м

Поэтому предупреждающее сообщение 155 появляется из -за того, что расстояние между опорами хомутов в поперечном направлении превышает предельное значение, указанное в стандарте. Проблему можно решить, увеличив количество плеч хомутов в настройках арматуры хомутов, как описано в данном FAQ .

Заключение

После предварительного ввода параметров, модуль RF-CONCRETE Members отображает количество арматурных стержней, требуемых в соответствии с заданным расположением, для проверки растягивающей нагрузки по внутренним силам из программы RFEM. В зависимости от появляющихся предупреждающих сообщений, пользователь может изменить арматуру и ее расположение после расчета.

• Статически определенная балка

• RFEM модель с постоянными и переменными нагрузками

• Таблица 1.2 Материалы

• Отображение определяющих нагрузок

• Предоставленные напряжения и деформации, определенные стержнями RF-CONCRETE

• Требуемая арматура, определяемая стержнями RF-CONCRETE

• Предоставленная арматура, определенная стержнями RF-CONCRETE

• Предупреждение о максимально допустимом расстоянии для хомутов

[1]	Roux, J. (2007). Pratique de l’eurocode 2 — Guide d’application. Paris: Groupe Eyrolles.
[2]	Eurocode 2: Design of concrete structures — Part 1-1: General rules and rules for buildings; EN 1992-1-1:2011-01

Прочность арматуры на растяжение — руководство по конструкции

Прочность арматуры на растяжение и прочность бетона на сжатие — это два основных параметра прочности, которые мы учитываем при проектировании конструкций.

Мы используем арматуру там, где бетон подвергается растягивающим напряжениям и когда он недостаточно прочен, чтобы выдерживать нагрузки.

Таким образом, стальная арматура предназначена для того, чтобы элемент конструкции действовал вместе с бетоном. Сталь слаба на сжатие при воздействии вдоль. Составное действие является лучшим способом для этой проблемы.

Приведем типовой вариант напряжения-деформации арматурных стержней.

Какова прочность арматуры на растяжение?

На приведенном выше рисунке показаны типичные варианты отверждения стали под напряжением и деформацией.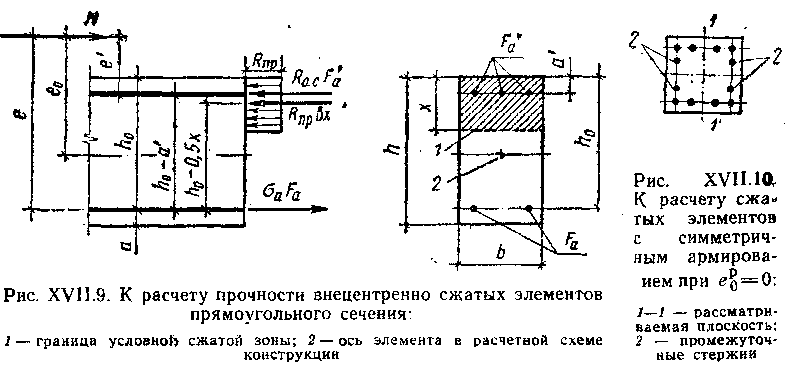

Сначала она прямая, а после некоторого момента (мы назвали ее текучестью) становится нелинейной.

Максимальное напряжение (предельное напряжение), которому подвергается арматурный стержень при удлинении, называется пределом прочности арматурного стержня.

Это пик, после которого начинается образование шейки, а затем напряжение снижается, как показано на рисунке выше. Прочность арматуры на растяжение является очень важным фактором, который нам необходимо знать в нелинейных конструкциях.

В линейном расчете прочность арматуры в основном считается до предела текучести. Однако, когда мы сосредоточились на нелинейных конструкциях, мы максимально использовали напряжение, которое арматурный стержень может оголить без разрушения.

Сейсмостойкие конструкции, расчетные конструкции для взрывных нагрузок, расчеты случайных нагрузок и т. д. в основном занимают нелинейный диапазон арматурной стали.

Изменение прочности арматуры на растяжение

Имеются отклонения в прочности на растяжение или предельной прочности арматурных стержней.

При увеличении прочности арматурного стержня его относительное удлинение уменьшается. Таким образом, для достижения предельного растягивающего напряжения требуется меньшее удлинение (или деформация).

Как показано на рисунке выше, прочность на растяжение увеличивается с увеличением класса арматурной стали. Тем не менее, он показывает меньше напряжения, чтобы достичь отказа.

Как проверить прочность арматуры на растяжение

Во-первых, необходимо выбрать образцы для испытаний. Выборка осуществляется согласно соответствующему своду правил или спецификациям проекта.

В соответствии со стандартом BS 4449:2005 должны быть испытаны три образца для каждого номинального диаметра на каждые 30 тонн.

Для проведения испытаний на растяжение разработаны различные испытательные машины. На следующем рисунке показана типичная испытательная машина.

Как показано на рисунке выше, образец позиционируется, а затем сила будет прикладываться до тех пор, пока он не разрушится.

Теперь давайте посмотрим на типичное соотношение между напряжением и деформацией арматурного стержня, чтобы понять развитие прочности на растяжение.

• При приложении нагрузки к арматуре ее деформация постепенно увеличивается. До точки А напряжение и деформация пропорциональны, и уменьшение и увеличение нагрузки в этом диапазоне не вызывает остаточной деформации стержня.
• Соотношение напряжений и деформаций в этом диапазоне также известно как ваши модули или модуль упругости . (Е = σ/ε).
• Увеличение нагрузки, напряжение достигает точки B, называемой точкой текучести , где начинается текучесть арматуры. Напряжение, при котором начинается текучесть, называется пределом текучести .
• От точки B до точки C дает армирования, что представляет собой увеличение деформации при меньшем изменении деформации, и это пластическая деформация (постоянная) в стержне.
• За пределом текучести материал меняет свою кристаллическую структуру и становится более прочным, устойчивым к деформации. Следовательно, требуется дополнительное напряжение для получения дополнительной пластической деформации за пределами точки C. Это явление известно как деформационное упрочнение . В конце этого процесса нагрузка достигает своего максимального значения.
• Максимальное напряжение (точка D) предел прочности при растяжении он достигает до снижения стресса.
• При растяжении стержня за пределы точки D площадь поперечного сечения стержня уменьшается. Это локализованное уменьшение площади поперечного сечения известно как сужение .
• С уменьшением площади поперечного сечения несущая способность стержня значительно снижается, и в конечном итоге он выходит из строя в точке E. Прочность, при которой арматурный стержень разрушается, известна как прочность на разрыв .
• Кроме того, на приведенной выше кривой есть предсказание, как показано пунктирной линией с уменьшением площади поперечного сечения. Таким образом, фактическое напряжение/истинное напряжение будет выше указанного.

Это процесс, связанный с испытанием арматуры. Как обсуждалось выше, максимальное напряжение, которое может выдержать стержень, известно как предел прочности при растяжении.

Требования к проектным нормам

В соответствии со стандартом BS 4449: 2005 предел прочности на растяжение арматурных стержней отсутствует. Однако в таких стандартах, как ASTM, указано минимальное значение, основанное на марке стали.

В следующей таблице, взятой из технического документа, указаны эти значения.

Для получения дополнительной информации об испытаниях арматуры можно обратиться к статье Испытание арматуры .

Напряжение в арматурной стали в зависимости от ее деформации

Для нормальной конструкции можно сделать одно из следующих предположений (см. рисунок 3.8):

а) наклонная верхняя ветвь с пределом деформации 9где k  = ( f _t / f _y ) _k ,

б) горизонтальная верхняя ветвь без необходимости проверки предела деформации.

где:

f _yk

— нормативный предел текучести арматурной стали, см. § 3.2.2 (3)P.

γ _S

— частный коэффициент для арматурной стали, см. § 2.4.2.4 (1).

k

— пластичность, см. таблицу C.1

ε _uk

— характеристическая деформация арматурной стали при максимальной нагрузке, см. таблицу C.1

Э _с

— расчетное значение модуля упругости арматурной стали, см. § 3.2.7 (4).

f _ярдов

расчетный предел текучести арматурной стали, f _ярдов  =  f _yk 9014 8 / γ _S

ε _ud

расчетная деформация арматурной стали при максимальной нагрузке, ε _ud  =  Coef ( ε _ud )⋅ ε _uk , см. § 3.2.7 (2) для значения Коэфф ( ε _ud ).

If ε _s ≤ ε _se (с ε _se = f _yd / E _s ), напряжение в арматурной стали σ _s = E _с ⋅ ε _с .

If ε _se < ε _s ≤ ε _ud , напряжение в арматурной стали σ _s равно: — ε _се )⋅( к ж _yk — f _yk )/( ε _uk — f _yk / E _s ) для наклонного верхнего отвода,

Это приложение вычисляет
напряжение в арматурной стали σ _s
от ваших входов.