Содержание
Пластичность грунта – описание, формула
Пластичность грунта – это физическое свойство связных дисперсных грунтов менять свою форму без разрыва под воздействием внешних нагрузок. После снятия давления форма сохраняется. Характеристика в большинстве своем зависит от влажности.
Пластичность грунта
Что такое пластичность грунта
Определение пластичности грунта
Определение верхнего предела пластичности
Определение нижнего предела пластичности
Метод раскатывания шнура
Метод прессования
Расчет числа пластичности
Практическое значение показателя пластичности грунтов
Другие свойства грунтов, связанные с пластичностью
Показатель текучести
Консистенция
Активность грунта
Пластичность свойственна глинистым и лёссовидным грунтам с мелкими частицами.
Определяется свойство по верхнему и нижнему пределу пластичности. Цифровым выражением показателя является число пластичности.
Что такое пластичность грунта
В любом грунте присутствует влага.
Она бывает:
- Связанной
Молекулы воды связываются с глинистыми минералами, гумусом и другими веществами. Чаще всего такой тип встречается в глинистых и пылеватых грунтах, плодородных почвах, торфе. Связанная влага с трудом удаляется при высушивании. - Капиллярной
Эта вода находится в мелких порах с размерами 0,001-1 мм. Она способна подниматься из нижних горизонтов в верхние под влиянием силы поверхностного натяжения. Жидкость может отжиматься и удаляться из открытых капилляров, из закрытых – только после их разрушения. - Осмотической
Вода проникает в микроагрегаты и глинистые зерна под влиянием осмотических сил. Она связывается с минералами, отвечает за набухание грунта и его пластические свойства.
- Свободной
Вода находится в крупных порах с размерами больше 1 мм. Она не связана с химическими элементами грунта, свободно удаляется под давлением или при высушивании.
Пластические свойства проявляются, когда в материале преобладает капиллярная и осмотическая влаги. Такая вода накапливается в микропорах глинистого грунта и внутри его зерен.
Существует две основные теории, объясняющие механизм возникновения пластичности:
- Коллоидная
В глинистых грунтах всегда присутствуют коллоиды – мелкие твердые частицы, распределенные в жидкости. Они связывают между собой глинистые зерна грунта, при этом не препятствуют их перемещению относительно друг друга. Коллоиды выступают своеобразной смазкой, позволяющей грунту деформироваться без потери связности. - Гидратная
Согласно этой теории, пластичность обеспечивает тонкая прослойка воды между глинистыми частицами. Она связывает между собой элементы грунта, но при этом они могут перемещаться относительно друг друга.
Обе теории дополняют друг друга. Скорее всего пластичность обеспечивается как коллоидами, так и водными прослойками.
При снижении влажности связь между частицами ослабевает, грунт твердеет или начинает распадаться на куски. Повышение влажности ведет к появлению большого количества свободной воды. Глинистый грунт в таком случае переходит в текучее состояние (превращается в эмульсию).
По показателю влажности определяют основные параметры пластичности:
- Нижний предел пластичности (Wp) – влажность, при которой грунт становится твердым или теряет связность
- Верхний предел пластичности (Wl) – влажность, при которой грунт становится текучим (превращается в жидкую эмульсию)
- Число пластичности (Ip) – разница между верхним и нижним пределом (Ip=Wl-Wp)
Именно на числе пластичности основывается классификация глинистых грунтов (ГОСТ 25100-2011 и новый ГОСТ 25100-2020). Она дана в таблице.
| Тип грунта | Число пластичности, lp |
| Супесь | 1-7 |
| Лёгкий суглинок | 7-12 |
| Тяжёлый суглинок | 12-17 |
| Лёгкая глина | 17-27 |
| Тяжёлая глина | Больше 27 |
Пластичность, даже при определенной влажности, есть не у всех грунтов.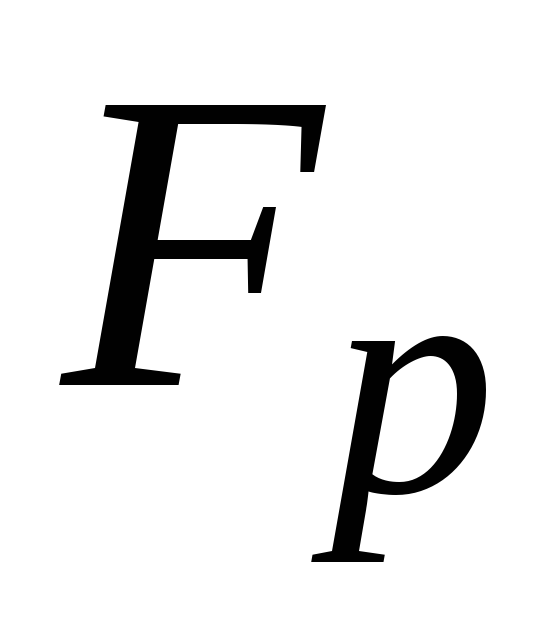
Она зависит от ряда характеристик:
- Гранулометрического состава
Площадь поверхности мелких глинистых частиц очень большая, что позволяет конденсироваться на их поверхности большему количеству воды. - Минерального состава
Глины на основе монтмориллонита (слоистого глинистого минерала, обладающего способностью впитывать большое количество воды и набухать) обладают большей пластичностью, чем на основе каолинита (глинистого минерала класса водных силикатов алюминия с меньшей склонностью к набуханию). - Молекулярного состава
Пластичность падает при возрастании в грунте трехвалентных ионов (алюминия, трехвалентного железа) и увеличивается при появлении одно- и двухвалентных (лития, калия, натрия, двухвалентного железа). - Состава воды
В естественных условиях вода представляет собой раствор солей разной концентрации. Чем больше в ней соли, тем меньше пластичность грунта при определенных параметрах влажности.
Дальше мы опишем, как определяются все показатели пластичности.
Определение пластичности грунта
Верхний и нижний предел пластичности определяют экспериментально по влажности на границе раскатывания и текучести. Затем по полученным данным вычисляют число пластичности. Методики описаны в ГОСТ 5180-2015. Подробно о каждой читайте в соответствующей части статьи.
Определение верхнего предела пластичности
Чтобы определить верхний предел пластичности (или влажность на границе текучести), понадобятся:
- Сушильный шкаф
- Аналитические весы
- Балансирный конус Васильева массой 76±2 г и с углом уклона возле вершины 30°
- Цилиндрическая чаша (идет в наборе с конусом)
- Металлическая или фарфоровая чаша для размельчения грунта диаметром 7-8 см
- Шпатель
- Фарфоровая миска с пестиком
- Терка
- Вазелин
- Сито с ячейками 1 мм
Образец для испытания может иметь нарушенное сложение.
Минеральные грунты берут как с природной влажностью, так и в воздушно-сухом состоянии. Ил и почва должны иметь естественную влажность.
Пробу подготавливают следующим образом:
- Грунт растирают в миске или натирают на терке
- Органические останки с размерами больше 1 мм обязательно вынимают
- Материал просеивают через сито с ячейками 1 мм
- Отбирают пробу массой около 100 г, к ней добавляют дистиллированную воду и выдерживают массу в чаше 2 часа (тяжелые суглинки – 6 часов)
- Лишнюю влагу из ила удаляют фильтровальной бумагой или отжимают образец в хлопчатобумажной ткани
Проведение испытания:
- Подготовленную пасту из грунта выкладывают в цилиндрическую чашу. Она должна полностью заполнить емкость. Поверхность выравнивают на уровне краев чаши.
- Поверхность балансирного конуса смазывают вазелином и подводят его острие к поверхности грунтовой пасты.
- Затем конус плавно опускают, чтобы он погружался в грунт под давлением собственного веса.
- Влажность на границе текучести фиксируется в том случае, когда конус опускается за 5 секунд на глубину 10 мм.
- После этого из образца отбирают пробу 15-30 г и определяют ее влажность по стандартной методике. О ней вы можете прочитать в статье Влажность грунта.
Если за 5 секунд конус погружается на меньшую глубину, чем 10 мм, пасту вынимают из цилиндра, доливают к ней дистиллированную воду, тщательно перемешивают и повторяют опыт.
Если за такой же промежуток времени конус опускается в грунт больше, чем на 10 мм, образец следует просушить. Для этого пасту перекладывают в фарфоровую чашу и слегка просушивают ее на воздухе, постоянно помешивая шпателем.
В США для определения границы текучести используется метод Казагранде (Casagrande). В этом случае в специальную чашу накладывают грунтовую пасту. По центру делают борозду шириной 1,25 см. Затем на приборе с электрическим приводом чашу приподнимают и бросают на резиновое покрытие. На границе текучести после 25 ударов бороздка должна закрыться.
Метод довольно субъективный, поэтому показатели американских, европейских и российских стандартов могут не совпадать.
В Западной Европе, Канаде, Японии, Австралии используется 2 типа цилиндров – весом 80 г и 60 г. В первом случаев угол скоса у вершины 30°, во втором – 60°. В остальном методика не отличается от предложенной российским ГОСТ 5180-2015.
Определение нижнего предела пластичности
Нижний предел пластичности – это влажность, при которой грунт начинает твердеть и распадаться на куски.
Ее определяют двумя методами:
- Раскатыванием шнура
- Прессованием
Их описание вы найдете в продолжении текста.
Метод раскатывания шнура
Для проведения опыта понадобятся:
- Сушильный шкаф
- Аналитические весы
- Стеклянные или металлические бюксы (небольшие баночки с крышками)
- Шпатель
- Ступка с пестиком
- Фарфоровая чаша
- Мелкая терка
- Сито с ячейками 1 мм
- Пластиковая или стеклянная пластина
Проба готовится так же, как и при определении влажности на границе текучести.
Чаще всего из предыдущего образца берут пробу 40-50 г.
Порядок проведения исследования следующий:
- Берут небольшую часть грунта, разминают его и раскатывают на пластине шнур. Его диаметр – 3 мм, длина – около ширины ладони.
- После раскатывания грунт сминают в комок и опять раскатывают. Процедуру повторяют до тех пор, пока шнур не начнет распадаться на куски по 3-10 мм.
- Куски собирают в бюксы и закрывают крышками.
- Когда масса кусочков грунта достигнет 10-15 г, определяют их влажность по стандартной методике.
Метод прессования
Для определения нижнего предела пластичности в этой методике используется прессование грунта в контакте с целлюлозой (фильтровальной бумагой). Суть опыта в том, что под прессом из грунта отжимается жидкость, пока не будет достигнута влажность на границе раската.
Для проведения опыта понадобятся:
- Сушильный шкаф
- Аналитические весы
- Бюксы
- Фарфоровая чаша и ступка с пестиком
- Шпатель
- Сито с ячейками 1 мм
- Фильтровальная бумага
- Хлопчатобумажная ткань
- Деревянные либо металлические пластинки
- Металлический лабораторный шаблон округлой формы толщиной 2 мм и с отверстием по центру (диаметр отверстия 5 см)
- Пресс
Образец готовят таким же образом, как и в предыдущих методиках.
Порядок проведения исследования:
- Шаблон укладывают на хлопчатобумажную ткань. Отверстие заполняют грунтовой пастой и выравнивают ее поверхность на уровне его края.
- Далее шаблон убирают, а оставшийся образец сверху накрывают тканью.
- Затем на грунт снизу и сверху кладут фильтровальную бумагу в ткани.
- Пробу прижимают пластинками и воздействуют на нее прессом, чтобы создать давление 2 МПа (20 кг/см2). Прессуют пробу 10 минут.
- После образец вынимают, снимают с него фильтровальную бумагу и ткань.
- Грунтовую лепешку перегибают пополам. Если на сгибе появилась трещина, значит достигнута влажность на границе раската.
- Если трещина не появилась, берут новую порцию грунтовой пасты и повторяют опыт. Время давления при этом увеличивается на 10 минут.
При использовании метода прессования около 20% образцов нужно параллельно проверять с помощью раскатывания шнура. Результаты обоих способов должны быть сопоставимыми.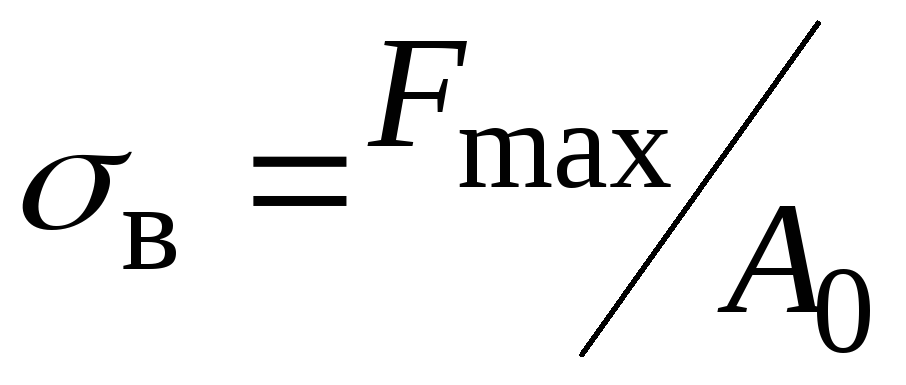
Поскольку методика не является полностью самостоятельной и требует большего количества оборудования, она применяется редко.
Расчет числа пластичности
После определения влажности на границе текучести и раската рассчитывают число, или индекс пластичности (Ip) по формуле:
Число пластичности – это основной показатель, по которому оценивают это свойство. На его основе грунты разделяют на глины, суглинки и супеси. Классификация подана в таблице выше.
На основе числа пластичности также рассчитывают предполагаемую деформацию грунта под нагрузками. Поэтому показатель определяют при планировании строительства на глинистых грунтах.
Практическое значение показателя пластичности грунтов
Пластичность – это один из основных показателей, который позволяет оценивать глинистые грунты.
Он влияет на следующие важные характеристики:
Несущую способность
Пластичная и текучая глина имеет более низкую несущую способность, чем твердая.
Она сильно деформируется под давлением, проседает. Поэтому следует учитывать, при какой влажности грунт перейдет в пластичное состояние. При этом также смотрят, насколько эта влажность выше, чем естественная, на том или ином участке.
- Склонность к набуханию и усадке
По пластичности грунта определяют его активность. Чем выше этот показатель, тем сильнее набухает глинистый грунт. - Структурную прочность
Прочность грунта падает при переходе от твердого к пластичному и от пластичного к текучему состоянию.
Для строительных грунтов высокое число пластичности – отрицательная характеристика. Это значит, что грунт находится в пластичном состоянии при широком диапазоне влажности. Высокий показатель будет полезен в керамической промышленности, при производстве цемента и в ряде других сфер. В них используются пластичные глины, из которых делают посуду, фарфор и другие материалы.
Также отметим, что с пластичностью связано несколько других показателей, которые характеризуют состояние грунтов при разной влажности.
О них вы узнаете дальше.
Другие свойства грунтов, связанные с пластичностью
С пластичностью грунта непосредственно связаны следующие характеристики:
- Показатель текучести
- Консистенция
- Активность грунта
Детальнее об их значении и способах расчета мы расскажем в продолжении этой части статьи.
Показатель текучести
Показатель, или индекс текучести (Il) – это величина, которая рассчитывается по формуле для грунтов с естественной влажностью и нарушенным сложением.
Характеристика помогает предвидеть некоторые механические свойства глинистых грунтов, такие как:
- Влажность, при которой они переходят в текучее состояние
- Степень усадки основания
- Степень деформации под определенным давлением
Индекс текучести рассчитывают по формуле:
В таблице ниже вы найдете классификацию глин, суглинков и супесей в зависимости от показателя текучести. Скажем сразу, что эта типология неофициальная, не закреплена в ГОСТах.
| Тип грунта | Индекс текучести (il) | |||||
| Меньше 0,01 | 0,01 — 0,25 | 0,25 — 0,5 | 0,5 — 0,75 | 0,75 — 1 | Больше 1 | |
| Глины и суглинки | Твёрдые | Полутвёрдые | Тугопластичные | Мягкопластичные | Текучепластичные | Текучие |
| Супеси | Твёрдые | Пластичные | Пластичные | Пластичные | Пластичные | Текучие |
Консистенция
Показатель, или индекс консистенции (Ic) характеризует способность грунта сохранять свою форму и состояние при механическом воздействии и без него. Он включает больше параметров грунта, зависящих от влажности, чем пластичность.
Консистенция бывает жидкой и твердой. Также выделяют ряд переходных форм:
- Текучую
- Текуче-пластичную
- Мягкопластичную
- Тугопластичную
- Пластичную
- Сыпучую
Консистенция определяется в илистых и глинистых грунтах, плодородных почвах.
Она зависит от количества и типа влаги, которая находится в грунте. Наибольшее значение имеют связанная и капиллярная вода. При наличии большого количества свободной влаги грунт переходит в текучее состояние.
У торфа и заторфленных грунтов консистенцию не определяют. Их свойства менять свое состояние зависят не столько от воды и мелких частиц, сколько от природных восков и битумов.
Индекс консистенции определяется по формуле:
В зависимости от показателя, грунты делятся на 4 группы:
- Очень твердые – индекс консистенции больше 1 (литифицированные или окаменевшие глины)
- Твердые – 0,5-1 (сухие глины и суглинки)
- Мягкие – 0,05-0,5 (влажные глинистые грунты)
- Жидкие – меньше 0,05 (водонасыщенные глинистые грунты в текучем состоянии)
Активность грунта
Под активностью глинистого грунта (А) понимают соотношение пластичности и количества глинистых частиц. Показатель дает представление, насколько грунт склонен к набуханию и усадке.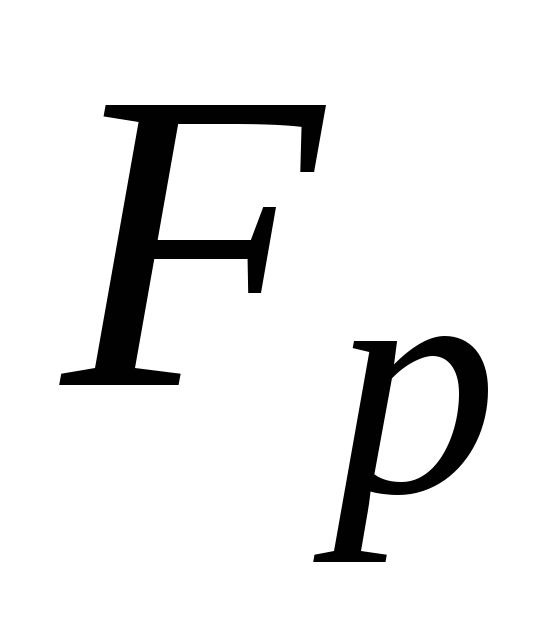
По активности глинистые грунты разделяют на:
- Неактивные глины со слабой склонностью к набуханию (А меньше 0,75)
- Средне активные (А больше 0,75 и меньше 1,25)
- Активные с выраженной склонностью к набуханию (А больше 1,25)
Показатель активности зависит не только от гранулометрического, но и от химического состава.
В таблице даны виды глинистых минералов и показатели их активности (склонности к набуханию).
| Тип минерала | Показатель активности (А) |
| Смектит | 1 — 7 |
| Иллит | 0,5 — 1,0 |
| Каолинит | 0,5 |
| Гидратированный галлуазит | 0,1 |
| Дегидратированный галлуазит | 0,5 |
| Атгапульгит | 0,5 — 1,2 |
| Аллофан | 0,5 — 1,2 |
Вы можете попробовать и самостоятельно определить, какой грунт у вас на участке.
Для этого нужно взять комок грунта и увлажнить его до мягкого состояния. Затем необходимо скатать из него шарик и распластать его в лепешку.
Результаты могут быть следующими:
- Глина распластывается в лепешку без трещин
- Суглинок дает трещины по краям
- Супесь распадается
Но такой метод, разумеется, дает очень условные результаты. Они пригодятся для определения типа грунта на вашем участке, чтобы в последующем можно было улучшить его свойства добавлением песка, перегноя или чернозема. Можно ориентироваться на приблизительные данные и при строительстве небольшого помещения для садового инвентаря. Но если вы планируете возводить жилое здание, строить капитальный гараж или сарай, лучше заказать геодезические исследования у специалистов.
Пластичность и текучесть грунта | СтройFAQ
В зависимости от степени увлажнения глинистые (связные) грунты могут находиться в твердом, пластичном или текучем состоянии.
Переход грунта из одного состояния в другое с изменением влажности обычно происходит скачкообразно и характеризует изменение степени устойчивости грунта под нагрузкой. Поэтому влажность, соответствующая резким переходам грунта и: одного состояния в другое, называется характерной влажностью которая является одной из наиболее важных характеристик грунта.
Пластичность грунта
Пластичностью грунтаназывается его способность деформироваться по действием внешнего давления без разрыва сплошности массы и сохранять приданную форму после прекращения деформирующего усилия.
Для установления способности грунта принимать пластичное состояние определяют влажность, характеризующую границы пластичного состояния грунта текучести и раскатывания.
Граница текучести WL характеризует влажность, при которой грунт из пластичного состояния переходит в полужидкое — текучее. При этой влажности связь между частицами нарушается благодаря наличию свободной воды, вследствие чего частицы грунта легко смещаются и разъединяются.
В результате этого сцепление между частицами становится незначительным и грунт теряет свою устойчивость.
Граница раскатывания WP соответствует влажности, при которой грунт находится на границе перехода из твердого состояния в пластичное. При дальнейшем увеличении влажности (W > WP) грунт становится пластичным и начинает терять свою устойчивость под нагрузкой. Границу текучести и границу раскатывания называют также верхним и нижним пределами пластичности.
Определив влажность на границе текучести и границе раскатывания, вычисляют число пластичности грунта IР.
Число пластичности Ip — разность влажностей, соответствующая двум состояниям грунта: на границе текучести WL и на границе раскатывания Wp. Чем больше число пластичности, тем более пластичен грунт. Минеральный и зерновой составы грунта, форма частиц и содержание глинистых минералов существенно влияют на границы пластичности и число пластичности.
Число пластичности определяется как разность между границей текучести и границей раскатывания грунта: IР = WL — WP
- где WL и Wp определяют по ГОСТ 5180-84.
Деление грунтов по числу пластичности и процентному содержанию песчаных частиц приведено в таблице.
Грунт | Число пластичности Ip | Содержание песчаных частиц (2-0,5мм) |
Супесь | ||
| песчанистая | 1 — 7 | ≥ 50 |
| пылеватая | 1 — 7 | < 50 |
Суглинок | ||
| лёгкий песчанистый | 7 -12 | ≥ 40 |
| лёгкий пылеватый | 7 -12 | < 40 |
| тяжёлый песчанистый | 12- 17 | ≥ 40 |
| тяжёлый пылеватый | 12- 17 | < 40 |
Глина | ||
| лёгкая песчанистая | 17 — 27 | ≥ 40 |
| лёгкая пылеватая | 17 — 27 | < 40 |
| тяжёлая | > 27 | не регламентируется |
Текучесть грунтов
Показать текучести IL выражается в долях единицы и используется для оценки состояния (консистенции) пылевато-глинистых грунтов.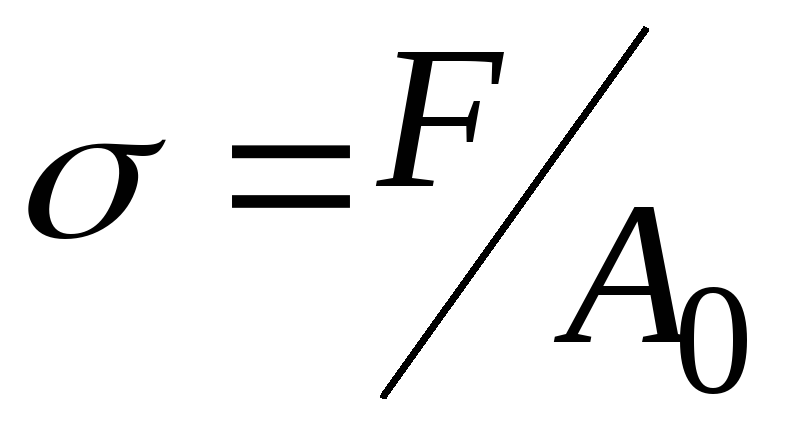
Расчитывается по формуле: IL = (W — Wp) / Iр
- где W — природная (естественная) влажность грунта;
- Wp — влажность на границе пластичности, в долях единицы;
- Ip — число пластичности.
В зависимости от показателя текучести глинистые грунты подразделяются на супеси, суглинки и глины. Показатель текучести для грунтов разной плотности приведены в таблице:
| Консистенция глинистого грунта | Косвенные признаки состояния | Показатель текучести JL |
|---|---|---|
| Супесь | ||
| Твердое | При ударе рассыпается на куски. При растирании пылит, ломается на куски | JL < 0 |
| Пластичное | Легко разминается, сохраняет форму, ощущается влажность, иногда липкость | 0 ≤ JL ≤ 1,00 |
| Текучее | Легко деформируется и растекается при нажатии | JL > 1,00 |
| Суглинок и глина | ||
| Твердое | При ударе распадается на куски, при сжатии в ладони рассыпается, при растирании пылит, тупой конец карандаша вдавливается с трудом | JL < 0 |
| Полутвердое | Ломается без заметного изгиба, поверхность излома — шероховатая, при разминании крошится, тупой конец карандаша оставляет неглубокий след и вдавливается при сильном нажатии | 0 ≤ JL ≤ 0,25 |
| Тугопластичное | Брусок грунта заметно изгибается, не ломаясь.  Кусок грунта разминается струдом. Тупой конец карандаша вдавливается без особого усилия | 0,25 < JL ≤ 0,50 |
| Мягкопластичное | На ощупь влажный, легко разминается, сохраняет приданную форму, но иногда на непродолжительное время, палец вдавливается несколько сантиметров | 0,50 < JL ≤ 0,75 |
| Текучепластичное | На ощупь очень влажный, разминается при легком нажиме, при формировании не сохраняет форму, не раскатывается в жгут т.к. слишком текучий, сильно прилипает | 0,75 < JL ≤ 1,00 |
| Текучее | Стекает по наклонной плоскости толстым слоем (языком), по поведению похож на очень вязкую жидкость | JL > 1,00 |
Грунт
5-05-2021
Сообщить о ошибке (Ctrl+Enter)
12.4 Эластичность и пластичность | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Объяснить предел, при котором деформация материала является упругой
- Опишите диапазон, в котором материалы проявляют пластические свойства
- Анализ упругости и пластичности на диаграмме напряжения-деформации
Константу пропорциональности между напряжением и деформацией мы назвали модулем упругости.
Но почему мы называем это так? Что означает для объекта быть эластичным и как мы описываем его поведение?
Упругость – это тенденция твердых объектов и материалов возвращаться к своей первоначальной форме после устранения внешних сил (нагрузки), вызывающих деформацию. Объект становится эластичным , когда он возвращается к своим первоначальным размерам и форме, когда нагрузка больше не присутствует. Физические причины упругого поведения различаются в зависимости от материала и зависят от микроскопической структуры материала. Например, эластичность полимеров и каучуков обусловлена растяжением полимерных цепей под действием приложенной силы. Напротив, упругость металлов вызвана изменением размера и формы кристаллических ячеек решеток (которые являются материальными структурами металлов) под действием внешних сил.
Двумя параметрами, определяющими эластичность материала, являются его модуль упругости и его предел упругости . Высокий модуль упругости характерен для труднодеформируемых материалов; другими словами, материалы, которые требуют высокой нагрузки для достижения значительной деформации.
Примером может служить стальная лента. Низкий модуль упругости характерен для материалов, легко деформируемых под нагрузкой; например, резинка. Если напряжение под нагрузкой становится слишком высоким, то при снятии нагрузки материал больше не возвращается к своей первоначальной форме и размеру, а принимает другую форму и размер: материал становится необратимо деформированным. предел упругости — это значение напряжения, выше которого материал перестает вести себя упруго, а становится необратимо деформированным.
Наше восприятие эластичного материала зависит как от его предела упругости, так и от его модуля упругости. Например, все каучуки характеризуются низким модулем упругости и высоким пределом упругости; следовательно, их легко растянуть, и растяжение заметно велико. Среди материалов с одинаковыми пределами упругости наиболее эластичным является материал с наименьшим модулем упругости.
Когда нагрузка увеличивается от нуля, результирующее напряжение прямо пропорционально деформации, как показано на (Рисунок), но только тогда, когда напряжение не превышает некоторого предельного значения.
Для значений напряжения в пределах этого линейного предела мы можем описать упругое поведение по аналогии с законом Гука для пружины. Согласно закону Гука степень растяжения пружины под действием приложенной силы прямо пропорциональна величине этой силы. И наоборот, сила реакции пружины на приложенное растяжение прямо пропорционально растяжению. Точно так же деформация материала под нагрузкой прямо пропорциональна нагрузке, и, наоборот, возникающее напряжение прямо пропорционально деформации. Предел линейности (или предел пропорциональности ) — это максимальное значение напряжения, выше которого напряжение больше не пропорционально деформации. За пределом линейности связь между напряжением и деформацией перестает быть линейной. Когда напряжение превышает предел линейности, но все еще находится в пределах предела эластичности, поведение остается упругим, но связь между напряжением и деформацией становится нелинейной.
При напряжениях, превышающих предел упругости, материал демонстрирует пластическое поведение .
Это означает, что материал необратимо деформируется и не возвращается к своей первоначальной форме и размеру даже при снятии нагрузки. Когда напряжение постепенно превышает предел упругости, материал подвергается пластической деформации. Резиноподобные материалы показывают увеличение напряжения с увеличением деформации, что означает, что их становится труднее растянуть, и, в конце концов, они достигают точки излома, где они ломаются. Пластичные материалы, такие как металлы, демонстрируют постепенное снижение напряжения с увеличением деформации, что означает, что они легче деформируются, когда значения напряжения-деформации приближаются к пределу прочности. Микроскопические механизмы, ответственные за пластичность материалов, различны для разных материалов.
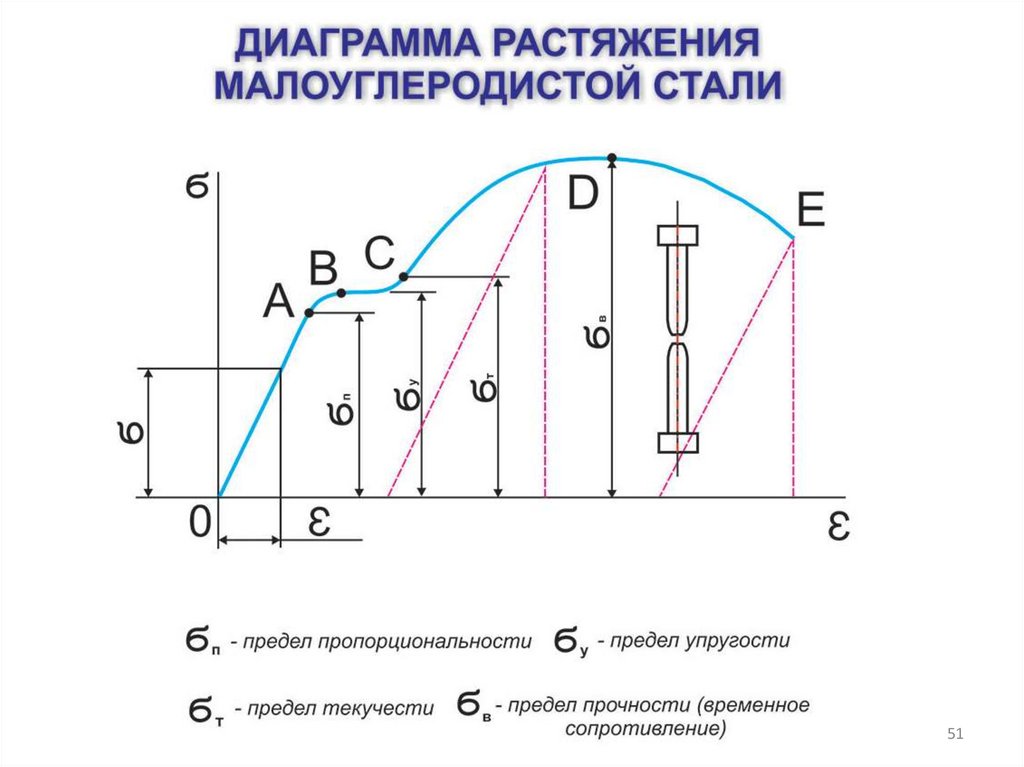
Мы можем изобразить взаимосвязь между напряжением и деформацией на диаграмме напряжения-деформации . Каждый материал имеет свою характеристическую кривую деформации. Типичная диаграмма деформации пластичного металла под нагрузкой представлена на (рис.
). На этом рисунке деформация представляет собой частичное удлинение (не в масштабе). Когда нагрузка постепенно увеличивается, линейное поведение (красная линия), которое начинается в точке без нагрузки (начало координат), заканчивается на пределе линейности в точке H . Для дальнейшего увеличения нагрузки после точки H зависимость напряжение-деформация является нелинейной, но все же упругой. На рисунке эта нелинейная область видна между точками H и E . Все большие нагрузки доводят напряжение до предела упругости E , где упругое поведение заканчивается и начинается пластическая деформация. За пределом эластичности, когда нагрузка снимается, например, в точке P , материал релаксирует, принимая новую форму и размер вдоль зеленой линии. Это означает, что материал постоянно деформируется и не возвращается к своей первоначальной форме и размеру, когда напряжение становится равным нулю.
Материал подвергается пластической деформации при нагрузках, достаточно больших, чтобы вызвать напряжение, превышающее предел эластичности в E .
Материал продолжает пластически деформироваться до тех пор, пока напряжение не достигнет точки разрушения (точки разрыва). За пределами точки разрушения у нас больше нет ни одного образца материала, поэтому диаграмма заканчивается в точке разрушения. Для полноты этого качественного описания следует сказать, что пределы линейности, упругости и пластичности обозначают диапазон значений, а не одну острую точку.
Рисунок 12.25 Типичная диаграмма напряжения-деформации для металла под нагрузкой: График заканчивается в точке разрушения. Стрелки показывают направление изменений при постоянно возрастающей нагрузке. Точки Н и Е — пределы линейности и эластичности соответственно. Между точками H и E поведение нелинейно. Зеленая линия, начинающаяся в точке P, показывает реакцию металла при снятии нагрузки. Остаточная деформация имеет значение деформации в точке, где зеленая линия пересекает горизонтальную ось. 9{4}\,\text{lb}, [/latex], а разрывная нагрузка для стального стержня примерно в девять раз выше.
Резюме
- Предмет или материал является упругим, если он возвращается к своей первоначальной форме и размеру, когда напряжение исчезает. При упругих деформациях со значениями напряжения ниже предела пропорциональности напряжение пропорционально деформации. Когда напряжение выходит за предел пропорциональности, деформация остается упругой, но нелинейной вплоть до предела упругости.
- Объект или материал имеет пластическое поведение, когда напряжение превышает предел упругости. В пластической области объект или материал не возвращается к своим первоначальным размерам или форме после исчезновения напряжения, а приобретает постоянную деформацию. Пластическое поведение заканчивается в точке разрыва.
Ключевые уравнения
«>напряжение и деформация
Концептуальные вопросы
Примечание: Если не указано иное, вес проводов, стержней и других элементов считается незначительным.
{2}\текст{?} [/латекс]
Один конец вертикальной металлической проволоки длиной 2,0 м и диаметром 1,0 мм прикрепляют к потолку, а другой конец прикрепляют к чаше с грузом 5,0 Н, как показано ниже. Положение указателя перед панорамой 4.000 см. Затем к области панорамирования добавляются различные веса, а положение указателя записывается в показанную таблицу. Постройте график зависимости напряжения от деформации для этой проволоки, затем используйте полученную кривую для определения модуля Юнга и предела пропорциональности металла. Какой металл это скорее всего?
| Добавленная загрузка (включая поддон) (Н) | Показание шкалы (см) |
|---|---|
| 0 | 4. 000 |
| 15 | 4.036 |
| 25 | 4,073 |
| 35 | 4.109 |
| 45 | 4.146 |
| 55 | 4.181 |
| 65 | 4.221 |
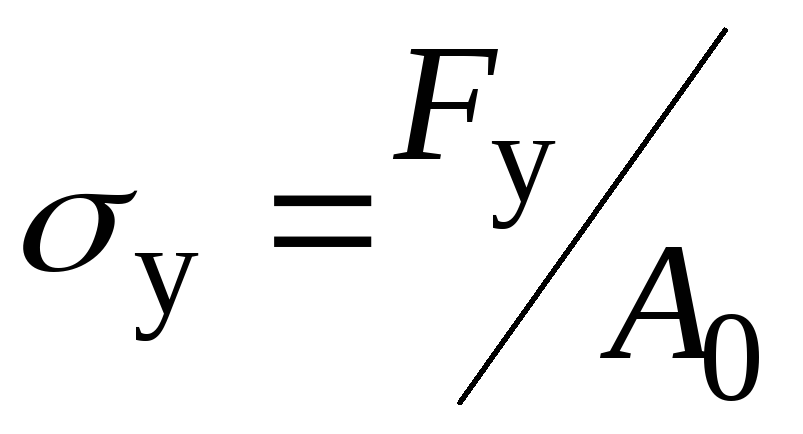
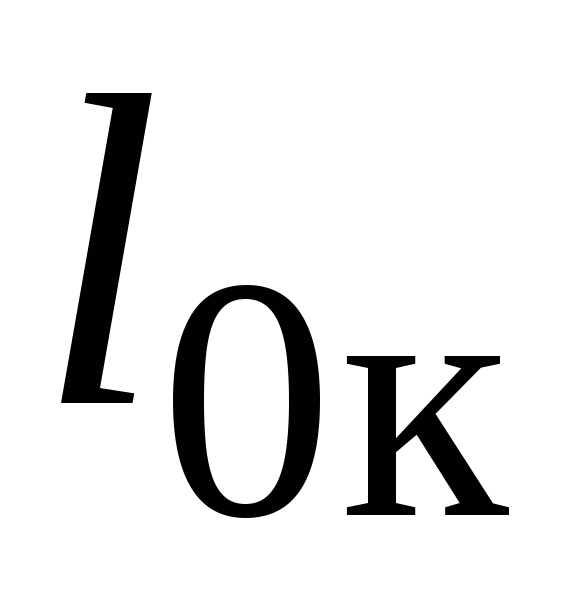
[/latex] Центр масс карандаша расположен 90,0 см от кончика ластика и 11,0 см от кончика грифеля карандаша. Найдите минимальный угол [латекс]\тета[/латекс], при котором карандаш не скользит.
Найдите модуль этой силы, чтобы шар оставался в статическом равновесии. Чему равна сила трения наклона о шар?
Подсказка: На стержень действуют пять сил: два веса колес, две нормальные силы реакции в точках контакта колес с клином и вес стержня.
Если ошейник может скользить без трения по вертикальной направляющей, найти угол [латекс] \ тета [/латекс], при котором стержень находится в статическом равновесии. 9{4}\text{N}, [/latex] под указанными углами. Столб имеет высоту 15,0 м, диаметр 18,0 см и, как считается, имеет вдвое меньшую прочность, чем твердая древесина. а) Рассчитайте сжатие стержня. б) Найдите, насколько он изгибается и в каком направлении. (c) Найдите натяжение растяжки, используемой для удержания столба прямо, если он прикреплен к вершине столба под углом [латекс] 30,0\text{°} [/латекс] к вертикали. Растяжка находится в направлении, противоположном изгибу.
dynasupport.com/tutorial/computational-plasticity/the-equations-for-isotropic-von-mises-plasticity
p, а эквивалентное напряжение принимается равным предел текучести,
При подстановке в уравнение 11 эквивалентное напряжение равно
p и &lamda получается заменой в определении скорости пластической деформации определением эквивалентной скорости пластической деформации