Модуль упругости и модуль деформации: Модули упругости грунтов

Содержание

Модули упругости грунтов — Публикации на официальном сайте Holcim

Эта статья посвящена одному из наиболее важных вопросов современной геотехники. Почему в большинстве случаев определения физико-механических свойств грунта в полевых и лабораторных условиях получаются разные модули деформации при определении их в приборах компрессионного сжатия, трёхосного сжатия, а также в ходе полевых штамповых испытаний? Ответ на этот вопрос в механическом обосновании используемых в настоящее время «моделей» грунта.

Рис. 1

Рис. 2

Ни для кого не секрет, что исторически механика грунтов приняла решение теории деформирования «твёрдого тела», а большинство расчётов основано на модели линейной упругой среды, т.е. модели Гука. В данной модели компоненты напряжения и деформации связаны между собой простыми линейными зависимостями, параметрами которой являются хорошо известные «модули деформации»: это модуль упругости, коэффициент Пуассона, модуль объемного сжатия и модуль сдвиговой (рис. 1). Между этими параметрами постоянно сохраняется пропорциональность выражающиеся через другие модули деформации. Эту информацию можно легко найти в таблицах нормативной документации и учебников по теории упругости (рис. 2) и «традиционно», как в большинстве конструкционных материалов, мы используем для описания деформируемости грунта пару модуль упругости + коэффициент Пуассона.

Однако в связи с тем, что в грунтах ярко выражены пластические деформации и всегда наблюдается нелинейность, принято называть их модулем общей деформации и коэффициентом отно сительного поперечного расширения. Однако в грунтах, как и во всех дисперсных средах, есть некоторая особенность механического поведения. Сопротивление объёмному сжатию и сопротивление сдвигу не линейны и носят обратный характер т.е. пропорциональность между ними не сохраняется в ходе деформирования. Проще говоря, если на начальном этапе модуль объемной деформации низкий, а сопротивление сдвигу высокое, то в конце разрушения наоборот, модуль объемной деформации высокий, а сопротивление сдвигу низкое. В результате соотношения между получаемыми модулями нарушаются и могут применяться только при условии рассмотрения какого-либо отдельного участка деформирования, но не всей диаграммы в целом.

В качестве иллюстрации рассмотрим, как выглядят три наиболее распространённых при требуемых нормативами испытания. Во всех трёх случаях использовалась однородная линейная упругая среда с известными параметрами:

Мд=30 Мпа;

Кп=0,3.

В виртуальной среде модулирования GeoSmart было симулировано нагружение. После оценки результатов с применением методик ГОСТ 12248 и ГОСТ 20276, были получены значения модулей деформации, а там, где это было возможно, коэффициенты Пуассона. Они полностью совпадают что в компрессионных испытаниях, что в трёхосных.

В штамповом испытании, даже в моделируемом упругом теле, была получена другая (хоть и не на много) цифра. Связано это с тем, что формула Шлейхера, которую используют ГОСТ и ОДН на штамповые испытания, не учитывает жесткости более низких слоев или фундамента, если он есть.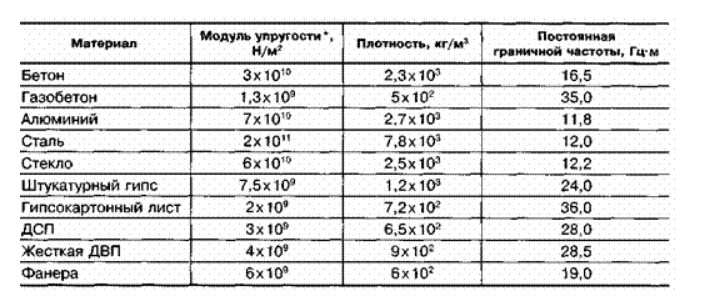 Тем не менее, сходимость результатов есть, и можно сказать, что в условиях идеальной упругой среды всегда были бы хорошие результаты вне зависимости от вида испытаний.

Почему же для грунтовой среды всегда получаются разные модули деформации, на разных приборах приходится использовать разные эмпирические коэффициенты, подобные коэффициенту Магишевой, для перехода от компрессионных и трёхосных испытаний к штамповым? Связано это с так называемой траекторией нагружения, о которой говорилось в начале статьи. Если мы сравним траектории нагружения в различных приборах, в зависимости от типа испытаний, то будет очевидным, что в трехоснике будет преобладать девиаторное нагружение. По традиционной траектории девиаторного раздавливания, СТС, мы увеличиваем в первую очередь девиатор напряжение, но также прирастает и среднее напряжение.

Если же мы будем использовать траекторию ТС, то будем увеличивать исключительно девиатор напряжения, а объемные компоненты будут постоянными.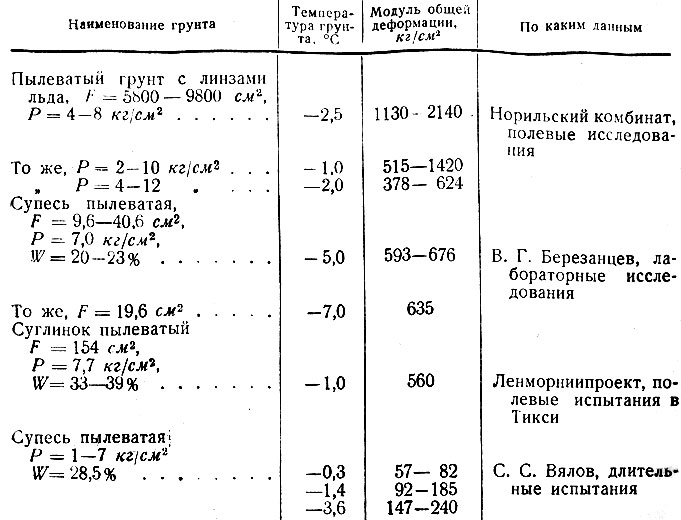

Таким образом, в приборе трёхосного сжатия, в первую очередь определяется жёсткость грунта при сжатии и сдвиге. В приборе компрессионного сжатия траектория нагружения не контролируется, а соотношение между горизонтальным и вертикальным напряжением задаётся коэффициентом бокового давления грунта. Однако совершенно очевидно, что в компрессионном приборе преобладает объемное сжатие и чем выше коэффициент давления, тем ближе расчётное состояние к идеальному гидростатическому обжатию.

Принцип Шлейхера, используемый при штамповых испытаниях на объекте, является линейнодеформируемым полупространством, т.е. напряжение основания во время испытания меняется с глубиной. Именно поэтому штамповые испытания являются наиболее точным определением модулей деформаций из всех доступных. Т.к. по сути мы получаем показатели грунта в виде отклика (отражения) среды на внешнее воздействие, а не наблюдаем отобранный образец в моделируемых условиях. Именно при проведении полевых штамповых испытаний и имея информацию по геологическому разрезу местности можно наиболее точно провести анализ и оценку всех геологических рисков при строительстве.

1.5. Модуль деформации и модуль упругости

Модуль упругости
или начальный модуль упругости бетона

при
сжатии Е_b
соответствует только упругим
деформациям,

возникающим

при
мгновенном загружении.

Связь
между напряжениями и деформациями в
этом случае устанавливается
законом
Гука
_b=E_b_b,
где Е_b
— начальный модуль упругости
бетона;
геометрически он определяется как
тангенс угла наклона
прямой
упругих деформаций (Рис. 1.2.)

E_b
= tg₀

Модуль
полных деформаций Е_b
является величиной переменной.
Геометрически он может быть определён
как тангенс угла наклона касательной
к кривой _b
— _b
в
точке с заданным напряжением

E_b
= tg
=
(1.6.)

Определение
полных деформаций становится
затруднительным в
силу
неопределённости Е_b
.

Для
практических расчётов было предложено
выражать напряжение через полные
деформации с помощью упруго-пластического
модуля Е_b
равного тангенсу угла наклона секущей,
проходящей через начало координат и
точку кривой с заданным напряжением

(1.7)

Выразив
одно и то же напряжение через упругие
и полные деформации, можно получить
связь между модулем упругости

и
модулем
упругопластичности Е_b.

откуда

или

,
(1.8)

_гдекоэффициент
упругопластических деформаций бетона.

По
данным опытов, коэффициент v
меняется
при кратковременном от 1 до 0,45 и до 0,15
при длительном загружении.

При растяжении

(1.9)

где
—
коэффициент,
характеризующий упругопластические
свойства бетона при растяжении,
.

Модуль сдвига
бетона,

(1.10)
где
—
коэффициент
Пуассона. Для бетона
,
при этом

1.6. Арматура

Виды арматуры. По
функциональному назначению арматура
подразделяется на рабочую, конструктивную
и монтажную.

Рабочая
арматура, устанавливаемая по расчёту,
предназначается для восприятия
растягивающих, а иногда и сжимающих
усилий.

Назначение
конструктивной арматуры состоит в
обеспечении цельности
конструкции,
например, конструктивная поперечная
арматура,
увеличивает
сцепление бетона с продольной арматурой,
предохраняет продольные сжатые стержни
от выпучивания, распределяет
действие
сосредоточенных сил на большую площадь,
принимает на себя температурные и
усадочные напряжения.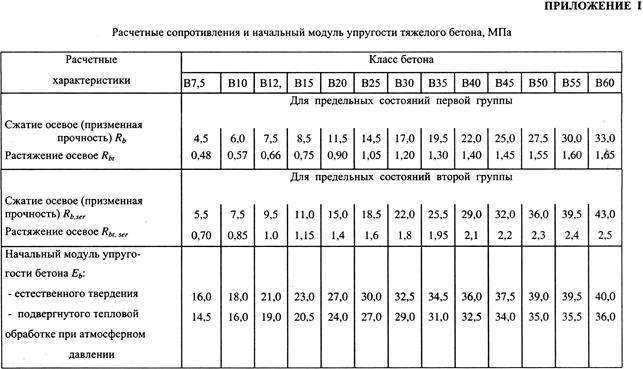

Монтажная
арматура обеспечивает проектное
положение рабочей
арматуры
и служит для создания жёстких каркасов.

По
способу изготовления различают арматуру
стержневую (горячекатаную)
и
проволочную (холоднотянутую).

По форме поверхности
арматуру выпускают гладкой и периодического
профиля.

По
способу применения арматуру делят на
напрягаемую, т.е. подвергаемую
предварительному
напряжению, и ненапрягаемую.

1.6.1. Классификация арматуры

В
зависимости от механических свойств
арматура делится на следующие классы.

Стержневая
арматура:

А)
горячекатаная гладкая класса A—I;
периодического профиля классов

А-П,
А-Ш, A—IV,
A—V,
А-VI.

Б)
термически и
термомеханически упрочнённая
периодического профиля
классов
Ат-Шс,
Ат-IVc,
At—IVk,
At—V,
At—VI.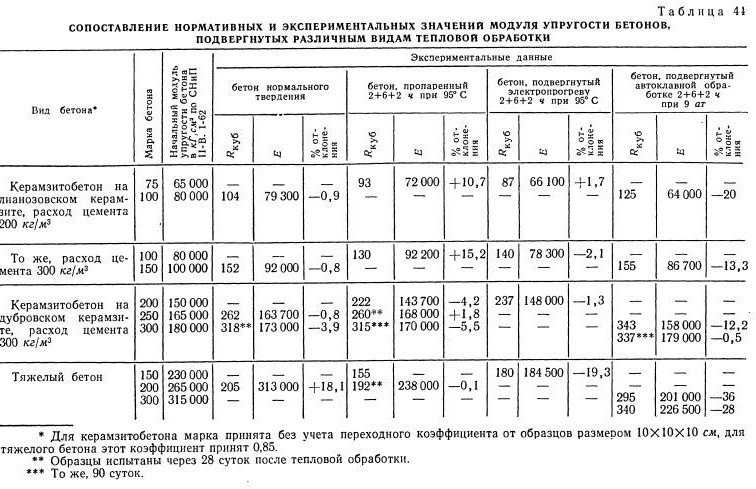

Буква
с указывает на возможность стыкования
сваркой, буква к
—
на повышенную
коррозийную
стойкость.

В)
упрочнённая вытяжкой,
периодического профиля класса А-Шв.

Проволочная
арматура:

г)
арматурная холоднотянутая проволока
обыкновенная гладкая класса B—I
и периодического профиля класса
Вр-
I,
а также высокопрочная гладкая проволока
класса B—II
и периодического
профиля
класса Вр-II.

д)
арматурные канаты семипроволочные
класса К-7
и

девятнадцатипроволочные
класса К-19.

Основные
прочностные и деформативные харарактеристики
арматурных сталей приведены в табл.
прилож. 5.

Класс арматурной
стали выбирают в зависимости от типа
конструкции, наличия предварительного
напряжения и условий

эксплуатации.

В
качестве ненапрягаемой арматуры
железобетонных
конструкций
применяют горячекатаную арматурную
сталь класса А-Ш,

Ат-Шс,
арматурную проволоку класса Вр-I,
а также классов A—I
и А-II,

А-III
в качестве продольной рабочей арматуры,
когда использование других видов
арматуры нецелесообразно. Арматуру
класса А-1
можно применить в качестве монтажной,
а также для хомутов вязаных каркасов и
поперечных стержней сварных каркасов.

В
качестве напрягаемой арматуры
предварительно напряжённых элементов
при длине до 12 м преимущественно применяют
сталь классов

At-IV,
Ат-V,
At-VI.
Допускается
применять арматуру классов В-II
и

Вр-II,
арматуру классов A—IV,
A—V,
А-VI,
арматурные канаты.

При
длине преднапряжённых элементов свыше
12 м преимущественно применяют высокопрочную
арматурную проволоку классов В-II,
Вр-II,
арматурные канаты и горячекатаную
арматурную сталь класса A—V.

В чем разница между модулем упругости и модулем Юнга

8 апреля 2022 г. Автор: Madhu

Ключевое различие между модулем упругости и модулем Юнга заключается в том, что модуль упругости относится к отношению силы, действующей на вещество, к результирующей деформации, тогда как модуль Юнга относится к мере Способность материала выдерживать изменения длины при продольном растяжении или сжатии.

Модуль упругости можно описать как единицу измерения сопротивления объекта или вещества упругой деформации при приложении напряжения. Модуль Юнга можно описать как механическое свойство, которое измеряет жесткость твердого тела при растяжении или сжатии при приложении силы в длину.

СОДЕРЖАНИЕ

1. Обзор и ключевые отличия
2. Что такое модуль упругости
3. Что такое модуль Юнга
4. Модуль упругости и модуль Юнга в табличной форме
5. Резюме – Модуль упругости в сравнении с модулем Юнга

Что такое модуль упругости?

Модуль упругости — единица измерения сопротивления объекта или вещества упругой деформации при приложении напряжения. Он также известен как модуль упругости . Другими словами, модуль упругости представляет собой наклон кривой напряжения-деформации в области упругой деформации. Например. более жесткий материал будет иметь более высокий модуль упругости.

Существует три типа модулей упругости: модуль Юнга, модуль сдвига и объемный модуль. Среди них модуль Юнга имеет тенденцию описывать упругость при растяжении или тенденцию объекта деформироваться вдоль оси, когда вдоль этой конкретной оси действуют противоположные силы. Второй модуль, модуль сдвига, описывает склонность объекта к сдвигу при воздействии на него противоположных сил. Объемный модуль описывает объемную упругость или склонность объекта к деформации при равномерной нагрузке во всех направлениях.

Иногда модуль упругости называют постоянной упругости, тогда как величина, обратная этому параметру, называется модулем упругости. Кроме того, невязкие жидкости специфичны, поскольку они не могут выдерживать напряжения сдвига. Это означает, что модуль сдвига всегда равен нулю.

Что такое модуль Юнга?

Модуль Юнга — это механическое свойство, которое измеряет жесткость твердого тела при растяжении или сжатии при приложении силы в продольном направлении. Он также известен как модуль упругости, потому что это тип модуля упругости. Этот параметр может количественно определять взаимосвязь между напряжением растяжения/сжатия и осевой деформацией в области линейной упругости материала.

Рисунок 01: Наклон относительно модуля Юнга

Модуль Юнга позволяет нам рассчитать изменение размеров стержня, изготовленного из изотропного упругого материала, под действием растягивающих или сжимающих нагрузок. Например, он может измерить, насколько образец материала удлиняется при растяжении или укорачивается при сжатии.

В чем разница между модулем упругости и модулем Юнга?

Ключевое различие между модулем упругости и модулем Юнга заключается в том, что модуль упругости относится к отношению силы, действующей на вещество, к результирующей деформации, тогда как модуль Юнга относится к мере способности материала выдерживать изменения длины, когда он испытывает продольное растяжение или сжатие.

Ниже приведены сводные данные о разнице между модулем упругости и модулем Юнга в табличной форме для параллельного сравнения.

Резюме – Модуль упругости в сравнении с модулем Юнга

Модуль упругости – это единица измерения сопротивления объекта или вещества упругой деформации при приложении нагрузки. Модуль Юнга — это механическое свойство, которое измеряет жесткость твердого тела при растяжении или сжатии, когда сила приложена в продольном направлении. Ключевое различие между модулем упругости и модулем Юнга заключается в том, что модуль упругости относится к отношению силы, действующей на вещество, к результирующей деформации, тогда как модуль Юнга относится к мере способности материала выдерживать изменения длины, когда он при продольном растяжении или сжатии.

Ссылка:

1. «Модуль Юнга». Encyclopædia Britannica , Encyclopædia Britannica, Inc.

Изображение предоставлено:

Описание, пример и факты

Модуль Юнга

См. все СМИ

Связанные темы:: модуль упругости

См. все связанные материалы →

Модуль Юнга , числовая константа, названная в честь английского врача и физика 18-го века Томаса Юнга, которая описывает упругие свойства твердого тела, подвергающегося растяжению или сжатию только в одном направлении, как в случае металлический стержень, который после растяжения или сжатия в продольном направлении возвращается к своей первоначальной длине. Модуль Юнга — это мера способности материала выдерживать изменения длины при продольном растяжении или сжатии. Иногда его называют модулем упругости. Модуль Юнга равен продольному напряжению, деленному на деформацию. Напряжение и деформация могут быть описаны следующим образом в случае металлического стержня под напряжением.

Если металлический стержень с площадью поперечного сечения A тянуть с силой F за каждый конец, стержень растягивается от своей первоначальной длины L ₀ до новой длины L _n . (Одновременно уменьшается поперечное сечение.) Напряжение представляет собой отношение силы растяжения к площади поперечного сечения, или F / A . Деформация или относительная деформация – это изменение длины, L _N — L ₀, разделенная на исходную длину, Ор. (Штамм безразмер.) Таким образом, модуль Янга может быть выражен математически как

Модуль Янга = стресс/ деформация = ( FL ₀)/ A ( L _N — L59.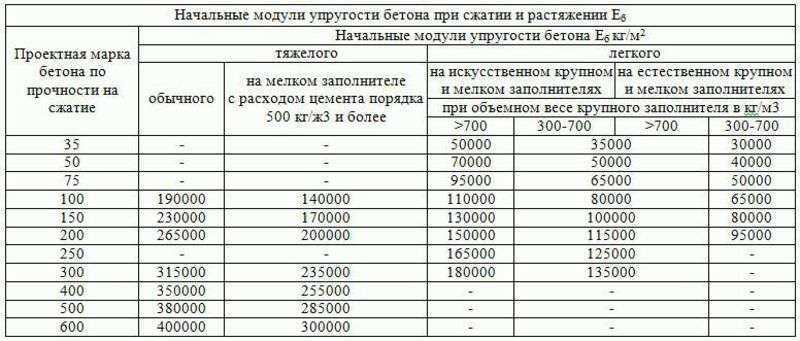 _{_N — L59._{._{_N — L9 _{_N — L9 _N — L _N — _.).}}}}

Это конкретная форма закона упругости Гука. Единицами модуля Юнга в английской системе являются фунты на квадратный дюйм (psi), а в метрической системе — ньютоны на квадратный метр (Н/м ²). Значение модуля Юнга для алюминия составляет около 1,0 × 10 ⁷ фунтов на квадратный дюйм или 7,0 × 10 ¹⁰ Н/м ² . Значение для стали примерно в три раза больше, а это означает, что требуется в три раза больше силы, чтобы растянуть стальной стержень на ту же величину, что и алюминиевый стержень аналогичной формы.

Модуль Юнга имеет смысл только в диапазоне, в котором напряжение пропорционально деформации, и материал возвращается к своим первоначальным размерам при снятии внешней силы. По мере увеличения напряжений материал может либо течь, подвергаясь остаточной деформации, либо окончательно разрушаться.