Содержание
модуль упругости
модуль упругости
иначе модуль Юнга
(англ. elastic modulus)
— коэффициент пропорциональности, связывающий напряжения и деформации в теле.
Описание
Тело, находящееся в состоянии упругого сжатия, растяжения или сдвига, характеризуется тем, что величина его деформации зависит только от величины приложенных к нему напряжений и не зависит от последовательности их приложения. Упругие деформации тела являются обратимыми: при снятии приложенных к нему нагрузок оно возвращается в начальное состояние. В области малых деформаций зависимость величины деформации от нагрузки является линейной функцией (состояние линейной упругости).
В простом случае деформации растяжения удлинение образца в направлении растяжения прямо пропорционально усилию, приложенному к телу. Коэффициент пропорциональности между удлинением образца и усилием, приложенным к нему, поделенный на площадь основания образца, называется модулем Юнга (E) данного материала. Для описания поведения линейно упругого тела также используется коэффициент Пуассона (), который является отношением величины деформации в направлении, перпендикулярном оси растяжения/сжатия, к величине деформации вдоль этой оси при чистом растяжении/сжатии, взятым со знаком минус. Для несжимаемого тела коэффициент Пуассона равен 0,5. Дополнительно применяют следующие коэффициенты: модуль сдвига, или модуль жесткости (G или ), модуль объемного сжатия, или модуль объемной упругости (K), продольный модуль (M). Для полного описания поведения изотропного линейно упругого тела достаточно взять два любых параметра из вышеперечисленных. В общем случае линейной упругости анизотропного тела деформации задаются тензором второго ранга — тензором деформаций, зависимость которого от величин механического напряжения, заданных тензором напряжений, можно определить с помощью тензора упругости — тензора четвертого ранга, содержащего 21 независимый коэффициент.
Для описания поведения линейно упругого тела также используется коэффициент Пуассона (), который является отношением величины деформации в направлении, перпендикулярном оси растяжения/сжатия, к величине деформации вдоль этой оси при чистом растяжении/сжатии, взятым со знаком минус. Для несжимаемого тела коэффициент Пуассона равен 0,5. Дополнительно применяют следующие коэффициенты: модуль сдвига, или модуль жесткости (G или ), модуль объемного сжатия, или модуль объемной упругости (K), продольный модуль (M). Для полного описания поведения изотропного линейно упругого тела достаточно взять два любых параметра из вышеперечисленных. В общем случае линейной упругости анизотропного тела деформации задаются тензором второго ранга — тензором деформаций, зависимость которого от величин механического напряжения, заданных тензором напряжений, можно определить с помощью тензора упругости — тензора четвертого ранга, содержащего 21 независимый коэффициент.
Авторы
- Горячева Ирина Георгиевна
- Шпенёв Алексей Геннадьевич
Источники
- Черных К.
 Ф. Нелинейная упругость // Математическое моделирование систем и процессов. 2001. №9. С. 177–185.
Ф. Нелинейная упругость // Математическое моделирование систем и процессов. 2001. №9. С. 177–185. - Ландау Л. Д., Лифшиц Е.М. Теоретическая физика. Т. VII. Теория упругости — М.: Наука, 1987. — 248 с.
Напишите нам
- А
- Б
- В
- Г
- Д
- Ж
- З
- И
- К
- Л
- М
- Н
- О
- П
- Р
- С
- Т
- У
- Ф
- Х
- Ц
- Ч
- Ш
- Э
- Я
- A
- B
- C
- D
- E
- F
- G
- H
- I
- J
- K
- L
- M
- N
- O
- P
- Q
- R
- S
- T
- U
- V
- W
- X
- Z
Часть 2: получаем данные по материалам для механики конструкций исходя из результатов измерений
В первой части мы обсудили некоторые факторы, которые следует учитывать при преобразовании ваших результатов измерений характеристик материалов в модель состояния. Мы достаточно подробно рассмотрели гиперупругие материалы. Сегодня мы обсудим способы применения нелинейных упругих и упругопластических материалов, а также изучим метод, позволяющий использовать результаты измерений непосредственно в COMSOL Multiphysics.
Мы достаточно подробно рассмотрели гиперупругие материалы. Сегодня мы обсудим способы применения нелинейных упругих и упругопластических материалов, а также изучим метод, позволяющий использовать результаты измерений непосредственно в COMSOL Multiphysics.
Нелинейные упругие материалы
Некоторые материалы проявляют существенную нелинейность уже при малых деформациях. Примерами являются чугун и некоторые керамические материалы. Однако при снятии нагрузки, ведущей к умеренной деформации, они возвращаются в исходное состояние по той же диаграмме деформации, то есть их отклик является упругим. Для описания таких материалов необходима нелинейная упругая модель.
В предыдущей публикации блога мы обсудили гиперупругие материалы. Почему бы не воспользоваться одной из таких моделей, чтобы обеспечить соответствие с диаграммой деформации, построенной на основе результатов измерений, для, например, мелкозернистого чугуна? Проблема в том, что модели гиперупругих материалов рассчитаны на большие деформации. Для эластомеров растяжение может достигать сотен процентов от исходной длины, тогда как область упругих деформаций для металлов и более хрупких материалов составляет обычно менее 1%.
Для эластомеров растяжение может достигать сотен процентов от исходной длины, тогда как область упругих деформаций для металлов и более хрупких материалов составляет обычно менее 1%.
Например, крайне популярная модель Муни — Ривлина является существенно линейной при малых деформациях. Поэтому для нашей задачи она не подходит. В модели Огдена напряжение вычисляется как сумма значений растяжения, возведенных в определенные степени. Однако для малых деформаций растяжение может быть ограничено значениями порядка 0.999 — 1.001. Чтобы модель отражала существенную нелинейность материала, показатель степени в формуле должен быть чрезвычайно большим. Данные измерений вряд ли будут хорошо соответствовать такому закону. Для хрупких материалов более естественной характеристикой деформации является техническая деформация. О различных величинах, используемых для измерения напряжений и деформаций, можно прочитать в публикации «Why All These Stresses and Strains?»
Для решения этой задачи COMSOL предлагает набор нелинейных упругих моделей, рассчитанных на малые деформации. Для работы этих моделей материалов необходим модуль Nonlinear Structural Materials (Нелинейные конструкционные материалы) или Geomechanics (Геомеханика). Эти модели доступны в интерфейсах Solid Mechanics (Механика твердого тела) и Membrane (Мембрана). Рассмотрим способы применения этих материалов.
Для работы этих моделей материалов необходим модуль Nonlinear Structural Materials (Нелинейные конструкционные материалы) или Geomechanics (Геомеханика). Эти модели доступны в интерфейсах Solid Mechanics (Механика твердого тела) и Membrane (Мембрана). Рассмотрим способы применения этих материалов.
Выбор модели нелинейного упругого материала в COMSOL Multiphysics.
Всего доступно девять моделей нелинейных упругих материалов. Некоторые из них представляются в виде простой математической формулы с небольшим количеством параметров. Одна из этих моделей материалов является особенно полезной при обработке экспериментальных данных о зависимости деформации от напряжения: Uniaxial data (Однонаправленные данные). Эта модель предназначена именно для анализа на основе результатов измерений. Рассмотрим настройки этой модели:
Настройки нелинейной упругой модели Однонаправленные данные.
Основная часть данных передается в модель в виде функции, которая описывает зависимость однонаправленной деформации от однонаправленного напряжения. В этом примере результаты измерений представлены в виде функции интерполяции, которая называется
В этом примере результаты измерений представлены в виде функции интерполяции, которая называется stress_strain_curve, однако их можно задать и аналитическим выражением. Функцию интерполяции можно задать в явном виде, как набор результатов измерений, или же выбрать файл, из которого будут считаны эти данные. В нашем примере данные импортируются непосредственно из файла Excel®. Для этого необходим модуль расширения LiveLink™ для Excel®. Однако данные также можно импортировать из текстовых файлов с разделителем-табуляцией.
Импортированная диаграмма зависимости однонаправленной деформации от однонаправленного напряжения.
Однако эта кривая для однонаправленных характеристик не содержит достаточной информации для того, чтобы полностью определить многонаправленный основной закон. Необходимо сделать еще одно предположение. Вам требуется задать либо постоянную величину коэффициента Пуассона, либо модуль объемной упругости. Для многих материалов хорошим приближением является постоянный коэффициент Пуассона в диапазоне от 0,2 до 0,3. Это все, что нужно для построения полной модели материала.
Это все, что нужно для построения полной модели материала.
Обратите внимание на диаграмму деформации выше: кривые для растяжения и сжатия не совпадают. Однако при многонаправленном напряжении определенная точка материала может испытывать натяжение в одном направлении и сжатие в другом. Какую ветвь кривой для материала следует применять в таком случае? Модель материала является изотропной: она обладает одинаковой жесткостью во всех направлениях. Однако определяющей характеристикой является изменение объема. Если локальное изменение объема отрицательно, то применяется ветвь, характеризующая сжатие.
Примечания: теория
Существование изотропного нелинейного упругого материала теоретически возможно только при соблюдении следующих условий:
- Среднее напряжение («давление») или модуль объемной упругости является функцией только объемной деформации.
- Напряжение сдвига или модуль сдвига является функцией только относительной деформации сдвига.
Если эти условия не выполняются, то можно создать нагрузочный цикл, который будет прэнергию, то естьвечный двигатель.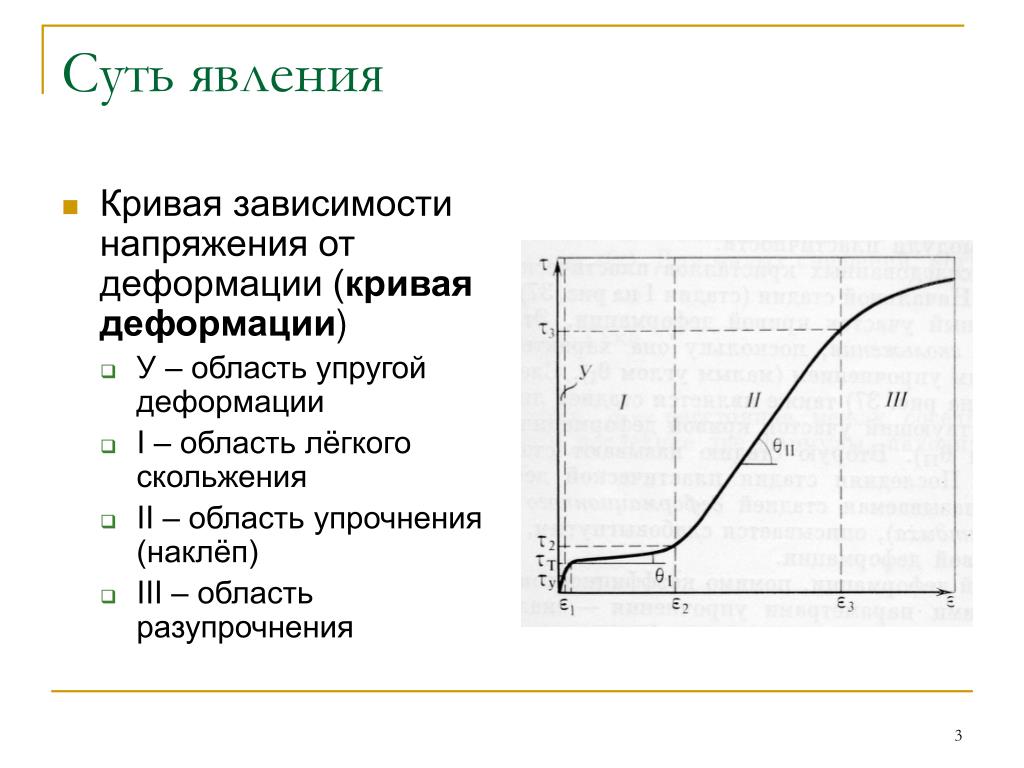
Все встроенные материалы разрабатывались так, чтобы соответствовать этим условиям. Рассмотрим, например, настройки для Двухлинейного упругого материала (Bilinear elastic material). В них вам необходимо указать модули объемной упругости для растяжения и сжатия — не модули Юнга, как можно было ожидать.
Чаще всего специалисты по расчету строительных конструкций имеют дело с модулем Юнга и коэффициентом Пуассона. Это основные характеристики упругого материала. Однако, в соответствии с требованиями выше, если модуль Юнга зависит от деформации, то…
- Функция, описывающая эту зависимость, может принимать только очень специфичные формы.
- Коэффициент Пуассона также должен быть функцией деформации. В результате получается функция, которую очень сложно выразить.
Как тогда можно задать однонаправленные данные при постоянном коэффициенте Пуассона? Для решения этой задачи мы разработали скрытые от пользователя допустимые функции для модуля объемной упругости и модуля поперечной упругости. Модуль Юнга при этом не используется, хотя при взгляде на график этого можно было ожидать.
Модуль Юнга при этом не используется, хотя при взгляде на график этого можно было ожидать.
При этом я видел несколько успешных моделей, в которых аналитик добавил зависимости деформации в модулях Юнга для изотропных или ортотропных материалов в модели упругого материала. Для решения прикладных задач такой метод может подойти. Учебное приложение Modeling Stress-Dependent Elasticity является примером определения зависимого от напряжения модуля Юнга. Чтобы такой подход работал, необходимо, чтобы структура подвергалась преимущественно пропорциональному нагружению (т. е. без поворота направлений главных деформаций).
Консольная балка с различными значениями модуля Юнга для растяжения и сжатия. Свободный конец балки подвергается изгибному моменту. На верхнем графике показано напряжение по Мизесу, на нижнем — текущее значение модуля Юнга.
Когда вы задаете для модели свойство нелинейной упругости при помощи встроенных моделей или собственных выражений, важно сохранять строгое разделение между тангенциальной жесткостью и секущей жесткостью.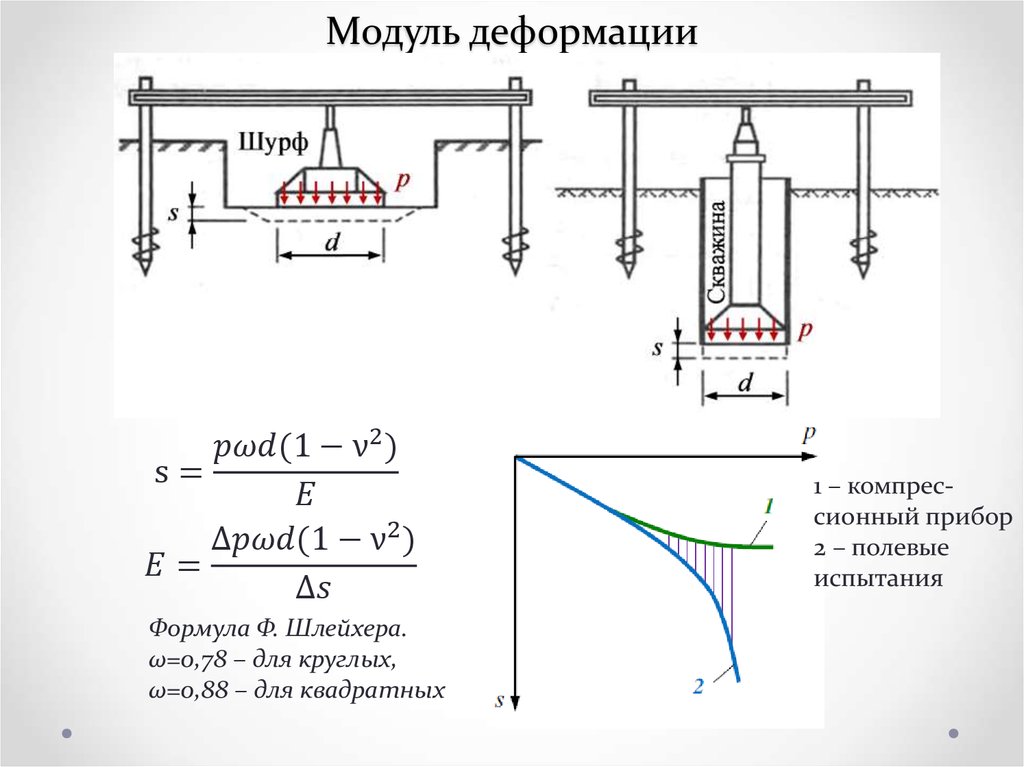 Выражение для нелинейной упругой модели часто похоже на формулу для линейной модели, но с зависимостью коэффициента упругости (который уже не является константой!) от напряжения или деформации. Предположим, что напряжение сдвига \tau связано с деформацией сдвига \gamma как
Выражение для нелинейной упругой модели часто похоже на формулу для линейной модели, но с зависимостью коэффициента упругости (который уже не является константой!) от напряжения или деформации. Предположим, что напряжение сдвига \tau связано с деформацией сдвига \gamma как
\tau = G_S(\gamma) \cdot \gamma
В таком случае модуль сдвига G_S(\gamma) является секущим модулем сдвига. Произведение полной деформации на секущий модуль дает полное напряжение. С другой стороны, тангенциальным модулем сдвига G_T(\gamma) называется жесткость, проявляемая при малых изменениях деформации, как показано на рисунке ниже.
Математическая зависимость между двумя модулями:
G_T(\gamma) = \frac{d \tau}{d \gamma} = G_S(\gamma) + \frac{d G_S(\gamma)}{d \gamma} \gamma
Обычно результаты измерений представляются в форме
\tau = f(\gamma)
Это означает, что секущая жесткость представляется в виде
G_S(\gamma) = \frac{f(\gamma)}{\gamma}
При преобразовании диаграммы деформации в форму секущей с помощью этого выражения необходимо избегать возможного деления на ноль при нулевой деформации.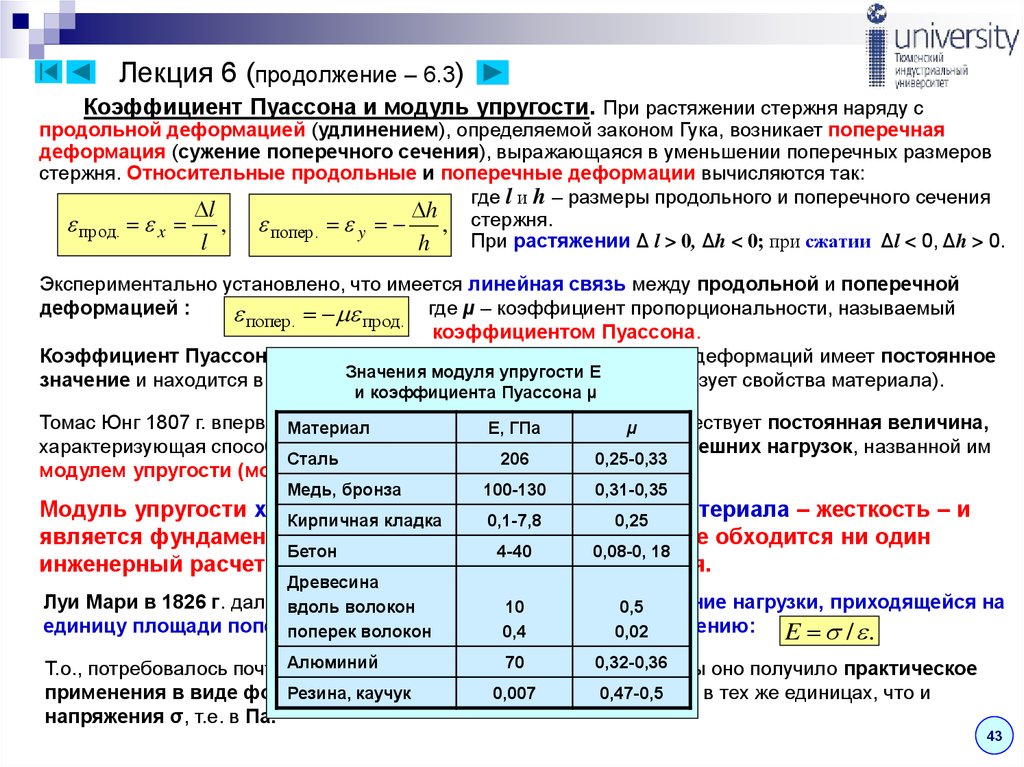 n
n
Модель Степенная зависимость (Power law) в COMSOL Multiphysics основана на первом, более распространенном определении, в котором показатель степени для деформации n связан с наклоном кривой на диаграмме деформации, построенной в полулогарифмических координатах.
Аппроксимация пластичности с помощью нелинейной упругости
Эксперимент на чистое растяжение не позволяет определить, обусловлена ли нелинейность определенных результатов измерений пластичностью. Необходимо также проанализировать кривую разгрузки. Иллюстрацией к этому утверждению служит анимация ниже из предыдущей публикации в блоге.
Применение нелинейной модели упругости для моделирования пластичности рассматривалось в предыдущей публикации в блоге.
Нелинейная модель упругого материала Рамберга— Осгуда, как и модель однонаправленных данных, создавалась в качестве простой замены полной упругопластической модели. Применение нелинейного упругого материала значительно менее требовательно к компьютерным ресурсом. Но каковы ограничения такого подхода?
Но каковы ограничения такого подхода?
- Очевидно, она допускает только непрерывное возрастание нагрузки.
- Если в системе действует несколько внешних нагрузок одновременно, например, сжимающая нагрузка и тепловое расширение, то обычно они не связаны между собой пропорционально. Это может обусловить непропорциональную зависимость локальных напряжений.
- Трехмерные отклики обычно не будут совпадать даже в том случае, если диаграммы однонаправленных деформаций для нелинейной упругой модели и для полной эластопластической модели идентичны. Для пластичности металлов, например, при условии текучести Мизеса, пластическая деформация сохраняет объем. В случае соответствующей нелинейной упругой модели объем не сохраняется.
Заключение
При выборе подходящей модели материала необходимо учитывать общую точность анализа. При решении инженерных задач часто приходится пользоваться неполной информацией: данным о нагрузках, однородности материалов и размерам структуры обычна присуща некоторая неопределенность.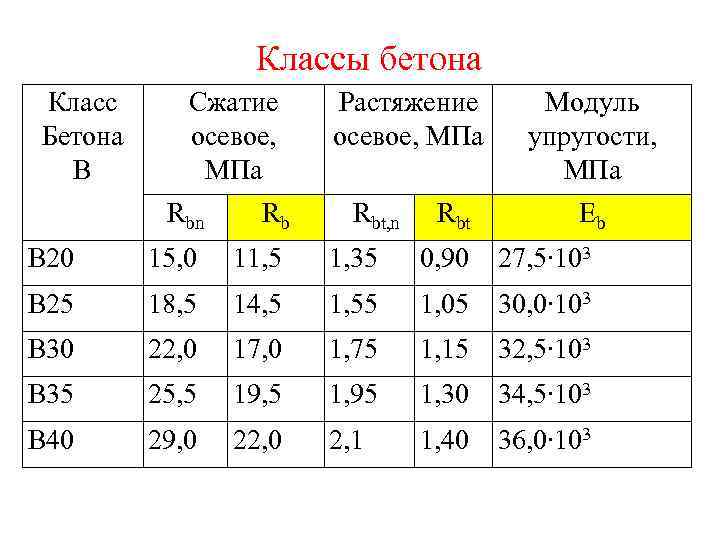 Выбор граничных условий также является аппроксимацией. В этой цепочке качество результатов определяется самым слабым звеном, и таким звеном не всегда является точный математический фундамент модели материала.
Выбор граничных условий также является аппроксимацией. В этой цепочке качество результатов определяется самым слабым звеном, и таким звеном не всегда является точный математический фундамент модели материала.
В предыдущей публикации в блоге я писал, что не стоит просто вводить диаграмму деформаций напрямую.
Почему же сегодня я поступил иначе? Дело в том, что при работе с моделью однонаправленных данных используются фактические результаты измерений. Для всех гиперупругих моделей, а также большей части других нелинейных упругих моделей, под результаты измерений необходимо подогнать математическую модель с малым количеством параметров. Безопасно выполнить такую подгонку возможно только при участии человека.
Что такое модуль упругости?
Рассмотрено
Рагвендра Гопал
|
Последнее обновление: 4 мая 2019 г.
Что означает модуль упругости?
Модуль упругости представляет собой отношение напряжения ниже предела пропорциональности к соответствующей деформации. Это мера жесткости или жесткости материала. С точки зрения кривой напряжение-деформация модуль упругости представляет собой наклон кривой напряжение-деформация в диапазоне линейной пропорциональности напряжения деформации.
Это мера жесткости или жесткости материала. С точки зрения кривой напряжение-деформация модуль упругости представляет собой наклон кривой напряжение-деформация в диапазоне линейной пропорциональности напряжения деформации.
Чем больше модуль, тем жестче материал или тем меньше упругая деформация, возникающая в результате приложения данного напряжения. Модуль является важным расчетным параметром, используемым для расчета упругих прогибов.
Модуль упругости также известен как модуль упругости и иногда упоминается как модуль Юнга.
Модуль упругости может использоваться для измерения сопротивления материалов упругости или деформации; т. е. материал с низкими модулями является гибким и будет сильно растягиваться под давлением. С высокомодульными материалами дело обстоит наоборот, поскольку они очень мало растягиваются при растяжении.
Модуль упругости или просто модуль упругости используется для количественной оценки способности материала сопротивляться непостоянной (упругой) деформации или деформации. При испытании под нагрузкой такие материалы в первую очередь проявляют упругие свойства. Материалы будут растягиваться и возвращаться в прежнее состояние после снятия напряжения. При слишком сильном напряжении материалы будут растягиваться за пределы этой области упругости и предела упругости, чтобы затем войти в область пластичности, где они будут демонстрировать постоянную деформацию.
При испытании под нагрузкой такие материалы в первую очередь проявляют упругие свойства. Материалы будут растягиваться и возвращаться в прежнее состояние после снятия напряжения. При слишком сильном напряжении материалы будут растягиваться за пределы этой области упругости и предела упругости, чтобы затем войти в область пластичности, где они будут демонстрировать постоянную деформацию.
Реклама
Corrosionpedia объясняет модуль упругости
Модуль упругости — это свойство материала, которое описывает жесткость вещества и, следовательно, является одним из наиболее важных свойств твердых материалов. Это отношение напряжения к деформации, когда деформация является полностью упругой. Напряжение определяется как сила на единицу площади, а деформация — как удлинение или сжатие на единицу длины.
Этот модуль можно рассматривать как сопротивление материала упругой деформации. Жесткий материал имеет более высокий модуль упругости. Для большинства типичных металлов величина этого модуля колеблется от 45 гигапаскалей (магний) до 407 гигапаскалей (вольфрам).
Для большинства типичных металлов величина этого модуля колеблется от 45 гигапаскалей (магний) до 407 гигапаскалей (вольфрам).
Существует три типа модулей:
- Модуль упругости (модуль Юнга) — отношение продольного напряжения к деформации.
- Модуль сдвига — отношение тангенциальной силы на единицу площади к угловой деформации тела.
- Объемный модуль — отношение напряжения к частичному уменьшению объема тела.
Кривая напряжение-деформация используется для измерения модуля упругости и модуля сдвига. Параметрами, используемыми для описания кривой напряжения-деформации материала, являются предел прочности при растяжении (предел прочности), предел текучести (или предел текучести), удлинение в процентах и уменьшение площади. Модуль упругости имеет ту же размерность, что и напряжение, потому что он получается в результате деления напряжения на деформацию.
Значения модуля упругости для керамических материалов примерно такие же, как для металлов; для полимеров они ниже. Эти различия являются прямым следствием различных типов атомных связей в трех типах материалов. Кроме того, с повышением температуры модуль упругости уменьшается.
Модуль вычисляется путем деления продольного напряжения на деформацию с использованием наклона прямолинейного участка, который находится на кривой напряжения (σ) деформации (ε). В упругой области, в случае, когда наклон берется между двумя точками напряжения-деформации, модуль можно рассматривать как изменение напряжения, деленное на изменение деформации. Модуль = (σ2 — σ1)/(ε2 — ε1), таким образом, напряжение (σ) представляет собой силу, деленную на площадь поперечного сечения образца, а деформация (ε) представляет собой изменение длины материала, деленное на исходную длину материала. .
Модуль упругости является основным свойством, определяющим жесткость материала. В случае автомобильных рессор жесткость играет важную роль в плавности хода и управляемости автомобиля. Жесткость зависит от геометрии. (Также читайте: Влияние коррозии на прочность при растяжении и пластичность материала )
Жесткость зависит от геометрии. (Также читайте: Влияние коррозии на прочность при растяжении и пластичность материала )
Связанный вопрос
Как и зачем измерять прочность защитного покрытия?
Реклама
Синонимы
Модуль упругости, модуль Юнга, модуль
Поделись этим термином
Связанные термины
- Прочность на растяжение
- Стресс
- Предел текучести
- Молоток Шмидта
- Эластичность металла
- Предел упругости
- Упругая деформация
- Модуль Юнга
- Модуль упругости при изгибе
- Модуль упругости при растяжении
Связанное Чтение
- В чем разница между прочностью и вязкостью?
- 3 основных типа разрушающих испытаний материалов
- Как и почему материал ломается
- Влияние концентрации напряжения на распространение трещины
- Понимание взаимосвязи между напряжением и коррозией
- 5 способов измерения твердости материалов
Теги
КоррозияКоррозия 101Научные свойстваИзмерение физических свойствИнжиниринг и составление спецификаций
Актуальные статьи
Покрытия
5 наиболее распространенных типов металлических покрытий, о которых должен знать каждый
Покрытия
4 типа покрытий для бетонных полов (и что следует знать о каждом)
Защита от коррозии
Основы катодной защиты
Трубопровод
В поддержку промывки фосфорной кислотой покрытия труб
Модуль упругости — Руководство AHSS
Модуль упругости (модуль Юнга)
Когда пуансон впервые соприкасается с заготовкой из листового металла, создаваемые силы перемещают атомы листового металла из их нейтрального состояния, и заготовка начинает деформироваться. На атомном уровне эти силы называются упругими напряжениями, а деформация называется упругой деформацией. Силы внутри атомной клетки чрезвычайно сильны: высокие значения упругого напряжения приводят лишь к небольшим величинам упругой деформации. Если сила удаляется, вызывая только упругую деформацию, атомы возвращаются в исходное положение в решетке без остаточной или пластической деформации. Напряжения и деформации теперь на нуле.
На атомном уровне эти силы называются упругими напряжениями, а деформация называется упругой деформацией. Силы внутри атомной клетки чрезвычайно сильны: высокие значения упругого напряжения приводят лишь к небольшим величинам упругой деформации. Если сила удаляется, вызывая только упругую деформацию, атомы возвращаются в исходное положение в решетке без остаточной или пластической деформации. Напряжения и деформации теперь на нуле.
Кривая напряжение-деформация отображает напряжение по вертикальной оси, а деформация — по горизонтальной оси (см. рис. 2 в разделе «Механические свойства»). В начале этой кривой все металлы имеют характерную линейную зависимость между напряжением и деформацией. В этой линейной области наклон упругого напряжения в зависимости от упругой деформации называется Модуль упругости или Модуль Юнга или Модуль упругости и обычно обозначается аббревиатурой E. На этом участке кривой напряжение-деформация существует пропорциональная зависимость между напряжением и деформацией; деформация становится непропорциональной с началом пластической (остаточной) деформации (см. рис. 1).
рис. 1).
Рисунок 1: Модуль упругости представляет собой наклон кривой напряжения-деформации до начала пластической деформации.
Наклон линии модуля зависит от атомной структуры металла. Большинство сталей имеют элементарную атомную ячейку из девяти атомов железа — по одному в каждом углу куба и один в центре куба. Это описывается как объемно-центрированная кубическая структура (BCC). Обычное значение уклона стали составляет 210 ГПа (30 миллионов фунтов на квадратный дюйм). Напротив, алюминий и многие другие цветные металлы имеют 14 атомов как часть элементарной атомной ячейки — по одному на каждом углу куба и по одному на каждой грани куба. Это называется гранецентрированной кубической (FCC) атомной структурой. Многие алюминиевые сплавы имеют модуль упругости примерно 70 ГПа (10 миллионов фунтов на квадратный дюйм).
При полной нагрузке пресса в нижней мертвой точке деформированная форма панели является результатом сочетания упругого напряжения и деформации и пластического напряжения и деформации. Устранение формирующих сил позволяет упругому напряжению и деформации вернуться к нулю. Остаточная деформация заготовки из листового металла представляет собой формованную часть, выходящую из пресса, при этом снятие упругого напряжения и деформации является основной причиной явления неблагоприятной формы, известного как пружинение. Сведение к минимуму или устранение пружинения имеет решающее значение для достижения постоянной формы и размеров штамповки.
Устранение формирующих сил позволяет упругому напряжению и деформации вернуться к нулю. Остаточная деформация заготовки из листового металла представляет собой формованную часть, выходящую из пресса, при этом снятие упругого напряжения и деформации является основной причиной явления неблагоприятной формы, известного как пружинение. Сведение к минимуму или устранение пружинения имеет решающее значение для достижения постоянной формы и размеров штамповки.
В зависимости от конструкции панели и процесса некоторые упругие напряжения не могут быть устранены при снятии вытяжной панели с вытяжного пресса. Упругое напряжение, остающееся в штамповке, называется остаточным напряжением или захваченным напряжением. Любое дополнительное изменение состояния штампованной панели (например, обрезка, пробивка отверстий, сварка скоб, изменение формы или другая пластическая деформация) может изменить величину и распределение остаточных напряжений и, следовательно, потенциально изменить форму и размеры штамповки.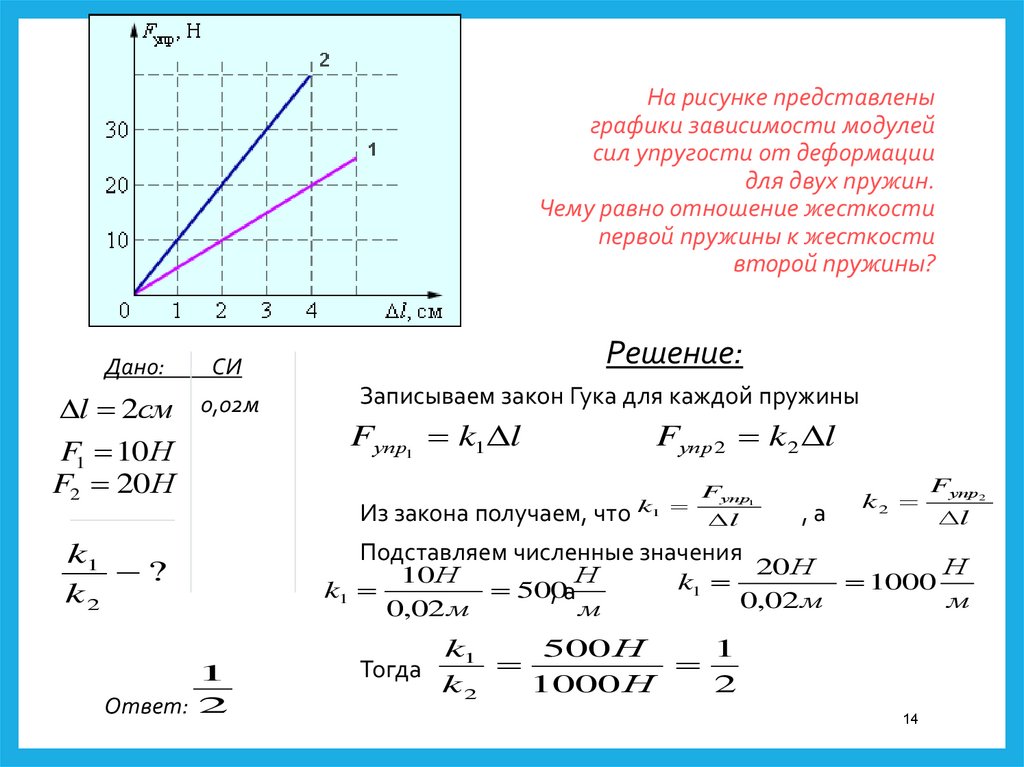
Величина пружинения обратно пропорциональна модулю упругости. Следовательно, при одном и том же пределе текучести сталь с модулем упругости, в три раза превышающим модуль алюминия, будет иметь упругую отдачу в три раза меньше.
Изменение и ухудшение модуля упругости
Аналитики часто рассматривают модуль упругости как константу. Однако модуль упругости изменяется в зависимости от ориентации относительно направления прокатки (рис. 2). Дело осложняется тем, что этот эффект меняется в зависимости от выбранной марки металла.
Рисунок 2: Модуль упругости как функция ориентации для нескольких марок стали (волокнистая сталь, DP 590, DP 980, DP 1180 и MS 1700) D-11
Эффект Баушингера приводит к изменению модуля упругости и, следовательно, влияет на пружинение. Модуль упругости, определенный в нагруженной части кривой напряжения-деформации, отличается от определенного в разгрузочной части. Кроме того, увеличение предварительной деформации снижает модуль упругости, что существенно влияет на точность моделирования деформации и пружинения.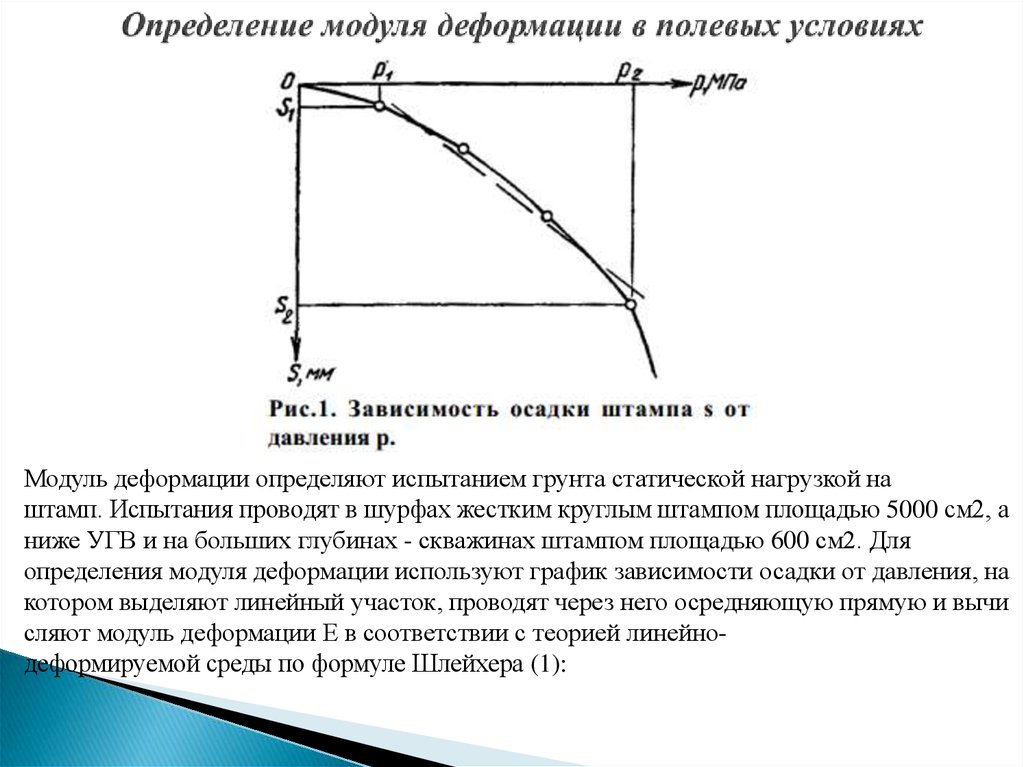

 Ф. Нелинейная упругость // Математическое моделирование систем и процессов. 2001. №9. С. 177–185.
Ф. Нелинейная упругость // Математическое моделирование систем и процессов. 2001. №9. С. 177–185.