Формула коэффициента сжимаемости: Сжимаемость пластовой нефти — Что такое Сжимаемость пластовой нефти?

Коэффициент сжимаемости, формула и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Коэффициенты Коэффициент сжимаемости

Определение и формула коэффициента сжимаемости

Сжимаемостью называют свойство материи к изменению объема под воздействием равномерного внешнего давления. Характеристикой сжимаемости является коэффициент сжимаемости. Его так же называют коэффициентом сжатия, коэффициентом всестороннего сжатия, коэффициентом объемного упругого расширения. Сжимаемость является важной характеристикой вещества, так как она дает возможность судить о зависимости физических свойств от расстояний между его атомами (молекулами).

Обозначения коэффициента сжимаемости могут быть различными, чаще всего встречаются: . В математической форме определение коэффициента сжимаемости запишем как:

   

где знак минус означает, что рост давления ведет к уменьшению объема и наоборот.

Перейдя к дифференциалам коэффициент сжимаемости, будет определен как:

   

Коэффициент сжимаемости можно выразить через такую характеристику вещества как плотность ():

   

В механике грунтов коэффициент сжимаемости определяют как:

   

где — коэффициент пористости. Знак минус указывает на то, что увеличение давления ведет к уменьшению пористости.

Коэффициент сжимаемости зависит от вида вещества (его природы), температуры, давления. Кроме того, процесс в котором происходит сжатие, так же влияет на величину рассматриваемого коэффициента. Поэтому часто индексом обозначают процесс, например, изотермический, коэффициент сжатия при этом называют изотермическим коэффициентом сжатия ():

   

где частная производная от объема взята при постоянной температуре.

Коэффициенты сжимаемости для твердых тел, жидкостей и газов

Эмпирически полученные результаты коэффициентов сжимаемости твердых тел отражают периодическую зависимость от атомного веса элемента. Сжимаемость твердого тела можно определять при помощи измерения линейной деформации твердого тела под гидростатическим давлением. Для изотропного тела коэффициент линейной сжимаемости находят как:

   

где L — линейный размер тела.

У жидкостей сжимаемость существенно меньше, чем у газов. Это видно из кривой уравнения Ван-дер-Ваальса. На рис.1 жидкой фракции вещества соответствует участок AB. Крутизна данного участка говорит о том, что производная является малой величиной, следовательно, мал коэффициент .

Рис. 1

Коэффициент сжимаемости жидкостей лежит в пределах интервала: . Наибольшую сжимаемость среди жидкостей имеет жидкий гелий. Коэффициент сжимаемости зависит от давления и уменьшается с ростом давления. При обычных давлениях коэффициенты сжимаемости разных жидкостей существенно различны, тогда как при высоких давлениях величины всех жидкостей почти одинаковы. Коэффициент сжимаемости жидкости зависит от температуры: коэффициент сжимаемости увеличивается при росте температуры (исключение составляет вода). Для жидкостей используют следующую эмпирическую формулу вычисления коэффициента сжимаемости:

   

где A — некоторая функция температуры, p — внешнее давление, — давление, связанное с силами Ван-дер-Ваальса при температуре T. Выражение (7) является приближенной и используется для ограниченной области давлений. Сжимаемость растворов уменьшается при росте концентрации.

При давлениях близких к атмосферному сжимаемостью жидкости в гидравлических расчетах часто пренебрегают и учитывают ее только в особенных случаях, например, рассматривая явление гидроудара.

Изотермический коэффициент сжимаемости идеального газа равен:

   

Сжимаемость газа велика, в сравнении с жидкостями и твердыми телами.

Единицы измерения

Основной единицей измерения коэффициента сжимаемости в системе СИ является:

   

В СГС:

=см2/дин

Примеры решения задач



Понравился сайт? Расскажи друзьям!


Коэффициент сжимаемости воздуха: таблица и значения

Коэффициент сжимаемости воздуха – это показатель степени сжимаемости воздуха в зависимости от давления и температуры.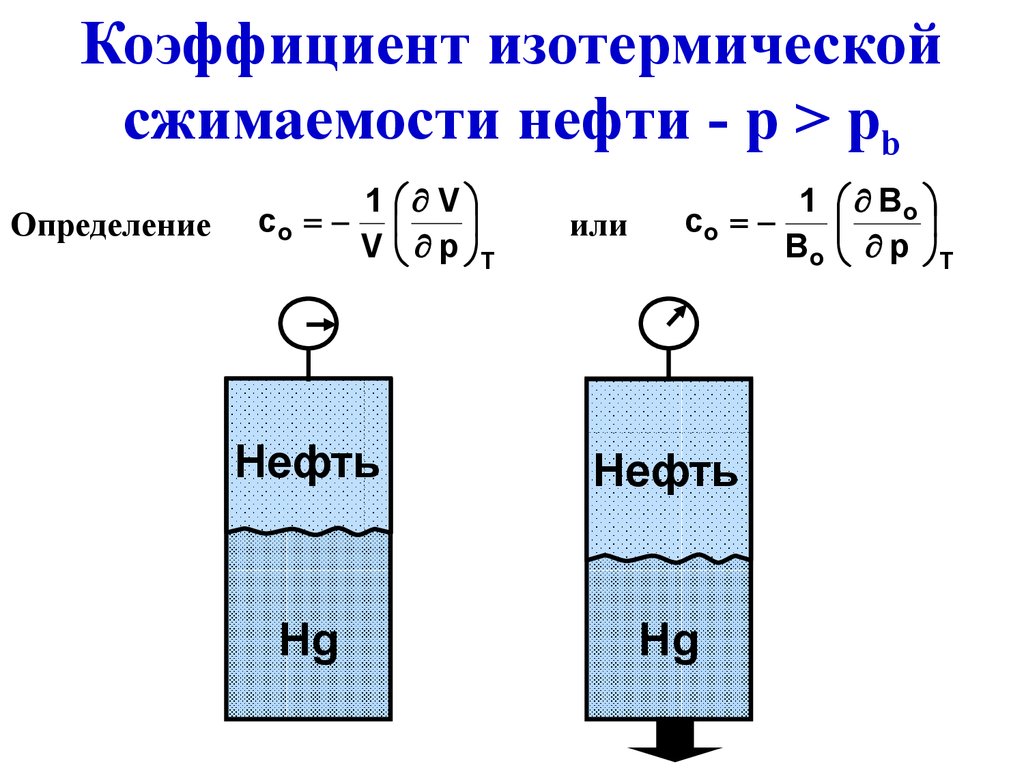 Используется при проведении расчетов параметров работы в средствах индивидуальной защиты органов дыхания. Обозначается: Ксж.

Коэффициент сжимаемости воздуха (далее – коэффициент) используется при расчете времени работы в средствах индивидуальной защиты органов дыхания и зрения (далее – СИЗОД), и предназначен для определения реального объема закачанного в баллоны воздуха.

где:

Vвозд – реальный объем сжатого воздуха в баллонах, л;

Vб – объем баллонов, л;

P – давление в баллонах, атм.

Коэффициент при любых условиях расчета параметров работы в СИЗОД принимается равным 1,1.

Таким образом, зная реальный запас воздуха в баллонах, можно легко вычислить время работы газодымозащитника в СИЗОД. Для этого достаточно разделить реальный запас воздуха на его расход газодымозащитником (в общем случае принимается среднее значение – 40 л/мин):

В общем же виде эта формула приобретает вид:

И в такой трактовке приводится в методических указаниях по проведению расчетов параметров работы в СИЗОД.

Физические основы

Сжимаемость характеризует свойство воздуха изменять свой объем и плотность при изменении давления и температуры. Если вещество в процессе сжатия не испытывает химических, структурных и других изменений, то при возвращении внешнего давления к исходному значению начальный объём восстанавливается.

Термин «сжимаемость» также используется в термодинамике для описания отклонений термодинамических свойств реальных газов от свойств идеальных газов. Коэффициент сжимаемости определяется как:

где:

p – давление газа;

T – температура;

V – молярный объём.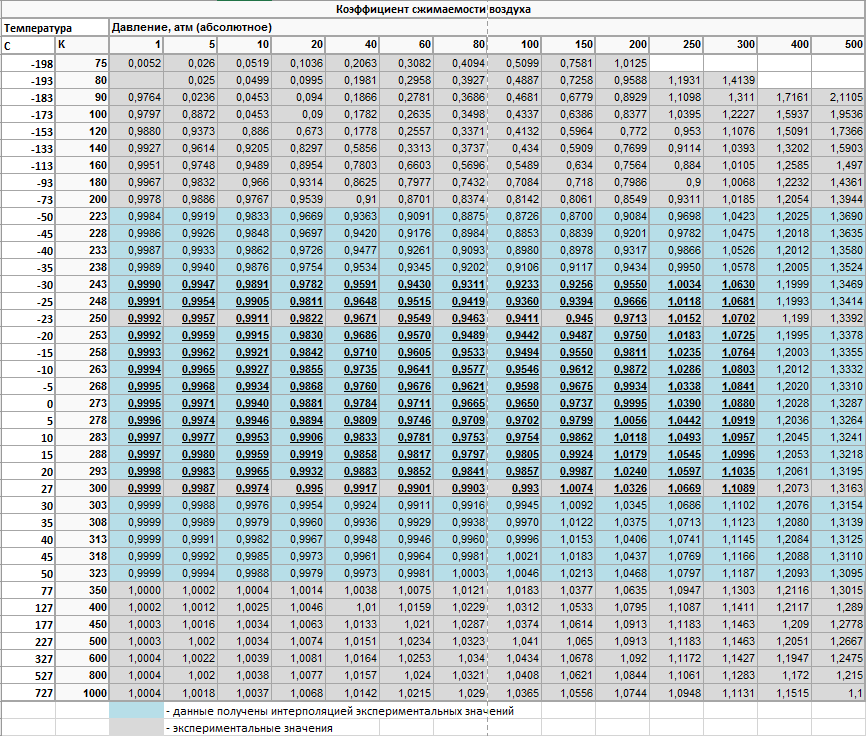

Коэффициент зависит как от температуры вещества, так и от давления. Таким образом, при давлениях 200 атм и 300 атм коэффициент будет разным. При этом даже при различной температуре воздуха коэффициент так же меняется!

Таблица значений коэффициента

Значения коэффициента сжимаемости воздуха при различных давлениях и температурах

Примечание:

  • голубой цвет – данные получены интерполяцией экспериментальных значений;
  • серый цвет – экспериментальные значения;
  • жирным текстом с подчеркиванием выделены значения наиболее интересные с точки зрения ГДЗС.

Зависимость коэффициента сжимаемости воздуха от давления (по оси X, атм.) и температуры (согласно графиков)

Скачать таблицу и график зависимости коэффициента сжимаемости воздуха в формате Microsoft Excel

Из приведенной информации видно, что в большинстве интересующих ГДЗС случаев, коэффициент отличается от единицы на тысячные доли, что может быть пренебрежимо.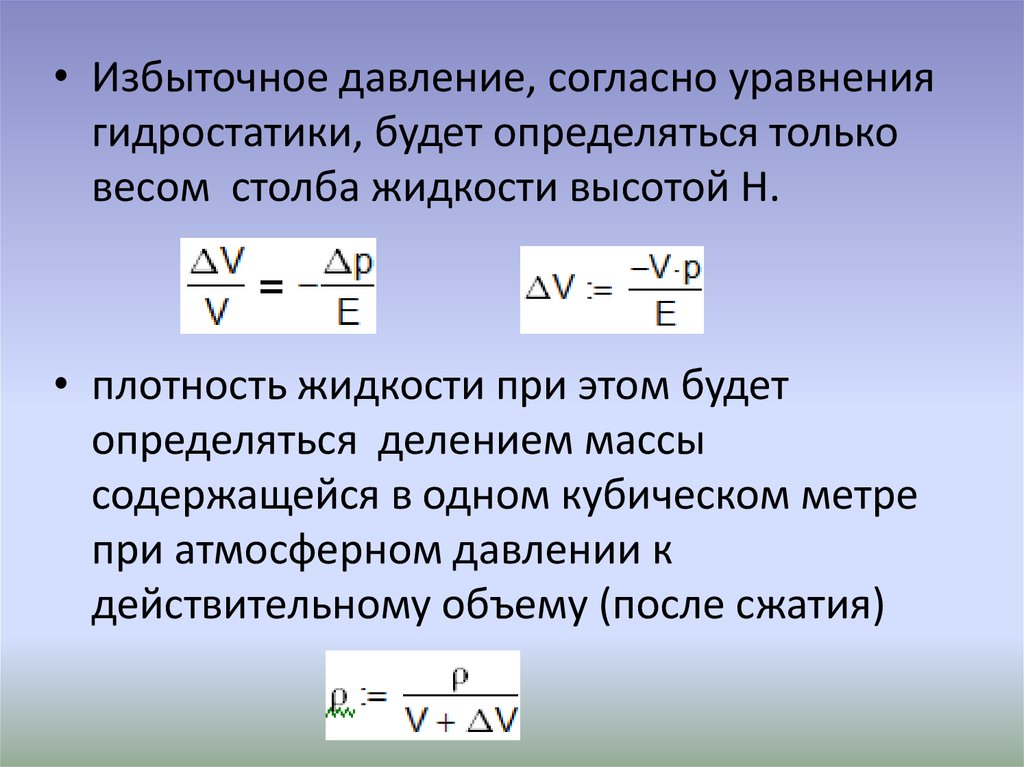 И только при давлениях приближающихся к 300 атмосферам, он начинает увеличиваться и приближаться к 1,1 используемому в расчетах.

Важно понимать, что расчет реального запаса сжатого воздуха уместно делать только в момент, когда баллон только что был наполнен, так как в дальнейшем при работе в аппарате, воздух расходуется, давление в баллонах уменьшается, а следовательно и коэффициенты изменяются. Именно поэтому, сейчас, при расчетах для ДАСВ коэффициент принимается равным 1,1 (так как рабочее давление баллонов достигает 300 атм) при любых условиях, а для ДАСК – 1 (давление баллонов не превышает 200 атм). По этой же причине ранее, в расчетах, для дыхательных аппаратов АИР-2, коэффициент принимался 1 – так как рабочее давление в баллонах данного ДАСВ было 200 атм.

Источники:

  1. Методические указания по проведению расчетов параметров работы в средствах индивидуальной защиты органов дыхания и зрения.
  2. Основные параметры и свойства воздуха в атмосфере.
  3. Большая советская энциклопедия: сжимаемость.
  4. Коэффициент сжимаемости (en).

4.3: Сжимаемость и расширяемость — Химия LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    84310
    • Патрик Флеминг
    • Калифорнийский государственный университет Ист-Бэй

    Изотермическая сжимаемость (\(\kappa_T\))

    Очень важным свойством вещества является его сжимаемость. Газы очень сжимаемы, поэтому при воздействии высокого давления их объемы значительно уменьшаются (вспомните закон Бойля!). Однако твердые и жидкие вещества не так сжимаемы. Однако они не являются полностью несжимаемыми! Высокое давление приведет к уменьшению объема, даже если оно будет незначительным. И, конечно же, одни вещества более сжимаемы, чем другие.

    Чтобы количественно определить, насколько сжимаемы вещества, необходимо определить это свойство. Изотермическая сжимаемость определяется относительным дифференциальным изменением объема из-за изменения давления.

    \[ \kappa_T \equiv — \dfrac{1}{V} \left( \dfrac{\partial V}{\partial p} \right)_T \label{compress}\]

    Знак минус важен чтобы сохранить значение \(\kappa_T\) положительным, так как увеличение давления приведет к уменьшению объема. Термин \(1/V\) необходим для того, чтобы сделать свойство интенсивным, чтобы его можно было удобно свести в таблицу.

    Изобарический коэффициент теплового расширения (\(\alpha\))

    Еще одним очень важным свойством вещества является то, как его объем будет реагировать на изменения температуры. Опять же, газы сильно реагируют на изменения температуры (вспомните закон Чарльза!), тогда как твердые и жидкие вещества будут иметь более умеренную (но не пренебрежимо малую) реакцию на изменения температуры. (Например, если бы ртуть или спирт не расширялись при повышении температуры, мы не смогли бы использовать эти вещества в термометрах.)

    Определение изобарного теплового расширения (или иногда называемого коэффициентом расширения) равно

    \[ \alpha \equiv \dfrac{1}{V} \left( \dfrac{\partial V}{\partial T} \right)_p \label{expand}\]

    Как и в случае с коэффициентом сжимаемости, член \(1/V\) необходим для того, чтобы сделать свойство интенсивным и, таким образом, его можно было удобно свести в таблицу. В случае расширения объем имеет тенденцию увеличиваться с повышением температуры, поэтому частная производная положительна.

    Получение выражения для частной производной (тип I): правило взаимности

    Рассмотрим систему, которая описывается тремя переменными и для которой можно написать математическое ограничение на переменные

    \[F(x, y , z) = 0\]

    В этих условиях можно задавать состояние системы, изменяя независимо только два параметра, так как третий параметр будет иметь фиксированное значение. Таким образом, можно определить две функции: \(z(x, y)\) и \(y(x,z)\).

    Это позволяет записать полные дифференциалы для \(dz\) и \(dy\) следующим образом

    \[dz = \left( \dfrac{\partial z}{\partial x} \right)_y dx + \left( \dfrac{\partial z}{\partial y} \right)_x dy \label{eq5}\]

    и

    \[dy= \left( \dfrac{\ partial y}{\ partial x} \right)_z dx + \left( \dfrac{\partial y}{\partial z} \right)_x dz \label{eq6}\]

    Подстановка выражения \ref{eq6} уравнения в уравнение \ref {eq5}:

    \[ \begin{align} dz &= \left( \dfrac{\partial z}{\partial x} \right)_y dx + \left( \dfrac{\partial z}{\partial y} \right)_x \left[ \left( \dfrac{\partial y}{\partial x} \right)_z dx + \left( \dfrac{\partial y}{\partial z} \right)_x dz \right] \\[4pt] &= \left( \dfrac{\partial z}{\partial x} \right)_y dx + \left( \dfrac{\partial z}{\partial y} \right)_x \left( \dfrac{\partial y}{\partial x} \right)_z dx + \left( \dfrac{\partial z}{\partial y} \right)_x \left( \dfrac{\partial y} {\ partial z} \ right) _x dz \ label {eq 7} \end{выравнивание}\]

    Если система претерпевает изменения по пути, где \(x\) остается постоянным (\(dx = 0\)), это выражение упрощается до

    \[dz = \left( \dfrac{\partial z} {\partial y} \right)_x \left( \dfrac{\partial y}{\partial z} \right)_x dz\]

    И так для изменений, для которых \(dz \neq 0\),

    \[\left( \dfrac{\partial z}{\partial y} \right)_x = \dfrac{1}{\left( \dfrac{\partial y}{\partial z} \right)_x} \]

    Это правило взаимности очень удобно при работе с частными производными. Но его также можно вывести прямолинейным, хотя и менее строгим образом. Начните с записи полного дифференциала для \(z(x,y)\) (уравнение \ref{eq5}):

    \[dz = \left( \dfrac{\partial z}{\partial x} \right)_y dx + \left( \dfrac{\partial z}{\partial y} \right)_x dy \]

    Теперь разделите обе части на \(dz\) и ограничьтесь константой \(x\).

    \[\left.\dfrac{dz}{dz} \right\rvert_{x} = \left( \dfrac{\partial z}{\partial x} \right)_y \left.\dfrac{dx} {dz} \right\rvert_{x} + \left( \dfrac{\partial z}{\partial y} \right)_x \left.\dfrac{dy}{dz} \right\rvert_{x} \label {eq10}\]

    Заметим, что

    \[\left.\dfrac{dz}{dz} \right\rvert_{x} =1\]

    \[ \left.\dfrac{dx}{dz} \right\rvert_{x} = 0\]

    и

    \[\left.\dfrac{dy}{dz} \right\rvert_{x } = \left( \dfrac{\partial y}{\partial z} \right)_{x}\]

    Уравнение \ref{eq10} принимает вид

    \[ 1= \left( \dfrac{\partial z }{\partial y} \right)_z \left( \dfrac{\partial y}{\partial z} \right)_x \]

    или

    \[ \left( \dfrac{\partial z}{\ частичное y} \right)_z = \dfrac{1}{\left( \dfrac{\partial y}{\partial z} \right)_x} \]

    Этот «формальный» метод работы с частными производными удобен и полезно, хотя и не является математически строгим. Однако он работает для частных производных, встречающихся в термодинамике, потому что переменные равны 9.0036 переменные состояния и дифференциалы точные .

    Получение выражения для частной производной (тип II): правило циклической перестановки {\ partial z} {\ partial x} \right) _y dx + \ left( \ dfrac {\ partial z} {\ partial y} \ right) _x \ left ( \ dfrac {\ partial y} {\ partial x} \right)_z dx + \left( \dfrac{\partial z}{\partial y} \right)_x \left( \dfrac{\partial y}{\partial z} \right)_x dz \]

    Если система претерпевает изменения по пути, в котором \(z\) поддерживается постоянным (\(dz = 0\)), это выражение упрощается до

    \[0 = \left( \dfrac{\partial z} {\partial x} \right)_y dy + \left( \dfrac{\partial z}{\partial y} \right)_x \left( \dfrac{\partial y}{\partial x} \right)_z dx \]

    И так для и изменения в которых \(dx \neq 0\)

    \[\left( \dfrac{\partial z}{\partial x} \right)_y = — \left( \dfrac{ \partial z}{\partial y} \right)_x \left( \dfrac{\partial y}{\partial x} \right)_z \]

    Это правило циклической перестановки очень удобно при работе с частными производными. Но его также можно вывести прямолинейным, хотя и менее строгим образом. Как и в приведенном выше выводе, мы начнем с записи полного дифференциала \(z(x,y)\)

    \[dz = \left( \dfrac{\partial z}{\partial x} \right)_y dx + \left( \dfrac{\partial z}{\partial y} \right)_x dy \]

    Теперь разделите обе части на \(dx\) и ограничьтесь константой \(z\).

    \[\left.\dfrac{dz}{dx} \right\rvert_{z} = \left( \dfrac{\partial z}{\partial x} \right)_y \left.\dfrac{dx} {dx} \right\rvert_{z} + \left( \dfrac{\partial z}{\partial y} \right)_x \left.\dfrac{dy}{dx} \right\rvert_{z} \label {eq21} \]

    Обратите внимание, что

    \[\left.\dfrac{dz}{dx} \right\rvert_{z} =0\]

    \[ \left.\dfrac{dx}{dx} \right\rvert_{ z} =1\]

    и

    \[\left.\dfrac{dy}{dx} \right\rvert_{z} = \left(\dfrac{\partial y}{\partial x} \right) _{z}\]

    Уравнение \ref{eq21} принимает вид

    \[ 0 = \left( \dfrac{\partial z}{\partial x} \right)_y + \left( \dfrac{\partial z }{\partial y} \right)_x \left( \dfrac{\partial y}{\partial x} \right)_{z} \]

    , которое легко преобразовать в

    \[ \left( \dfrac{\partial z}{\partial x} \right)_y = — \left( \dfrac{\partial z}{\partial y} \right)_x \left( \dfrac{ \partial y}{\partial x} \right)_{z} \]

    Этот тип преобразования очень удобен и будет часто использоваться при работе с частными производными в термодинамике.

    Пример \(\PageIndex{1}\): расширение термодинамических функций

    Получите выражение для

    \[\dfrac{\alpha}{\kappa_T}. \label{e1}\]

    в терминах производных термодинамических функций, используя определения в уравнениях \ref{compress} и \ref{expand}.

    Решение

    Подстановка уравнений \ref{compress} и \ref{expand} в уравнение \ref{e1}

    \[\dfrac{\alpha}{\kappa_T}= \dfrac{\dfrac{1 }{V} \left( \dfrac{\partial V}{\partial T} \right)_p}{- \dfrac{1}{V} \left( \dfrac{\partial V}{\partial p} \ right)_T} \nonumber\]

    Упрощение (удаление членов \(1/V\) и использование преобразования типа I для обращения частной производной в знаменателе) дает

    \[\dfrac{\alpha}{\kappa_T } = — \left( \dfrac{\partial V}{\partial T} \right)_p \left( \dfrac{\partial p}{\partial V} \right)_T \nonumber\]

    Применение преобразования типа II дает окончательный результат:

    \[ \dfrac{\alpha}{\kappa_T} = \left( \dfrac{\partial p}{\partial T} \right)_V \nonumber \]​​

    Эта страница под заголовком 4. 3: Сжимаемость и расширяемость распространяется под лицензией CC BY-NC-SA 4.0, ее автором, ремиксом и/или куратором является Патрик Флеминг.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Патрик Флеминг
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Показать страницу TOC
        нет на странице
      2. Теги
        1. правило циклической перестановки
        2. РАСШИРЕНИЕ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
        3. изобарическое тепловое расширение
        4. изотермическая сжимаемость
        5. взаимное правило

      Калькулятор коэффициента сжимаемости

      Автор Rahul Dhari

      Отзыв Стивена Вудинга

      Последнее обновление: 06 декабря 2021 г.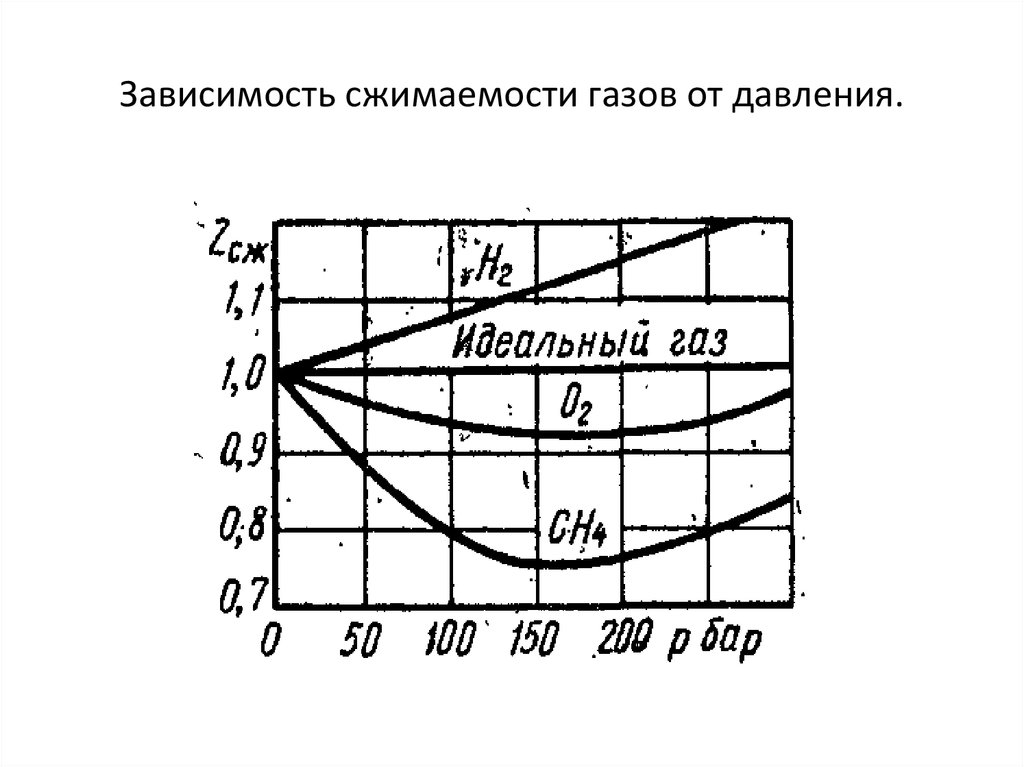

      Содержание:

      • Как определяется коэффициент сжимаемости?
      • Как пользоваться калькулятором коэффициента сжимаемости?
      • Пример: Использование калькулятора коэффициента сжимаемости
      • Часто задаваемые вопросы

      Калькулятор коэффициента сжимаемости определяет коэффициент сжимаемости , используя версию уравнения закона идеального газа, скорректированную для неидеальных газов. Этот фактор полезен для определения масса и объем неидеальных газов . Вы можете получить несколько результатов с помощью калькулятора, чтобы нарисовать диаграмму коэффициента сжимаемости. Читайте дальше, чтобы понять, что такое коэффициент сжимаемости и как его рассчитать.

      Как определяется коэффициент сжимаемости?

      Поведение идеального газа можно обобщить с помощью уравнения, которое мы знаем как закон идеального газа . Однако это уравнение можно применять только в определенных условиях и для газов.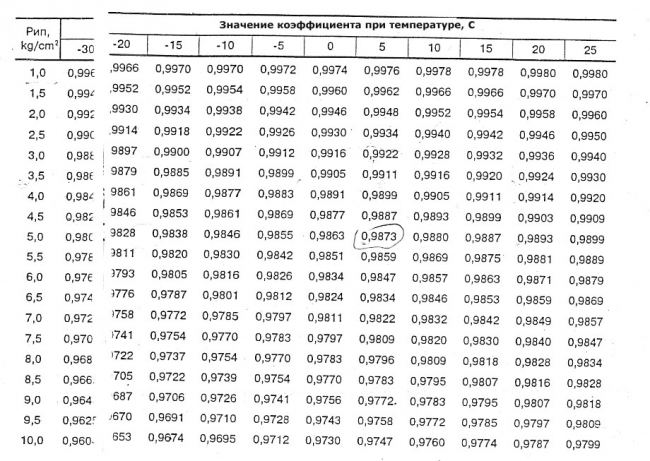 Поэтому это уравнение было изменено для учета поведения реальных газов. Эта операция была выполнена путем включения безразмерный объект , известный как коэффициент сжимаемости, Z . Математически уравнение идеального газа для газа, имеющего объем V и число молей n при давлении P и температуре T с газовой постоянной R , записывается как:

      P * 9 = n * R * T

      Это преобразуется в уравнение коэффициента сжимаемости, где коэффициент сжимаемости Z включен в уравнение:

      Z = P * V / n * R * T

      Коэффициент сжимаемости используется для определения отклонения термодинамических свойств реальных газов от поведения идеального газа. Термин «коэффициент сжимаемости» можно также определить как отношение фактического объема газа к идеальному объему газа при данной температуре и давлении. Математически это:

      Z = V фактическое / V идеальное

      Как использовать калькулятор коэффициента сжимаемости?

      Выполните указанные ниже действия, чтобы рассчитать коэффициент сжимаемости, Z .

      • Шаг 1: Введите давление газа, P .
      • Шаг 2: Введите объем газа, V .
      • Шаг 3: Введите количество вещества в молях, n .
      • Шаг 4: Введите универсальную газовую постоянную, R . Универсальная газовая постоянная устанавливается на значение по умолчанию в единицах СИ, т. е. 8,314 8,314 Дж⋅К⁻¹⋅моль⁻¹. Значение в системе единиц FPS равно 9.0288 10,73164 [psi ft 3 ]/[lbm mol °R] .
      • Шаг 5: Введите температуру газа, T .
      • Шаг 6: Калькулятор теперь будет использовать уравнение коэффициента сжимаемости, чтобы вернуть значение коэффициента сжимаемости.

      Пример: Использование калькулятора коэффициента сжимаемости

      Найдите коэффициент сжимаемости для воздуха 1 бар и 293 K с объемом 1 м 3 . Примите число родинок равным 9.0288 44,6 и газовая постоянная R как 8,314 Дж⋅К⁻¹⋅моль⁻¹ .

      • Шаг 1: Введите давление газа, P = 1 бар .
      • Шаг 2: Укажите объем газа, В = 1 м 3 .
      • Шаг 3: Введите количество вещества в молях, n = 44,6 .
      • Шаг 4: Универсальная газовая постоянная, R устанавливается на 8,314 в качестве значения по умолчанию.
      • Шаг 5: Введите температуру газа, T = 293 K .
      • Шаг 6: Калькулятор теперь будет использовать уравнение коэффициента сжимаемости, чтобы вернуть значение коэффициента сжимаемости.

      z = p * v / n * r * t
      z = 10 5 * 1 / 44,6 * 8.314 * 293 = 0,9204
      Коэффициент компрессии. SA 4.0, через Wikimedia Commons

      Теперь мы знаем, что коэффициент сжимаемости Z для воздуха при вышеуказанных условиях равен 9.0288 0,9204 . Вы также можете прочитать об уравнении Ван-дер-Ваальса, которое также оценивает свойство отклонения газов от идеального поведения. Вы также можете найти коэффициент сжимаемости для нескольких комбинаций температуры и давления, чтобы составить диаграмму коэффициента сжимаемости, пример которой можно увидеть выше.

      Часто задаваемые вопросы

      Что такое коэффициент сжимаемости газа?

      Коэффициент сжимаемости представляет собой отношение фактического объема газа к объему идеального газа.

      Z = P × V / n × R × T = V фактический /V идеальный

      Как рассчитать коэффициент сжимаемости?

      Для расчета коэффициента сжимаемости:

      1. Умножить №. молей по универсальной газовой постоянной и температуре газа.
      2. Разделите давление на предыдущий продукт.
      3. Умножьте на объем газа, чтобы получить коэффициент сжимаемости.

      Z = P × V / n × R × T

      Каково физическое значение коэффициента сжимаемости Z?

      Коэффициент сжимаемости Z представляет собой отклонение свойств реального газа от поведения идеального газа.