Содержание
Относительная деформация, теория и примеры задач
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Физика Относительная деформация
Изменение размеров, объема и возможно формы тела, при внешнем воздействии на него, называют в физике деформацией. Тело деформируется при растяжении, сжатии или (и), при изменении его температуры.
Деформация появляется тогда, когда разные части тела совершают разные перемещения. Так, например, если резиновый шнур тянуть за концы, то разные его части сместятся относительно друг друга, и шнур окажется деформированным (растянется, удлинится). При деформации изменяются расстояния между атомами или молекулами тел, поэтому возникают силы упругости.
При деформации изменяются расстояния между атомами или молекулами тел, поэтому возникают силы упругости.
Пусть прямой брус, длиной и, имеющий постоянное сечение, закреплен одним концом. За другой конец его растягивают, прикладывая силу (рис.1). При этом тело удлиняется на величину , которую называют абсолютным удлинением (или абсолютной продольной деформацией).
В любой точке рассматриваемого тела имеется одинаковое напряженное состояние. Линейную деформацию () при растяжении и сжатии подобных объектов называют относительным удлинением (относительной продольной деформацией):
Относительная продольная деформация
Относительная продольная деформация – величина безразмерная. Как правило относительное удлинение много меньше единицы ().
Деформацию удлинения обычно считают положительной, а деформацию сжатия отрицательной.
Если напряжение в брусе не превышает некоторого предела, экспериментально установлена зависимость:
где – продольная сила в поперечных сечениях бруса; S – площадь поперечного сечения бруса; E – модуль упругости (модуль Юнга) – физическая величина, характеристика жёсткости материала. Принимая о внимание то, что нормальное напряжение в поперечном сечении ():
Принимая о внимание то, что нормальное напряжение в поперечном сечении ():
получим:
Абсолютное удлинение бруса можно выразить как:
Выражение (5) является математической записью закона Р. Гука, который отражает прямую зависимость между силой и деформацией при небольших нагрузках.
В следующей формулировке, закон Гука используется не только при рассмотрении растяжения (сжатия) бруса: Относительная продольная деформация прямо пропорциональна нормальному напряжению.
Относительная деформация при сдвиге
При сдвиге относительную деформацию характеризуют при помощи формулы:
где – относительный сдвиг; – абсолютный сдвиг слоев параллельных по отношению друг к другу; h — расстояние между слоями; – угол сдвига.
Закон Гука для сдвига записывают как:
где G – модуль сдвига, F – сила, вызывающая сдвиг, параллельная сдвигающимся слоям тела.
Примеры решения задач
|
Понравился сайт? Расскажи друзьям! |
| ||
Закон Гука, сила упругости — определение, формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Деформация растяжения
Деформация сжатия
Деформация сдвига
Деформация при кручении
Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука —сила упругости [Н] k — коэффициент жесткости [Н/м] х — изменение длины (деформация) [м] |
Важно раз
Изменение длины может обозначаться по-разному в различных источниках.
Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Важно два
Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Вспомним закон Гука:
И выразим из него модуль удлинения лески:
Так как одна сила уравновешивает другую, мы можем их приравнять:
Подставим числа, жесткость лески при этом выражаем в ньютонах:
= 0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Задачка
Какова жесткость системы из двух пружин, жесткости которых k1 = 100 Н/м, k2 = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
66,7 Н/м
Очень-очень важно!
Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
F = kx
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры:
2 см = 0,02 м
И подставим в формулу:
=100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
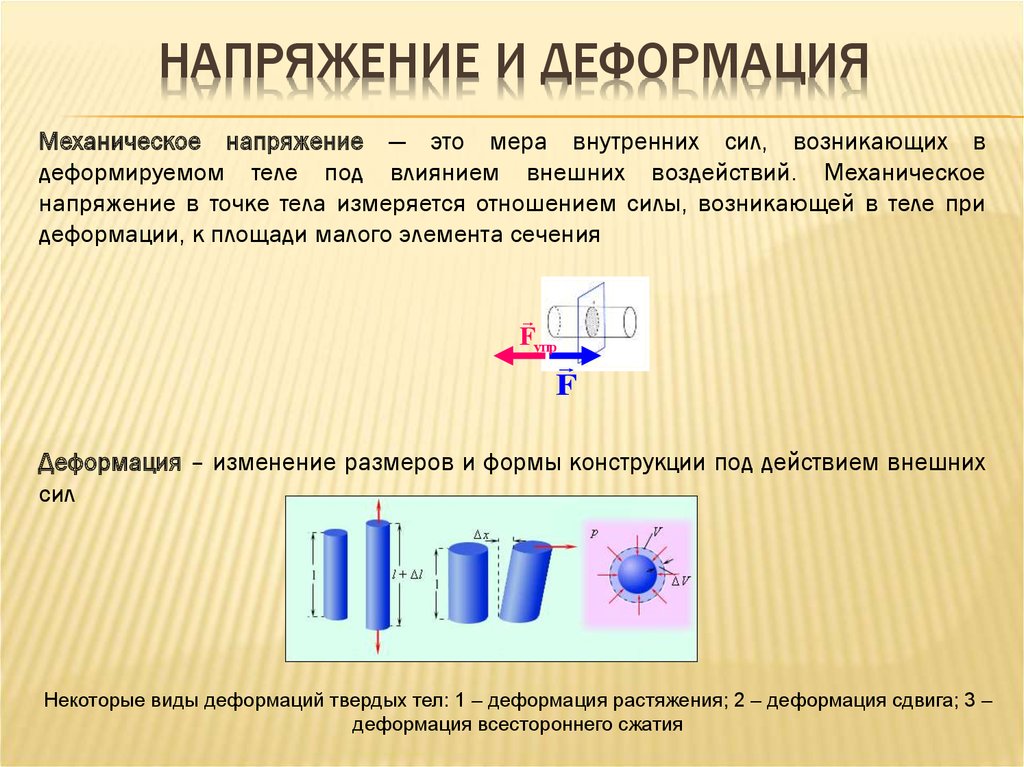
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение представляет собой отношение приложенной силы F к площади поперечного сечения — , определяемой как « силы на единицу площади ».
- растягивающее напряжение — напряжение, стремящееся к растяжению или удлинению материала, — действует нормально к напряженной области
- сжимающее напряжение — напряжение, стремящееся сжать или укоротить материал — действует нормально к напряженной области
- напряжение сдвига — напряжение, стремящееся к сдвигу материала — действует в плоскости напряженной области под прямым углом к сжимающему или растягивающему напряжению
Растягивающее или сжимающее напряжение — нормальное напряжение Плана обычно обозначается «
Нормальное напряжение » или « Прямое напряжение » и может быть выражен как
σ = F N / A (1)
, где
σ = нормальное напряжение (PA (N /M 2 ), PSI (LB F /в 2 ))
F N = нормальная фиксация Perpendicult Perpendicult Perpendicult Perpendicul0.
Perpendicult Perpendicul0. Perpendicul0. к площади (N, LB F )
A = Площадь (M 2 , в 2 )
- A KIP — Императорская установка FIRC f (фунт-сила)
- 1 килофунт = 4448,2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)
Нормальная сила действует перпендикулярно площади и развивается всякий раз, когда внешние нагрузки стремятся толкать или тянуть два сегмента тела.
Пример. Сила растяжения, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как
σ = (10 10 3 Н) / (π ((10 10 -3 M) / 2) 2 )
= 1273888535 (N / M 2 )
= 127 (MPA)
Пример — сила, действуя на Douglas.
Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 в столбе из пихты Дугласа.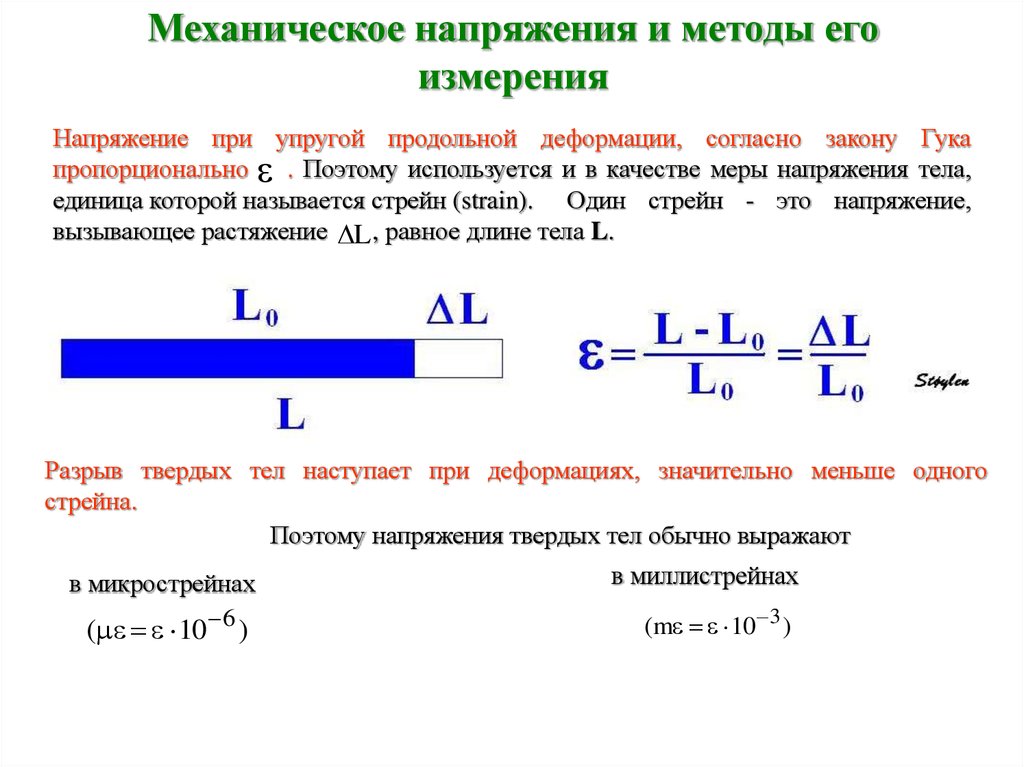 Размер поста после обработки составляет 5,5 x 5,5 дюйма , а сжимающее напряжение можно рассчитать как
Размер поста после обработки составляет 5,5 x 5,5 дюйма , а сжимающее напряжение можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюйма) (5,5 дюйма) )
= 991 (фунт/в 2 , PSI)
Сдвиг Пресс. τ = F
p / A (2)
where
τ = shear stress (Pa (N/m 2 ), psi (lb f /in 2 ))
F p = поперечная сила в плоскости площади (Н, фунт f )
A = площадь (м 2 , in 2 ) 9007 сила сдвига A 7
8 900 лежит в плоскость области и развивается, когда внешние нагрузки имеют тенденцию заставлять два сегмента тела скользить друг по другу.
Деформация (деформация)
Деформация определяется как «деформация твердого тела под действием напряжения».
- Нормальная деформация — удлинение или сокращение отрезка линии
- Shear strain — change in angle between two line segments originally perpendicular
Normal strain and can be expressed as
ε = dl / l o
= σ / E (3)
где
dl = изменение длины (м, дюйм)
l o = начальная длина (м, дюйм)0011
E = модуль Юнга (модуль упругости) (Па , (Н/м 2 ), фунт/кв.
дюйм (фунт f / дюйм 2 )) прогнозировать удлинение или сжатие объекта под действием силы
Обратите внимание, что деформация является безразмерной единицей, поскольку она представляет собой отношение двух длин. Но также общепринято указывать это как отношение двух единиц длины — например, м/м или дюймов/дюйм 9.0006 .
- Коэффициент Пуассона представляет собой относительную деформацию сжатия
Пример. Напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и изготовлен из стали с модулем упругости 200 ГПа (200·10 9 Н/м 2 ) . Изменение длины можно рассчитать путем преобразования (3) в
dl = σ l o / E
= (127 10 6 PA) (2 м) / (200 10 9 PA)
= 0,00127 M
= 1,27 мм
- Как вычислять Radial Compraction
- .
Энергия деформации
Напряжение объекта накапливает в нем энергию. Для осевой нагрузки накопленная энергия может быть выражена как
U = 1/2 F n dl
, где
U = энергия деформации (Дж (Н·м), фут-фунт)
Модуль Юнга — модуль упругости (или модуль упругости) — закон Гука
Большинство металлов деформируется пропорционально приложенной нагрузке в диапазоне нагрузок. Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .
E = напряжение / деформация0007 = (F N / A) / (DL / L O ) (4)
Где
E = Модуль Young’s (N / M 2 ) (LB / в 2 , psi)
Модуль упругости, или модуль Юнга, обычно используется для металлов и металлических сплавов и выражается в единицах или Па . Модуль упругости при растяжении часто используется для пластмасс и выражается в терминах 10 5 фунт f /in 2 или ГПа .
Модуль сдвига эластичности — или модуль жесткости
g = напряжение / напряжение
= τ / γ
= (F P / A) / (S P / A) / A) / (S P / A) / S) / A) / A) / S) / A) / S) / A) / S) / A) / S) / S) / A) / S) / A) / S) / A) / S) / A) / S) / A). / d) (5)
, где
G = модуль упругости при сдвиге или модуль жесткости (Н/м 2 ) (lb/in 2 , psi)
τ = shear stress ((Pa) N/m 2 , psi)
γ = единица меньшей меры деформации сдвига
F P = Сила параллельна лицам, которые они действуют
A = область (M 2 , в 200944)
4 2 , в 2 )
44 с = смещение граней (м, дюйм)
d = расстояние между смещенными поверхностями (м, дюймы)
- Пластичные и хрупкие материалы
Объемный модуль упругости
Объемный модуль упругости — или объемный модуль — является мерой сопротивления вещества равномерное сжатие.
Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Модули упругости
Модули упругости для некоторых распространенных материалов:
Material Young’s Modulus
— E —Shear Modulus
— G —Bulk Modulus
— K —(GPa)
(10 6 psi)(GPa)
(10 6 psi)(GPa)
(10 6 psi)Aluminum 70 24 70 Brass 91 36 61 Copper 110 42 140 Glass 55 23 37 Iron 91 70 100 Lead 16 5. 6
7.7 92) или паскаль. Наиболее часто используемой единицей напряжения является паскаль, который представляет собой силу в 1 Н, воздействующую на единицу площади.
- 1 Паскаль = 1 Н/м 2
Однако это довольно маленькая единица для большинства инженерных задач, поэтому удобно работать с кратными паскалю: ГПа , а МПа .
- 1 МПа 10 6 Н/м 2
- 1 ГПа 10 9 Н/м 2
Предел прочности при растяжении (UTS) материала — это сила, приходящаяся на единицу площади, при которой он разрывается на две части. Растягивающее напряжение — это такой тип напряжения, при котором два участка материала по обе стороны от плоскости напряжения стремятся разойтись или удлиниться. Способность материала или конструкции выдерживать нагрузки, имеющие тенденцию к удлинению, известна как предел прочности при растяжении (UTS) .
Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0031 нормальные напряжения .
Деформация представляет собой безразмерную величину, которая выражает пропорциональное изменение размеров (интенсивность или степень деформации) и измеряется как общая деформация (удлинение) на опорную длину материала из-за некоторого приложенного напряжения.
Ссылки:
Материаловедение:
- Министерство энергетики США, материаловедение. Справочник по основам Министерства энергетики, том 1 и 2.
Январь 1993 г.
- Министерство энергетики США, материаловедение. Справочник по основам Министерства энергетики, том 2 и 2. Январь 1993 г.
- Уильям Д. Каллистер, Дэвид Г. Ретвиш. Материаловедение и инженерия: введение, 9-е издание, Wiley; 9 издание (4 декабря 2013 г.), ISBN-13: 978-1118324578.
- Эберхарт, Марк (2003). Почему все ломается: понимание мира по тому, как он разваливается. Гармония. ISBN 978-1-4000-4760-4.
- Гаскелл, Дэвид Р. (1995). Введение в термодинамику материалов (4-е изд.). Издательство Тейлор и Фрэнсис. ISBN 978-1-56032-992-3.
- Гонсалес-Виньяс, В. и Манчини, Х.Л. (2004). Введение в материаловедение. Издательство Принстонского университета. ISBN 978-0-691-07097-1.
- Эшби, Майкл; Хью Шерклифф; Дэвид Себон (2007). Материалы: инженерия, наука, обработка и дизайн (1-е изд.). Баттерворт-Хайнеманн. ISBN 978-0-7506-8391-3.
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную технику, 3-е изд., Prentice-Hall, 2001, ISBN: 0-201-82498-1.

 Perpendicult Perpendicul0. Perpendicul0. к площади (N, LB F )
Perpendicult Perpendicul0. Perpendicul0. к площади (N, LB F )  дюйм (фунт f / дюйм 2 )) прогнозировать удлинение или сжатие объекта под действием силы
дюйм (фунт f / дюйм 2 )) прогнозировать удлинение или сжатие объекта под действием силы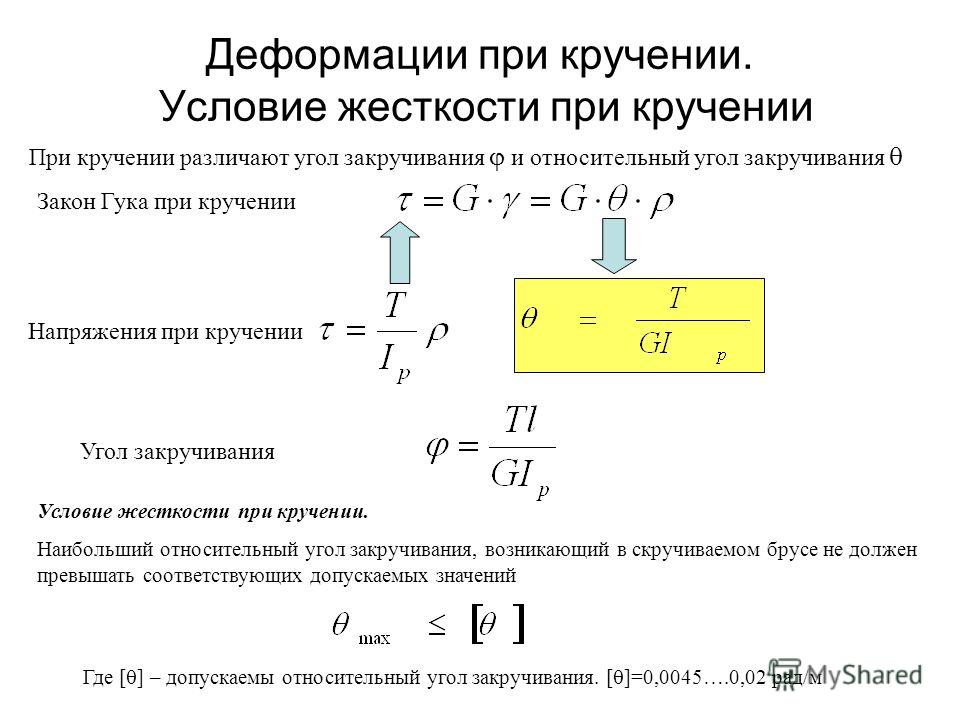

 Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке. 6
6 Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0031 нормальные напряжения .
Предел прочности на растяжение измеряется максимальным напряжением, которое материал может выдержать при растяжении или растяжении до разрыва. При изучении прочности материалов прочность на растяжение, прочность на сжатие и прочность на сдвиг можно анализировать независимо друг от друга. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются 9.0031 нормальные напряжения . Январь 1993 г.
Январь 1993 г.