Единицы измерения деформации: Относительные деформации

Относительная деформация, теория и примеры задач

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Относительная деформация

Изменение размеров, объема и возможно формы тела, при внешнем воздействии на него, называют в физике деформацией. Тело деформируется при растяжении, сжатии или (и), при изменении его температуры.

Деформация появляется тогда, когда разные части тела совершают разные перемещения. Так, например, если резиновый шнур тянуть за концы, то разные его части сместятся относительно друг друга, и шнур окажется деформированным (растянется, удлинится). При деформации изменяются расстояния между атомами или молекулами тел, поэтому возникают силы упругости.

Пусть прямой брус, длиной и, имеющий постоянное сечение, закреплен одним концом. За другой конец его растягивают, прикладывая силу (рис.1). При этом тело удлиняется на величину , которую называют абсолютным удлинением (или абсолютной продольной деформацией).

В любой точке рассматриваемого тела имеется одинаковое напряженное состояние. Линейную деформацию () при растяжении и сжатии подобных объектов называют относительным удлинением (относительной продольной деформацией):

Относительная продольная деформация

Относительная продольная деформация – величина безразмерная. Как правило относительное удлинение много меньше единицы ().

Деформацию удлинения обычно считают положительной, а деформацию сжатия отрицательной.

Если напряжение в брусе не превышает некоторого предела, экспериментально установлена зависимость:

где – продольная сила в поперечных сечениях бруса; S – площадь поперечного сечения бруса; E – модуль упругости (модуль Юнга) – физическая величина, характеристика жёсткости материала. Принимая о внимание то, что нормальное напряжение в поперечном сечении ():

получим:

Абсолютное удлинение бруса можно выразить как:

Выражение (5) является математической записью закона Р. Гука, который отражает прямую зависимость между силой и деформацией при небольших нагрузках.

В следующей формулировке, закон Гука используется не только при рассмотрении растяжения (сжатия) бруса: Относительная продольная деформация прямо пропорциональна нормальному напряжению.

Относительная деформация при сдвиге

При сдвиге относительную деформацию характеризуют при помощи формулы:

где – относительный сдвиг; – абсолютный сдвиг слоев параллельных по отношению друг к другу; h — расстояние между слоями; – угол сдвига.

Закон Гука для сдвига записывают как:

где G – модуль сдвига, F – сила, вызывающая сдвиг, параллельная сдвигающимся слоям тела.

Примеры решения задач

Закон Гука, сила упругости — определение, формулы

Покажем, как применять знание физики в жизни

Начать учиться

200. 1K

Если вы возьмете резиновый шарик и шар из камня и начнете кидать в стену (скучный день выдался, мало ли) — заметите, что они отталкиваются совершенно по-разному. Про силу упругости, которая объясняет этот процесс — в этой статье.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

• Деформация растяжения

• Деформация сжатия

• Деформация сдвига

• Деформация при кручении

• Деформация при изгибе

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Важно раз

Изменение длины может обозначаться по-разному в различных источниках.

Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.

СИ — международная система единиц.

«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Вспомним закон Гука:

И выразим из него модуль удлинения лески:

Так как одна сила уравновешивает другую, мы можем их приравнять:

Подставим числа, жесткость лески при этом выражаем в ньютонах:

= 0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.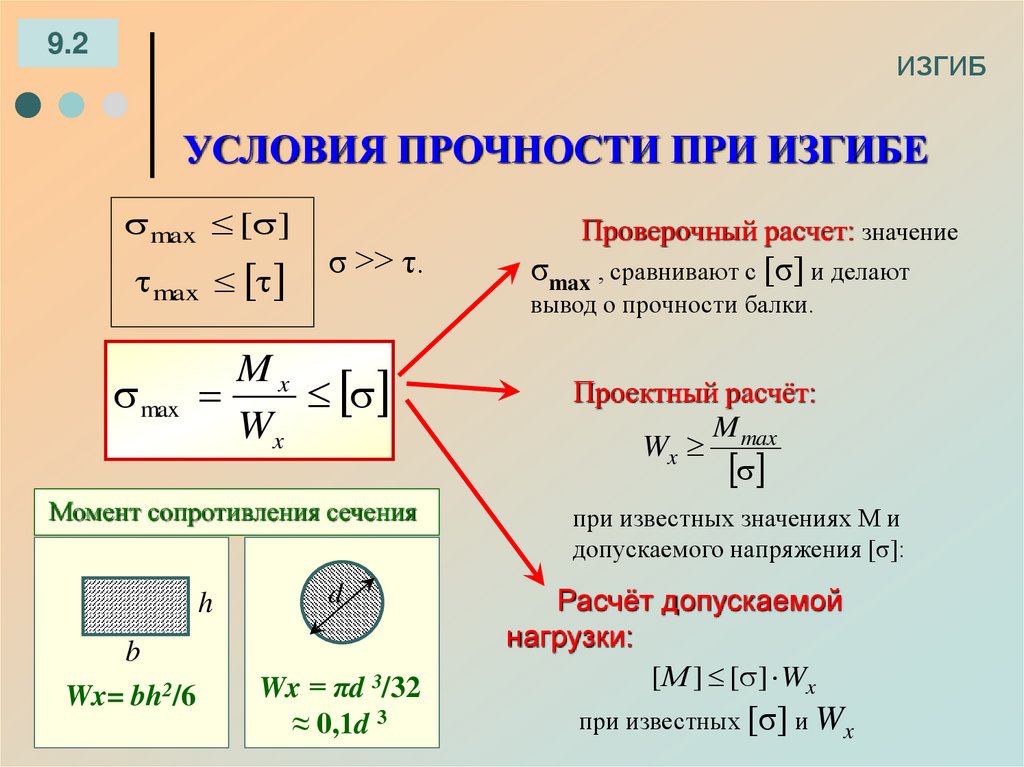

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.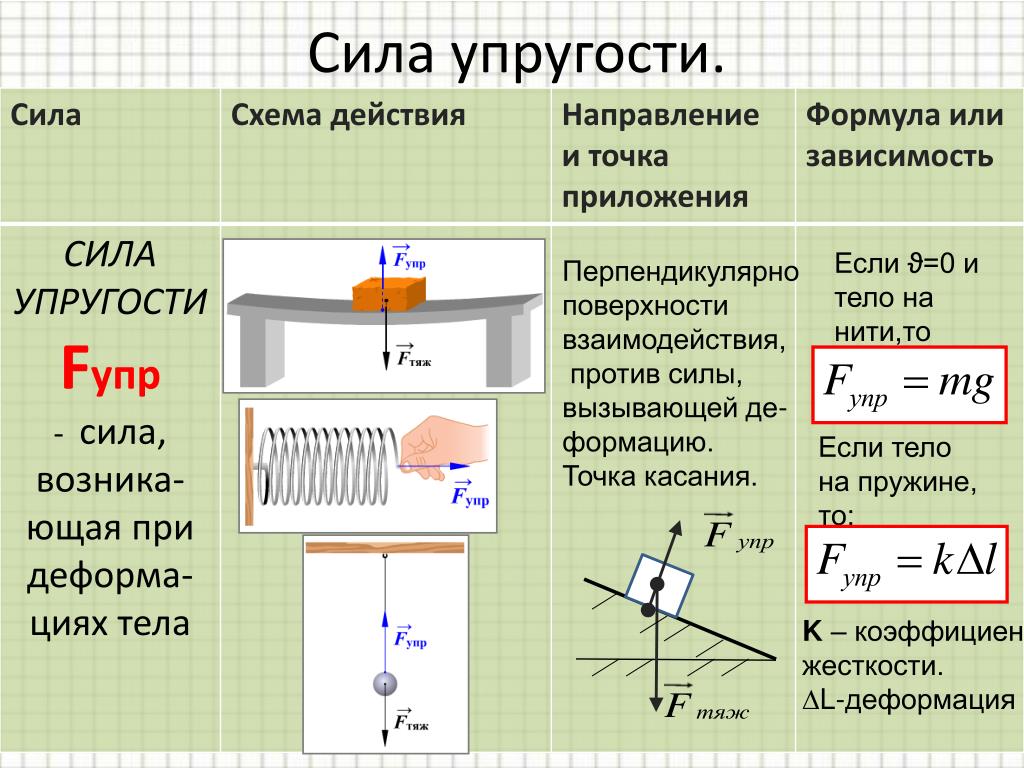

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

66,7 Н/м

Очень-очень важно!

Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:

2 см = 0,02 м

И подставим в формулу:

=100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

Карина Хачатурян

К предыдущей статье

176.5K

Закон электромагнитной индукции

К следующей статье

Момент силы

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Что такое тензодатчик

Что такое тензодатчик? На этой странице будут обсуждаться основы и принципы, составляющие этот очень полезный датчик. -6].

Стресс, деформация и как они связаны между собой

Стресс и деформация сильно связаны друг с другом. В мире экспериментального анализа напряжений мы используем эти связи для расчета приложенного к телу напряжения путем измерения деформации и использования закона Гука.

Закон Гука гласит, что напряжение растяжения ( σ ) линейно пропорционально деформации ( ε ) на модуль упругости ( E ) в области линейной упругости:

Это иллюстрирует необходимость обеспечения высокоточного измерения деформации для выполнения исследований экспериментального анализа напряжения для проверки прочности материалов и структурных конструкций, а также для точного проектирования тензодатчиков, датчиков и Датчики силы с тензодатчиками.

Напряжение, деформация и то, как они связаны друг с другом (продолжение)

Это иллюстрирует необходимость обеспечения высокоточного измерения деформации для выполнения исследований экспериментального анализа напряжения для проверки прочности материалов и структурных конструкций. , а также для точного проектирования тензодатчиков, преобразователей и датчиков силы с тензодатчиками.

Как работает тензодатчик?

Тензорезистор — это компонент, используемый в электрической цепи. Все компоненты в электрической цепи проявляют некоторое сопротивление потоку электрического тока или сопротивление, которое можно измерить электронными приборами. Когда тензорезистор растягивается (или деформируется), его сопротивление изменяется прямо пропорционально деформации. Измеряя изменение электрического сопротивления, также можно узнать деформацию. Это так просто.

Различные шнурки для различных напряжений

Нагрузка может применяться во многих различных направлениях, причем каждая вызывает характерную реакцию напряжения на организме:

Для выполнения требований по точному измерению напряжений и деформаций в таких элементах были разработаны специальные модели тензодатчиков:

О линейных тензодатчиках | О тензодатчиках модели сдвига  | О схемах тройниковой розетки

Коэффициент Пуассона и анализ структурного напряжения:

                                                                                                              ,

Коэффициент Пуассона обычно составляет от 0,28 до 0,33 и имеет противоположный знак.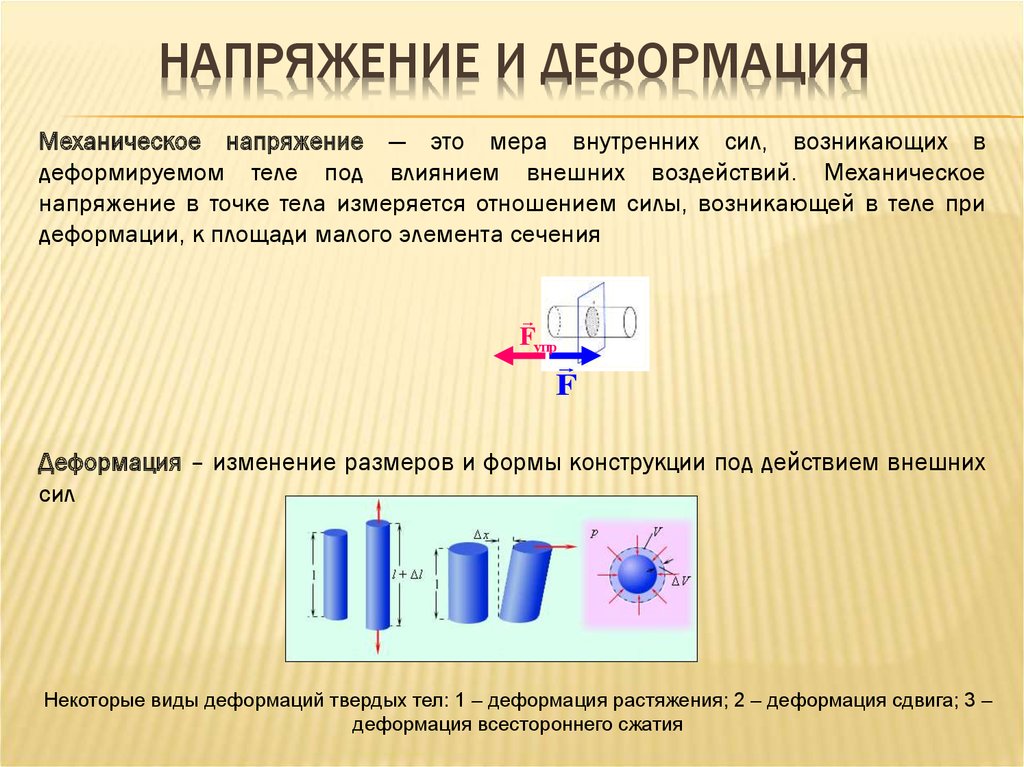

Как измерить деформацию, если ее направление неизвестно?

Измерение напряжения, когда деформация имеет известное направление (например, при изгибе балки), довольно прямолинейно:

Состояние одноосного напряжения будет рассчитываться непосредственно из показаний тензодатчика деформации, умноженной на модуль упругости

Но как измерить и рассчитать напряжение, если неизвестно направление главных деформаций?

Для этого можно использовать 3-элементную розетку:

Использование 3-элементной розетки позволит рассчитать основные деформации и правильно рассчитать основное напряжение, приложенное к детали:

Джайн -датчика и подключение к мосту Whetstone

С. в большинстве коммерчески доступных тензометрических приборов. Это в значительной степени связано с присущей ему способностью:

1. обнаруживать небольшие изменения сопротивления, возникающие в тензодатчике, поскольку он отслеживает даже незначительные изменения размеров на поверхности испытуемой детали под нагрузкой,

2. обеспечить нулевое выходное напряжение, когда испытуемая деталь находится в состоянии покоя, и

3. обеспечить компенсацию температурных изменений сопротивления в цепи тензорезистора.

В той или иной степени каждый из этих факторов важен для точных измерений тензодатчиков. В большинстве применений тензорезисторов для определения напряженного состояния поверхности испытуемой детали отдельные элементы тензорезисторов, независимо от того, являются ли они одноосными или розеточными, подключаются независимо к мосту Уитстона по схеме «четверть моста». Как обсуждалось

в следующих разделах схема подключения, выбранная для подключения тензорезистора к мостовой схеме, оказывает существенное влияние на точность измеренных данных о деформации.

Мост Уитстона

Схема моста Уитстона в простейшей форме (рис. 1) состоит из четырех резистивных элементов или плеч моста (R1, R2, R3, R4), соединенных в последовательно-параллельное расположение с источником напряжения возбуждения (Е). Точки соединения, образованные (соседними) парами плеч моста и подводящими проводами от источника напряжения возбуждения, являются входными углами моста; а те, которые образованы парами плеч моста и выводов измерения сигнала (эо), являются выходными углами. Для этого обсуждения стоит отметить, что каждый входной угол примыкает к каждому выходному углу, и каждое плечо моста соединено между двумя соседними углами.

Кроме того, если мостовая схема резистивно симметрична относительно воображаемой линии, проведенной через оба выходных угла, выходное напряжение eo будет равно нулю, независимо от уровня напряжения возбуждения, и мост будет «сбалансирован».

Руководство по выбору тензорезистора

Первым шагом в подготовке к установке любого тензорезистора является выбор тензорезистора, соответствующего задаче. На первый взгляд может показаться, что выбор калибра — простое упражнение, не имеющее большого значения для аналитика напряжения; но верно как раз обратное. Тщательный, рациональный выбор характеристик и параметров датчика может быть очень важным для: оптимизации работы датчика для определенных условий окружающей среды и условий эксплуатации, получения точных и надежных измерений деформации, облегчения установки и минимизации общей стоимости установки датчика. На монтажные и рабочие характеристики тензорезистора влияют следующие параметры, которые выбираются в разной степени:

• чувствительный к деформации сплав • материал подложки (основа) • сопротивление сетки • схема измерения • номер температурной компенсации • длина датчика • опции

В основном процесс выбора датчика состоит из определения конкретная доступная комбинация параметров, которая наиболее совместима с окружающей средой и другими условиями эксплуатации и в то же время наилучшим образом удовлетворяет ограничениям по установке и эксплуатации. Эти ограничения обычно выражаются в форме требований, таких как:

• точность • продолжительность испытания • стабильность • циклическая износостойкость • температура • простота установки • удлинение • окружающая среда важным экономическим показателем является общая стоимость всей установки, в которой стоимость манометра обычно составляет лишь небольшую часть. Во многих случаях выбор серии датчика или дополнительной функции

, которая увеличивает стоимость датчика, служит для снижения общей стоимости установки.

Несмотря на то, что существует несколько способов измерения деформации, наиболее распространенным является использование тензорезистора с присоединенным сопротивлением, устройства, электрическое сопротивление которого изменяется пропорционально величине деформации в устройстве.

В настоящее время наиболее широко используемым тензодатчиком является тензорезистор со связанным сопротивлением Advanced Sensors Technology.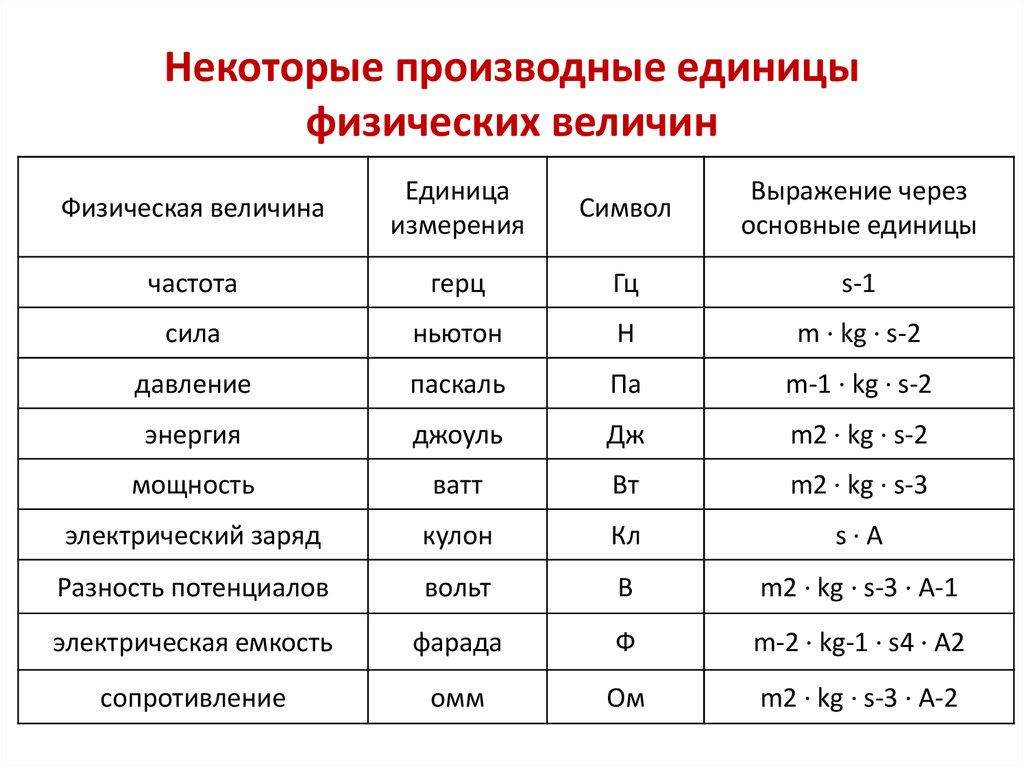 Компания Micro-Measurements использует точно изготовленную (собственно) металлическую фольгу для изготовления резистивного элемента, обеспечивая наилучшую консистенцию и доступное соответствие между тензорезисторами. Металлический тензорезистор состоит из металлической фольги, расположенной в виде сетки. Сетчатый рисунок максимизирует количество металлической фольги, подверженной деформации в параллельных направлениях.

СВЯЖИТЕСЬ С ЭКСПЕРТОМ ПО ТЕХНОЛОГИИ ТЕНЗОМЕТРИЧЕСКИХ ТЕХНОЛОГИЙ

Напряжение, деформация и модуль Юнга

Напряжение

Напряжение представляет собой отношение приложенной силы F к площади поперечного сечения — 5 определяется как 1 сила на единицу площади 9002 «.

• растягивающее напряжение — напряжение, стремящееся к растяжению или удлинению материала, — действует нормально к напряженной области
• сжимающее напряжение — напряжение, стремящееся сжать или укоротить материал — действует нормально к напряженной области
• напряжение сдвига — напряжение, стремящееся к сдвигу материала — действует в плоскости напряженной области под прямым углом к ​​сжимающему или растягивающему напряжению

растягивающее или сжимающее напряжение — нормальное напряжение

Плана обычно обозначается « Нормальное напряжение » или « прямое напряжение » и может быть выражен как

σ = F _N / A (1)

, где

σ = нормальное напряжение (PA (N /M ² ), PSI (LB _F /в ² )

F _{336). to the area (N, lb f )}

A = area (m ² , in ² )

• a kip is an imperial unit of force — it equals 1000 lb _f (фунт-сила)
• 1 килофунт = 4448,2216 ньютонов (Н) = 4,4482216 килоньютонов (кН)

Нормальная сила действует перпендикулярно площади и развивается всякий раз, когда внешние нагрузки имеют тенденцию толкать или тянуть два сегмента тела.

Пример. Сила растяжения, действующая на стержень

Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как

σ = (10 10 ³ Н)   / (π ((10 10 ^-3 M) / 2) ² )

= 1273888535 (N / M ² )

= 127 (MPA) 903

Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 в столбе из пихты Дугласа. Размер поста после обработки составляет 5,5 x 5,5 дюйма , а сжимающее напряжение можно рассчитать как

σ = (30000 фунтов)   / ((5,5 дюйма) (5,5 дюйма) ⁾

   = 991 (lb/in ² , psi)

Shear Stress

Stress parallel to a plane is usually denoted as » shear stress » and can be expressed as

τ = F _P /a (2)

, где

τ = напряжение сдвига (PA (N /M ² ), PSI (LB _{5 F ² ), PSI (LB 5 F /в ), PSI (LB 5 F /в ), PSI (LB 5 F /в ), PSI (LB 5 F 7). ))}

F _p = поперечная сила в плоскости площади (Н, фунт _f )

A = площадь (м ² , в ² , в ² ) в 900 усилие сдвига 1 900 плоскость области и развивается, когда внешние нагрузки имеют тенденцию заставлять два сегмента тела скользить друг по другу.

Деформация (деформация)

Деформация определяется как «деформация твердого тела под действием напряжения».

• Нормальная деформация — удлинение или сжатие сегмента линии
• деформация сдвига — изменение угла между двумя сегментами линии, первоначально перпендикулярно

Нормальный деформация и может быть выражен как

ε = DL / L _O

= σ / E (3) 9033

= σ / e (3) 33939393939393939393939393939393939393939393939393933

= σ / e (3) 9033

. где

dl = изменение длины (м, дюйм)

l _o = начальная длина (м, дюйм)0003

E = модуль Юнга (модуль упругости) (Па , (Н/м ² ), фунт/кв. дюйм (фунт _f /дюйм ² )) прогнозировать удлинение или сжатие объекта при воздействии силы

Обратите внимание, что деформация является безразмерной единицей, поскольку она представляет собой отношение двух длин. Но также общепринято указывать это как отношение двух единиц длины — например, м/м или дюйм/дюйм .

• Коэффициент Пуассона представляет собой отношение относительной деформации сжатия

Пример. Напряжение и изменение длины

Стержень в приведенном выше примере имеет длину 2 м и изготовлен из стали с модулем упругости 200 ГПа (200·10 ⁹ Н/м ² ) . Изменение длины можно рассчитать путем преобразования (3) в

dl = σ l _o  / E

     = (127 10 ⁶ PA) (2 м) / (200 10 ⁹ PA)

= 0,00127 M

= 1,27 мм

• Как рассчитать Radial Compractuctracture 3
  • Как рассчитать Radial Compractuctracture 999393099939303
  • .

  Энергия деформации

  Напряжение объекта сохраняет в нем энергию. Для осевой нагрузки накопленная энергия может быть выражена как

  U = 1/2 F _n dl

  , где

  U = энергия деформации (Дж (Н·м), фут-фунт)

  Модуль Юнга — модуль упругости (или модуль упругости) — закон Гука

  Большинство металлов деформируется пропорционально приложенной нагрузке в диапазоне нагрузок. Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .

  E = напряжение / деформация0301 = (F _N / A) / (DL / L _O ) (4)

  , где

  E = Модуль Янга (N / M ² ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in ) (LB / in )) 2 , psi)

  Модуль упругости или модуль Юнга обычно используется для металлов и металлических сплавов и выражается в единицах или Па . Модуль упругости при растяжении часто используется для пластмасс и выражается в терминах 10 ⁵ фунтов _f /in ² или ГПа .

  Модуль сдвига эластичности — или модуль жесткости

  g = напряжение / штамм

  = τ / γ
  

  9002 = (F 5. / F 5 (F 5 (A 5 (F 5 (A 5 333333335 (F 35 (F 35 (F 351 / P). / d)                                  (5)

  , где

  G = модуль упругости при сдвиге или модуль жесткости (Н/м ² ) (lb/in ² , psi)

  τ  = shear stress ((Pa) N/m ² , psi)

  γ = единица меньшей меры деформации сдвига
  

  F _P = силовая параллельна лицам, которые они действуют

  A = область (M ² ,

  A = область (м ² ,

  2 A = зона. с = смещение граней (м, дюйм)

  d = расстояние между смещенными поверхностями (м, дюймы)

  • Пластичные и хрупкие материалы

  Объемный модуль упругости равномерное сжатие. Объемный модуль упругости представляет собой отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.

  

  Модули упругости

  Модули упругости для некоторых распространенных материалов:

  Material	Young’s Modulus — E —	Shear Modulus — G —	Bulk Modulus — K —
  	(GPa) (10 6 psi)	(GPa) (10 6 psi)	(GPa) (10 6 psi)
  Aluminum	70	24	70
  Brass	91	36	61
  Copper	110	42	140
  Glass	55	23	37
  Iron	91	70	100
  Lead	16	5.