Содержание
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или
проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах
и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Внимание! Для работы калькулятора необходимо включить
поддержку JavaScript в вашем браузере!
Длина a
Длина b
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или
Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Смотрите также другие статьи
Технология соединения углов «теплый угол» — Статьи о строительстве деревянных домов и бань
Угловые соединения в деревянном доме – самые критичные места. Неправильно выполненные, они могут свести на нет пользу от толстого бруса, так как углы будут промерзать и сыреть. Исправить проблему потом, без каких-либо радикальных мер, увы, невозможно. Применение любых современных утеплителей, конечно, поможет устранить недостатки, однако испортит вид дома, и закроет вопрос с экологичностью и натуральностью деревянного строения.
При высыхании и усадке даже первоначально плотные узлы могут коробиться, рассыхаться, трескаться и деформироваться. Правильно скрепить брус, чтобы никакие факторы не могли нарушить плотность соединения, могут только опытные и добросовестные мастера.
Брус появился относительно недавно, веками проверенная технология сборки сруба применялась к бревнам. Однако с опытом строители разработали эффективные способы скрепления бруса по углам. Самой распространенной и надежной технологией считается «теплый угол».
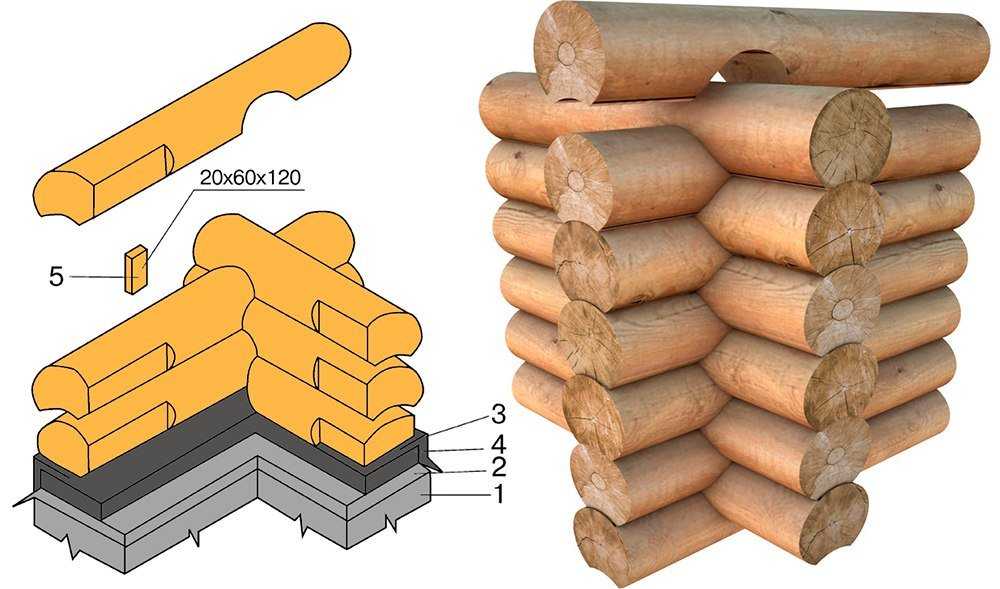
Суть метода сборки «теплый угол»
Соединение «теплый угол» – довольно сложное в технологическом плане. Суть способа примерна та же, что и при соединении профилированного бруса, однако в исполнении это соединение гораздо сложнее.
Главный принцип – сделать так, чтобы брусья глубоко проникали друг в друга. Обеспечивают такое проникновение разными методами, выбор которого зависит от предпочтений заказчика и опыта мастера.
- Брусья стыкуются концами, за границу угла не выступают.
- С остатком – брусья перекрещиваются и идут дальше (как бревна в классической избе).
- Встык – для крепления используют накладки и нагели.
- Т – образные, характерные для соединения наружных и внутренних стен.

Чтобы обеспечить качественное соединение в одном брусе выбирают пазы определенной формы, в другом – наоборот, оставляют шипы. Друг в друга они должны войти максимально плотно. Несколько проще в исполнении не шипы и пазы, а массивные вырезы, которые иногда делают на половину сечения бруса. Чтобы в этом случае обеспечить достаточную плотность соединения, используют нагели.
Способы соединения «теплый угол»
Способов выпиливания шипов и пазов довольно много, но все они являются разными вариантами нескольких основных принципов соединения.
Самое простое соединение – в прямой угол – чаще применяется для летних построек. У одного бруса под прямым или тупым углом выпиливается часть, а в другом делается соответствующая выемка. Этот способ обеспечивает достаточно прочное соединение. Важно соблюдать пропорции шипа и паза, чтобы чрезмерно не ослабить один из брусьев и не дать ему треснуть в наиболее тонком месте. При таком соединении каждый брус незначительно ослабляется, правильно выпилить пазы и шипы сможет даже неопытный мастер. Однако соединение может быть недостаточно плотным для постройки зимнего дома.
Однако соединение может быть недостаточно плотным для постройки зимнего дома.
Для повышения надежности и дополнительного обеспечения плотности соединения, применяют различные способы уплотнения, например, вставляют планки (вставные шипы), скрепляют нагелями.
Для зимних построек формы выпилов более сложные, их выполнение лучше доверять более опытным строителям. Чаще делают несколько пазов и шипов, чтобы обеспечить максимально плотное прилегание даже после усадки сруба. При этом только опытный мастер знает все пропорции, которые нужно соблюсти, чтобы брус не давал трещин, шипы не откалывались и соединение не деформировалось.
Все брусовые дома компании «Дачный участок» выполняются с применением «теплого угла». Пользуясь нашими услугами, можно быть уверенным в том, что все особенности технологи будут соблюдены, из углов не будет дуть, и их не нужно будет дополнительно утеплять.
Построение углов — Использование транспортира и циркуля, этапы построения, примеры
LearnPracticeDownload
Построение углов является одним из наиболее важных аспектов геометрии и представляет собой «чистую» форму геометрического построения. Термин «конструирование» в геометрии относится к точному рисованию форм, линий или углов с помощью математических инструментов. Для построения углов вам понадобится только циркуль или транспортир, линейка (прямая) и карандаш.
Термин «конструирование» в геометрии относится к точному рисованию форм, линий или углов с помощью математических инструментов. Для построения углов вам понадобится только циркуль или транспортир, линейка (прямая) и карандаш.
| 1. | Типы углов |
| 2. | Построение углов с помощью транспортира |
| 3. | Построение углов с помощью циркуля и линейки |
| 4. | Часто задаваемые вопросы по конструкции углов |
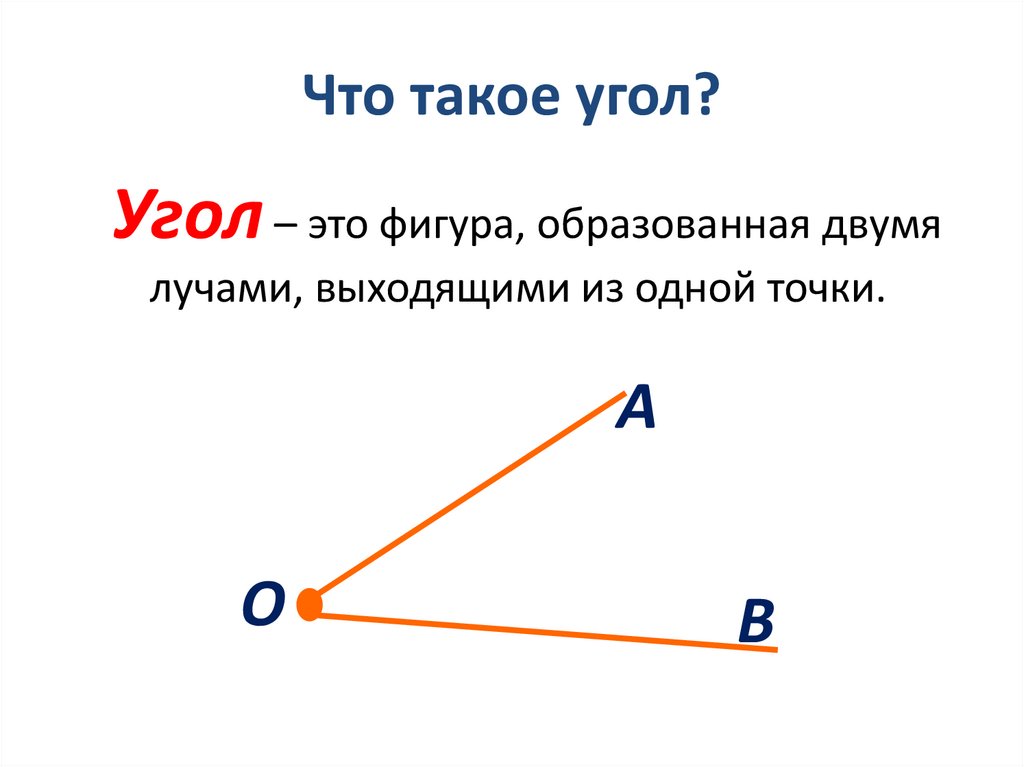
Типы углов
Когда две линии пересекаются и имеют общую конечную точку, то есть когда образуется угол. Изучение углов в геометрии очень важно. Ниже приведены 6 типов углов в геометрии, а также градусное измерение углов.
- Острый угол → Угол меньше 90° .
- Прямой угол → Угол, равный ровно 90°.

- Прямой угол → Угол, размер которого равен 180 градусам и выглядит как прямая линия.
- Тупой угол → Угол, размер которого больше 90°, но меньше 180°.
- Угол рефлекса → Угол, который всегда больше 180° (т. е. половина окружности), но меньше 360°.
- Полный угол поворота → угол, равный точно 360°.
Построение углов с помощью транспортира
Угол можно построить либо с помощью транспортира и линейки, либо с помощью циркуля и линейки. Давайте теперь посмотрим на шаги построения угла 50 ° с помощью транспортира.
- Шаг 1 — Нарисуйте отрезок OA.
- Шаг 2 — Поместите центр транспортира в точку O.
- Шаг 3 — Начиная с точки А по часовой стрелке и отметьте точку под углом 50 градусов, глядя на внешний круг транспортира. Обозначьте эту точку как B.
∠BOA — необходимый угол 50°.
Построение углов с помощью циркуля и линейки
Давайте научимся строить угол с помощью циркуля и линейки. В шагах, показанных ниже, мы построим угол 90°, а затем построим биссектрису угла, чтобы разделить пополам 9 градусов.0°, так что мы получим угол 45°.
- Шаг 1: Нарисуйте луч AB.
- Шаг 2: Используя A в качестве центра и любой ширины в качестве радиуса, нарисуйте дугу полукруга, которая касается отрезка AB, и обозначьте ее как Q.
- Шаг 3: Без изменения радиуса нарисуйте еще одну дугу с Q в центре и обозначьте эту точку как D.
- Шаг 4: Повторите тот же процесс с D в качестве центра и обозначьте нарисованную дугу буквой E.
- Шаг 5: Теперь с тем же радиусом и с E и D в качестве центров нарисуйте дуги, которые пересекаются друг с другом в точке, и обозначьте ее как F.
- Шаг 6: Теперь соедините точки A и F.
 Эта линия называется перпендикуляром и составляет 90 градусов с отрезком AB.
Эта линия называется перпендикуляром и составляет 90 градусов с отрезком AB. - Шаг 7: Обозначьте точку пересечения дуги полукруга с линией AF как P.
- Шаг 8: Теперь, используя тот же радиус, что и для дуги на шаге 2, нарисуйте две дуги с центрами P и Q. Обозначим точку пересечения этих дуг как R. Теперь соединим точки A и R. Теперь ∠RAB и ∠FAR равны 45° каждая.
Темы, связанные с построением углов
Ознакомьтесь с некоторыми интересными статьями, связанными с построением углов.
- Построение биссектрисы угла
- Геометрическая конструкция
- Пары уголков
- Биссектриса угла
- Уголки
Примеры построения углов
Пример 1: Постройте угол 75° с помощью циркуля и линейки.
Решение:
Шаг 1: Проведите луч AB. Используя A в качестве центра и любого радиуса, нарисуйте дугу, пересекающую AB в точке C.

Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, а D — в с центром и тем же радиусом, нарисуйте дугу, которая пересекает первую дугу в точке E
. Шаг 3: С точками E и D в качестве центров и с одинаковым радиусом мы рисуем две дуги, пересекающие друг друга в точке F. Соедините AF. Линия AF составляет 90° с отрезком AB.
Шаг 4: Отметьте точку, где линия AF касается дуги полукруга, как G. Теперь, используя G и D в качестве центров, нарисуйте две дуги, снова пересекающие друг друга в точке H. Теперь мы соединяем AH. ∠HAB= 75°.Конструкция уголка 75° показана ниже.
Пример 2: Как построить угол 105 градусов?
Решение:
Шаг 1: Проведите луч AB. Используя A в качестве центра и любую ширину в качестве радиуса, нарисуйте дугу, пересекающую AB в точке C.
Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, и, используя D в качестве центра и того же радиуса, рисуем другую дугу, снова пересекающую первую дугу в точке G.
Шаг 3: Используя D и G в качестве центров и с одинаковым радиусом, мы рисуем две дуги, пересекающие друг друга в точке F. Соединяем AF, который составляет 90°. Отметьте точку, где дуга полукруга пересекает линию AF, как E.
Шаг 4: С точками G и E в качестве центров и с одинаковым радиусом нарисуйте две дуги, пересекающие друг друга в точке H. Теперь соедините точки A и H.
∠НАВ = 105°.
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по построению углов
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по построению углов
Что такое построение углов?
Построение углов относится к построению различных углов, таких как 30°, 45°, 60°, 90°, с использованием циркуля, транспортира, линейки и карандаша. Это считается «чистой» формой геометрических построений.
Это считается «чистой» формой геометрических построений.
Как построить прямой угол?
Прямой угол – это угол, градусная мера которого равна 90 градусам. Чтобы построить прямой угол, выполните шаги, указанные ниже:
- Начертите отрезок AB и, используя A в качестве центра и произвольного радиуса, нарисуйте дугу так, чтобы она пересекала AB в точке C.
- Теперь, используя C в качестве центра и с тем же радиусом, что и в предыдущем шаге, нарисуйте дугу, пересекающую ранее нарисованную дугу в точке D.
- С D в центре и с тем же радиусом, нарисуйте дугу так, чтобы она пересекала дугу в точке E.
- С центрами D и E и одинаковым радиусом нарисуйте две дуги, пересекающиеся в точке F. Соедините F и A. Теперь ∠FAB — прямой угол, равный 90 градусам.
Как построить угол с помощью транспортира?
Любой угол от 0° до 180° можно легко построить с помощью транспортира. Например, мы можем построить угол 60 ° с помощью транспортира, выполнив шаги, указанные ниже.
- Нарисуем отрезок АВ любой подходящей длины.
- Теперь поместим транспортир на отрезок АВ.
- Затем поместим середину транспортира в точку А.
- На AB справа начнем отсчет с 0° против часовой стрелки и, наконец, отметим точку C, показывающую 60° на полукруглом ребре транспортира.
- Убираем транспортир и присоединяем АС.
- Получаем искомый угол ∠CAB = 60°.
Как построить биссектрису угла?
Биссектриса делит заданный угол на два равных угла. Чтобы построить биссектрису угла, выполните следующие шаги:
- Начертите заданный угол с помощью транспортира (скажем, 60°). Назовем вершины угла A, B и C так, что угол ABC = 60 градусов.
- С B в качестве центра и с более чем половиной BC в качестве радиуса нарисуйте дугу на обоих плечах, то есть AB и BC, и отметьте эти точки, где дуга касается сегментов линии, как D и E соответственно.
- Теперь, используя D и E в качестве центров, нарисуйте две дуги так, чтобы они пересекались в одной точке.
 Обозначьте эту точку как F.
Обозначьте эту точку как F. - Соедините F и B. FB — это биссектриса угла, и теперь ∠ABF и ∠FBC будут измерять по 30 градусов каждая.
.
Как измерять и строить углы?
Угол можно измерить с помощью транспортира, который представляет собой полукруглый диск, используемый для рисования и измерения углов. Большинство транспортиров измеряют углы в градусах и делятся на 180 равных частей. Их можно непосредственно использовать для измерения любого угла в диапазоне от 0° до 180° с помощью маркировки. Мы можем использовать либо транспортир, либо компас, чтобы построить углы определенного измерения.
Как строятся углы?
Чтобы построить угол любой степени, нам нужно использовать геометрический инструмент, называемый циркулем. После того, как луч нарисован, циркуль используется для обозначения дуг в соответствии с любым измеренным радиусом. Эти дуги пересекаются друг с другом в различных точках, образуя перпендикулярные линии, образующие угол. Для получения более подробных инструкций ознакомьтесь с разделом построения угла с помощью компаса и линейки в этой статье.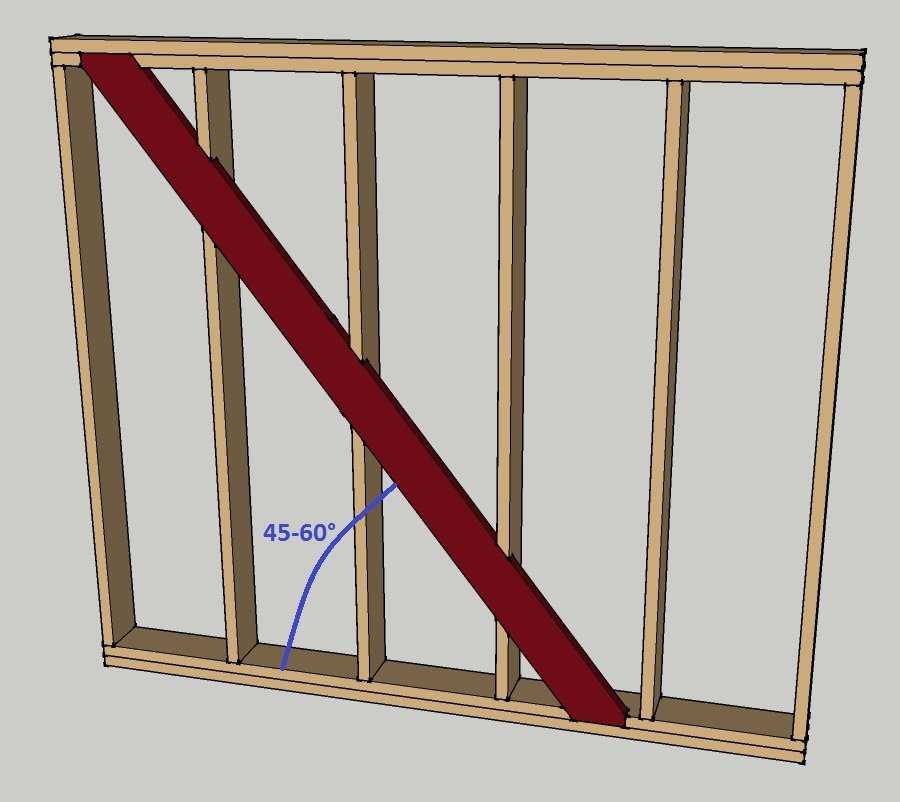
Как построить угол с помощью компаса?
Угол можно построить с помощью двух геометрических инструментов: циркуля и линейки. Вот шаги, чтобы построить угол с компасом:
- Нарисуйте любой отрезок AB.
- Удерживая острие компаса на A, нарисуйте дугу, пересекающую отрезок в точке S. Компас может быть любого измерения.
- Сохраняя те же размеры, заостренный конец помещается в точку S и пересекает первую дугу в точке R.
- Используя линейку, начертите линию, начинающуюся с точки A и соединяющую точку R, чтобы образовался угол.
- Используйте транспортир для измерения угла.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по углам
Рабочие листы по математике и наглядные пособия по
Построение углов 60, 120, 30 и 90
В этом разделе мы рассмотрим построение некоторых углов с
специальные размеры.
Построение угла 60°
Мы знаем, что все углы равностороннего треугольника равны 60°.
размер. Это говорит о том, что для построения угла 60 нам нужно
построить равносторонний треугольник, как описано ниже.
Шаг 1: Нарисуйте руку PQ .
Шаг 2: Поместите компас на P и нарисуйте дугу, проходящую через Q .
Шаг 3: Установите точку компаса на Q и начертите
дуга, проходящая через P . Пусть эта дуга перережет дугу, нарисованную в
Шаг 2 на R .
Построение угла 30°
Мы знаем, что:
Итак, чтобы построить угол 30, сначала постройте угол 60, а затем разделите его пополам. Часто мы применяем следующие шаги.
Шаг 1: Нарисуйте руку PQ .
Шаг 2: Поместите компас на P и нарисуйте дугу, проходящую через Q .
Шаг 3: Поместите точку компаса на Q и нарисуйте
дуга, которая пересекает дугу, нарисованную на шаге 2, по адресу R .
Шаг 4: С точкой компаса по-прежнему на Q , нарисуйте
дуга около T , как показано.
Шаг 5: Направив компас на R , нарисуйте дугу
, чтобы разрезать дугу, нарисованную на шаге 4, в точке T .
Шаг 6: Соедините T с P . Уголок QPT это 30.
Построение угла 120°
Мы знаем, что:
Это означает, что 120 является дополнением к 60. Следовательно, чтобы
построить угол 120°, построить угол 60°, а затем расширить один из его
руки, как показано ниже.
Построение угла 90°
Мы можем построить угол 90°, либо разделив прямой угол пополам, либо
используя следующие шаги.
Шаг 1: Нарисуйте руку PA .
Шаг 2: Поместите острие компаса в точке P и нарисуйте дугу, пересекающую руку в точке Q .
Шаг 3: Установите точку компаса на Q и начертите
дуга радиуса PQ , которая пересекает дугу, нарисованную на шаге 2 в точке Р .
Шаг 4: Направив компас на R , нарисуйте дугу
радиусом PQ , чтобы разрезать дугу, нарисованную на шаге 2 в точке S .
Шаг 5: Удерживая компас на отметке R , нарисуйте
другая дуга радиусом PQ около T , как показано.
Шаг 6: Направив компас на точку S , нарисуйте дугу
радиуса PQ , чтобы разрезать дугу, нарисованную на шаге 5 в точке T .
Шаг 7: Соедините T с P . Угол APT составляет
90.


 Эта линия называется перпендикуляром и составляет 90 градусов с отрезком AB.
Эта линия называется перпендикуляром и составляет 90 градусов с отрезком AB.

 Обозначьте эту точку как F.
Обозначьте эту точку как F.