Содержание
Технология соединения углов «теплый угол» — Статьи о строительстве деревянных домов и бань
Угловые соединения в деревянном доме – самые критичные места. Неправильно выполненные, они могут свести на нет пользу от толстого бруса, так как углы будут промерзать и сыреть. Исправить проблему потом, без каких-либо радикальных мер, увы, невозможно. Применение любых современных утеплителей, конечно, поможет устранить недостатки, однако испортит вид дома, и закроет вопрос с экологичностью и натуральностью деревянного строения.
При высыхании и усадке даже первоначально плотные узлы могут коробиться, рассыхаться, трескаться и деформироваться. Правильно скрепить брус, чтобы никакие факторы не могли нарушить плотность соединения, могут только опытные и добросовестные мастера.
Брус появился относительно недавно, веками проверенная технология сборки сруба применялась к бревнам. Однако с опытом строители разработали эффективные способы скрепления бруса по углам. Самой распространенной и надежной технологией считается «теплый угол».
Суть метода сборки «теплый угол»
Соединение «теплый угол» – довольно сложное в технологическом плане. Суть способа примерна та же, что и при соединении профилированного бруса, однако в исполнении это соединение гораздо сложнее.
Главный принцип – сделать так, чтобы брусья глубоко проникали друг в друга. Обеспечивают такое проникновение разными методами, выбор которого зависит от предпочтений заказчика и опыта мастера.
- Брусья стыкуются концами, за границу угла не выступают.
- С остатком – брусья перекрещиваются и идут дальше (как бревна в классической избе).
- Встык – для крепления используют накладки и нагели.
- Т – образные, характерные для соединения наружных и внутренних стен.
Чтобы обеспечить качественное соединение в одном брусе выбирают пазы определенной формы, в другом – наоборот, оставляют шипы. Друг в друга они должны войти максимально плотно. Несколько проще в исполнении не шипы и пазы, а массивные вырезы, которые иногда делают на половину сечения бруса. Чтобы в этом случае обеспечить достаточную плотность соединения, используют нагели.
Чтобы в этом случае обеспечить достаточную плотность соединения, используют нагели.
Способы соединения «теплый угол»
Способов выпиливания шипов и пазов довольно много, но все они являются разными вариантами нескольких основных принципов соединения.
Самое простое соединение – в прямой угол – чаще применяется для летних построек. У одного бруса под прямым или тупым углом выпиливается часть, а в другом делается соответствующая выемка. Этот способ обеспечивает достаточно прочное соединение. Важно соблюдать пропорции шипа и паза, чтобы чрезмерно не ослабить один из брусьев и не дать ему треснуть в наиболее тонком месте. При таком соединении каждый брус незначительно ослабляется, правильно выпилить пазы и шипы сможет даже неопытный мастер. Однако соединение может быть недостаточно плотным для постройки зимнего дома.
Для повышения надежности и дополнительного обеспечения плотности соединения, применяют различные способы уплотнения, например, вставляют планки (вставные шипы), скрепляют нагелями.
Для зимних построек формы выпилов более сложные, их выполнение лучше доверять более опытным строителям. Чаще делают несколько пазов и шипов, чтобы обеспечить максимально плотное прилегание даже после усадки сруба. При этом только опытный мастер знает все пропорции, которые нужно соблюсти, чтобы брус не давал трещин, шипы не откалывались и соединение не деформировалось.
Все брусовые дома компании «Дачный участок» выполняются с применением «теплого угла». Пользуясь нашими услугами, можно быть уверенным в том, что все особенности технологи будут соблюдены, из углов не будет дуть, и их не нужно будет дополнительно утеплять.
Теплый угол дома
Теплый угол — тип соединения бруса в коренной шип, который образует в срубе теплые непродуваемые углы. Он подразумевает соединение по методике “шип-паз”. В данном случае в одном брусе делают паз, а в другом — шип с размером под паз. При сборке сруба в паз укладывают межвенцовый утеплитель. Затем пиломатериалы плотно соединяют, а для прочности и надежности конструкции ряды чередуют пазами и шипами, забивают деревянными нагелями.
Рубка в теплый угол отличается эффективностью, надежностью, высокой теплоемкостью и долговечностью. В данном случае отсутствуют мостики холода, поэтому в помещении не будет сквозняков. Соединение “шип-паз” не требует дополнительных крепежей, поэтому монтаж пройдет легко и в короткие сроки. А сама конструкция теплого угла обеспечивает комфортную отделку внутри и снаружи дома, не требует особого декорирования. Брусовые стены выглядят органично и закончено.
Преимущества рубки в теплый угол
- Оперативная и легкая сборка сруба;
- Дополнительное утепление в углах дома;
- Высокая тепло- и звукоизоляция, отсутствие сквозняков, трещин и щелей, мостиков холода;
- Прочная и плотная сборка обеспечивает продолжительный срок службы сруба;
- Устойчивость к подвижкам грунта, перепадам температуры и сильным морозам;
- Внутрь дома не будет проникать сырость и влага, поэтому на стенах не появится плесень или грибок;
- Привлекательный внешний вид и внутри, и снаружи строения;
- Монтаж без дополнительных креплений — легкая в устройстве конструкция и минимальные расходы на строительство деревянного дома или бани.

Теплый угол для брусового дома
Рубка в теплый угол наиболее распространена при строительстве деревянных домов из профилированного бруса. Профилированный брус считается самым экологичным и качественным материалом из своей категории. Изделие изготавливают без применения токсичного клея, в отличие от клееного бруса. Материал и деревянные нагели сохраняют экологичность и натуральность строения.
Гладкие и ровные стороны обработанного бруса упрощают и ускоряют монтаж, позволяют легко подгонять и укладывать изделия максимально плотно. Это увеличивает тепло- и звукоизоляционные свойства сруба. За счет идеальных форм и равных параметров брус обеспечивает четкое вхождение элементов конструкции. Это создает монолитность и безупречную геометрию строения. Гарантирует надежность и долговечность сруба.
Профилированный брус выглядит эстетично и привлекательно. Брусовый дом гармонично впишется в загородный ландшафт, будет смотреться органично и оригинально. При этом изделие обязательно обрабатывают защитными средствами, чтобы предотвратить растрескивание и деформацию натурального материала, выцветание и потемнение, появление гнили и плесени, негативное влияние насекомых.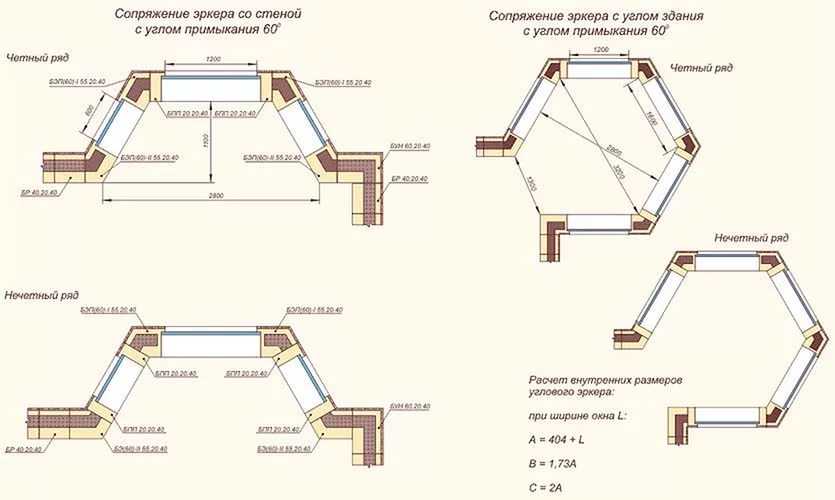
Фирма “МариСруб” строит деревянные дома из бруса от производителя. Мы самостоятельно отбираем и заготавливаем древесину, изготавливаем пиломатериалы. Это позволяет отслеживать каждый этап производства, экономить на доставке и услугах посредников. Поэтому у нас низкие цены на пиломатериалы!
Каждый брус или бревно проходит антисептирование и обработку антипиренами. Обязательно соблюдаем правила хранения и транспортировки материала, что увеличивает срок службы изделий. Предлагаем строительство деревянных домов “под ключ”, которое включает индивидуальное проектирование или доработку уже готового варианта, сборку и защитную обработку сруба, установку фундамента и кровли, подведение и подключение инженерных сетей, внешнюю и внутреннюю обработку дома. Гарантируем качество и оперативность работ!
Построение углов — Использование транспортира и циркуля, этапы построения, примеры
LearnPracticeDownload
Построение углов является одним из наиболее важных аспектов геометрии и представляет собой «чистую» форму геометрического построения. Термин «конструирование» в геометрии относится к точному рисованию форм, линий или углов с помощью математических инструментов. Для построения углов вам понадобится только циркуль или транспортир, линейка (прямая) и карандаш.
Термин «конструирование» в геометрии относится к точному рисованию форм, линий или углов с помощью математических инструментов. Для построения углов вам понадобится только циркуль или транспортир, линейка (прямая) и карандаш.
| 1. | Типы углов |
| 2. | Построение углов с помощью транспортира |
| 3. | Построение углов с помощью циркуля и линейки |
| 4. | Часто задаваемые вопросы по конструкции углов |
Типы углов
Когда две линии пересекаются и имеют общую конечную точку, то есть когда образуется угол. Изучение углов в геометрии очень важно. Ниже приведены 6 типов углов в геометрии, а также градусное измерение углов.
- Острый угол → Угол меньше 90° .
- Прямой угол → Угол, равный ровно 90°.

- Прямой угол → Угол, размер которого равен 180 градусам и выглядит как прямая линия.
- Тупой угол → Угол, размер которого больше 90°, но меньше 180°.
- Угол рефлекса → Угол, который всегда больше 180° (т. е. половина окружности), но меньше 360°.
- Полный угол поворота → угол, равный точно 360°.
Построение углов с помощью транспортира
Угол можно построить либо с помощью транспортира и линейки, либо с помощью циркуля и линейки. Давайте теперь посмотрим на шаги построения угла 50 ° с помощью транспортира.
- Шаг 1 — Нарисуйте отрезок OA.
- Шаг 2 — Поместите центр транспортира в точку O.
- Шаг 3 — Начиная с точки А по часовой стрелке и отметьте точку под углом 50 градусов, глядя на внешний круг транспортира. Обозначьте эту точку как B.
∠BOA — необходимый угол 50°.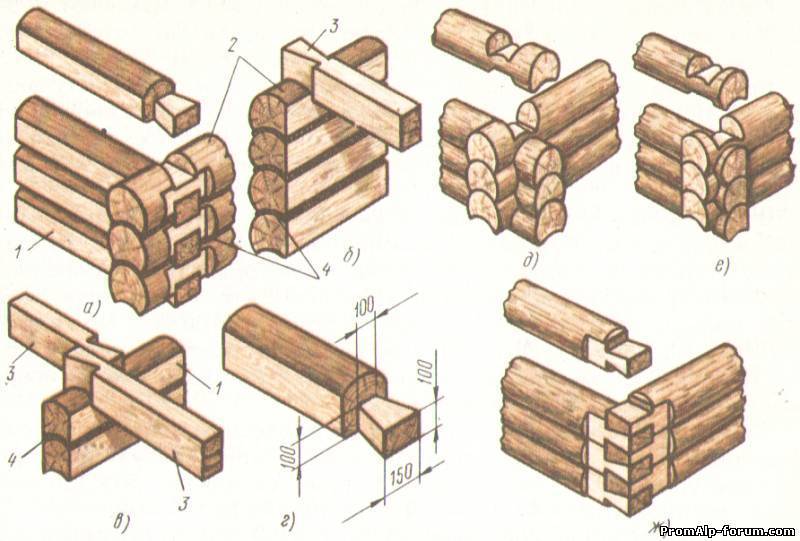
Построение углов с помощью циркуля и линейки
Давайте научимся строить угол с помощью циркуля и линейки. В шагах, показанных ниже, мы построим угол 90°, а затем построим биссектрису угла, чтобы разделить пополам 9 градусов.0°, так что мы получим угол 45°.
- Шаг 1: Нарисуйте луч AB.
- Шаг 2: Используя A в качестве центра и любой ширины в качестве радиуса, нарисуйте дугу полукруга, которая касается отрезка AB, и обозначьте ее как Q.
- Шаг 3: Без изменения радиуса нарисуйте еще одну дугу с Q в центре и обозначьте эту точку как D.
- Шаг 4: Повторите тот же процесс с D в качестве центра и обозначьте нарисованную дугу буквой E.
- Шаг 5: Теперь с тем же радиусом и с E и D в качестве центров нарисуйте дуги, которые пересекаются друг с другом в точке, и обозначьте ее как F.
- Шаг 6: Теперь соедините точки A и F.
 Эта линия называется перпендикулярной и составляет 90 градусов с отрезком AB.
Эта линия называется перпендикулярной и составляет 90 градусов с отрезком AB. - Шаг 7: Обозначьте точку пересечения дуги полукруга с линией AF как P.
- Шаг 8: Теперь, используя тот же радиус, что и для дуги на шаге 2, нарисуйте две дуги с центрами P и Q. Обозначим точку пересечения этих дуг как R. Теперь соединим точки A и R. Теперь ∠RAB и ∠FAR равны 45° каждая.
Темы, связанные с построением углов
Ознакомьтесь с некоторыми интересными статьями, связанными с построением углов.
- Построение биссектрисы угла
- Геометрическая конструкция
- Пары уголков
- Биссектриса угла
- Уголки
Примеры построения углов
Пример 1: Постройте угол 75° с помощью циркуля и линейки.
Решение:
Шаг 1: Проведите луч AB. Используя A в качестве центра и любого радиуса, нарисуйте дугу, пересекающую AB в точке C.

Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, а D — в с центром и тем же радиусом, нарисуйте дугу, которая пересекает первую дугу в точке E
. Шаг 3: С точками E и D в качестве центров и с одинаковым радиусом мы рисуем две дуги, пересекающие друг друга в точке F. Соедините AF. Линия AF составляет 90° с отрезком AB.
Шаг 4: Отметьте точку, где линия AF касается дуги полукруга, как G. Теперь, используя G и D в качестве центров, нарисуйте две дуги, снова пересекающие друг друга в точке H. Теперь мы соединяем AH. ∠HAB= 75°.Конструкция уголка 75° показана ниже.
Пример 2: Как построить угол 105 градусов?
Решение:
Шаг 1: Проведите луч AB. Используя A в качестве центра и любую ширину в качестве радиуса, нарисуйте дугу, пересекающую AB в точке C.
Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, и, используя D в качестве центра и того же радиуса, рисуем другую дугу, снова пересекающую первую дугу в точке G.
Шаг 3: Используя D и G в качестве центров и с одинаковым радиусом, мы рисуем две дуги, пересекающие друг друга в точке F. Соединяем AF, который составляет 90°. Отметьте точку, где дуга полукруга пересекает линию AF, как E.
Шаг 4: С точками G и E в качестве центров и с одинаковым радиусом нарисуйте две дуги, пересекающие друг друга в точке H. Теперь соедините точки A и H.
∠НАВ = 105°.
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по построению углов
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по построению углов
Что такое построение углов?
Построение углов относится к построению различных углов, таких как 30°, 45°, 60°, 90°, с использованием циркуля, транспортира, линейки и карандаша. Это считается «чистой» формой геометрических построений.
Это считается «чистой» формой геометрических построений.
Как построить прямой угол?
Прямой угол – это угол, градусная мера которого равна 90 градусам. Чтобы построить прямой угол, выполните шаги, указанные ниже:
- Начертите отрезок AB и, используя A в качестве центра и произвольного радиуса, нарисуйте дугу так, чтобы она пересекала AB в точке C.
- Теперь, используя C в качестве центра и с тем же радиусом, что и в предыдущем шаге, нарисуйте дугу, пересекающую ранее нарисованную дугу в точке D.
- С D в центре и с тем же радиусом, нарисуйте дугу так, чтобы она пересекала дугу в точке E.
- С центрами D и E и одинаковым радиусом нарисуйте две дуги, пересекающиеся в точке F. Соедините F и A. Теперь ∠FAB — прямой угол, равный 90 градусам.
Как построить угол с помощью транспортира?
Любой угол от 0° до 180° можно легко построить с помощью транспортира. Например, мы можем построить угол 60 ° с помощью транспортира, выполнив шаги, указанные ниже.
- Нарисуем отрезок АВ любой подходящей длины.
- Теперь поместим транспортир на отрезок АВ.
- Затем поместим середину транспортира в точку А.
- На AB справа начнем отсчет с 0° против часовой стрелки и, наконец, отметим точку C, показывающую 60° на полукруглом ребре транспортира.
- Убираем транспортир и присоединяем АС.
- Получаем искомый угол ∠CAB = 60°.
Как построить биссектрису угла?
Биссектриса делит заданный угол на два равных угла. Чтобы построить биссектрису угла, выполните следующие шаги:
- Начертите заданный угол с помощью транспортира (скажем, 60°). Назовем вершины угла A, B и C так, что угол ABC = 60 градусов.
- С B в качестве центра и с более чем половиной BC в качестве радиуса нарисуйте дугу на обоих плечах, то есть AB и BC, и отметьте эти точки, где дуга касается сегментов линии, как D и E соответственно.
- Теперь, используя D и E в качестве центров, нарисуйте две дуги так, чтобы они пересекались в одной точке.
 Обозначьте эту точку как F.
Обозначьте эту точку как F. - Соедините F и B. FB — это биссектриса угла, и теперь ∠ABF и ∠FBC будут измерять по 30 градусов каждая.
.
Как измерять и строить углы?
Угол можно измерить с помощью транспортира, который представляет собой полукруглый диск, используемый для рисования и измерения углов. Большинство транспортиров измеряют углы в градусах и делятся на 180 равных частей. Их можно непосредственно использовать для измерения любого угла в диапазоне от 0° до 180° с помощью маркировки. Мы можем использовать либо транспортир, либо компас, чтобы построить углы определенного измерения.
Как строятся углы?
Чтобы построить угол любой степени, нам нужно использовать геометрический инструмент, называемый циркулем. После того, как луч нарисован, циркуль используется для обозначения дуг в соответствии с любым измеренным радиусом. Эти дуги пересекаются друг с другом в различных точках, образуя перпендикулярные линии, образующие угол. Для получения более подробных инструкций ознакомьтесь с разделом построения угла с помощью компаса и линейки в этой статье.
Как построить угол с помощью компаса?
Угол можно построить с помощью двух геометрических инструментов: циркуля и линейки. Вот шаги, чтобы построить угол с компасом:
- Нарисуйте любой отрезок AB.
- Удерживая острие компаса на A, нарисуйте дугу, пересекающую отрезок в точке S. Компас может быть любого измерения.
- Сохраняя те же размеры, заостренный конец помещается в точку S и пересекает первую дугу в точке R.
- Используя линейку, начертите линию, начинающуюся с точки A и соединяющую точку R, чтобы образовался угол.
- Используйте транспортир для измерения угла.
Скачать бесплатные материалы для исследования
Рабочий лист углов
Математические листы и
Визуальная учебная программа
Строительство углов, строительство угла 90 градусов
СОДЕРЖАНИЕ
Этот пост также доступен: Угол — это форма, образованная двумя лучами, имеющими общую точку (называемую вершиной).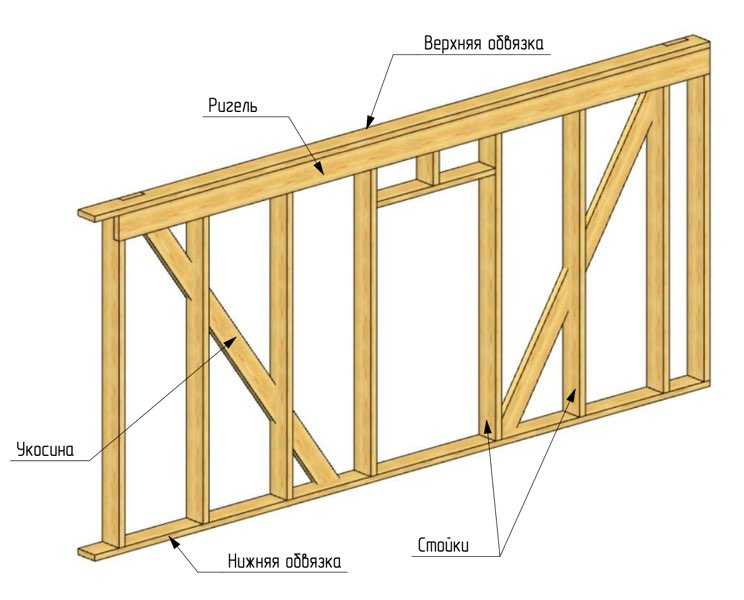 {\circ}$, $9{\circ}$ и т. д. с помощью циркуля и линейки (без использования транспортира).
{\circ}$, $9{\circ}$ и т. д. с помощью циркуля и линейки (без использования транспортира).
Давайте разберемся с процедурой построения углов.
Построение углов с помощью транспортира
С помощью транспортира можно построить угол любой величины.
Шаги построения углов с помощью транспортира следующие.
Шаг 1: Нарисуйте линию
Шаг 2: Отметьте на ней две точки $\text{A}$ и $\text{B}$.
Шаг 3: Поместите центр транспортира в точку $\text{A}$ так, чтобы отрезок $\text{AB}$ совпадал с линией транспортира.
Шаг 4: Начиная с $0$ (в транспортире) отметьте на бумаге точку $\text{C}$ под нужным углом.
Шаг 5: Соединить точки $\text{A}$ и $\text{C}$. $\angle \text{BAC}$ — искомый угол.
Шаг 6: Удлините отрезок $\text{AC}$ по мере необходимости. 9{\circ}$ и т. д.
Построение угла 60 градусов
Этапы построения угла 60 градусов:
Шаг 1: Нарисуйте отрезок. Отметьте левый конец как точку $\text{O}$, а правый конец как точку $\text{B}$.
Отметьте левый конец как точку $\text{O}$, а правый конец как точку $\text{B}$.
Шаг 2: Возьмите компас и откройте его на удобный радиус. Поместите его указатель на $\text{O}$ и кончиком карандаша проведите дугу, пересекающую линию $\text{OB}$, скажем, в $\text{P}$.
Шаг 3: 9{\circ}$.
Разделение угла пополам
Начнем с $\angle \text{AOB}$.
Шаги деления угла пополам:
Шаг 1: Возьмите циркуль и разверните его до удобного радиуса. С центром в $\text{O}$ проведите две дуги так, чтобы они пересекали лучи $\text{OA}$ и $\text{OB}$ в точках $\text{C}$ и $\text{ Д}$ соответственно.
Шаг 2: Не изменяя расстояния между сторонами компаса, нарисуйте две дуги с центрами $\text{C}$ и $\text{D}$ так, чтобы эти две дуги пересекались в точке, скажем $\текст{Е}$. 9{\circ}$ угол.
Шаг 1: Нарисуйте отрезок $\text{OA}$.
Шаг 2: Взять $\text{O}$ за центр и с помощью циркуля нарисовать дугу некоторого радиуса, которая пересекает $\text{OA}$ в точке $\text{B}$.
Шаг 3: Взяв $\text{B}$ за центр и с тем же радиусом, нарисуйте еще одну дугу, которая пересекает первую дугу в точке $\text{C}$.
Шаг 4: Взяв $\text{C}$ за центр и с тем же радиусом нарисуйте дугу, которая пересекает первую дугу в точке $\text{D}$. 9{\circ}$ угол.
Шаг 1: Нарисуйте отрезок $\text{AB}$ на плоском листе.
Шаг 2: С центром $\text{B}$ нарисуйте дугу, пересекающую $\text{AB}$ в точке $\text{C}$.
Шаг 3: Возьмем $\text{C}$ за центр и с таким же радиусом отметим на первой дуге две малые дуги $\text{D}$ и $\text{E}$.
Шаг 4: Возьмем $\text{D}$ и $\text{E}$ за центры и с одинаковым радиусом проведем две дуги, пересекающиеся в точке $\text{G}$. 9{\circ}$ и т. д. с помощью циркуля, транспортира, линейки и карандаша.
Что используется для изготовления уголков?
Мы можем использовать транспортир, чтобы построить угол в заданное количество градусов.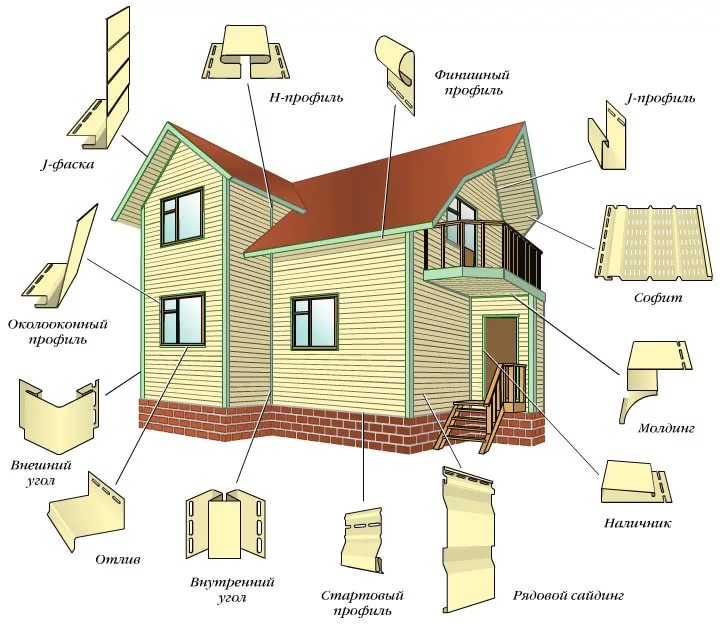 Мы также можем использовать линейку и циркуль, чтобы построить некоторые специальные углы.
Мы также можем использовать линейку и циркуль, чтобы построить некоторые специальные углы.
Какие две основные конструкции необходимы для построения угла с помощью линейки и циркуля?
Два основных построения с использованием циркуля и линейки:
а) построение угла 60 градусов
б) деление угла пополам
Заключение
Построение углов — одна из существенных частей геометрии. С помощью транспортира можно построить угол любого типа. Вы также можете построить определенные углы, используя линейку и циркуль.
Рекомендуемая литература
- Пара углов – определение, диаграммы, типы и примеры
- Типы углов в математике (острый, прямой, тупой, прямой и обратный)
- Что такое угол в геометрии – определение, свойства и Измерение
- Как построить касательную к окружности (с шагами и рисунками)
- Касательная к окружности — значение, свойства, примеры
- Углы в окружности — значение, свойства и примеры
- Хорда окружности — определение, свойства и примеры
- Как нарисовать круг (с шагами и рисунками)
- Что такое круг — части, свойства и примеры
- Как построить перпендикулярную линию (с шагами и примерами)
- Как построить параллельные линии (с помощью Шаги и примеры)
- Как построить отрезок (с шагами и примерами)
- Что такое коллинеарные точки в геометрии – определение, свойства и примеры
- Что такое поперечная линия в геометрии – определение, свойства и примеры
- Что такое параллельные линии в геометрии Геометрия – определение, свойства и примеры
- Что такое параллельные линии в геометрии – определение, условия и примеры
- Что такое полупрямая в геометрии – определение, свойства и примеры
- Что такое перпендикулярная линия в геометрии — определение, свойства и примеры
- Разница между аксиомой, постулатом и теоремой
- Линии в геометрии (определение, типы и примеры)
- Что такое двумерные фигуры — имена, определения и свойства
- 3D-фигуры – определение, свойства и типы
Вам также могут понравиться
Лучшие коробки для завтрака для учащихся
Содержание Критерии оценкиЛучшие ящики для завтрака для учащихся1.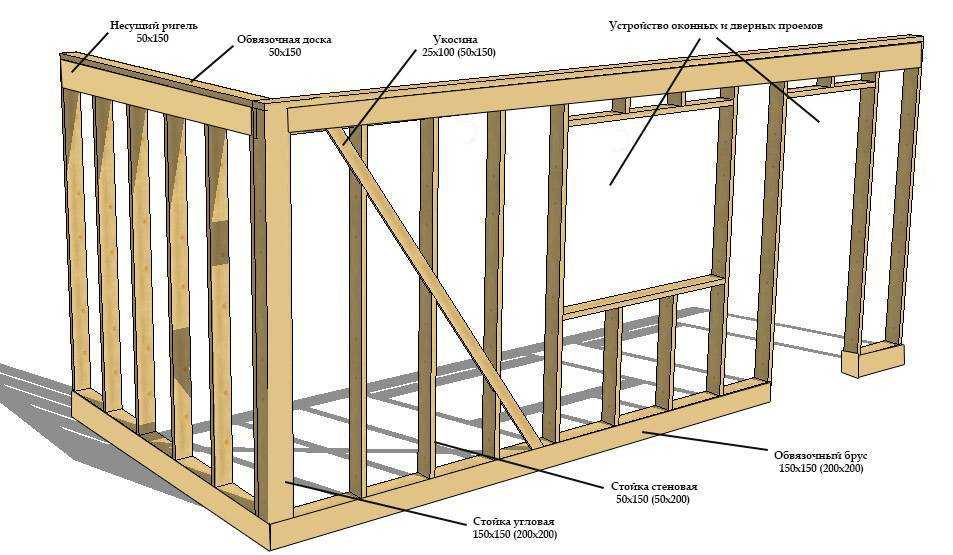



 Эта линия называется перпендикулярной и составляет 90 градусов с отрезком AB.
Эта линия называется перпендикулярной и составляет 90 градусов с отрезком AB.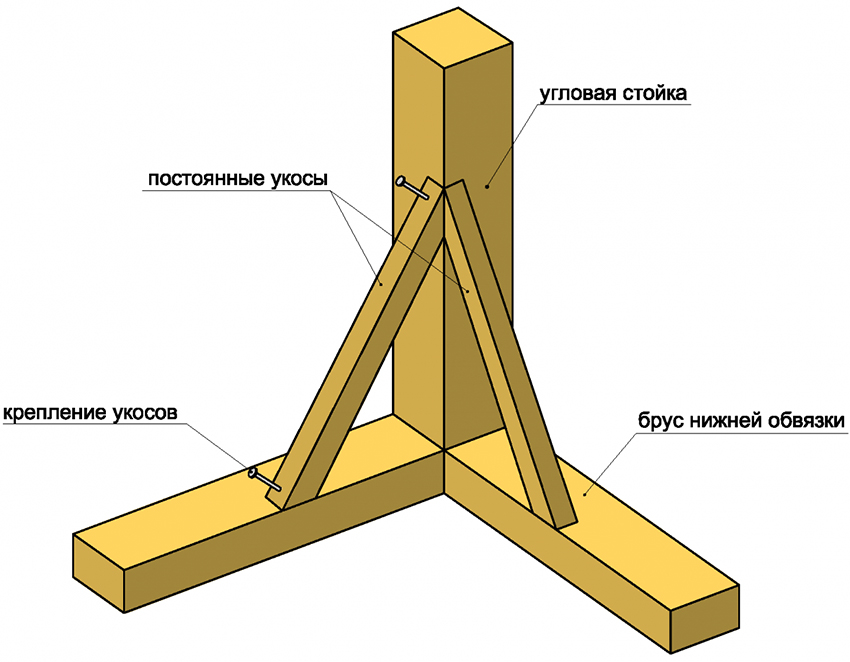

 Обозначьте эту точку как F.
Обозначьте эту точку как F.