Что такое общая плотность: Определение общей и моторной плотности урока | Методическая разработка по физкультуре по теме:

Определение общей и моторной плотности урока | Методическая разработка по физкультуре по теме:

Определение общей и моторной плотности урока.

Одним из показателей эффективности урока является его плотность. Чем рациональнее используется время на уроке, тем выше плотность. Плотность урока имеет существенное значение, поскольку она оказывает влияние на нагрузку, на выполнение поставленных перед уроком задач, на успешное выполнение учебной программы.

При подготовке к уроку учитель обязан продумать до мельчайших подробностей план проведения урока и решить, где должен быть просто показ упражнения, где подробное объяснение с показом, а где только распоряжение или команда.

Определять плотность урока необходимо в целом и по частям. Это обусловлено неодинаковыми возможностями и  условиями организации работы в подготовительной, основной и заключительной частях урока.  Точный учёт времени деятельности учителя и учеников на уроке определяется по скользящей стрелке секундомера. Секундомер пускается со звонком и останавливается после организованного выхода учащихся из класса. В качестве объекта наблюдения избирается так называемый средний ученик, достаточно активный и дисциплинированный.

Общая плотность урока – это отношение педагогически оправданных (рациональных) затрат времени к общей продолжительности урока.

                                    Время, педагогически оправданное *100%

Общая плотность =                         время урока

В числитель (педагогически оправданное время) входит выполнение физических упражнений, слушание, наблюдения, организация урока, словом всё то, без чего нельзя провести урок. Это время  умножается на 100% и делится на общее время урока. Общая плотность полноценного урока физической культуры должна приближаться 100%.

К снижению общей плотности урока приводят следующие причины: неоправданный отдых, опоздания на урок или преждевременное его окончание, выполнение упражнений с ошибками и не исправление их учителем, нарушение дисциплины и другое, чего не должно быть на уроке.

Моторная плотность урока – это отношение времени, использованного непосредственно на двигательную деятельность учащихся, к общей продолжительности урока.

        Для расчёта моторной плотности (МП) необходимо время выполнения физических упражнений умножить на 100% и разделить на общее время урока.

                                Время выполнения физических упражнений *100

Моторная плотность =                          время урока

Например, установлено, что суммарное время, затраченное учащимися на выполнение физических упражнений, равно 25 минут (оставшиеся 15 минут были затрачены на объяснение преподавателя, подготовку мест занятий, интервалы отдыха и т.п.)

В этом случае моторная плотность урока будет равна:

           25 минут*100%

МП=          40 мин.         =62,5%

Моторная плотность в процессе урока постоянно меняется. Изменения можно объяснить, прежде всего, различием содержания применяемых упражнений, местом их использования и методами их применения. Показатели моторной плотности меняются также и в зависимости то типа урока. Так, на уроках совершенствования техники движений и развития физических качеств оно может достигать 70 – 80%, а на уроках разучивания двигательных действий и формирования знаний, требующих значительных затрат времени на умственную деятельность занимающихся, моторная плотность может находиться на уровне 50%.        

Факторы, влияющие на моторную плотность:

1 Тип урока (начального разучивания, совершенствования)

2 Вид программы (гимнастика, лыжная подготовка, спортивные игры)

3 Количество и качество инвентаря

4 Количество учащихся в классе, их подготовленность

5 Мастерство педагога.

Пути повышения моторной плотности.

1 Использование безостановочных методов (поточный, круговой)

2 Заблаговременная подготовка инвентаря.

3 Увеличения количества отделений и групп

4 Хорошая дисциплина.

5 Использование временно освобождённых учеников.

6 Сочетание объяснения с показом (если это возможно) .

7 Введение дополнительных заданий во время ожидания.

8 Методические указания давать во время выполнения упражнений (если это возможно)

         При всей важности моторной плотности урока она не может достигать 100%, так как в противном случае не оставалось бы времени для объяснения материала, его осмысления учащимися, анализа ошибок, что неизбежно привело бы к снижению качества и эффективности учебной работы в целом. Хронометрия деятельности учащихся заносится в таблицу, производятся расчёты,  формируются выводы, и рекомендации.

    Хронометрия деятельности учащихся на уроке  физической культуры.   

Место проведения: спортивный зал.

Ведущий урока:

Класс: 3А

Время проведения: 40 мин. (8.00-8.40)

Задачи урока:

1.Совершенствование ловли и  передачи меча.

2. Развитие ловкости, быстроты двигательных реакций, общей выносливости. 3. Содействовать развитию психических процессов: внимания,          мышления.

4. Воспитывать смелость, выносливость.

1. ПОДГОТОВИТЕЛЬНАЯ ЧАСТЬ:

         ОП = 12. 0 : 12.0 * 100 = 720 :720 *100 = 100%

          МП = 11.3:12.0 * 100 = 678 : 720 * 100 =94.1%

   2. ОСНОВНАЯ ЧАСТЬ:

         ОП = (16.4+2.2+2.0):23.3 * 100 = (984+ 132+120):1398 * 100 =88.4

         МП = 16.4:23.3 * 100 = 984:1398 *100 = 70.3%

2. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ:

    ОП = 4.3 : 4.3 * 100 = 100 %

    МП = 3.0:4.3 * 100 = 180:258 * 100 = 69.7 %

ВСЕГО ЗА УРОК:  

  ОП = (31.3+4.5+2.0):40 *100 = (1878+270+120):2400 * 100 = 2268:2400      *100  = 94.5%

 МП = 31.3: 40 * 100 = 1866:2400 * 100 = 77.7%

ВЫВОДЫ И ПРЕДЛОЖЕНИЯ:

В подготовительной части урока общая и моторная плотность высокие, за счет применения безостановочных методов. Учащиеся хорошо подготовлены к предстоящей работе.

         В основной части урока общая, моторная плотность упала, за счет объяснения правил  игр.

         В заключительной части урока общая плотность отличная.

Рекомендуется предусмотреть задания для выбывших из игры: приседания, прыжки.

        В целом, плотность на уроке была достаточной.

            Оценка за урок: 5 «отлично»

Распономарёва Татьяна Валерьевна

Учитель физической культуры.

Школа №2

Красноярский край.

г. Лесосибирск

ОБЩАЯ И МОТОРНАЯ ПЛОТНОСТЬ ЗАНЯТИЯ

Различают общую и моторную плотность занятий физической культурой.

Целесообразность использования времени проведения занятия определяется по общей плотности занятия, которая выражена временным показателем ко всей длительности занятия, данного в процентах.

В моторную же плотность занятия входит только время, затраченное на выполнение физических упражнений, то есть непосредственная физическая нагрузка.

Общая плотность характеризуется отношением педагогически оправданного времени занятия (восприятие детьми объяснений, указаний, показа воспитателя, проделывание упражнений, наблюдение и анализ, установка и уборка пособий и т.д.) к продолжительности всего занятия.

Педагогически оправданным считается время, используемое на объяснение, указания для обеспечения точности выполнения, на показ, выполнение физических упражнений.

На необходимые вспомогательные действия в процессе занятия отводится минимальное время (раздача пособий, перестроение детей, перестановка физкультурных снарядов). Воспитатель заранее обдумывает организацию этих действий и исключает возможность непроизводительной затраты времени. Случайные организационные неполадки (отсутствие необходимых пособий для выполнения упражнений, недостатки в костюме или обуви детей, появление посторонних лиц в зале) определяются как педагогически неоправданная затрата времени.

Для характеристики физкультурного занятия очень важна моторная плотность — наибольшая двигательная деятельность детей в процессе занятия, что и определяет продуктивность каждого конкретного занятия. Однако требование к моторной плотности занятия не исключает осуществления учебно-воспитательных задач. Правильное целесообразное чередование умственной и физической деятельности детей необходимо и в учебно-воспитательных целях, являясь показателем продуманного содержания занятия, и его квалифицированного проведения.

Моторная плотность характеризует объем непосредственной двигательной деятельности ребенка на занятии. Она выражается отношением времени, затраченного на выполнение физических упражнений и игры, ко всей продолжительности занятия.

Чтобы правильно высчитать этот показатель, необходимо время, затраченное на выполнение движений, разделить на продолжительность занятия и умножить на 100.

Правильное целесообразное чередование умственной и физической деятельности детей является надежным показателем продуманного содержания занятия и его квалифицированного проведения.

Если общая плотность занятия, при правильной организации, приближается к 100 %, то моторная плотность может быть оценена только относительно педагогических задач занятия.

Наименьшая моторная плотность может быть при условии, если на занятии применяется 1/3 нового материала, тогда моторная плотность 65— 67 % считается нормой. Если же занятие решает задачи закрепления и совершенствования движений, то моторная плотность должна приближаться к 68—80%.

Эффективность проведения физкультурных занятий оценивается не только по успешному решению образовательных задач и влиянию на развитие личности, но и по оздоровительному воздействию на организм. Достаточная двигательная активность, с одной стороны, обеспечивает хорошее усвоение материала (при необходимом повторении материала) при разучивании, а с другой стороны, позволяет обеспечить тренирующее воздействие на организм ребенка.

Величина нагрузки и правильное ее распределение в течение занятия определяется по физиологической кривой, которая фиксирует работу сердечно-сосудистой системы при выполнении всех физических упражнений, включенных в разные части занятия.

По данным Г. П. Юрко, при правильном распределении нагрузки:

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Расчет
стоимостиГарантииОтзывы

— в вводной части занятия пульс должен повыситься на 15—20 % от исходного,

— увеличение пульса после выполнения общеразвивающих упражнений может составлять 40% от исходного;

— выполнение основных движений и проведение подвижной игры должны приводить к увеличению пульса на 70—80% от исходного,

— в заключительной части занятия оно увеличивается всего на 10—15% от исходного.

Спустя 3—4 мин после занятия пульс должен придти к исходному уровню.

Поможем написать любую работу на аналогичную
тему

• Реферат

  ОБЩАЯ И МОТОРНАЯ ПЛОТНОСТЬ ЗАНЯТИЯ

  От 250 руб

• Контрольная
  работа

  ОБЩАЯ И МОТОРНАЯ ПЛОТНОСТЬ ЗАНЯТИЯ

  От 250 руб

• Курсовая работа

  ОБЩАЯ И МОТОРНАЯ ПЛОТНОСТЬ ЗАНЯТИЯ

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

Расчет плотности

К концу этого урока вы сможете:

• вычислять одну переменную (плотность, массу или объем) из уравнения плотности
• рассчитать удельный вес объекта, а
• определяют, будет ли объект плавать или тонет, учитывая его плотность и плотность его окружения.

Введение в плотность

Плотность – это масса объекта, деленная на его объем.

Плотность часто выражается в граммах на кубический сантиметр (г/см ³ ). Помните, что граммы — это масса, а кубические сантиметры — это объем (тот же объем, что и 1 миллилитр).

Коробка с большим количеством частиц будет более плотной, чем такая же коробка с меньшим количеством частиц

Показать титры

Скрыть

от еинформрматики.

Плотность является фундаментальным понятием в науке; вы будете видеть это на протяжении всего обучения. Его довольно часто применяют при идентификации горных пород и минералов, так как плотность веществ редко изменяется существенно. Например, золото всегда будет иметь плотность 19..3 г/см ³ ; если минерал имеет другую плотность, это не золото.

Вероятно, вы интуитивно чувствуете плотность материалов, которые вы часто используете.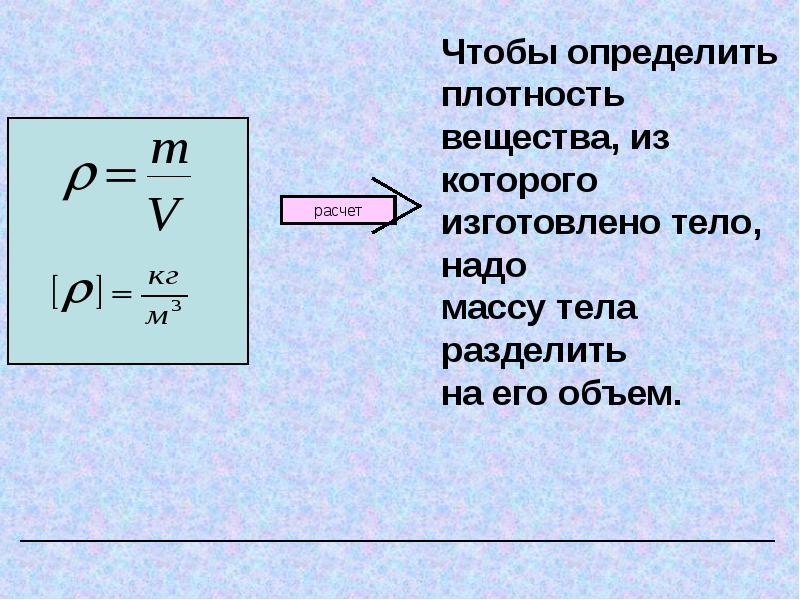 Например, губки имеют низкую плотность; они имеют низкую массу на единицу объема. Вы не удивитесь, когда большую губку легко поднять. Напротив, железо плотное. Если вы берете в руки железную сковороду, вы ожидаете, что она будет тяжелой.

Студенты и даже преподаватели часто путают массу и плотность. Слова тяжелый и легкий сами по себе относятся к массе, а не к плотности. Очень большая губка может много весить (иметь большую массу), но ее плотность мала, потому что весит она очень мало на единицу объема . Для плотности вам также необходимо учитывать размер или объем объекта.

Как определить плотность?

Бетонный куб будет весить больше, чем куб воздуха того же размера, потому что он более плотный

Показать кредиты

Скрыть

от Pitsco Lighter-Than-Air Flight

Плотность не измеряется напрямую. Обычно, если вы хотите узнать плотность чего-либо, вы должны взвесить это, а затем измерить объем.

Покажи мне, как это сделать

Скрыть

Вы собираете валун и возвращаете его в лабораторию, где вы взвешиваете его и находите, что его масса составляет 1000 г. Затем вы определяете объем 400 см ³ . Какова плотность вашего валуна?

Показать ответ

Скрыть

Плотность равна массе, деленной на объем,

В этом случае масса равна 1000 г, а объем равен 400 см ³ , поэтому вы делите 1000 г на 400 см ³ для получения 2,5 г/см ³ .

Еще одна хитрость, связанная с плотностью, заключается в том, что вы не можете добавлять плотности. Если у меня есть камень, состоящий из двух минералов, один с плотностью 2,8 г/см ³ , а другой с плотностью 3,5 г/см ³ , камень будет иметь плотность между 3,5 и 2,8 г/см ³ , а не плотностью 6,3 г/см ³ .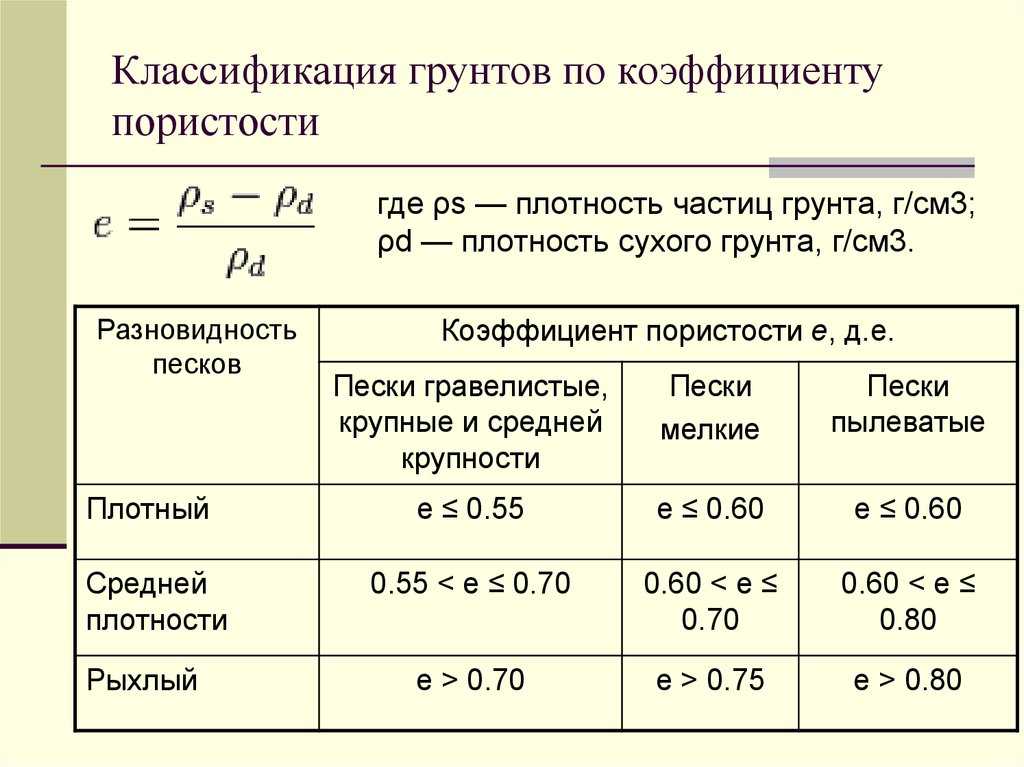 Это потому, что и будут добавлены к массе и объему двух минералов, и поэтому, когда они разделены, чтобы получить плотность, результат будет между ними.

Типичная плотность газов составляет порядка тысячных долей грамма на кубический сантиметр. Жидкости часто имеют плотность около 1,0 г/см ³ , и действительно, пресная вода имеет плотность 1,0 г/см ³ . Камни часто имеют плотность около 3 г/см ³ , а металлы часто имеют плотность выше 6 или 7 г/см ³ .

Как рассчитать удельный вес?

Чтобы рассчитать удельный вес (SG) объекта, вы сравниваете плотность объекта с плотностью воды:

Поскольку плотность воды в г/см ³ равна 1,0, SG объекта будет почти таким же, как его плотность в г/см ³ . Однако удельный вес является безразмерным числом и одинаков в метрической системе или любой другой системе измерения. Это очень полезно при сравнении плотности двух объектов. Поскольку удельный вес не имеет единиц измерения, не имеет значения, измерялась ли плотность в г/см ³ или в каких-то других единицах (например, в фунтах/футах ³ ).

Покажи мне, как это сделать

Скрыть

У вас есть образец базальта плотностью 210 фунтов/фут ³ . Плотность воды составляет 62,4 фунта/фут ³ . Каков удельный вес базальта?

Показать ответ

Скрыть

Удельный вес – это плотность вещества, деленная на плотность воды, поэтому

Итак, мы делим базальт (210 фунтов/фут ³ ) на плотность воды (62,4 lbs/ft ³ ), и получаем S.G.= 3,37 .

Зачем мне рассчитывать плотность или удельный вес?

Плотность имеет решающее значение для многих применений. Одним из наиболее важных является то, что плотность вещества определяет, будет ли оно плавать на другом. Менее плотные вещества будут плавать на более плотных (или подниматься сквозь них).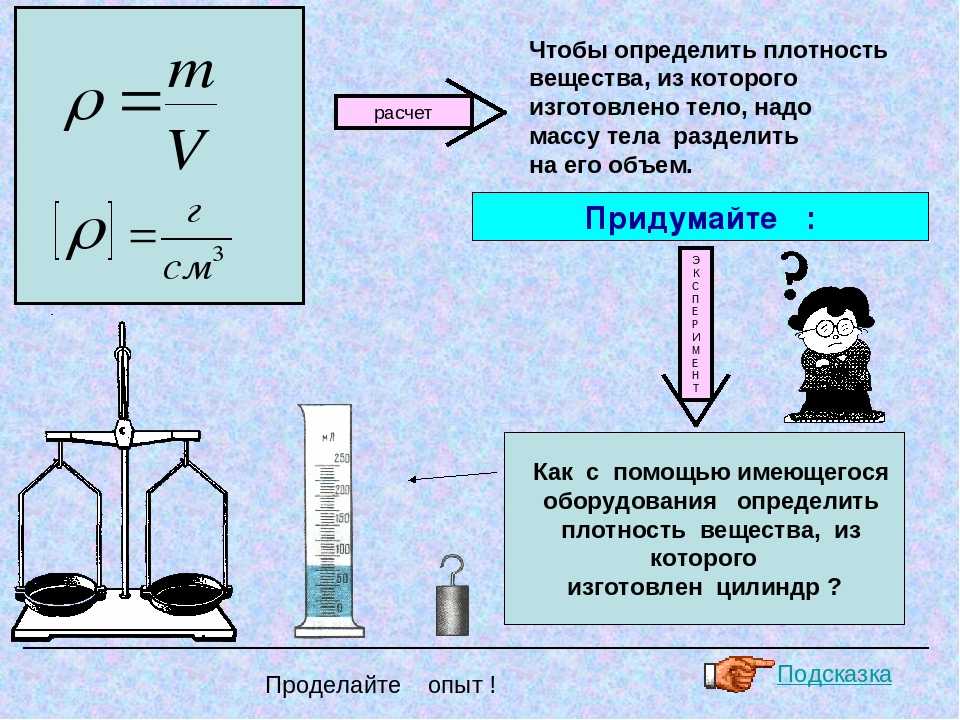 Вот несколько примеров того, как это объясняет повседневные явления:

Корабль, плывущий по воде, — отличная иллюстрация разницы между массой и плотностью. Корабль должен иметь плотность менее 1,0 г/см ³ (плотность воды), иначе она утонет. Корабли имеют большую массу, так как сделаны из стали, но поскольку имеют большой объем, их плотность меньше 1,0 г/см ³ . Если к ним добавить достаточно массы, чтобы их плотность превысила 1,0 г/см ³ , они утонут.

Чтобы попробовать несколько практических задач, перейдите на страницу примера задачи!

Где плотность используется в науках о Земле?

Галенит, свинцовая руда, является одним из самых плотных распространенных минералов.

Показать титры

Скрыть

с http://mineral.galleries.com/.

• Изостазия — определение высоты расположения континентов на мантии
• Тектоника плит — механизмы, приводящие в движение тектонику плит
• Минералы — определение названия минерала по его плотности
• Горные породы — определение названия и состава горной породы по ее плотности
• Гипсометрическая кривая — изучение причин изменения высоты на Земле
• Океанография — некоторые океанские течения и циркуляция океана контролируются плотностью

Следующие шаги

Я ГОТОВ К ПРАКТИКЕ!

Если вы считаете, что разобрались со всеми перечисленными выше вещами, нажмите на эту полосу, чтобы попробовать решить некоторые практические задачи с готовыми ответами!
Или, если вы хотите еще больше попрактиковаться, перейдите по ссылкам ниже

Дополнительная помощь по Density

Онлайн-лаборатория Einformatics по массе, объему и плотности создана Нью-Йоркским университетом. Он позволяет просматривать изображения измерений и вводить данные.

Гиперфизика в штате Джорджия имеет страницу о плотности и преобразователе плотности . Это включает в себя несколько связанных страниц, включая инструкции по измерению плотности с использованием принципа Архимеда.

На странице Википедии, посвященной удельной массе, объясняется, что такое удельная плотность и как она используется, и даже обсуждается ее использование в геонауках и минералогии. Однако содержание статей в Википедии может меняться, поэтому вам стоит быть осторожными.

На странице плотности Википедии есть общее обсуждение плотности и ее истории, расчетов и единиц измерения. Однако содержание статей в Википедии может меняться, поэтому вам стоит быть осторожными.

^{Эта страница была написана и составлена ​​доктором Эриком М. Баером, программа геологии, Общественный колледж Хайлайн, и доктором Дженнифер М. Веннер, факультет геологии, Университет Висконсина, Ошкош}

Lessoner. : Расчет плотности | Нагва

В этом объяснении мы узнаем, как использовать формулу
𝜌=𝑀𝑉 для расчета
плотности различных материалов и предметов.

Плотность — это свойство материалов и объектов, которое измеряет, сколько массы содержится в
заданное количество места.

Представьте себе две сферы одинакового размера: одна из железа, а другая из
полистирол. Интуитивно,
мы знаем, что железный шар будет намного тяжелее шара из полистирола.

Железная сфера будет иметь большую массу даже при том же размере, поэтому мы можем
говорят, что он имеет большую плотность.

Вот почему, например, железный шар утонет в луже воды, а полистироловый
мяч будет плавать.

Несмотря на то, что две сферы имеют одинаковый размер, железный шар имеет большую плотность
чем вода, а значит, он утонет. Однако полистирольная сфера имеет гораздо более низкую
плотность выше, чем у воды, поэтому она будет плавать.

Это будет иметь место независимо от того, насколько велики сферы. Это плотность,
определяет, плавают ли они, а не размер. Итак, если бы у нас была очень большая полистироловая сфера, она все равно
плавать в воде. Если бы у нас был очень маленький железный шар, он бы все равно утонул.

Плотность объекта обычно обозначается греческой буквой 𝜌 (которая имеет
имя «ро»). Эта буква выглядит как английская буква
𝑝, но если присмотреться, то видно, что он немного другой.

Мы определяем плотность 𝜌 объекта алгебраически как массу,
𝑀, деления объекта на его объем, 𝑉. В виде уравнения это выглядит так
𝜌=𝑀𝑉.

Определение: Плотность

Плотность — это мера массы на единицу объема объекта. Математическая формула для
плотность объекта, который обозначается 𝜌, равна
𝜌=𝑀𝑉,
где 𝑀 — масса объекта и
𝑉 — объем объекта.

Любой объект, сделанный исключительно из одного материала, будет иметь такую ​​же плотность, как и любой другой
объект, сделанный исключительно из
тот же материал. Например, кусок железа объемом
1 м ³ имеет точную
такой же плотности, как
блок железный объемом 100 м ³ . Массы и объемы двух блоков
очень разные, но
плотность блоков одинакова.

Это потому, что плотность блока — это отношение массы блока к
объем блока. В качестве
объем увеличивается, масса тоже, но соотношение этих двух
количества — плотность — остается неизменной.

Однако некоторые объекты состоят более чем из одного материала. Если каждый из этих
материалы имеют разный
плотность, то плотность всего объекта будет разной в разных частях
объекта.

Например, представьте себе сферу, сделанную частично из полистирола и частично из железа. Поперечное сечение
эта сфера показана на диаграмме ниже. Плотность в части шара из полистирола равна
много меньше, чем плотность части сферы, сделанной из железа.

Если 𝑀 — масса всей сферы и 𝑉
объем всей сферы, то 𝜌=𝑀𝑉 даст
средняя плотность шара. Эта плотность будет иметь значение, равное
между плотностью полистирола и плотностью железа.

Важно помнить об этой разнице. Для конкретного материала плотность
этот материал является собственностью
которую можно найти, и любой объект, сделанный исключительно из этого материала, будет иметь это
плотность.

Однако плотность объекта, состоящего из нескольких материалов, зависит от
этот объект. Мы можем использовать
𝜌=𝑀𝑉, где 𝑀 — масса
весь объект, а 𝑉 — объем всего объекта, чтобы найти
средняя плотность всего объекта.

Пример 1. Определение плотности объекта по его массе и объему

Куб имеет массу
30 кг. Если объем куба
0,02 м ³ ,
какова его плотность?

Ответ

Плотность объекта определяется выражением 𝜌=𝑀𝑉,
где 𝑀 – масса
объект, а 𝑉 — объем объекта.

В этом вопросе нам говорят, что масса куба равна
𝑀=30кг и объем
куб это
𝑉=0,02м.

Нам нужно подставить известные нам значения массы и объема куба
в уравнение
для плотности. Это дает нам
𝜌=𝑀𝑉=300.02.kgm

Разобьем эту дробь на числовую часть и часть единиц. Мы можем рассчитать числовое значение
часть как 300,02=1500. Единицы в дроби можно просто оставить как
килограмм на кубический метр.

В итоге наш окончательный ответ:
𝜌=1500.kgm

Если нам нужно вычислить плотность куба, мы можем это сделать, если знаем массу
куба и длину одной из его сторон.

Напомним, что объем куба со стороной 𝑙 определяется выражением
𝑉=𝑙.

Давайте рассмотрим несколько примеров использования формулы плотности.

Пример 2. Определение плотности объекта по его массе и размерам

Небольшой железный куб имеет длину стороны
0,15 м. Если масса куба
26,6 кг, что это такое
плотность? Дайте ответ ближайшему
килограмм на кубический метр.

Ответ

В этом вопросе нам дана масса,
𝑀=26,6 кг, железного куба, а также
его боковая длина,
𝑙=0,15м.

Учитывая это, нас просят найти плотность 𝜌 куба. Напомним, что
формула плотности
𝜌=𝑀𝑉.

Мы знаем массу куба, но не знаем объем куба. Мы можем отработать
объема по формуле объема куба, которая
𝑉=𝑙. Итак, здесь у нас есть
𝑉=(15)=0,15=0,003375.ммм

Теперь мы можем определить плотность железного куба. Нам нужно заменить
масса 𝑀=26,6 кг и объем
𝑉=0,003375m в наше уравнение плотности. Это дает
𝜌=𝑀𝑉=26.60.003375.kgm

Теперь мы можем упростить этот результат, вычислив сначала числовое значение
26,60,003375=7881,48148. Мы можем оставить единицы как есть, т.е.
килограмм на кубический метр. Это означает
𝜌=7881,48148.кгм

Вопрос просит нас дать наш ответ ближайшему
килограмм на кубический метр, что означает, что наш окончательный ответ
𝜌=7881. kgm

Пример 3. Нахождение объема объекта по его массе и плотности

Найдите объем алюминиевого блока массой 54 кг. Используйте значение 2‎ ‎700 кг/м ³
для плотности алюминия.

Ответ

В этом вопросе нам дают плотность блока алюминия и просят
найти объем
блокировать. Нам говорят, что блок имеет массу, которую мы назовем 𝑀, равной
54 кг. Нам также сообщают, что
плотность алюминия, из которого сделан блок, составляет
𝜌=2700/кгм.

Мы можем изменить нашу формулу плотности, 𝜌=𝑀𝑉,
и использовать его для расчета объема этого блока. Если мы
умножаем обе части уравнения плотности на объем 𝑉, получаем
𝑉𝜌=𝑀.

Затем мы можем разделить обе части уравнения на плотность 𝜌, что дает нам
𝑉=𝑀𝜌.

Теперь нам нужно подставить известные нам значения для 𝑀 и
𝜌 в это уравнение. Это дает нам
𝑉=542700.kgkgm

Разобьем эту дробь на числовую часть и единицы. Мы можем вычислить числовую часть
быть 542700=0,02.

Для единиц мы можем сначала разделить верх и низ дроби на
килограммов, и мы видим, что все
кг вычесть из дроби. Во-вторых,
если мы умножим верх и низ дроби на
кубометры,
видим, что m ³ отменяется снизу,
но у нас есть коэффициент m ³ сверху. Это означает, что
в общем у нас
𝑉=0.02.m

Таким образом, наш окончательный ответ состоит в том, что объем алюминиевого блока равен
0,02 м ³ .

Пример 4. Определение массы объекта по его объему и плотности

Выяснено, что корона из цельного золота имеет объем
150 см ³ . Найдите массу золотой короны,
используя значение
19‎ ‎300 кг/м ³ для плотности золота. Дайте ответ с точностью до одного десятичного знака.

Ответ

В этом вопросе нам дан объем 𝑉 и плотность
𝜌 золотой короны и являются
попросили найти массу 𝑀 короны.

Давайте начнем с нашего уравнения для плотности,
𝜌=𝑀𝑉, и умножьте обе части на объем, 𝑉, чтобы получить
𝑀=𝜌𝑉.

Это говорит нам о том, что масса кроны — это просто плотность кроны, умноженная на объем
короны.

Однако, прежде чем мы вычислим массу, мы должны заметить, что плотность
корона дана нам
в килограммах на кубический метр,
тогда как объем короны дан нам в
кубических сантиметров.

Это означает, что прежде чем мы начнем объединять эти две величины, нам нужно
преобразовать их в
сопоставимые единицы. Здесь это означает, что мы должны преобразовать объем в
кубических метров.

Напомним, что 100=1см. Это означает, что
(100)=1см, и, таким образом,
1000000=1см.

Это означает, что нам нужно разделить объем на
кубических сантиметров на
1‎ ‎000‎ ‎000. Громкость
короны, в кубических метрах, тогда
𝑉=0,00015. м

Теперь мы можем заменить известные нам значения 𝜌 и
𝑉 найти массу
корона быть
𝑀=19300×0,00015=(19300×0,00015)×=2,895.kgmmkgmmkg

Вопрос требует, чтобы наш ответ давался с точностью до одного десятичного знака, поэтому
наш окончательный ответ для массы
корона 2,9 кг.

Обратите внимание, что в этом вопросе нам не нужно было знать точную форму
корона. Пока мы
сообщив его объем, мы можем использовать уравнение для плотности, чтобы найти его массу.

Мы можем рассчитать плотность сферического объекта, если знаем массу шара,
𝑀 и радиус сферы 𝑟. Зная эти величины, мы можем использовать
уравнение для плотности, которое
𝜌=𝑀𝑉,
вместе с уравнением объема шара, которое
𝑉=43𝜋𝑟.

Если мы объединим эти два уравнения, подставив выражение для объема
сферу в
уравнение для плотности, то мы видим, что плотность сферы определяется выражением
𝜌=𝑀𝜋𝑟. 

Если мы умножим верхнюю и нижнюю части дроби на 3, мы получим
𝜌=3𝑀4𝜋𝑟,
потому что множители 3 сокращаются в нижней части дроби.

Пример 5. Определение плотности сферы по ее массе и радиусу

Шар для боулинга имеет массу 5,5 кг. Шар для боулинга представляет собой шар радиусом
7 см. Что это
плотность шара для боулинга? Дайте ответ ближайшему
килограмм на кубический метр.

Ответ

В этом вопросе нам предлагается вычислить плотность 𝜌 сферического
объект с учетом его массы и радиуса.

Здесь масса шара для боулинга равна
𝑀=5,5 кг и радиус
шар для боулинга 𝑟=7см. Примечание
что вопрос просит нас дать плотность в килограммах на кубический метр, так что это будет полезно для нас
перевести радиус, данный нам в сантиметрах, в
метров, прежде чем мы начнем.

Это делается путем деления радиуса в сантиметрах на 100,
поэтому 𝑟=0,07 м.

Поскольку теперь мы знаем всю необходимую информацию, мы можем использовать уравнение для плотности сферы,
который
𝜌=3𝑀4𝜋𝑟.

Нам просто нужно подставить значения для 𝑀 и 𝑟 для этого вопроса. Если мы сделаем это,
мы нашли
𝜌=3×(5,5)4𝜋×(0,07).kgm

Если мы решим это, не забывая возводить в куб и число, и единицы в
знаменатель, находим
𝜌=3828.07….kgm

Нас просят передать наш ответ ближайшему
килограмм на кубический метр,
так что наш окончательный ответ просто
𝜌=3828.кгм

Пример 6. Определение объема объекта по его массе и плотности

Стальной шарикоподшипник имеет массу 0,034 г. Найдите диаметр шарикоподшипника в
миллиметры,
округляется до ближайшего миллиметра. Используйте значение
8‎ ‎000 кг/м ³
для плотности стали.

Ответ

В этом примере нам дана масса
𝑀=0,034 г сферического шара
подшипник, а также его плотность,
𝜌=8000/кгм. Учитывая это, нас просят найти диаметр шарикоподшипника.

Назовем диаметр шарикоподшипника 𝑑 и вспомним, что диаметр в два раза больше радиуса. Итак, если радиус шарикоподшипника равен 𝑟, то
𝑑=2𝑟. Имея это в виду, давайте сначала вычислим радиус
шарикоподшипника, используя уравнение плотности для сферы.

Давайте начнем с изменения уравнения плотности для сферы, чтобы мы могли его использовать
найти радиус 𝑟. Плотность сферы определяется выражением
𝜌=3𝑀4𝜋𝑟.

Сначала умножим обе части этого уравнения на 𝑟. Это дает нам
𝜌𝑟=3𝑀4𝜋.

Мы можем разделить обе части на 𝜌, чтобы получить
𝑟=3𝑀4𝜋𝜌.

Теперь правая часть этого уравнения включает только члены, которые мы знаем
ценность.

Единственным дополнительным шагом здесь является преобразование массы шарикоподшипника, который
дается нам в граммах, в
килограммы. Мы хотим сделать это, потому что плотность стали дана нам в единицах
килограмм на кубический метр.

Мы делаем это, уменьшая массу в граммах на 1‎ ‎000, поэтому масса шарикоподшипника равна
𝑀=0,000034.кг

С этим номером будет намного проще работать, если мы напишем его научным языком.
обозначение. Это дает нам
𝑀=3,4×10кг.

Мы можем подставить значения 𝑀 и
𝜌 что мы должны сейчас получить
𝑟=3×3,4×104𝜋(8000/).кгкгм

Обратите внимание, что единицы
кг отменить, и вообще,
единицы становятся m ³ . Мы также можем вычислить числовую часть этой дроби как
3×3,4×104×8000=1,0146×10,

Это означает, что мы нашли значение радиуса в кубе равным
𝑟=1,0146×10,m

Теперь нам нужно извлечь кубический корень из этого выражения, чтобы найти радиус
шариковый подшипник, который дает
𝑟=0,001004847…,м
где мы взяли кубический корень единиц, а также числа. Вопрос
просит нас дать
наш ответ в миллиметрах,
поэтому давайте преобразуем наш ответ (в метрах)
в миллиметры. Это делается путем умножения
на 1‎ ‎000, и так
𝑟=1,004847….мм

Нам нужно удвоить радиус 𝑟, чтобы найти диаметр 𝑑 шарикоподшипника,
как задается вопрос. Это, до ближайшего
миллиметр, дает
𝑑=2𝑟=2,мм

Это наш окончательный ответ: диаметр шарикоподшипника
2 мм.

Мы также можем захотеть рассчитать плотность объекта с менее правильными размерами,
например, прямоугольная призма длиной 𝑙, шириной
𝑤 и высота ℎ.

В этом случае объем 𝑉 прямоугольной призмы равен
𝑉=𝑙𝑤ℎ.

Это означает, что, объединив эту формулу объема с нашим уравнением для плотности
объекта, мы можем
говорят, что плотность прямоугольной призмы материала равна
𝜌=𝑀𝑉=𝑀𝑙𝑤ℎ.

Пример 7. Определение плотности объекта по его массе и размерам

Кирпич имеет массу 3,5 кг. Представляет собой прямоугольную призму со сторонами
23 см,
11 см и
7 см. Какова плотность кирпича? Дайте ответ ближайшему
килограмм на кубический метр.

Ответ

В этом вопросе нам даны размеры и масса прямоугольной призмы и
просят найти его плотность.

Неважно, какое из измерений мы называем длиной, высотой или шириной. Для этого примера давайте
говорят, что длина — это самое длинное измерение, поэтому
𝑙=23см. Скажем так
ширина — средняя длина,
значит 𝑤=11см. Окончательно,
скажем, что высота является наименьшей длиной, поэтому
ℎ=7см.

Обратите внимание, что все эти расстояния указаны в
сантиметров, но мы
просят рассчитать плотность в килограммах на кубический метр. Проще будет перевести расстояния в метры
прежде чем мы приступим к расчету
плотность. Это делается путем деления каждого расстояния на
сантиметров на 100,
и так, размеры кирпича можно записать как
𝑙=0,23,𝑤=0,11,ℎ=0,07.ммм

Это означает, что мы готовы рассчитать плотность кирпича. Мы используем эти размеры вместе с
масса кирпича, о которой нам говорят в вопросе, равна
3,5 кг. Это позволяет нам вычислить
𝜌=𝑀𝑙𝑤ℎ=3,5(0,23)(0,11)(0,07).кгммм

Мы можем сначала упростить блоки, которые становятся
килограмм на кубический метр, а затем рассчитать числовое значение, которое будет
3,5(0,23)×(0,11)×(0,07)=1976,28….

Это означает, что плотность кирпича с точностью до килограмма на кубический метр составляет
𝜌=1976,кгм
и это наш окончательный ответ.

Ключевые моменты

• Плотность — это свойство материалов, которое измеряет массу на единицу объема
  материал, который может быть записан как
  𝜌=𝑀𝑉,
  где 𝜌 — плотность массы, 𝑀 — масса материала,
  𝑉 — объем материала.
• Для данного материала его плотность всегда одинакова
  независимо от формы предмета, изготовленного из этого материала.
• Мы можем объединить уравнение для плотности с уравнением для объема для
  определенные формы предметов. В частности, для куба с длиной стороны
  𝑙, его объем 𝑉=𝑙.