Содержание
Модуль упругости бетона: таблица, как определить
Выбор стройматериала является важнейшей задачей строителя перед началом выполнения работ. Модуль упругости бетона — один из главных критериев, влияющих на эксплуатационные характеристики. Параметр определяет возможность стеснения и расширения материала, зависит от многих факторов, которые важно учитывать.
Содержание
- Что за величина?
- Разновидности бетона и их показатель упругости
- Таблица, содержащая классы и соответствующие модули упругости
- От чего зависит величина?
- Как определить?
Что за величина?
Модуль упругости бетона — это возможность конструкции противостоять изменениям под воздействиями внешних факторов. Это важный критерий выбора марки материала для определенной работы, так как затвердевший материал в процессе эксплуатации сжимается и растягивается. Поэтому на этапе проектирования нужно правильно рассчитать допустимые значения для той или иной конструкции.
Для расчетов пользуются таблицами определения модуля упругости, что представлены в нормативах для строительных работ.
Разновидности бетона и их показатель упругости
Бетонный камень в окончательном виде — твердый материал, что под влиянием внешней среды способен деформироваться. При постоянных механических нагрузках, даже модуль упругости железобетона может быть недостаточно высоким. Для определения вида прочности учитывается 2 критерия — растяжение и сжатие, что влияют на сопротивление нагрузкам.
Различают следующие виды материала:
Материал может производиться в нескольких разновидностях.
- тяжелые;
- легкие;
- мелкозернистые;
- поризованные;
- автоклавного твердения.
Таблица, содержащая классы и соответствующие модули упругости
Классификация в таблице производится согласно СП 52—101—2003:
| Класс бетона | Модуль упругости |
| 19,0 | В10 |
| 24,0 | В15 |
| 27,5 | В20 |
| 30,0 | В25 |
| 32,5 | В30 |
| 34,5 | В35 |
| 36,0 | В40 |
| 37,0 | В45 |
| 38,0 | В50 |
| 39,0 | В55 |
| 39,5 | В60 |
От чего зависит величина?
На величину данного показателя значительно влияет наполнитель в материала.
Упругость раствора зависит от множества факторов. Первое, на что обращают внимание — наполнитель. Коэффициент напрямую связан с упругостью раствора. Так, высокими показателями являются тяжелые бетоны, наполнителями в которых являются гравий и щебень. Допустимые нагрузки на постройки из такого материала самые высокие, поэтому важно выбирать правильные заполнители. Учитывают не только интенсивность нагрузок, но и частоту.
Возраст и время укладки материала играют немаловажную роль в показателях модуля упругости. Крепость материала возрастает на протяжении 50 лет с момента заливки, вне зависимости от внешних температур (до 230 ⁰C). Кроме того, характеристики завися от процесса затвердевания (автоклавный, естественный). Чтобы узнать продолжительность предполагаемых нагрузок, нужно начальный показатель перемножать с показателем: 0,7 для поризованных бетонов, 0,85 — для тяжелых легких и мелкозернистых.
Возраст залитого материала находится в прямопропорциональной зависимости с данным показателем.
Классы бетонного раствора в частной стройке варьируют в пределах В7,5—30 (марки М100—400), но таких прочностных и других характеристик хватает вне зависимости от требований и сложностей конструкций. Показатели модуля увеличивает арматура, так как характеристики арматуры повышают показатели общей конструкции. Методика укладки арматуры в бетон определяется ГОСТом 24452—80.
Посмотреть «ГОСТ 24452-80» или cкачать в PDF (350 KB)
Как определить?
СП 52 101 2003 — стандарт определения параметров применения бетона. Здесь указаны значения всех необходимых коэффициентов для расчета параметров, а подтверждение проводится путем эксперимента на изготовленных образцах. Суть испытания заключается в постепенной нагрузке на образцы (цилиндры или призмы из бетонной смеси) путем осевого сжимающего нагружения до разрушения. Параллельно измеряется степень деформации.
Посмотреть «СП 52-101-2003» или cкачать в PDF (1007.4 KB)
Результаты можно обозначить следующим образом:
- Показатель соответствует расчетам, образец поддался пластической деформации без растрескивания.
- Предварительные подсчеты неверные: при предполагаемом нагружении образец подвергается сильным разрушениям.
Расчетным способом определяют запас прочности не только обычных зданий, но и арочных сооружений, перекрытий, мостов и дорог. Модуль упругости асфальтобетона при использовании — проблемная задача проектирования, так как подход, разрешающий провести точные расчеты еще не выведен. Не удается определить взаимосвязь между статическим и динамическим модулями в процессе использования дорог.
Модуль упругости бетона
СП 63.13330.2012
6.1.15 Значения начального модуля упругости бетона при сжатии и растяжении принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 6.11. Значения модуля сдвига бетона принимают равным 0,4Еb.
При продолжительном действии нагрузки значения модуля деформаций бетона определяют по формуле:
где φb,cr— коэффициент ползучести бетона, принимаемый согласно 6.1.16.
Таблица 6.11
| Бетон | Значения начального модуля упругости бетона при сжатии и растяжении Eb, МПа × 10-3, при классе бетона по прочности на сжатие | |||||||||||||||||||||
| В1,5 | В2 | В2,5 | В3,5 | В5 | В7,5 | в10 | В12,5 | B15 | B20 | B25 | в30 | В35 | В40 | В45 | В50 | В55 | В60 | В70 | В80 | В90 | В100 | |
| Тяжелый | — | — | — | 9,5 | 13,0 | 16,0 | 19,0 | 21,5 | 24,0 | 27,5 | 30,0 | 32,5 | 34,5 | 36,0 | 37,0 | 38,0 | 39,0 | 39,5 | 41,0 | 42,0 | 42,5 | 43 |
| Мелкозернистый групп: | ||||||||||||||||||||||
| А — естественного твердения | — | — | — | 7,0 | 10 | 13,5 | 15,5 | 17,5 | 19,5 | 22,0 | 24,0 | 26,0 | 27,5 | 28,5 | — | — | — | — | — | — | — | — |
| Б — автоклавного твердения | — | — | — | — | — | — | — | — | 16,5 | 18,0 | 19,5 | 21,0 | 22,0 | 23,0 | 23,5 | 24,0 | 24,5 | 25,0 | — | — | — | — |
| Легкий и порисованный марки по средней плотности: | ||||||||||||||||||||||
| D800 | — | — | 4,0 | 4,5 | 5,0 | 5,5 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1000 | — | — | 5,0 | 5,5 | 6,3 | 7,2 | 8,0 | 8,4 | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1200 | — | — | 6,0 | 6,7 | 7,6 | 8,7 | 9,5 | 10,0 | 10,5 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1400 | — | — | 7,0 | 7,8 | 8,8 | 10,0 | 11,0 | 11,7 | 12,5 | 13,5 | 14,5 | 15,5 | — | — | — | — | — | — | — | — | — | — |
| D1600 | — | — | — | 9,0 | 10,0 | 11,5 | 12,5 | 13,2 | 14,0 | 15,5 | 16,5 | 17,5 | 18,0 | — | — | — | — | — | — | — | — | — |
| D1800 | — | — | — | — | 11,2 | 13,0 | 14,0 | 14,7 | 15,5 | 17,0 | 18,5 | 19,5 | 20,5 | 21,0 | — | — | — | — | — | — | — | — |
| D2000 | — | — | — | — | — | 14,5 | 16,0 | 17,0 | 18,0 | 19,5 | 21,0 | 22,0 | 23,0 | 23,5 | — | — | — | — | — | — | — | — |
| Ячеистый автоклавного твердения марки по средней плотности: | ||||||||||||||||||||||
| D500 | 1,4 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D600 | 1,7 | 1,8 | 2,1 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D700 | 1,9 | 2,2 | 2,5 | 2,9 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D800 | — | — | 2,9 | 3,4 | 4,0 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D900 | — | — | — | 3,8 | 4,5 | 5,5 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1000 | — | — | — | — | 5,0 | 6,0 | 7,0 | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1100 | — | — | — | — | — | 6,8 | 7,9 | 8,3 | 8,6 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| D1200 | — | — | — | — | — | — | 8,4 | 8,8 | 9,3 | — | — | — | — | — | — | — | — | — | — | — | — | — |
| Примечания 1 Для мелкозернистого бетона группы А, подвергнутого тепловой обработке или при атмосферном давлении, значения начальных модулей упругости бетона следует принимать с коэффициентом 0,89. 2 Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции. 3 Для ячеистого бетона неавтоклавного твердения значения Еbпринимают как для бетона автоклавного твердения с умножением на коэффициент 0,8. 4 Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент α = 0,56 + 0,006 В. | ||||||||||||||||||||||
6.1.16 Значения коэффициента ползучести бетона φb,cr принимают в зависимости от условий окружающей среды (относительной влажности воздуха) и класса бетона. Значения коэффициентов ползучести тяжелого, мелкозернистого и напрягающего бетонов приведены в таблице 6.12.
Значения коэффициента ползучести легких, ячеистых и поризованных бетонов следует принимать по специальным указаниям.
Допускается принимать значения коэффициента ползучести легких бетонов по таблице 6.
12 с понижающим коэффициентом (ρ/2200)2.
Таблица 6.12
| Относительная влажность воздуха окружающей среды, % | Значения коэффициента ползучести бетона φb,crпри классе тяжелого бетона на сжатие | ||||||||||
| В10 | В15 | В20 | В25 | взо | В35 | В40 | В45 | В50 | В55 | В60 — В100 | |
| Выше 75 | 2,8 | 2,4 | 2,0 | 1,8 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,1 | 1,0 |
| 40 — 75 | 3,9 | 3,4 | 2,8 | 2,5 | 2,3 | 2,1 | 1,9 | 1,8 | 1,6 | 1,5 | 1,4 |
| Ниже 40 | 5,6 | 4,8 | 4,0 | 3,6 | 3,2 | 3,0 | 2,8 | 2,6 | 2,4 | 2,2 | 2,0 |
Примечание — Относительную влажность воздуха окружающей среды принимают по СП 131.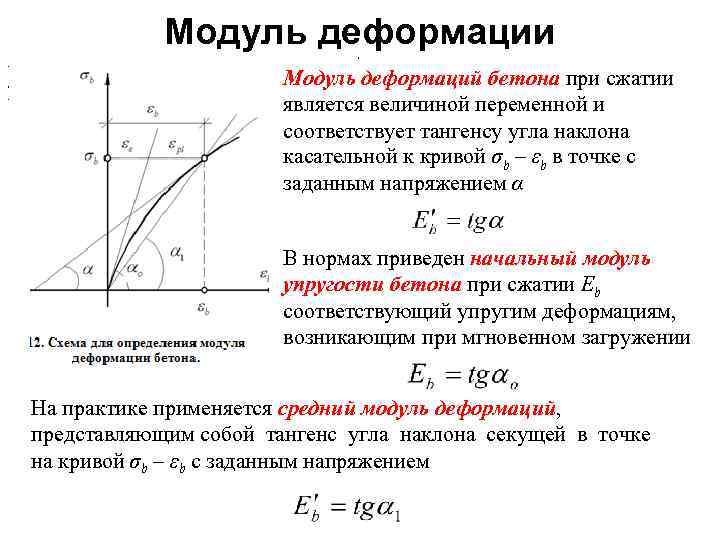 13330 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. | |||||||||||
python — Разница между модулем (%) и делением пола (//) в NumPy?
спросил
Изменено
4 месяца назад
Просмотрено
13 тысяч раз
Недавно я прочитал книгу о Numpy, в которой упоминаются различные типы ufuncs, где я столкнулся с двумя разными ufuncs, а именно «модуль», обозначаемый % символ и ‘подразделение этажа’ // . Может ли кто-нибудь объяснить разницу между ними и почему два оператора предназначены для выполнения одного и того же (по-моему, отображать напоминание о делении)? Пожалуйста, поправьте, если я ошибаюсь.
- питон
- numpy
- целочисленное деление
3
Обе являются действительными математическими функциями с разными результатами.
модуль
Функция модуля вычисляет остаток от деления, который является «остатком» целочисленного деления.
этаж
Функция этажа обеспечивает нижнюю границу целочисленного деления. Верхняя граница вычисляется функцией ceil. (По сути, функция пола отсекает все десятичные знаки).
а=5 б=2 print(a%b) # Печатает 1 как остаток print(a//b) # Печатает 2, так как 5/2=2.5 и десятичная дробь обрезана print(a - (a//b)*b) # Выводит 1, это модуль, вычисленный функцией floor
Предположим, что a = 10, b = 6
a%b даст вам остаток, то есть 4
a//b даст вам частное, то есть 1
Соотношение между делением пола и модулем может быть полезно для понимания этого:
знаменатель = 6 # заменить на любое целое число numerator = 10 # заменить на любое целое число floor_division_result = числитель//знаменатель modulo_result = числитель% знаменатель # это утверждение всегда будет истинным: утверждать знаменатель * floor_division_result + modulo_result == числитель
Один из способов понять разницу между модулем и делением пола — использовать аналогию с циферблатом часов.
Представьте себе стрелку на этих часах. Он перемещается и указывает на число. Допустим, цикл начинается (и заканчивается), когда стрелка указывает на 12. В этом контексте
- модуль, %, это то место, куда прямо сейчас указывает стрелка
- деление пола — это количество раз, когда стрелка завершила цикл
.
Пример 1
В первом цикле, когда стрелка указывает на 4, модуль равен 4, но деление пола равно 0,
4 % 12 # возвращает 4 4 // 12 # возвращает 0
Пример 2
Во втором цикле, когда стрелка указывает на 4, модуль по-прежнему равен 4, но деление пола теперь равно 1
16 % 12 # возвращает 4 16 // 12 # возвращает 1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
python, как получить усеченный по модулю против напольного по модулю
Я получаю Усеченное деление по сравнению с напольным делением в Python можно использовать следующим образом
>>> -1 / 2
-0,5
>>> -1 // 2
-1
, но есть ли эквивалент по модулю?
например, когда дивиденд отрицательный
для
−9 mod 4.
Ясно, что мы имеем
−9 = 4 * (−2) − 1
и
−9 = 4 * (−3) + 3.mod 4 = 3
усеченный по модулю подразумевает, что -9 mod 4 = -1
для оператора по модулю python, по умолчанию используется версия % с полом
-61 % 60 = 59
есть ли встроенная/библиотекарная поддержка, аналогичная делению по модулю на усеченное или напольное деление, или мне нужно использовать собственное?
речь идет об усеченном и напольном модуле, а не о делении. 20оба%20%20делитель%20и%20дивиденд%20являются%20отрицательными, деление%20возвращает%20%20отрицательное%20остаток.
- питон
- по модулю
0
Есть math.remainder :
>>> импортировать математику >>> math.остаток(-9, 4) -1,0 >>> int(math.remainder(-9, 4)) -1 >>> -9 % 4 3
Итак, после некоторых исследований метод по модулю по умолчанию зависит от языка, для python
8 % -3 = -1
например для javascript
8 % -3 = 2
это потому, что для js используется метод trunc
r = a - (n * trunc(a/n))
р - остаток.
